表面有螺旋装饰条的大跨贝壳形屋盖风荷载特性

2021-06-06林拥军林池锬刘开齐

西南交通大学学报 2021年2期

林拥军，林池锬，周祎，刘开齐，潘毅

（1. 西南交通大学土木工程学院，四川成都 610031；2. 南充市审计局，四川南充 637003）

大跨屋盖结构具有柔性大、阻尼小、自振频率低等特点，对风荷载十分敏感[1-3]. 其中，大跨贝壳形屋盖结构因造型独特、体型复杂，风荷载在屋面的流动分离作用十分复杂. 但是，已有文献和现行规范[4]并没有类似外形的体型系数可供参考. 同时，为彰显建筑物的艺术表现力，屋盖表面往往需要设置肋条、波纹等复杂的建筑装饰构件[5]. 在装饰构件尺寸日趋大型化、布置形式复杂多变的情况下，屋盖特征湍流以及风荷载的作用机理与普通大跨贝壳形屋盖有很大的不同[6].

目前，在建筑物表面装饰构件对结构风荷载特性的影响研究方面，Montazeri等[7]采用计算流体动力学（computational fluid dynamics，CFD）方法研究了外挑阳台对高层建筑风压分布的影响，结果表明阳台的细部构造对建筑立面的风荷载分布影响很大；Yuan等[8]通过风洞试验模型的研究，发现高层建筑表面附属构件会减小迎风面局部最大正压峰值和侧面局部负压峰值；艾辉林等[9]采用CFD数值模拟技术研究了超高层建筑外表面装饰条的风荷分布规律及其风载控制系数；全涌等[10]进行了建筑局部外形对围护结构风荷载特性影响的试验研究，结果表明最大正风压系数并不受局部外形的影响，但对最大负风压系数的影响较大；沈国辉等[11]研究了设有外镂空装饰的扭转体型高层建筑的风荷载，结果表明装饰结构能明显减小主体结构侧风面风压的平均值和脉动效应.

综上所述，已有关于装饰构件对结构风荷载特性影响的研究主要集中于高层建筑和悬挑结构，针对大跨屋盖，特别是大跨贝壳形屋盖的研究还鲜有报道. 由于大跨贝壳形屋盖与高层建筑以及悬挑结构的结构特性具有很大的不同，主体结构和局部构件的风荷载分布规律也不一样. 因此，亟需对外表面有复杂装饰条的大跨贝壳形屋盖的风荷载特性进行研究，了解表面装饰造型对屋面风压分布的影响，为类似结构的抗风设计提供参考.

在已有关于结构风荷载特性的研究方法中，风洞试验虽然已广泛应用于工程结构的抗风性能评估，但要考虑装饰构件对大跨度结构的影响却非常困难，主要原因在于装饰构件的尺寸相对较小，一般的缩尺模型难以呈现其几何特征，而采用较大的缩尺模型除成本较高之外，一般风洞还难以满足阻塞比的要求. 与风洞试验相比，CFD方法具有可以建立建筑原型尺度、周期短、成本低等优点，已广泛应用于大跨翘曲屋盖、复杂体型高铁站房屋盖、可伸缩大跨体育场馆屋盖等大跨结构的风荷载特性研究[12-15].

为此，本文以某大跨高铁站房屋盖为对象，采用CFD方法，基于高性能计算机工作站和Rhino、Fluent15.0 软件平台，建立了该大跨贝壳形屋盖的数值风洞模型，并采用风洞试验数据对其可靠性和适用性进行验证. 除建立有表面装饰条（surface decorative strips，SDS）的数值风洞模型之外，还建立了无表面装饰条（no surface decorative strips，NSDS）的数值风洞模型，研究了表面装饰肋条对屋盖风荷载特性的影响，并分析了其受力机理.

1 计算流体力学理论

湍流模拟采用工程中常用的雷诺平均法（RANS），并将大气边界层内建筑物周围低速流动的空气视为不可压缩流体，其基本控制动量方程（Navier-Stokes方程）和连续方程[16]分别如式（1）、（2）.

式中：δij为克罗内克（Kronecker）函数；Cμ为经验系数；k和ε如式（5）、（6）.

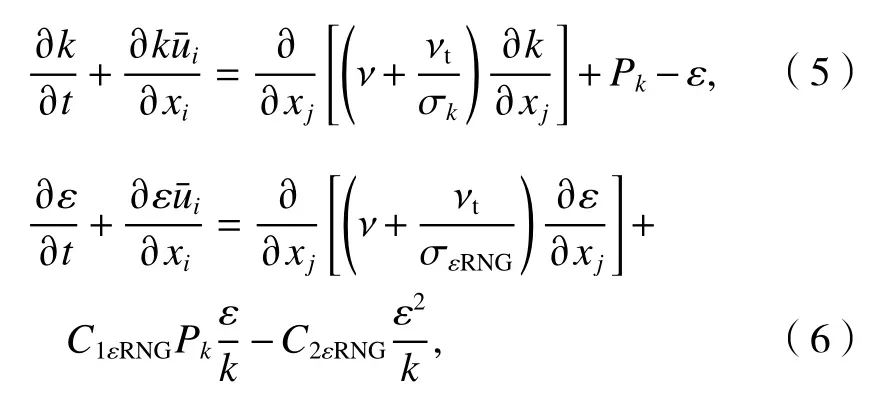
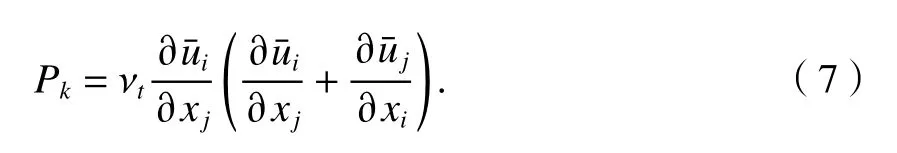
2 数值模型的建立

该屋盖长跨143 m，短跨80 m，矢高24 m，其主体结构采用顺时针和逆时针各36根双螺旋钢箱梁呈空间相交接而成四边形网格，网格内填充有四周向中心有一定拱度的ETFE （ethylene tetra fluoro ethylene）气枕，在屋盖表面设有沿顺时针钢箱梁高出屋面约 50 cm的装饰条，该屋盖整体造型新颖独特，类似于贝壳形，如图1所示[17].

2.1 几何建模及网格划分

由于贝壳形屋盖几何形状较为复杂，几何模型的建立采用Rhino软件进行. 屋盖的几何模型有两种，分别为有表面装饰条模型和无表面装饰条模型. 有表面装饰条模型与实际结构完全一致，装饰条沿钢箱梁螺旋布置，为200 mm × 500 mm的矩形截面，相邻装饰条间最大垂直间距（屋盖底部）为3.965 m，最小间距（屋盖顶部）为0.950 m，除建立了屋盖结构表面的形状之外，还呈现了ETFE气枕（如图2（a）所示）. 无表面装饰条屋盖模型仅考虑屋盖结构表面的形状，主要用作对比分析（如图2（b）所示）.

图1 有表面装饰条大跨贝壳形屋盖（单位：m）Fig. 1 Large-span scalloped roof surface with decorative strips (unit：m)

图2 贝壳形屋盖几何模型Fig. 2 Geometric model of shell-shaped roof

数值风洞模型流体计算域的确定也较为重要，Franke等[18-19]的研究表明：计算域的大小取决于建筑物覆盖区域和边界条件，根据该建筑物的实际尺寸（143 m（长） × 80 m（宽） × 24 m（高）），结合计算条件，将计算域取为1 200 m（长） × 800 m（宽） × 300 m（高）. 建筑物中心（结构平面长短轴交点）位于流场沿流动方向1/3处，中心距入口边界5B，距出口边界10B，距侧面边界5B，距顶面边界10H，B和H分别为建筑物的宽度和高度，如图3所示. 该数值风洞的阻塞率为0.57%，小于风洞试验建议的3.00%，可以满足模拟建筑物所处大气环境的要求[20].

图3 数值风洞的流体计算域和边界条件（单位：m）Fig. 3 Fluid calculation domain and boundary conditions of numerical wind tunnel (unit: m)

在进行网格划分时，采用了外流域使用结构化网格，建筑物表面使用非结构化网格的混合离散方法，网格尺寸随距建筑物边界距离的增大而增大. 相对于无表面装饰条屋盖，有表面装饰条屋盖由于表面装饰条的存在，更加注重网格的精细化要求，对装饰条及ETFE气枕进行局部精细化加密. 运用处理软件ICEM CFD 进行网格划分，有表面装饰条屋盖共划分网格单元3428941个，装饰条旁最小体网格体积为1.178 × 105mm3，远处最大体网格尺寸为6.034 × 107mm3. 无装饰条屋盖共划分网格单元 2657728个，屋面局部网格划分情况如图4所示.

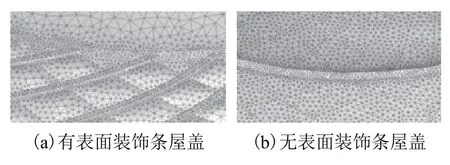
图4 屋盖表面局部网格划分情况Fig. 4 Local meshing of the roof surface

2.2 边界条件与求解

数值风洞的边界条件如图3所示. 入口边界条件采用速度入口（velocity-inlet）模拟D类大气边界层风剖面，平均风速剖面、k和ε在入流口的分布均采用UDF编程与Fluent作接口实现. 出口边界条件采用完全发展出流边界条件（outflow），即流场任意物理量沿出口法向梯度为0. 计算域顶部和两侧采用对称边界条件（symmetry）来等价黏性流动中的无滑移壁面. 建筑物表面和地面采用无滑移的壁面条件Wall. 为计算方便，入口处湍流参数采用k和ε组合在边界上赋值，如式（8）、（9）[20].

式中：V（Z）为平均风速，V（Z） =V10（Z/10）α，V10为模型前方来流未扰动区离地面10 m高度处的平均风速，α为地面粗糙度指数，取值 0.3；Z为离地高度；I为湍流强度；l为湍流积分尺度.

结合风洞实测数据，高度Z处的I和l计算如式（10）、（11）.

为保证计算的稳定性，对流项的离散选用了具有三阶精度的二次迎风插值格式，速度压力耦合采用SIMPLEC算法，同时各变量收敛残差控制到10−5以下，以保证求解的精度.

3 数值模型的试验验证及分析

3.1 风洞试验概况

试验在西南交通大学风工程试验研究中心XNJD-3大气边界层风洞中完成，风洞试验段尺寸为36.0 m（长） × 22.5 m（宽） × 4.5 m（高）. 为考虑屋面装饰条，模型缩尺比例取为1∶75，采用尖塔和立方体粗糙元组合的方法模拟D类风场，模型如图5（a）. 风场风速比与湍流度剖面如图5（b）所示（图中：ZG、U、UG分别为参考点高度、风速和参考点处风速；Iu为湍流强度）.

图5 模型在风洞中的情况Fig. 5 Model in the wind tunnel

屋盖结构表面共计布置673个测点，试验风速为7 m/s，每个测点采样时间为150 s，采样频率为200 Hz. 试验风向角间隔为15°，共计测量了24个风向角，如图6所示. 图中：a1～a18、b1～b12均为测点. 每风向重复测量2次，所有压力测点的脉动压力时程同步获得. 试验结果表明，风荷载作用下，屋盖以升力为主，屋盖顶部区域风压系数较大，各风向角下屋盖顶部周边区域的局部体型系数较其他区域大，屋盖陡端区域局部体型系数较缓端局部体型系数大[16].

图8 风压系数偏差比随测点的变化曲线Fig. 8 Variation curve of deviation ratio of wind pressure coefficient with measuring points

从图7、8中可以看出：试验值与计算值变化趋势基本一致，总体而言，短轴方向平均风压系数试验值与计算值的差异较长轴方向小，270° 风向角较 0°风向角的差异小. 长轴方向：0° 风向角时，处于尾流区的远端测点a1～a4的平均风压系数试验值与计算值的差异较大，风压系数偏差比大于0.5，尾流区尾端测点a1的风压系数偏差比约为1.2，其余测点风压系数偏差比在 ± 0.5以内，说明数值模型对于尾流区的模拟仍有待于进一步研究；270° 风向角时，偏差比在 ± 0.26以内，长轴方向屋面缓端测点a10～a18的计算值比试验值要高一些，主要原因可能在于测点附近装饰肋条的旋转方向为阻风向，气流在局部的流向及流速会产生突变，在屋盖上形成具有较高吸力特性的涡流，使得风压系数计算值的绝对值大于风洞试验. 短轴方向：0° 风向角时，偏差比在 ±0.18以内；270° 风向角时，偏差比在 ± 0.31以内.

3.2.2 屋面风荷载体型系数

为了解风荷载体型系数计算值与试验值之间偏差情况，定义风荷载体型系数相对误差为

式中：us,Exp为风荷载体型系数试验值；us,Sim为风荷载体型系数计算值.

将整个屋盖分为27个区域， 0° 及270° 风向角下，经数值模拟和风洞试验所得到的屋盖局部区块风荷载体型系数分布情况如图9所示，图中无框数字为数值计算结果，方框内数字为风洞试验结果. 从图中可以看出：0° 风向角时，来流侧屋盖前段的4个区块的风荷载体型系数为正值，其余区块的风荷载体型系数均为负值；270° 风向角时，除来流侧的近端区块风荷载体型系数为正值外，其余区块的风荷载体型系数均为负值. 屋盖各区块风荷载体型系数计算值与试验值的分布规律基本一致，风荷载体型系数大都为负值，以吸力为主，说明贝壳形屋盖与圆球屋盖及椭球屋盖等大跨度结构具有相似风压分布风特性[21-22]；0° 风向角时，除尾流区外，风荷载体型系数计算值略大于试验值，屋盖顶部区块的风荷载体型系数最大，风荷载体型系数试验值为 −0.51，计算值为−0.54；270° 风向角时，在屋盖的缓端及迎风面，风荷载体型系数计算值略大于试验值，风荷载体型系数最大值出现在屋盖顶部周边区块，风荷载体型系数试验值为−0.69，计算值为−0.71.

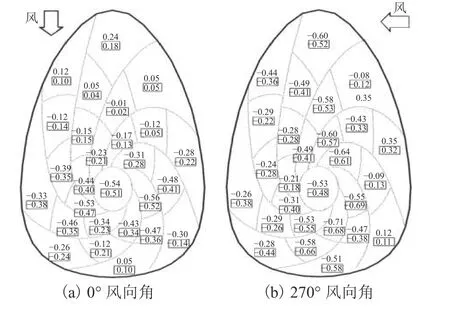
图9 屋盖局部区块风荷载体型系数分布Fig. 9 Distribution of wind load shape coefficient of local block in the roof

在0° 及270° 风向角下，屋盖各区块风荷载体型系数相对误差如图10所示. 0° 风向角下，除屋面正负压过渡区域风压本身较小不具有参考价值，尾流区的数值模拟存在局限性[23]，相对误差较大之外，其余区块的风荷载体型系数相对误差在 ± 25%以内. 与0° 风向角类似，270° 风向角下，除屋面正负压过渡区域及尾流区的相对误差较大之外，其余区块的风荷载体型系数相对误差也在 ± 25%以内.

图8 风压系数偏差比随测点的变化曲线Fig. 8 Variation curve of deviation ratio of wind pressure coefficient with measuring points

3.2.2 屋面风荷载体型系数

为了解风荷载体型系数计算值与试验值之间偏差情况，定义风荷载体型系数相对误差为

式中：us,Exp为风荷载体型系数试验值；us,Sim为风荷载体型系数计算值.

图9 屋盖局部区块风荷载体型系数分布Fig. 9 Distribution of wind load shape coefficient of local block in the roof

图10 风荷载体型系数相对误差Fig. 10 Relative error of wind load shape coefficient

综上所述，数值模拟结果与风洞试验结果除在屋盖正负压过渡区和尾流区存在较大差异之外，0°风向角时，长轴方向的测点风压系数的偏差比在± 0.50以内，短轴方向的偏差比在 ± 0.18以内，270°风向角时，长轴方向的测点风压系数的偏差比在± 0.26以内，短轴方向的偏差比在 ± 0.31以内；0°及270° 风向角下，风荷载体型系数相对误差均在± 25%以内.

4 装饰条对屋面风荷载特性的影响

为研究装饰条对贝壳形屋盖表面风荷载特性的影响，分别建立了某高铁站房贝壳形屋盖的有表面装饰条和无表面装饰条的数值风洞模型，并分别进行了数值模拟计算. 通过对各风向角下的风荷载升力系数、风荷载局部体型系数和速度矢量图的对比分析，探讨装饰条对贝壳形屋盖风荷载特性的影响.

4.1 风荷载升力系数

对有装饰条模型采用数值模拟和风洞试验得到了各风向角下的风荷载升力系数，对无装饰条模型采用数值模拟计算升力系数. 此处，将风荷载升力系数定义为屋盖所受竖向风荷载与屋面标准风荷载之比，如式（16）.

式中：βj为第j种情况时的风荷载升力系数，此处j取1、2、3，分别为有装饰条模型数值计算、有装饰条模型风洞试验和无装饰条模型数值计算，余同；Fj为第j种情况时屋盖所受竖向风荷载；V为来流风速；A为屋面参考面积.

各风向角下，风荷载升力系数及偏差率见表1.从表中可以看出：有表面装饰条模型数值计算与风洞试验结果相比，二者的差异较小，风荷载升力系数偏差率在−7.1%～6.1%之间；有表面装饰条模型风洞试验结果与无表面装饰条模型数值计算结果相比，各风向角下，无表面装饰条模型的风荷载升力系数要大一些，偏差率在1.5%～22.4%之间，当风向角为90° 和270° 时，由于装饰条的旋转方向为阻风向且阻挡面积最大，偏差幅度较大，当风向角为0°和180° 时，二者的差异较小；有表面装饰条模型数值计算结果与无表面装饰条模型数值计算结果相比，除180° 风向角下，二者基本相同之外，其余各风向角下，均为无表面装饰条模型的风荷载升力系数偏大，偏差率在−0.8%～22.4%之间，当风向角为90° 和270° 时，偏差率较大，当风向角为0° 和180°时，二者的差异较小.

表1 各风向角下的风荷载升力系数及偏差率Tab. 1 Wind load lift coefficient and deviation rate undereach wind direction angle

风荷载升力系数随风向角的变化情况如图11所示，从图中也可以明显看出：各风向角下，有表面装饰条模型数值计算结果与风洞试验结果之间的差异较小，而与无表面装饰条模型数值计算结果之间的差异随风向角有较为明显的变化，当风向角为90° 和270° 时，偏差率较大，当风向角为0° 和180°时，二者的差异较小.

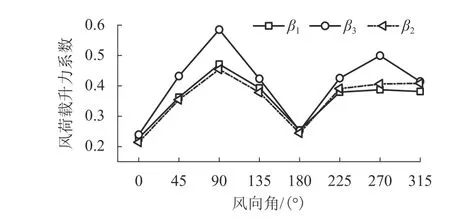
图11 风荷载升力系数随风向角的变化情况Fig. 11 Variation of lift coefficient of wind load with wind direction angle

总体说来，有表面装饰条的贝壳形屋盖较无表面装饰条的风荷载升力系数小，说明表面装饰条对于大跨度贝壳形屋盖的整体抗风是有利的，这与Letchford等[24]的结论基本一致.

4.2 风荷载局部体型系数

为了解装饰肋条对屋盖局部围护结构风荷载特性的影响，将整个屋面以相邻4块ETFE气枕划分为一个区块，整个屋盖总计有的235个区块，区块编号分别为1、2、···、235，区块总体划分情况如图12所示. 风荷载局部体型系数的计算方法与风荷载体型系数的计算方法类似，此处不再赘述.

图12 风向角及细部区块定义Fig. 12 Definition of wind direction angle and detailed block

采用数值模拟方法分别计算有表面装饰条模型和无表面装饰条模型的风荷载局部体型系数（Us1），图13为典型风向角（0° 和270°）下各区块的风荷载局部体型系数随区块的变化曲线. 从图中可以看出：装饰条对风荷载局部体型系数的影响程度与风向角有关，0° 风向角时，装饰肋条对局部风压的影响较大，270° 风向角时，装饰肋条对局部风压的影响较小. 在迎风面，装饰肋条对风荷载局部体型系数的影响较小，二者较为接近，越靠近屋盖顶部二者差异越大. 在两侧绕流区域和尾流区域，有表面装饰肋条屋盖的风荷载局部体型系数小于无表面装饰肋条屋盖. 同时，无论是正压还是负压，有表面装饰肋条屋盖的风荷载局部体型系数都要小于无表面装饰肋条屋盖.

为了解装饰肋条对屋面局部风压的影响程度，定义风荷载局部体型系数偏差比为

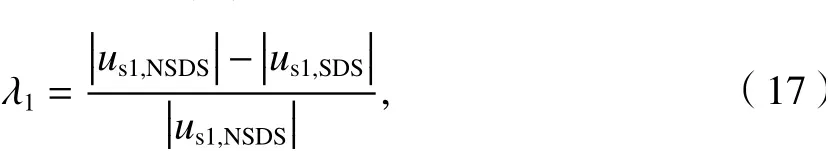
式中：usl,NSDS为无表面装饰肋条屋盖风荷载局部体型系数；usl,SDS为有表面装饰肋条屋盖风荷载局部体型系数.

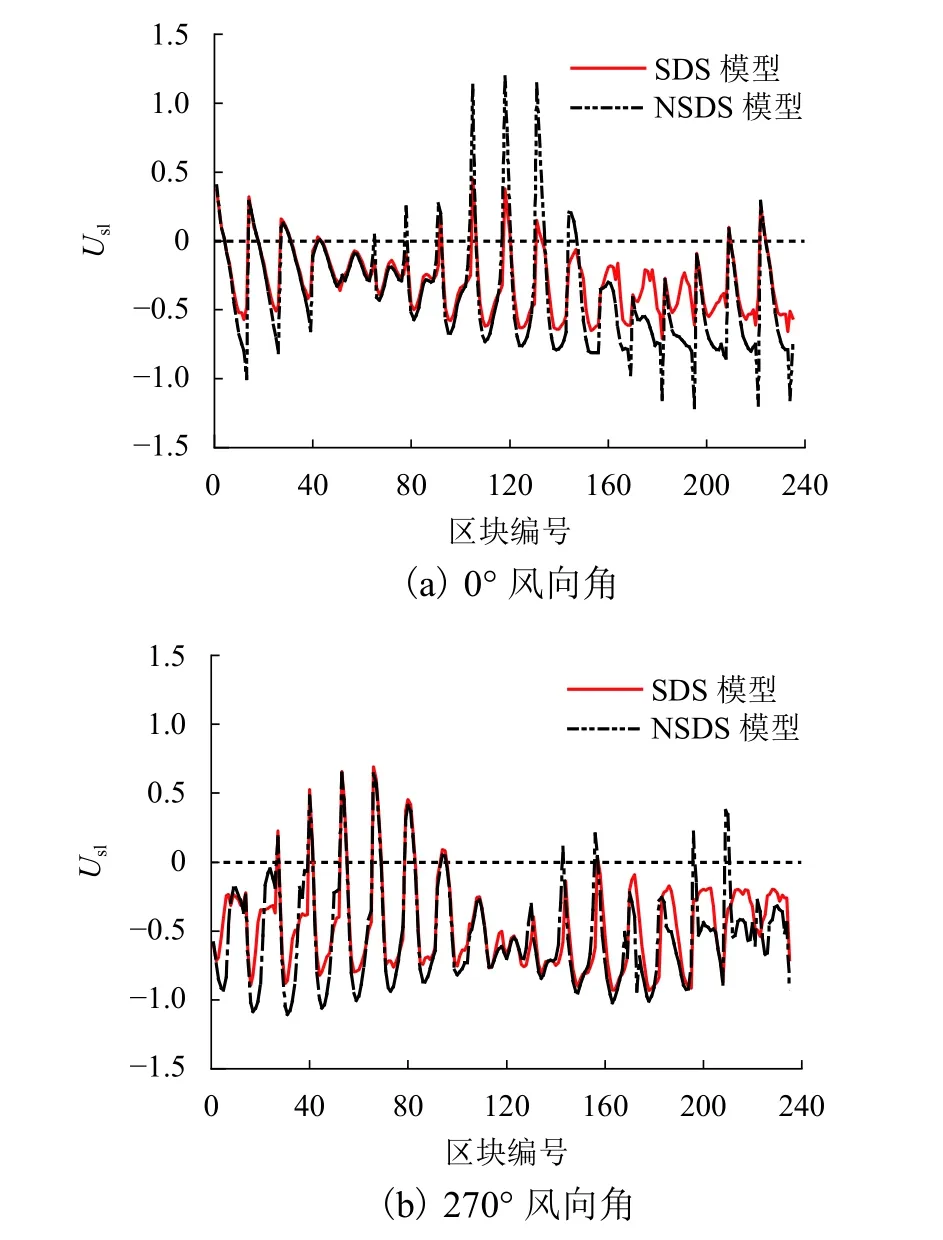
图13 风荷载局部体型系数随区块的变化曲线Fig. 13 Variation curve of local shape coefficient of wind load with block size

图14为风荷载局部体型系数偏差比随区块的变化曲线. 从图中可以看出：各风向角下，装饰条可以减少大部分区块的局部风压，同时也会使个别区块的局部风压增大. 与无表面装饰肋条屋盖相比，0°风向角下，设置装饰肋条可以减小屋面局部风压50%左右，同时会使得个别区块的风压最大增加4.5倍左右，270° 风向角时，大部分区块的风荷载局部体型系数偏差比在0～0.5之间，个别区块的风荷载局部体型系数偏差比较大，最大值接近−5.0.

综上所述，装饰肋条并未改变大跨度贝壳形屋盖以吸力为主的风荷载作用机制，与无表面装饰肋条相比，设置装饰肋条可以使屋面大部分区域的局部风压减小0～50%左右，但也会使得屋面个别区域的风压增大最大达5倍，在对局部附属构件的设计时应予以重点关注.

4.3 装饰肋条对屋盖风荷载特性的影响机理

为深入了解屋面装饰肋条对贝壳形屋盖影响机理，本文以屋盖顶部附近典型区域part 1 （见图12）为例，分析装饰肋条对风压系数分布和风速矢量的影响.

图14 风荷载局部体型系数偏差比随区块的变化曲线Fig. 14 Variation curve of deviation ratio of local shape factor of wind load with block size

4.3.1 局部区域风压系数分布

图15为0° 风向角下的屋面part 1的风压系数分布情况. 从图中可以看出：在屋面顶部边缘处，无表面装饰条屋盖的风压系数在−0.70～−0.90，有表面装饰条时为−0.60，减小风压15%～33%；带有肋条区域总体来讲是肋条处的风压系数较大，为−0.80，肋条之间风压系数较小，为−0.40～−0.60，无表面装饰肋条的风压系数为−0.55～−0.70. 图16为270° 风向角下的屋面part 1的风压系数分布情况.从图中可以看出：无表面装饰条的屋顶风压系数为−0.24～−0.38，有表面装饰条屋顶为−0.15～−0.30，风压降幅在27%～37%；无表面装饰条的屋面风压系数为−0.22～−0.34，而有表面装饰条屋面为−0.10～−0.20，风压降幅在40%～55%，而带有装饰条区域依然是肋条处的风压系数较大，为−0.40. 出现这种较大差异的原因可能在于装饰肋条之间存在一定的狭管效应以及肋条对风流的阻挡作用，装饰肋条的设置会导致肋条自身的局部风压较大，在设计时务必予以重点注意，同时，又可以降低无肋条区域的表面风压15%～50%左右，这对ETFE气枕的抗风是有利的.

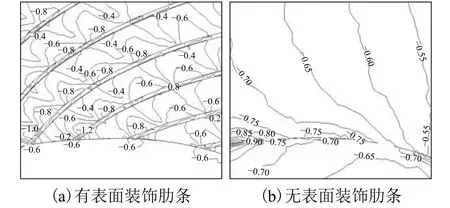
图15 0° 风向角part 1风压系数分布Fig. 15 Wind pressure coefficient distribution of part 1 under 0° wind angle

图16 270° 风向角part 1风压系数分布Fig. 16 Wind pressure coefficient distribution of part 1 under 270° wind angle

4.3.2局部区域速度矢量分布

图17为屋面在0° 风向角下part 1区域的屋盖表面风速示意. 从图中可以看出：相较于无表面装饰条屋盖，装饰肋条之间具有一定的狭管效应，肋条对风流的阻挡效应致使风流在肋条处有明显的漩涡产生，这种漩涡可能对风速有放大作用，从而使得肋条处的风压较高，风压存在突变现象. 由于装饰肋条呈螺旋形，风向角对装饰肋条间的狭管效应以及肋条阻挡效应影响也较大. 0° 风向角下，肋条和屋盖表面的风流均随螺旋形肋条的旋转改变，图中非常清楚的显示了装饰肋条之间的狭管效应及导流作用.

图17 0° 风向角下part 1速度示意Fig. 17 Velocity vector of part 1 for 0° wind direction angle

图18为0° 风向角下10 m高度处水平风速矢量图. 可以看出：有表面装饰条屋盖由于装饰条的存在导致侧面来流的分离而在背风面形成小区域尾涡，无装饰条屋盖则来流附着屋盖表面流动，背风面无尾涡形成；图19为270° 风向角下10 m高度处水平风速矢量图，两种模型均在背风面形成对称尾涡，但有装饰条屋盖尾涡区域要大于无装饰条屋盖，这是由于此风向角下建筑物侧面绕流明显，而装饰条的存在加剧了来流分离，从而在背风面形成较大尾涡区.