不同粗糙度岩体节理面的应力松弛特性及机理

王 振 ，顾琳琳 ，沈明荣

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007；3. 南京理工大学理学院，江苏 南京 210094；4. 同济大学土木工程学院，上海 200092）

应力松弛为变形不变、应力随时间减小的性质，是岩体时效特性的重要方面. 在实际工程中，如地下洞室开挖过程中，围岩中应力和变形均随开挖的进行而不断变化[1]，大部分情况下，洞室围岩处于变形比较明显的蠕变状态，当衬砌刚度较大，围岩变形受到限制时，围岩中的应力会随着时间的推移而逐渐释放，出现应力松弛现象，这种应力的调整，会导致岩石内部的损伤，并形成连续的破坏带[2]. 因此，岩体的应力松弛特性对工程的长期稳定和安全同样具有重要的影响.

节理面是岩体的重要组成部分，其力学特性往往控制着岩体工程的稳定. 目前对岩体节理面应力松弛特性已有一定的研究，如Fahimifar等[3]对人工砂岩齿形结构面进行了应力松弛试验，试验成果表明，包含锯齿的节理面应力松弛特性要比平整或分离结构面的应力松弛特性明显的多；刘昂等[4-5]分别对表面形态为不同粗糙度的Barton标准剖面线和锯齿形的人工模拟节理面试样开展了等应力循环加载剪切应力松弛试验和分级加载应力松弛试验，初步揭示了节理面的应力松弛特征. 对于应力松弛机理的研究，目前的文献中主要针对完整岩石，对于节理面应力松弛机理的研究还相对较少；Peng[6]通过对Arkose砂岩、Tennessee大理石和Berea砂岩开展应力松弛试验，得到了应力松弛过程中会使试样内部断裂的增长趋于稳定，承载能力下降是为了防止其发生轴向位移的结论；陈宗基等[7-8]认为应力松弛与裂纹的增长、接合和产生而导致的结构变化有关，并且应力松弛是间断的和阵发式的，其原因是岩石内部破裂面相互滑动、裂纹扩展和新裂隙产生的综合作用；于怀昌等[9-10]的研究中也推测完整岩石的应力松弛现象与其破裂机制和损伤有关；Paraskevopoulou等[11]在试验和前人研究成果的基础上证实了裂隙发展是造成应力松弛的主要原因. 上述文献主要针对完整岩石的应力松弛机理进行了研究，并且得出应力松弛的主要原因是裂隙的产生和发展，而岩体节理面的应力松弛特性受到其表面粗糙度（JRC）及剪切应力等因素的影响，剪切过程中存在着爬坡和剪齿等作用，其机理更为复杂. 因此，需要详细的研究岩体节理面的应力松弛特性，进一步揭示岩体应力松弛机理.

1 试验方案

1.1 试验设备

节理面剪切应力松弛试验采用长春试验机研究所研制的CSS-1950岩石双轴流变试验机（见图1），该试验机采用双向压力伺服控制，垂直轴最大压缩荷载为500 kN，水平轴最大压缩荷载300 kN，可采用位移传感器（LVDT）同时测量试样双侧的变形值，可实现加载速率控制和应变速率控制2种方式.试验机通过伺服控制系统，实现了保持试样变形恒定的条件下其应力的自由松弛.

图1 岩石双轴流变试验机Fig. 1 Biaxial rheological test machine

1.2 试验样品

本文目的在于研究粗糙度对岩体节理面的应力松弛特性及其产生的机理，而自然界中天然岩体节理面的表面形态变化较大，其多样性和差异性不利于规律的总结和归纳，因此，选择水泥砂浆作为试验材料，按照标准Barton剖面线，将不同粗糙度节理面加工成钢模（见图2[2]），浇筑试件：水泥砂浆选用325水泥，标准砂和水，配合比为2∶4∶1，试样成型时间24 h，养护28 d，养护温度（20 ± 1） ℃，养护湿度大于95%. 试块尺寸为10 cm × 10 cm × 10 cm. 本文采用Barton 1、4、10号剖面，如图3（a）所示，3种剖面从平整到粗糙，粗糙度差别较大. 浇筑完成的试样如图3（b）所示. 对立方体试块进行单轴抗压试验，单轴抗压强度为21.73 MPa.

图2 试样制作过程Fig. 2 Sample preparation process

图3 试验中的采用巴顿曲线剖面及试验样品Fig. 3 Barton’s standard profile lines and sample for test

立方体试样作为对比试样，也按照上述实验过程对其进行了剪切应力松弛试验.

对节理面试样开展了法向应力为6.52 MPa的直剪试验，其剪切强度如表1所示. 由表可知，粗糙度增加，其剪齿现象增强，由节理面剪齿所提供的强度组份增加[12]，该剪切强度可作为选择分级加载应力松弛试验分级应力的依据.

表 1 不同粗糙度节理面的剪切强度Tab. 1 Shear strength of joints with different JRCs

1.3 试验过程

分级加载剪切应力松弛试验在恒温恒湿的条件下进行（温度（20 ± 1） ℃，湿度50 ± 2%），法向应力选择单轴抗压强度（UCS）的30%，即6.52 MPa，水平剪切应力的分级标准参考瞬时剪切强度，按照瞬时剪切强度的50%、60%、70%、80%、90%、100%（由于试样之间的差异性，部分节理面强度较大可能达到该强度值）选取分级加载应力松弛试验的分级应力，直到某一应力水平下试样在加载过程中破坏.试验过程中，首先施加法向应力，待法向变形稳定时保持其应力恒定，之后按照0.5 MPa/min的加载速度加载至预定的应力水平，如图4所示. 图中：D为剪切变形；t为时间；实线为加载阶段（加载速率0.5 MPa/min），虚线均为松弛阶段（应力增量Δτr为剪切强度的10%，每级持续时间Δt= 72 h）. 通过试验机的伺服系统，保持试样对应的变形不变及应力的自由松弛，然后施加下一级应力. 每级应力松弛持续72 h. 试验过程中，通过伺服系统对试样法向及水平方向的应力和变形进行记录，分级加载剪切应力松弛试验如表2所示. 表中：i= 1，2，···，6，破坏应力为试验过程中试样发生破坏的应力.

图4 分级松弛试验加载过程示意Fig. 4 Schematic diagram of loading process in the multi-stage stress relaxation test

表2 分级加载剪切应力松弛试验应力表Tab. 2 Shear stresses of multi-stage relaxation tests

2 试验成果

2.1 分级加载剪切应力松弛试验全过程曲线

按照上述试验方案，分级加载应力松弛试验共进行4块试样，其中1号节理面（JRC = 1）、10号节理面（JRC = 19）分别进行了6级试验，在第7级试验时，试样在加载过程中破坏，而4号节理面（JRC =7）和完整试样在第6级加载段发生破坏. 分级加载剪切应力松弛试验的全过程曲线如图5所示. 图中：σn为法向应力.从图5可以看出：

1） 不同粗糙度节理面的剪切应力松弛曲线形态基本相似，即应力随时间降低，曲线趋于平缓，这表明应力松弛速率也随时间逐渐降低；

2） 在分级加载情况下，每级应力对应的松弛应力随着初始应力的升高而升高，但不是线性增加的，如图5中A、B虚线所示，初始应力（曲线A）线性增加，剩余应力（剩余应力为应力松弛以后尚存在于节理面内部的应力，即传感器的视值）的连线（曲线B）为非线性，即初始应力越大，松弛掉的应力越多，其剩余应力的连线呈现下凹型（如曲线B所示）；

图6为松弛应力与初始应力的关系. 由图6可知：松弛应力随着初始应力的升高先略有减小后增大，应力超过某个“阈值”以后，松弛应力急剧增加. 该现象的出现与节理面的应力及变形状态有关.节理面在较低应力水平下为压密状态，弹性变形为变形的主要部分，整个节理面的剪切刚度增加，节理面的力学性质呈现“硬化”的趋势[13]，此时试样本身的储能能力及抗破坏能力增强，其“释放应力”的能力减弱，因而出现了松弛应力减小的情况，但当应力超过一定值时，节理面中裂隙出现不稳定发展，新的裂隙也开始产生，即塑性变形成为了主要的变形方式，节理面工程性质开始劣化，其储能能力减弱. 因此，高初始应力条件下一方面造成了裂隙的发展进而增加了应力松弛的通道，试样对应力的“束缚”能力降低，并同时降低了节理面的储能能力；另一方面又提供了较大的能量输入，节理面需要释放更多的能量以保持试样的相对稳定.

图5 分级加载剪切应力松弛试验全过程曲线Fig. 5 Complete curves of multi-stage loading relaxation tests

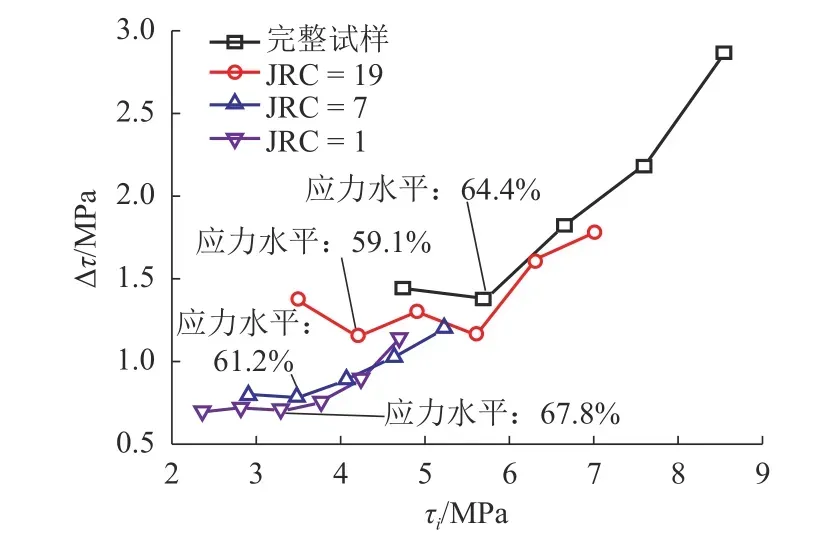
图6 总松弛应力与初始应力之间的关系Fig. 6 Relationships between total relaxation stress and initial stress

为了更清楚的反映松弛应力与JRC的关系，图7中给出了松弛应力与初始应力的比值与应力比（初始应力/峰值应力）的关系，换算为比例关系以后，上述现象更加明显，如图7所示，随着初始应力的增加，Δτ与τi的百分比随着初始剪切应力的增加先减小后增大，并且随着粗糙度的增加，该现象越来越明显，其转折点的应力比与粗糙度相关，粗糙度越大，同样的应力比条件下，松弛应力与初始应力的比值具有升高的趋势.

图7 松弛应力/初始应力与初始应力/峰值应力的关系Fig. 7 Relationships between the relaxation stress to initial stress ratio and the initial stress to peak stress ratio

声发射监测表明，岩体在应力松弛过程中伴随着裂隙的发生和扩展[14]，节理面在剪切过程中存在着“爬坡”和“剪齿”等效应，JRC越大“剪齿”效应越明显，裂隙发生和发展的“空间”也就越大.当裂隙扩展不是优势变形方式时，初始阶段的硬化现象导致试样“应力松弛能力”降低，而当应力大于某个“阈值”应力以后，由于裂隙的不稳定发展，试样工程性质劣化，节理面的“应力松弛能力”增加. 当JRC较大时，剪切过程中可硬化或者裂纹发展的“空间”增加，这也是JRC越大，节理面“松弛能力”随应力的升高而变化更加明显的原因. 完整试样具有更高的松弛能力及变化幅度也同样证明了上述论断.

2.2 分级加载剪切应力松弛曲线及应力松弛速率特征

图8为分级加载剪切应力（τ）松弛试验曲线，从应力松弛曲线的形态来看，大部分应力松弛曲线光滑，表现出了连续型的松弛特征，但是部分应力松弛曲线（如图8中标注的E处）发生了应力突然跌落的阶梯型变化.

图8 分级加载剪切应力松弛曲线Fig. 8 Shear stress relaxation curves with multi-stage loading

对应力松弛曲线上的各点求导，可得到应力松弛速率（v）曲线，如图9所示. 从图中可以看出：应力松弛速率在初始阶段比较大，但其衰减速度非常快，短时间内速率衰减到一个较小的值，之后开始比较缓慢的衰减，并且衰减的速率越来越慢；应力松弛速率衰减到一定值以后，其衰减速率比较缓慢，在一定的时间内看不出明显的变化，可以认为该阶段的松弛速率相等，反映在应力松弛曲线上为近似的线性段，但是整个阶段应力松弛速率仍然具有减小的趋势，最终减小为0，反映在应力松弛曲线上表现为近似水平.

图9 分级加载剪切应力松弛速率曲线Fig. 9 Shear stress relaxation rate curves with multi-stage loading

结合图8中标注的转折点前后的曲线形态可以看出：在初始应力作用后，应力快速降低，表现出了应力跌落的形态，该阶段应力松弛曲线表现出了非常明显的非线性特征，因此该阶段可称为非线性衰减应力松弛阶段（R1）. 当应力松弛到一定程度后，较小的应力松弛速率导致应力释放缓慢，并且曲线在有限时间内表现出了近似的线性特征，该阶段为松弛第2阶段（R2）. 需要说明的是，应力松弛第2阶段的曲线形态并不是绝对的线性关系，曲线仍然会表现出局部的跌落和震荡，并且近似直线段的斜率也会随着时间的推移缓慢的减小，但整体上应力释放速率稳定，该阶段可定义为稳态应力松弛阶段. 当应力松弛速率降低到一定程度以后，其量值趋向于0，应力松弛曲线表现出了近似水平的形态，此时节理面内部的应力基本不再调整，松弛停止，此阶段称为应力松弛结束阶段（R3）.

如图10为初始速率与应力比的关系. 由图可知：初始速率随应力的增加而增加，当应力水平超过某个级别时，速率会迅速的上升，JRC越大，该现象越明显，同样的应力百分比条件下，JRC越大，应力松弛的初始速率也就越大，这是由于节理面JRC增大，剪切过程中“切齿”效应的增加会导致其储能能力增强，同时由于较大的初始应力也使其储存了大量的弹性能，形成了较高的弹性势能，在开始松弛的瞬间，初始速率也就越大；初始速率（初始势能）与初始应力为非线性关系，并且粗糙度越大，这种非线性关系越明显.

图10 初始松弛速率与应力比的关系Fig. 10 Relationships between initial stress relaxation rates and stress ratio

3 剪切应力松弛试验现象及其机理解释

剪切应力松弛试验所采用的CSS-1950双轴流变试验机及水平荷载控制系统（伺服电机和谐波减速器）如图11所示. 在剪切应力松弛试验过程中，首先试验机对试样施加垂直荷载，待变形稳定后施加剪切荷载至预定值，试验机依靠不断调整水平压头的位置保持变形不变，应力随时间开始下降. 在试样应力达到目标值并且保持变形恒定后，减速器会进行向后-向前来回转动的过程（如图中C、D，C表示转动速率相对较快，D表示转动速率相对较慢），并且这种现象开始比较频繁，即减速器及伺服电机转动次数较多，转动时间相对较长，此时应力降低比较剧烈；在应力松弛一段时间后，该现象变得不明显，调速器转动速度逐渐变慢，转动的频率也随之降低，有时只是轻微的来回晃动，转动时间也变得比较短.

图11 应力松弛过程中的试验机响应Fig. 11 Response of test machine during stress relaxation

上述响应过程是试验机为保持试样变形不变而自身调整引起的. 试样在恒定的剪切力作用下必然会产生蠕变的趋势，这时如果试验机不加以控制，那么试样会迅速地变形. 如果保持其变形不变，那么试验机需要克服蠕变变形，将加载杆的位置保持在初始变形状态，此时加载设备需要通过水平荷载控制系统对试样的剪切变形进行调整. 然而，在控制精度以外，减速器会向前略有转动（现象D，蠕变趋势），当蠕变变形大于系统的控制精度时，变速器开始启动才会启动克服蠕变变形的行为，这时会产生现象C.

从上述仪器在试验过程中反应的描述可知：在应力松弛过程的某一时刻，如果试样所受的应力为τ，在t～t+ Δt时间内产生的蠕变变形量为D，则在该微小时间段内，试件应力可视为恒定值，发生的变形可视为应力为τ的蠕变过程，当控制精度较高，Δt非常短，仪器能够较好地控制试样的蠕变趋势，及时地调整变形，保证变形恒定，然而，即使是微小时间内的蠕变，试样内部已经产生了塑性变形，此过程的能量消耗使应力降低，并且维持该试样同样的变形已经不需要那么高的应力，试样内部抗力的减小造成了应力松弛现象，在应力减小后会继续重复上述过程直至节理面没有蠕变的趋势而变形稳定.同时，随着松弛的进行，应力降低，蠕变趋势减弱，图中C、D现象出现的频率也随之降低. 因此，应力松弛过程可等效为多个微小时间段克服蠕变的行为. 因此，从机理上说，蠕变和应力松弛具有“同源”性. JRC越大，同等应力水平下其可蠕变空间越大，蠕变性能也就越大[12]. 同样的在应力松弛条件下，由于试样的蠕变趋势增强，其表现出的应力松弛现象也越明显.

通过试验机的响应过程，可清晰地反映岩体节理面的应力松弛过程，在实际工程中，当支护结构或岩体刚度较大时，在围岩应力松弛过程中其蠕变趋势受到限制，支护结构通过与围岩之间不断的能量交换，不断地克服围岩的蠕变趋势，但在此过程中，由于蠕变趋势的存在，会引起自身裂隙萌生、扩展，进而出现应力松弛现象. 但由于现场影像因素更加复杂，需要在上述试验和解释的基础上进一步开展现场实验，对现场围岩的应力松弛机制进行研究.

4 结 论

本文通过分级加载剪切应力松弛试验，对具有不同粗糙度的岩体节理面的剪切应力松弛特性进行了详细的分析，结合试验现象对剪切应力松弛机理进行了分析. 通过上述试验结果及分析可以得到以下结论：

1） 剪切应力松弛曲线可以分为3个阶段，即非线性衰减应力松弛阶段、稳态应力松弛阶段及应力松弛结束阶段，其中非线性衰减应力松弛阶段，应力松弛速率不断衰减，应力快速下降，在稳态阶段，松弛速率在一定的时间范围内变化不大，剪切应力松弛曲线近似呈线性；

2） 由于低应力下试样以压密、硬化作用为主导，松弛量随着初始应力的提升呈现出了先略有减小后增加的趋势，并且由于节理面粗糙度为节理面裂隙发展提供了空间，因此其表面形态是影响该变化规律的重要因素；

3） 从试验机的响应过程来看，岩体节理面的应力松弛试验中，试样在长期的剪切应力作用下依然存在着类似蠕变的趋势，其内部仍然有裂隙发展，试验机在此过程中为保持变形不变而不断调整，从而引起应力下降.

4） 岩体节理面的粗糙度越大，同样应力水平下，松弛应力越大，其应力松弛现象表现的越明显.

致谢：岩土及地下工程教育部重点实验室开放研究基金项目（KLE-TJGE-B1903）.