自动驾驶车辆行进参数有限时间估计方法研究

郭其涛

（1.长春汽车工业高等专科学校，吉林 长春 130013；2.第一汽车集团公司教育培训中心，吉林 长春 130013）

1 引言

自动驾驶车辆在保证车辆行驶安全性的前提下，能够大幅减少人为操控失误、提高现有道路的车辆通行效率[1]，并在一定程度上降低运送单位质量货物的能源消耗，减少污染物排放。为了确保行车安全，要求对车速的控制要非常精准，而车速控制不仅与自主车本身的参数相关，还与道路的起伏情况密切相关，因此准确获取这些参数是车辆在复杂环境中自适应路面附着变化并进行安全行驶的关键[2]。现有环境感知方案中，单一传感器很难应对复杂多变的行驶环境，因此无人车系统大多通过将激光雷达与其他多种不同类型的传感器数据融合来进行复杂场景的处理和判断，以实现准确高效地环境感知[6]，但其传感器设备花费不菲，使得成本问题成为了制约自动驾驶技术普及的瓶颈。因此，在一定硬件基础上，结合参数估计实现自动驾驶车辆高效环境感知，是有效、可行的途径之一。

车辆自身的参数估计对自动驾驶控制系统至关重要。文献[7]利用龙伯格观测器设计了系统扩张状态观测器，对汽车发动机的转速等参数进行了有效估计，从而实现发动机转速的有效控制。针对自动驾驶车辆环境感知问题，文献[5]采用最小二乘方法对车道曲率参数进行了数值估计。文献[3]采用带遗忘因子递推最小二乘法对自动驾驶汽车行驶过程中的附着系数和滑动率以及相关运动学参数进行了在线估计。文献[4]分别采用扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）和双UKF 方法对智能车辆的状态信息进行了估计。上述方法虽取得了一定成效，但仍有值得商榷之处。传统观测器方法通常要求输入信号满足持续激励条件，以保证待估计参数收敛，且存在着时间延迟的问题。而最小二乘方法、神经网络方法以及卡尔曼滤波算法对于参数初始值的选取则异常敏感，初始参数选择不当致使模型产生超调甚至失稳的问题，需要复杂的优化算法筛选初始值，不便于在线使用。针对上述问题，提出了一种有限时间收敛的自动驾驶车辆自适应参数估计方法。所提方法采用一阶滤波实现系统信号降噪，利用并行学习技术放宽了自适应观测器收敛的持续激励条件，并基于有限时间收敛理论设计了汽车质量以及路况信息的参数更新律，以期获得更高的收敛速度与稳定性。

2 行驶车辆力学分析

对于自动驾驶车辆，对其主要受力情况进行动力学分析，如图1 所示。

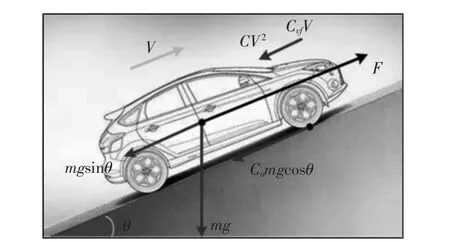
图1 行驶车辆的受力分析图Fig.1 Force Analysis Diagram of Moving Vehicle

由图1 分析可知，车辆在行驶过程中主要受到自身重力、动力装置牵引力、轮胎与地面接触产生的抓地力以及快速行驶所带来的风阻力。根据牛顿第二定律，其纵向运动方程如下[7-8]：

针对上述自动驾驶车辆的未知参数估计问题，将行进参数有限时间估计方法详述如下。

3 行进参数有限时间估计方法

3.1 低通滤波

采用低通滤波思想，引入下列车辆状态变量及回归向量的一阶滤波变量：

3.2 直接参数估计误差构建

根据上述推导，定义以下辅助回归矩阵Wcl（t）和辅助向量Fcl（t）：

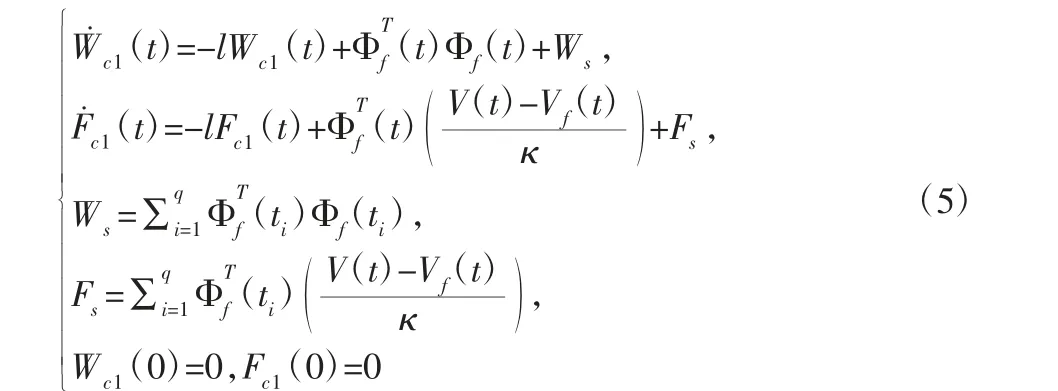
式中：l＞0—待设计参数，表示参数的衰减速率；Wcl（t）、Fcl（t）—回归矩阵和向量表达式，其中包含了当前时刻的数据和历史数据，即并行学习[10-11]。Ws和Fs为历史数据所构建的对应回归矩阵/向量。由式（5）可知：

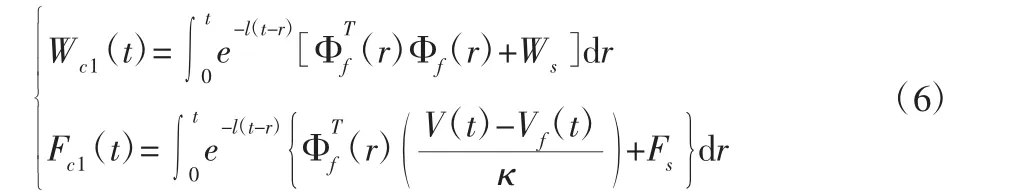
式中：参数估计误差向量定义为δ～=δ-δ^。

3.3 参数估计律设计

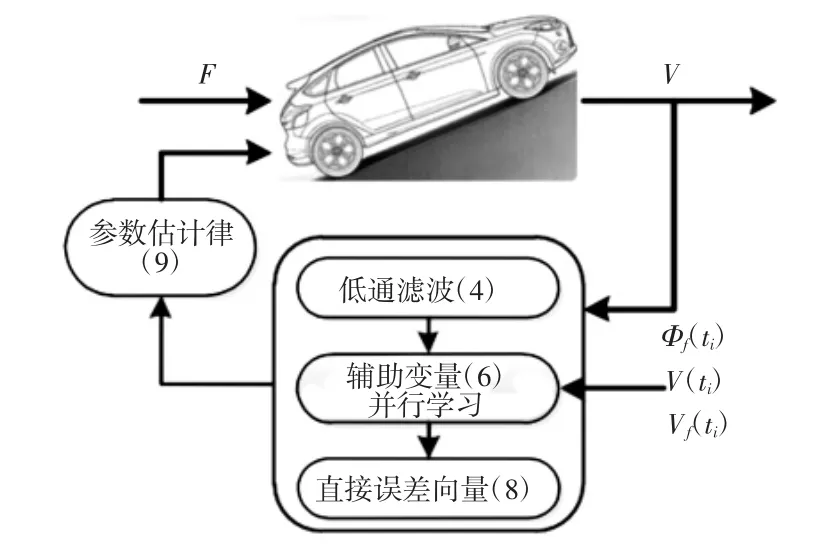
图2 所设计方法概览Fig.2 Full Scope of the Proposed Method

根据梯度下降规则，可设计参数估计律如下：

其中，Γ=Γ＞0∈R—增益矩阵，表征参数估计的更新速率。对比式（7）和式（8）可见，上述参数估计律直接由参数估计误差直接驱动故障估计过程，这与常规状态跟踪误差驱动的间接方式截然不同，突出了所设计方法的优势所在。为便于读者对所设计方法具有整体直观地理解，特给出这里方法的框架图，如图2 所示。

4 稳定性分析

为从理论上给出这里方法的收敛性证明，利用李雅普诺夫稳定性理论分析如下。

定理1 对于动态行进车辆（1），若满足条件1，则所设计参数估计律（8）能够保证未知参数误差向量δ～的全局有限时间收敛。

通过并行学习技术放宽了参数估计的持续激励条件，无需向系统注入激励信号。简化了系统设计途径，节省了系统运行成本，优化了参数估计效果，这将在仿真部分得以验证。

5 仿真分析

为验证所提方法的有效性，采用Matlab/Simulink 平台在PC机上进行仿真实验，引入某型号车辆的参数，如表1 所示。参数更新律（9）的相关设计值给定为：Γ=10I5，I5为5 阶单位矩阵，l=1，κ=0.001，q=10。为说明这里方法在非持续激励条件下的仿真效果，车辆动力F 选取为阶跃信号（阶跃信号为一种非持续激励信号）[13]。这里方法对车辆本身参数的仿真结果，如图3 所示。

表1 车辆行驶参数Tab.1 Vehicle Driving Parameters

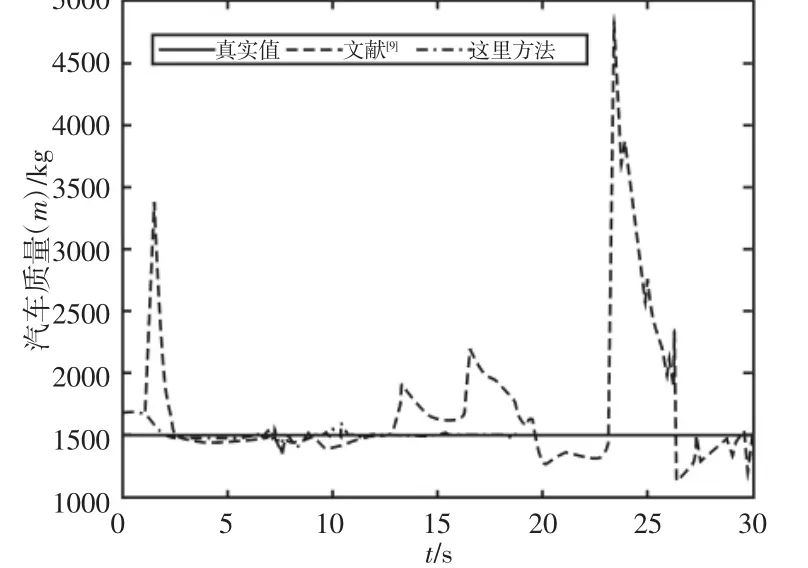
图3 行进车辆质量估计Fig.3 Estimation of Mass of Moving Vehicle

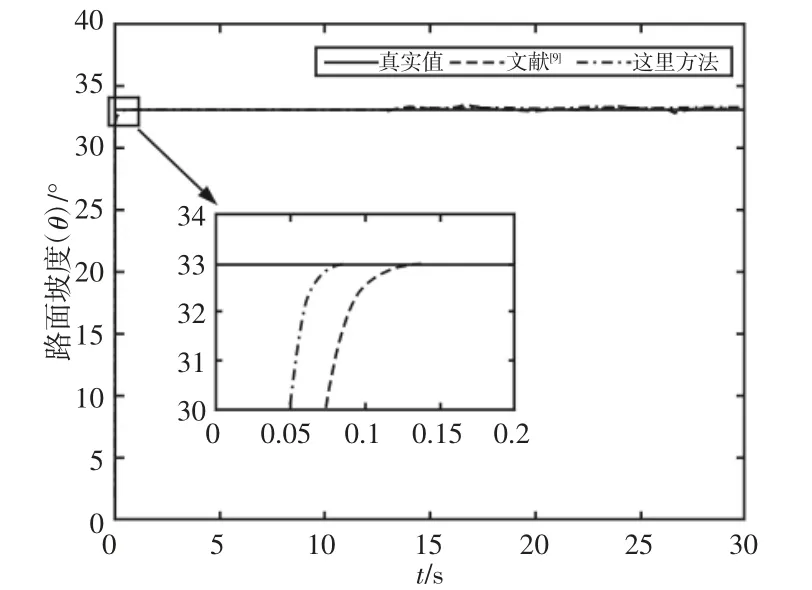
图4 路面坡度估计Fig.4 Estimation of Road Slope

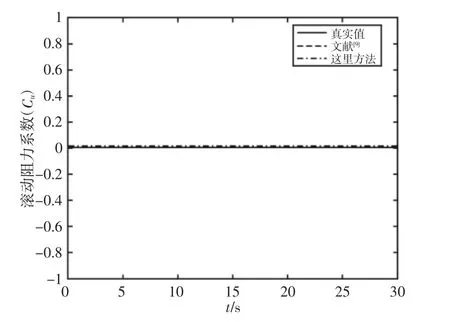
图5 轮胎滚动阻力系数估计Fig.5 Estimation of Rolling Friction Coefficient

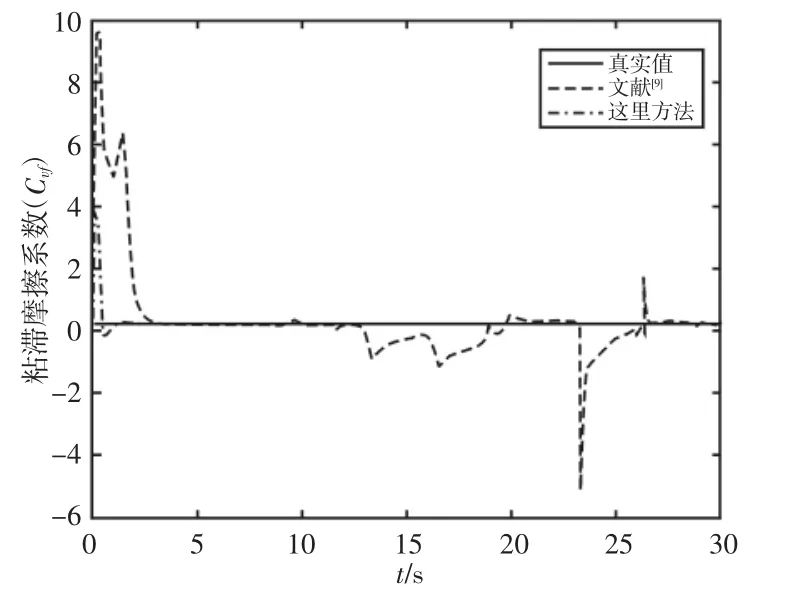
图6 粘滞摩擦系数估计Fig.6 Estimation of Viscous Friction Coefficient

观察图3 可知，所提方法能够实现行进车辆质量的快速、高效估计。对比文献[9]的方法，这里方法在参数收敛之后，仍能够保证估计结果的持续一致收敛，估计效果稳定性好。该收敛效果在后续仿真结果图中也得到了相应体现。对于路况信息的估计结果，如图4～图7 所示。

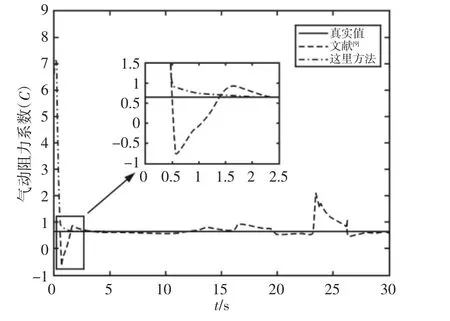
图7 气动阻力系数估计Fig.7 Estimation of Air Drag Coefficient

由图4 可知，这里方法能够快速、准确地估计路面坡度，收敛时间＜0.1s，充分体现了有限时间估计算法的优势所在。对比现有方法，这里方法有效提升了快速性，其原因将在后续仿真结果中进行详细解释。

由于车辆抓地力来自于强劲的动力总成和轮胎的良好维护，故轮胎滚动阻力系数相对较小。观察图5 可知，这里方法能够对其实现有效估计。

由于空气粘滞对行进车辆的动力学特性影响较大，故对其进行在线估计尤为重要。从图6 可以看出，在估计初期，曲线存在较大振荡，但很快就实现了有效收敛。特别地，若将存在参数突变的路况估计结果反馈给自动驾驶系统，将会带来不可估量的灾难。对比现有方法，这里方法在参数收敛之后，不存在未知突变，表现较佳，更为稳定、可靠。

空气对车辆行进带来的不仅是空气粘滞效应，更重要的是形成了气动阻力，这也是车辆（或跑车）多设计成流线型或近流线型的原因所在。观察图7 可知，气动阻力系数C 的估计结果在初期也存在与Cvf估计类似的大幅振荡情形，但从局部放大图可以看出，所提方法能够在一次振荡后快速收敛，收敛效果快又稳，进一步验证了其优越性能。

根据参数更新律的稳定性证明式（12）可知，系统激励水平σ 决定了参数更新的收敛速率，激励水平越高，则参数收敛越快。由于并行学习技术加持，这里方法能够在整个估计过程中始终保持其激励水平，从而确保了参数收敛的快速、准确、可靠，如图8所示。而对比现有方法，由于系统在初始激励之后不再持续激励，其激励水平呈现持续下滑趋势，这也是其在估计后期无法保证参数更新持续稳定的根本原因。

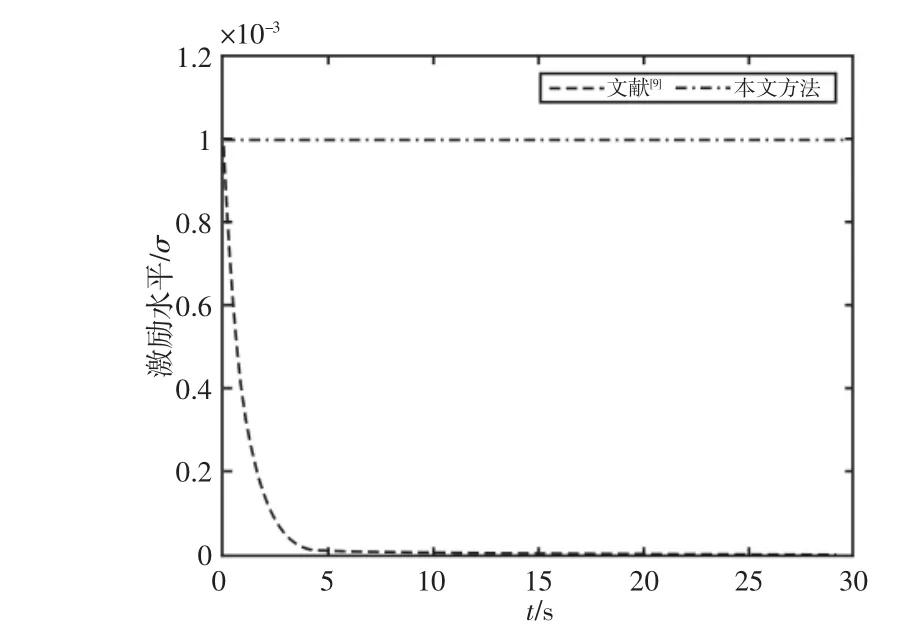
图8 激励水平Fig.8 Excitation Level

进一步观察图9 可知，这里方法在历史数据筛选方面也能够做到快速、稳定。在初期激励之后，就形成了稳定的回归向量历史数据矩阵集合，保证了条件1 成立，确保了参数更新的持续激励。

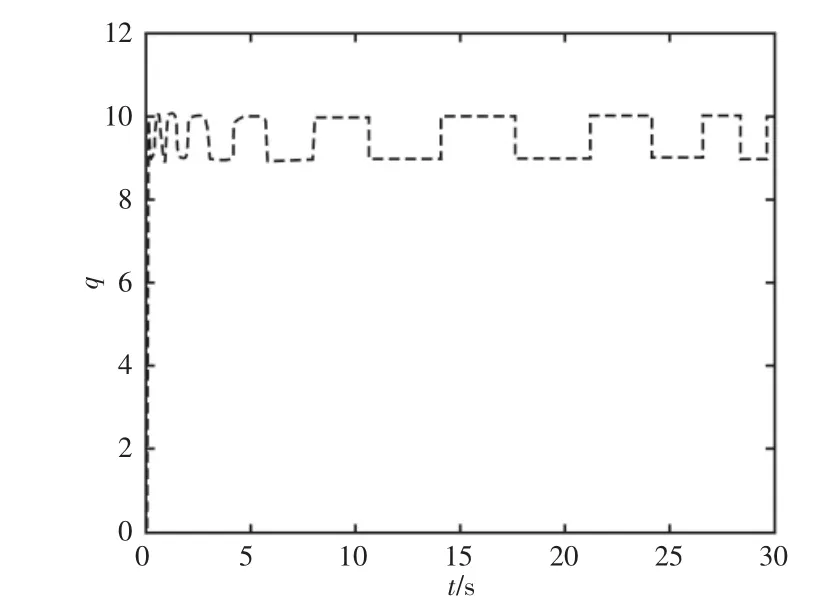
图9 存储数据更新次数Fig.9 Iteration Time of Stored Data

6 结论

针对自动驾驶车辆行驶过程中车辆和路况信息估计存在问题，结合并行学习技术，提出了一种有限时间自适应参数估计方法，并通过仿真验证得到以下结论：

（1）通过构建辨识参数的仿射参数模型，推导了参数估计误差向量，并基于有限时间收敛理论设计自适应参数的更新律。

（2）研究结果表明，所提方法能够对行驶车辆和路况信息进行及时有效地估计，且收敛速度快，更加稳定、可靠。同时，与现有方法相比，本方法放宽了持续激励条件，更适合车辆行驶过程中参数的实时变化，有利于系统长时间安全可靠地运行。