基于蚁群算法的共享快递盒配送回收网络优化研究

牟能冶，贾程方，康秋萍，龚 迪

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756）

0 引 言

随着环境污染和资源浪费问题在物流业日益凸显，各大电商企业开始采取措施促进快递包装的“绿色化”，共享快递盒作为绿色包装的产物应运而生[1]。然而回收情况并不理想，原因一是客户的配合意愿不够强烈且影响快递员的工作效率，二是回收成本高昂[2]。因此，通过对配送回收网络进行路径优化，从而提高企业的回收效率，加速共享快递盒的循环使用，以及降低企业的运作成本成为当前亟须解决的问题。

同时取送货问题（VRPSPD）是经典车辆路径问题（VRP）的一种扩展，该问题由Min 于1989年首次提出[3]，随着应用背景和适用范围的深入，使得研究更加贴近实际。Liu 等[4]针对家庭医疗物流领域构建了带时间窗的VRPSPD 模型；陆志强等[5]针对航空领域构建了飞机移动生产线物料配送与空箱回收集成决策模型；陈俊[6]针对汽车领域构建零部件供应和回收双向物流路径优化模型。与此同时，学者们针对实际情况考虑不同的因素，孙青伟等[7]考虑集成物流概念下构建了同时取送货的选址-多车型路径模型；赵燕伟等[8]构建了以碳排放最小为目标的多车型 VPRSPD模型；Shimizu 等[9]考虑了装载重量影响下的多仓库路径优化问题；马艳芳等[10]构建了以总成本最小为目标的低碳环境与模糊需求下的同时取送货模型；张涛等[11]构建了以总行程最小的逆向同时取送货模型。由于VRPSPD 问题属于NP-hard问题，所以多采用粒子群算法[12]、蚁群算法[13]、离散布谷鸟算法[14]、自适应并行遗传算法[15]、改进的迭代局部搜索算法[16]、模拟退火算法[17]、离散差分进化算法[18]等启发式算法进行求解。

综上所述，VRPSPD 问题研究丰富，但是考虑因素较为单一，且大多以成本、路程等单目标进行优化。而本文根据共享快递盒实际运作中存在的成本高昂和工作量分配不均等问题，考虑到配送与回收的不确定性、时间窗，构建同时配送与回收的多目标路径优化模型，引入等待时间因素设计蚁群算法的转移规则并求解，通过仿真实验验证模型和算法的有效性。

1 数学模型

1.1 问题描述

本文的问题可具体描述为：车辆从确定的分拨中心出发，对各快递站点所属的快递件进行相应的配送，并同时将自营的快递站点、第三方快递点的共享快递盒进行回收，直至车辆完成所在路径的配送和回收，接着返回回收检测中心卸载回收到的所有损坏的共享快递盒，并将完好的返回分拨中心进行下一次调拨。由于整个配送回收网络是基于自营的角度，且存在客户需求、配送与回收的不确定性，因此自营快递站点的配送量和回收量均为不确定需求。而第三方快递点的配送由第三方物流完成，因此，在该网络下的配送量为0，同时需要负责回收第三方快递站点的共享快递盒，且回收量不确定。该问题的结构如图1 所示。

图1 共享快递盒的配送回收网络优化

1.2 模型假设

（1）共享快递盒配送回收网络的分拨中心、快递站点和回收检测中心的位置已知，即分拨中心到快递站点、快递站点到快递站点、快递站点到回收检测中心的距离已知。

（2）共享快递盒分拨中心是所有路径的起点和终点，所有车辆均从分拨中心出发，完成配送和回收任务后先到回收检测中心卸损坏的共享快递盒，再返回分拨中心。

（3）本文考虑一种车型，且车辆数量足够多，其最大载重量、最长行驶距离、单次使用的固定成本已知。

（4）本文考虑使用的共享快递盒为同一型号，且损坏率已知。

（5）所有的快递站点均被服务，且每一个快递站点只能被一辆车服务一次，同时全部快递站点对回收的共享快递盒具有好坏识别作用。

（6）本文考虑早到与晚到的单位惩罚成本相同，运输成本与运输距离成正比。

（7）在配送回收过程中，不考虑突发状况的影响。

1.3 符号定义

1.4 多目标优化模型

本文从降低运作成本和平衡员工工作量两个角度出发，考虑不确定需求的、带时间窗的、同时配送与回收问题（Vehicle Routing Problem with Simultaneous Pickup and Delivery、Time Window and Fuzzy Demand，简称VRPSPDTWFD），具体建模如下：

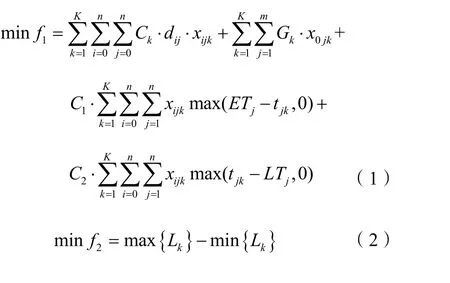
s.t.

目标函数（1）表示共享快递盒配送回收网络路径规划的总成本最小；目标函数（2）表示最小化最长行驶距离和最短行驶路径的距离差，从而平衡工作量；公式（3）与（4）表示车辆从共享快递盒分拨中心出发，且从回收检测中心回到分拨中心；公式（5）表示车辆行驶至路径节点j 后必须从此节点驶出；公式（6）表示一个快递站点或者回收检测中心只被一辆车服务，且只能被服务一次；公式（7）表示从分拨中心发出的共享快递盒的总装载量不超过车辆的最大容量；公式（8）表示在到回收检测中心前的子路径下回收的共享快递盒的总量不超过车辆的最大容量；公式（9）表示车辆行驶至任意节点j 的共享快递盒的装载量不超过车辆的最大容量；公式（10）表示车辆k 由i 到j 但还未开始给j 服务时的装载量；公式（11）表示车辆k 行驶的路径总长度，公式（12）表示车辆的行驶路径总长度不超过该车辆的最大行驶里程；公式（13）表示车辆k 行驶到任意节点i 的累计距离不超过车辆的最大行驶里程；公式（14）表示车辆到达j 的时间，公式（15）表示整数约束。

1.5 模糊约束处理

本文对不确定环境下带时间窗的共享快递盒配送回收车辆路径优化问题构建了含有模糊变量的多目标数学规划模型，包括配送量和回收量这两个模糊变量。因此，本文拟用机会约束规划方法对带模糊变量的约束条件进行处理。

因此，根据上述定义，易将模糊机会约束条件（7）、（8）、（9）、（10）转化为与之对应的等价约束，如下所示：

1.6 多目标转化为单目标

本文考虑的两个目标函数分别为配送回收网络路径规划的总成本最小和最长最短路径距离差最小化，其量纲不一致，因此，需通过无量纲和线性加权处理转化为单目标问题：

式中，1β ，2β 为权重系数，其大小取决于两个目标的重要程度。

2 蚁群算法设计

2.1 路径的构造

本文考虑了各快递点可接受服务的时间窗，因此，在蚂蚁的转移过程中会优先服务时间窗较短的快递点并且缩短车辆访问各快递点时的等待时间，因此，将等待时间waitj这一因素考虑进转移概率，waitj具体表达式如下：

因此，蚂蚁k 从快递点i 转移到快递点j 的转移规则如下式所示：

2.2 信息素的更新

本文在蚁群算法求解过程中，采用全局信息素更新规则，ijτ 更新规则如下式所示：

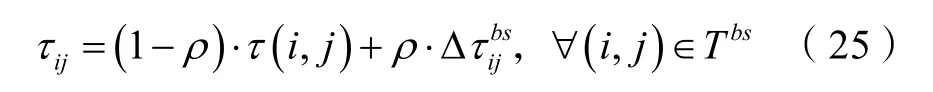
针对信息素释放的问题，本文采用ant cycle system 模型，具体表示如下：

式中，Q 代表常数，指蚂蚁循环一次释放的信息素总量； fpbest 指的是第k 只蚂蚁经过路径所得到的最优成本。

2.3 蚁群算法流程

利用蚁群算法求解共享快递盒配送回收网络模型的具体算法流程描述如下：

Step1 读取快递点相关数据，包括需求量、回收量、时间窗、服务时间、各节点间的距离，并初始化相关参数，此时迭代步数N =1 ；

Step2 将m 只蚂蚁随机放置到各快递节点；

Step3 对于每个蚂蚁k （k =1,2,3, …,m），根据转移概率规则计算蚂蚁k 的下一访问节点j，直到蚂蚁访问完所有节点；

Step4 计算每条完整路径的长度kL 、总成本F1、总固定成本CT1、总行驶成本CT2、总惩罚成本CT3、总行驶时间CT4，并记录当前迭代次数的最优值fpbest；

Step5 同时，按照全局式信息素更新规则更新全局信息素矩阵；

Step6 若迭代次数达到Nmax，则跳到Step7，否则清空ijτΔ ， N =N+1 ，跳转到Step2；

Step7 输出最优解。

3 算例分析

3.1 算例背景及基础数据

以苏宁成都某片区的共享快递盒配送回收网络为基础，进行模型的仿真求解分析。网络中有一个共享快递盒分拨中心，其地址坐标为（104.187 638，30.560 487），分拨中心的开启和关闭时刻为（6，20），假设分拨中心各配送车辆车型一致，车辆信息如表1 所示。网络中只有一个回收检测中心，地址坐标为（104.226 985，30.503 652），服务时间窗为（8，18），服务时间为0.5h。该网络中需要服务的客户即快递点共有31 个，包括19 个苏宁自营快递点和12 个第三方快递点，其中，分拨中心、检测中心以及31 个快递节点的编号依次为0，1，2，…，32，故分拨中心在程序中表达的节点是0，回收检测中心为1，快递节点的编号是从2 开始，依次类推，31 个快递站点的地址信息如表2 所示。

表1 车辆相关参数

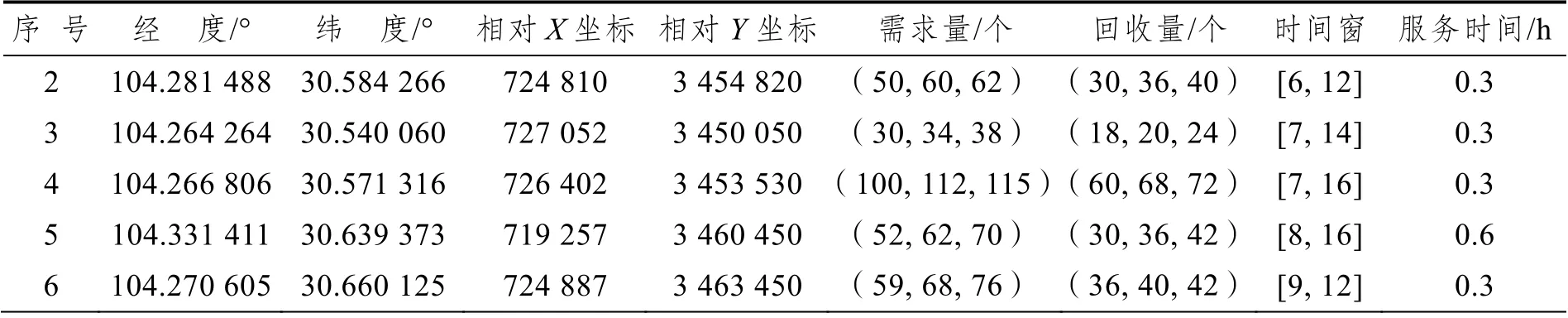
表2 快递站点信息

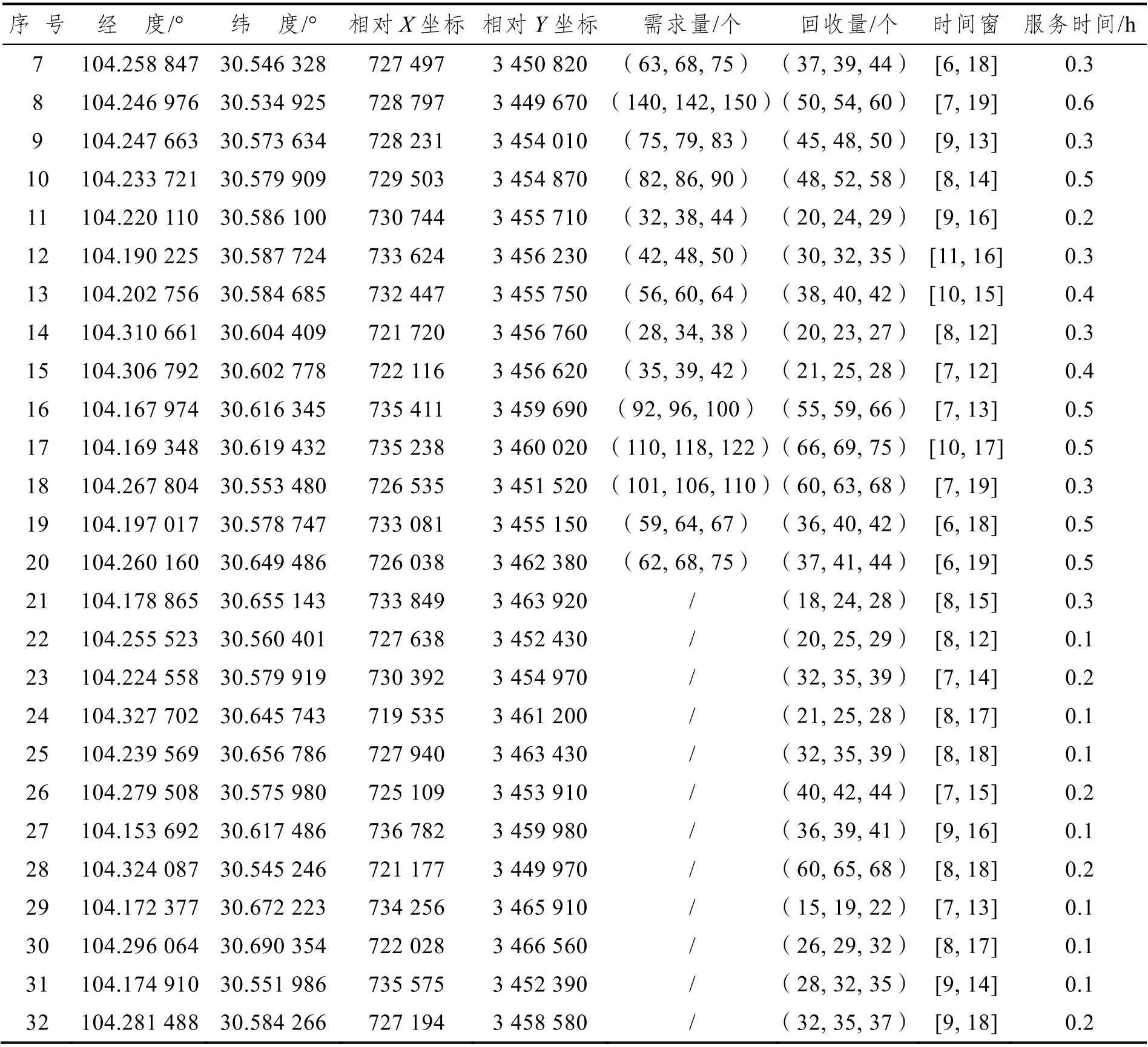
续表2

对市场进行调查分析，假设早于时间窗到达需要等待的单位惩罚成本 C1=10 ，晚于时间窗到达产生延误的单位惩罚成本 C2=10 。

3.2 算例求解

算法中相关参数设置如下：算法最大迭代步数Nmax=500，信息素重要程度因子α = 1，启发函数重要度因子β = 5，挥发系数ρ =0.2，控制参数 q0=0.2，信息素强度Q= 50，蚂蚁总数为50，需求和回收量的置信水平系数均取0.9，目标函数权重系数均取0.5。为兼顾算法稳定性和精确性，进行10 次仿真，并选取最优结果如图2、表3 所示。

图2 最优配送回收网络路径图

表3 最优配送回收网络路径决策

目前，共享快递盒的运作模式采用传统的正向配送与逆向回收分开进行，且配送针对自营快递站点，不需要返回回收检测中心，所以，分拨中心与19 个自营快递点的编号依次为0，1，2，…，19，其中，0 表示分拨中心，自营快递点的编号从1 开始，依次类推。多次仿真分析，选取最优的传统配送和回收路径方案，具体如图3、图4所示。

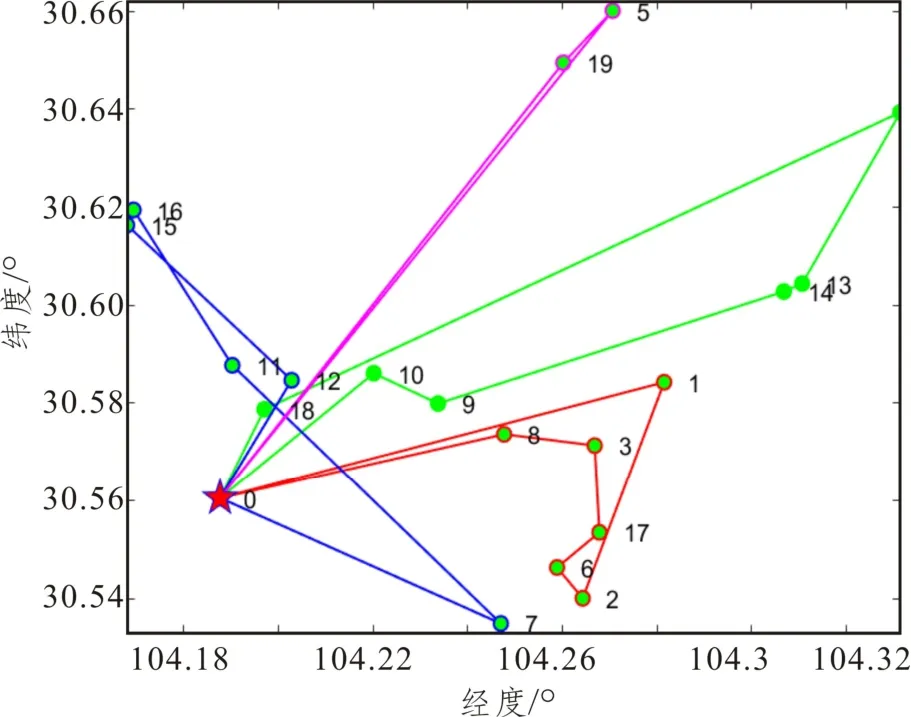
图3 最优配送方案路径图

图4 最优回收方案路径图

通过以上仿真分析，对同时配送回收模式和传统配送、传统回收模式两种方案进行对比，具体比较结果如表4 所示。

表4 两种模式的结果对比

由结果对比可知，同时配送与回收所需车辆数比传统配送、传统回收方案所需车辆数降低50%，极大提高了车辆的使用率；且行驶总距离降低43.6%，使得在同时配送与回收模式下的总成本降低45.9%，大幅度降低了企业的运作成本。此种模式下，配送与回收同时进行，可以加速共享快递盒的循环，且在快递站点进行回收的共享快递盒，给客户一定的时间进行返回，从而进一步提高回收的效率。并且同时配送与回收模式下，配送量与回收量更接近车辆的最大载货量，使得车辆空载率低，路径差也相对较小，员工的工作量也较平衡。

为分析决策者决策偏好对结果的影响，本文在同一实验数据下，分别选取不同的车辆载重量kQ 、单位惩罚成本C、目标权重系数1β 及2β 的值，比较不同决策对行驶距离kL 、总成本1f 、最长最短路径差 f2的影响，具体如图5、图6、图7所示。

图5 k、 f 1、L k 随Qk 变化趋势图

图6 k、 f1 随C 变化趋势图

由图5、图6 可知，车辆载重量kQ 和单位惩罚成本C 对总成本的影响明显，随着kQ 的增加，车辆数k 减少，车辆的行驶距离降低，总成本降低；而总成本与C 呈正相关，随着C 增加，且C= 40时，通过牺牲行驶距离，即先配送距离相对较远的快递点来减少惩罚成本的影响。

由图7 可知，随着1β 逐渐减小，2β 逐渐增大，最长最短路径差会减少，即快递员的工作量越来越平衡，总成本呈不断增加的趋势；但当2β 从0.4 增加到0.5 时，为了平衡工作量，所以会牺牲一定的运输距离，此时车辆数减少，固定成本降低，总成本会出现下降拐点，但此后总成本继续呈增加趋势。

图7 f 1、 f 2、 Lk 随 β1 及 β 2变化趋势图

4 结 论

本文针对共享快递盒实际运行模式的不足，在模型中考虑了需求与回收的不确定因素，从运作总成本最低和平衡员工工作量两个角度出发，构建了同时配送与回收共享快递盒的路径优化模型（VRPSPDTWFD），并设计改进的蚁群算法求解带时间窗的路径规划问题，通过算例验证了模型的合理性和算法的有效性。此外，算例表明，决策者的决策偏好对总成本和员工的工作量平衡影响明显，因此，在保证快递员合理工作量的前提下，尽量选择较大的载重量汽车，并采用较低的单位惩罚成本，可以有效降低网络运行的总成本；同时，相对平均的目标权重系数，可以保证整个网络运作成本和工作量差异的相对最优。

然而，本文在模型方面未考虑交通路网受路况变化以及突发状况的影响，同时，由于员工的工作量不仅包括行驶距离，也包括在各快递站点的等待时间、服务时间等，因此，在未来的研究中，可考虑动态交通路网，且使用时间因素来平衡员工之间的工作量。