基于双向BFS 算法的城市轨道交通有效路径研究

曾 诚，吴佳媛，罗无瑕，罗 霞

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756；3. 西南交通大学，公共管理与政法学院，成都 610031）

0 引 言

随着我国城市化与现代化进程的推进，城市规模不断扩大，轨道交通逐渐成为城市的大动脉。城市轨道交通具有大运能、高效率、安全可靠的特点，其中地铁的效用尤为显著。《“十三五”规划》指出，超大城市和特大城市应积极建设城市轨道网络，“十三五”期间共新增城市轨道交通运营里程3 000 km 以上。截至2019 年底，我国仍处于城市轨道交通建设发展的热潮，以成都市地铁运营现状为例，共计有7 条线路，207 座车站，运营里程位居全国第八，单日最高客流533 万人次，2020 年12 月18 日更是一次性开通5 条线路。

面对如此庞大的客流和日趋复杂的地铁网络，客流预测和客流清分等工作显得尤为重要。其中，有效路径的确定是上述实际工作的理论基础。如何计算出完备、无冗余的有效路径集是研究乘客出行选择行为[1-4]、客流预测[5]和客流清分[6]工作的第一步。

目前，用于城市轨道交通有效路径求解的算法主要包括Dial 算法、K 短路算法、深度优先算法、广度优先算法、基于定向树遍历搜索算法，以及各种启发式算法和改进算法等。其中，Dial首先提出了不考虑拥挤程度情况的有效路径求解算法，能有效解决交通网络随机分配问题，适用于大规模交通网络。但由于算法对有效路径的定义过于严格，导致关键路径识别阶段出现异常，且当网络中存在环形通路时，该算法也会遗漏部分路径[7,8]。四兵锋、张好智等针对上述问题对Dial 算法进行了改进，将路段费用信息作为判定有效路径的必要条件，提出了基于网络拓扑结构排序的模型算，并进一步验证了该算法的有效性，能够同时避免Dial 算法的有效路径遗漏问题和非有效路径的错误判别问题，但算法复杂度较高[9]。随后K 短路径搜索算法进入人们的视野，它由Hoffman 等在1959 年提出，能够有效搜索出最短、次短、第K 短路径[10]。其后一些学者提出了采用删边法的K 短路径搜索算法来求解有效路径，比传统的全路径法有了很大的提高，但是这种限定有效路径数目的方法并不能真正满足出行者路径选择范围的要求[11]。如牛新奇等提出的基于Dijkstra 算法的K 短路搜索仅适用于小规模网络，限定有效路径数目后会遗漏部分路径[12]。叶晋、赵烈秋应用遗传算法求解轨道交通换乘路径，提出一种求解轨道交通K 条最佳换乘路径的遗传算法[13,14]。随着计算机计算能力的提高，全路径搜索算法得以应用。如毛保华运用深度优先遍历搜索算法求解有效路径，在该算法基础上提出了基于回溯遍历的搜索算法，即沿着图的一个分支搜索直到该分支终点，然后进行回溯遍历，在搜索过程中同时判断有效路径是否满足相对阀值和绝对阀值的定义[15]。刘剑锋等提出了一种基于分支定界思想的深度优先有效路径搜索算法，当路径费用大于出行路径广义费用最大阈值时，停止该条路径搜索[16]。郭彦云利用广度优先算法求解有效路径，针对枚举算法效率低的问题，采用了增加有效路径限制条件和定义关键节点的方法[17]。

综上所述，可将目前各类求解有效路径的算法中存在的缺点总结为四类：算法复杂、有效路径结果缺失、有效路径结果冗余或有效路径结果不合理。针对这种情况，本文充分利用城市轨道交通乘客的出行特征和网络特点，提出了一种基于广度优先算法的双向BFS（Breadth-First Search）算法来求解有效路径，并利用算例验证其有效性。

1 有效路径的定义与假设

1.1 有效路径定义

本文对有效路径的定义如下：在特定OD 对之间存在若干条可供乘客选择的路径，这些会被出行者考虑的路径我们称为有效路径，非有效路径的广义出行费用更大，且都不可能被乘客选择。由两点之间的有效路径组成的集合称之为有效路径集。

1.2 有效路径基本假设

考虑乘客的出行习惯和后文算法的需求，对满足有效路径的路线作如下假设：

（1）城市轨道交通中的每个车站节点、每个区间路段最多只能经过一次。

（2）乘客所能接受的换乘次数是有限的，一般不超过3 次。

（3）乘客在旅行过程中经过换乘站进入一条线路，就不会再次换入该线路。

（4）在同一线路上的OD 对，乘客只在该条线路上进行旅行。

2 城市轨道交通网络编号原则

2.1 线路编号原则

本文以成都轨道交通为研究对象，主要包含线路有地铁1 号线、2 号线、3 号线、4 号线和7号线。根据研究需要确定编号原则如下：

（1）地铁1～4 号线延续运营编号，并且省略7 号线环线以外的支线部分。

（2）由于7 号线为环线，所以当起点和终点都在环线上时，最优路径可能需要换乘，这与有效路径假设（4）矛盾。因此本文将7 号线重新划分为7A、7B、7C、7D 四条线路，划分站点分别为一品天下、驷马桥、成都东客站和太平园（分别对应图中节点1、3、5、7）。具体编号如图1所示。

图1 成都市地铁网络简化图

2.2 车站及区间编号原则

在对城市轨道交通车站进行标号时，采用基于相邻换乘站或终点站的标号方法进行次序化处理[18]。如图1 所示，编号1～14 为换乘站，编号15～22 为终点站，建模时用表示，k 为编号，l 为所属线路。设其他普通车站用符号表示，i、j 表示相邻的换乘站或终点站，k 为沿下行方向的车站编号，例如“西南交大站”可表示为。

在对城市轨道交通区间进行标号时，为了减少算法中车站和区间的递归求解，缩短求解时间，将城市轨道交通网络中区间按上下行依次编号，如图2 所示。

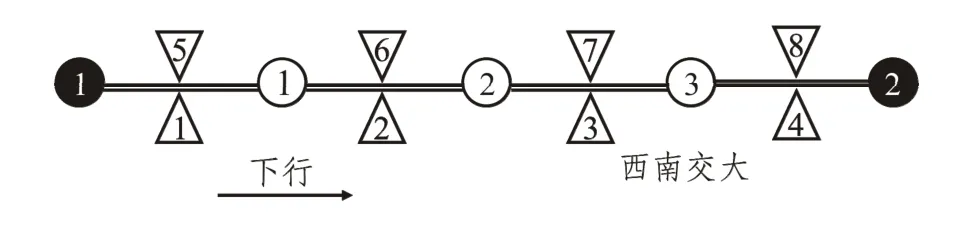
图2 路网的次序化编号

2.3 虚拟换乘区间编号原则

根据本文的线路编号原则，将7 号线环线划分为7A、7B、7C、7D 四条线路，因此当有效路径中包含上述站点并且换出线路与换入线路同为7M（M=A、B、C、D）号线时，实际上并没有换乘成本，需引入虚拟换乘弧的概念[18]，如图3 所示。

图3 换乘弧示意图

由上图可以看出，一个两线换乘站存在8 个换乘方向，可用换乘弧表示，“0”表示上行方向，“1”表示下行方向，则换乘弧（1，0）表示从一条线的下行方向换乘到另一条线的上行方向。当换乘站弧衔接的两条线实际是一条时，例如7A和7B 号线，则该换乘弧为虚拟换乘弧，虚拟换乘弧广义费用为0。

3 有效径路集求解算法

3.1 双向BFS 搜索算法简介

本文基于城市轨道交通的换乘特性，借用广度优先算法理念，设计了同时以O 点和D 点作为起始点的双向BFS 算法。

本文设计的双向BFS 搜索算法主要基于两个“乘客容忍度原则”（由调研获得）：一是乘客选择出行路径时换乘次数不超过3 次（否则选择其他交通方式）；二是从时间成本或广义成本上讲，所有有效路径的成本不超过最短路的（σ +1）倍。不同城市σ 的不同，如北京为0.15[19]，成都为0.25（由笔者通过问卷调查获得）。

3.2 网络拓扑建模

通过上一节对路网的分层次序化处理，将轨道交通路网转化为用有向连通图G=＜V , E ,T ＞来描述的轨道交通网络模型：

设有效路径所包含的有序区间集为C，其中实际运行区间有序集为X ，换乘区间有序集为Y 。给定任意起讫点，则起讫点间的有效路径满足以下条件：

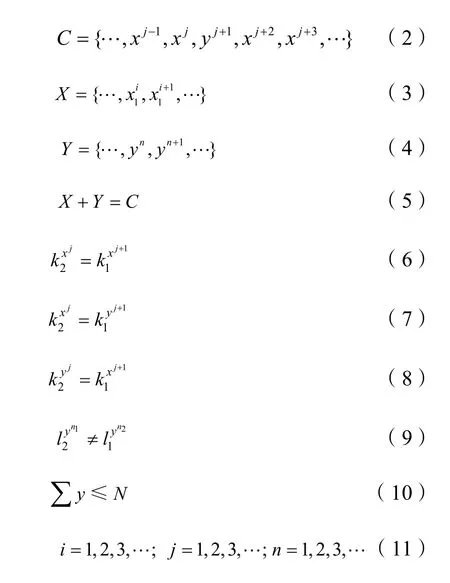
式中：j 为区间在集合C 中次序；i 为x 在集合X中的次序；n 为y 在集合Y 中的次序；1k 、 k2分别表示区间起、终点车站的编号；1l 、 l2分别表示换乘区间衔接的起、终点车站所属的线路。

式（6）保证有效径路在同一线路上的连续性；同理式（7）、（8）保证有效径路在换乘过程中实际区间与换乘区间的连续性；式（9）使有效径路满足基本假设（3）；式（10）限制换乘次数满足基本假设（2）。

3.3 算法步骤

由于乘客出行路径的选择行为可以描述为换乘站的不同选择，所以本文的双向BFS 算法以仅保留换乘站和终点站的简化路网为基础，从起点和终点同时利用检索相邻站的方法获得OD 之间的有效路径。双向BFS 搜索算法的具体步骤如下：

Step 1 初始化有效路径集W 、换乘站和终点站集合V 、邻接矩阵A、起始站点Ov 和目的站点 vD、相邻换乘站v1k与vk2之间的站点集合Vk1k2、线路-车站矩阵L、换乘矩阵H。

Step 2 检索站点 vO所在线路LO，检索站点vD所在线路LD，判断起讫点是否在同一条线路上，若是，则转入Step 5；若否，则继续。判断 vO、vD中是否存在换乘站或终点站，若是，则相邻站则为该站本身；若不是，则通过检索集合Vk1k2分别确定起讫点相邻的换乘站(p =1,2)、(q =1,2)。1 表示沿上行方向的换乘站，2 表示沿下行方向的换乘站。

Step 3 交叉判断起点的相邻换乘站与终点的相邻换乘站是否在同一条线路上。共需判断p × q组。若在，则找到一条有效路径O→→→D，并将其存入有效路径集W 。直到判断完所有相邻站组合，进入下一步。

Step 5 检索O、D 点的同线路非相邻换乘站（广义相邻站）。在O 点所在线路上按上行方向从开始检索换乘站，结果生成上行广义相邻站集合（集合包含）；同理生成下行广义相邻站集合（集合包含）。 D 点同理可生成上、下行广义相邻换乘站集合、。

Step 6 初始化m= 1，c 为W 中有效路径条数。从有效路径集W 中的第一条路径开始，判断是否同时存在集合、中的元素，或同时存在集合、中的元素，若有则说明存在重复路段，删除该路径。令m = m+ 1，当m ＞ c时，转入Step 7；否则，重复上述步骤。

Step 7 计算广义费用，令虚拟换乘弧广义费用为0，确定有效路径中最小出行成本wmin。通过比较其他路径与(σ +1)wmin的大小，剔除出行成本超过容忍度的路径。

Step 8 删除空白行，输出算法最终有效路径集合W ，算法结束。

算法流程图如图4 所示。

图4 双向BFS 算法流程图

Step 3 中由于算法规定了最大换乘次数为3次，所以当起讫点的相邻换乘站之间不在同一条线路时，想要搜索到有效路径必须找到一个换乘站 Ttran。该站既和O 点相邻站之一在同一条线路上，又和D 站相邻站之一在同一条线路上。

Step 6 中通过广义相邻换乘站删除包含重复路段的路径，该方法可以有效降低算法复杂度，避免了检索路径所有途经站点和区间的工作。

4 算例分析

本文以成都城市轨道交通网络为例，选取7号线茶店子站作为O 点，3 号线磨子桥站作为D点，如图5 所示。线路编号、换乘站编号按照前文所述进行编排，下面根据本文提出的“双向搜索算法”给出有效路径集的搜索过程。

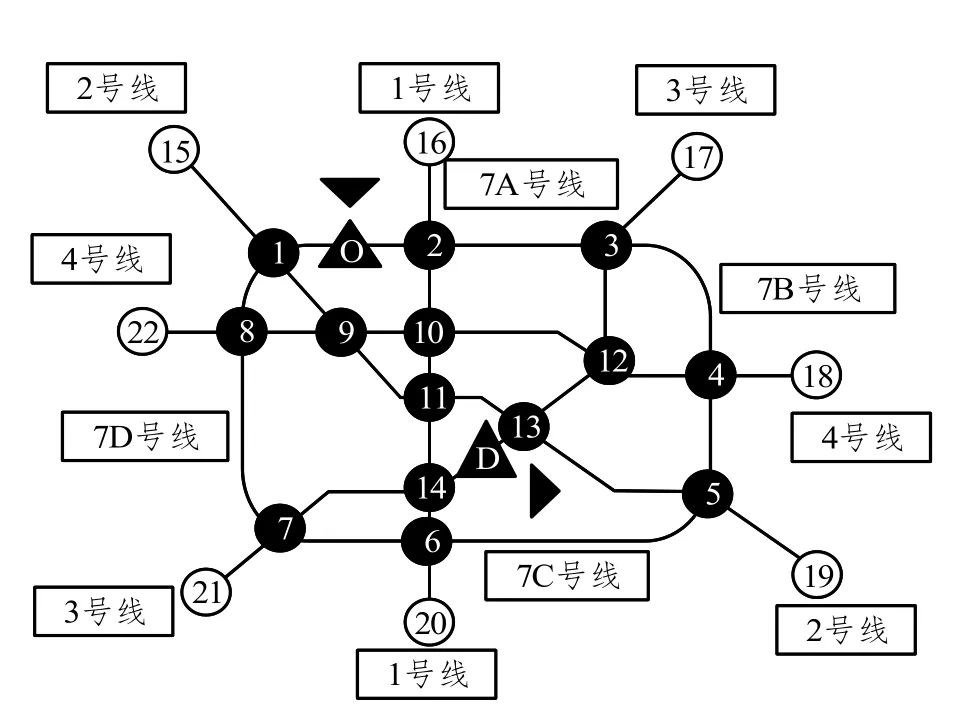
图5 OD 对示意图

第一步 初始化一系列必要参数。

第二步 分别确定O、D 点的相邻换乘站或终点站。根据线路和站点的从属关系，即车站—线路矩阵L，确定起点O 的相邻换乘站为1 和2，终点D 的相邻换乘站为13 和14。

第三步 分别确定各个相邻换乘站所在的线路。如换乘站1 从属于2 号线、7A 号线、7D号线。

第四步 交叉判断各相邻换乘站是否在同一条线路上。发现站点1 和14、站点2 和13 均不在同一条线路上，因此需要进一步搜索换乘站。站点1 和13 在都位于2 号线上，因此可以确定一条有效路径O→1→13→D；站点2 和14在都位于1 号线上，因此可以确定另一条有效路径O→2→14→D。

第五步 搜索包含3 次换乘的有效路径，搜索过程如表1 所示。

表1 包含三个换乘站的有效路径搜索

第六步 根据前文Step 5、Step 6 的方法，删除路径中包含重复区段的路径，得到最终有效路径集。本例共计6 条：

O→1→13→D

O→2→14→D

O→1→11→14→D

O→1→7→14→D

O→2→11→13→D

O→2→3→13→D

由于上述算法搜索得到的有效路径仍比较多，存在一些因出行成本相差较大，实际上不会被乘客选择的路径（城市轨道交通旅客考虑的路径往往只有1～3 条），因此本文用表示旅行时间，用nk换乘表示换乘次数，用表示换乘时间，其中k 表示r - s间的第k 条路径，提出如下的路径广义费用函数：

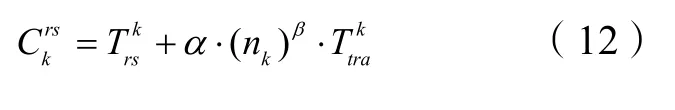
式中： α·( nk)β·为换乘费用，α 、β 为待定的参数。另外，基于有效路径成本不超过最短路（σ +1）倍的假设，定义σ 为容忍系数，本文根据一定量的出行路径选择调查，对模型中的参数进行标定，取值见表2。

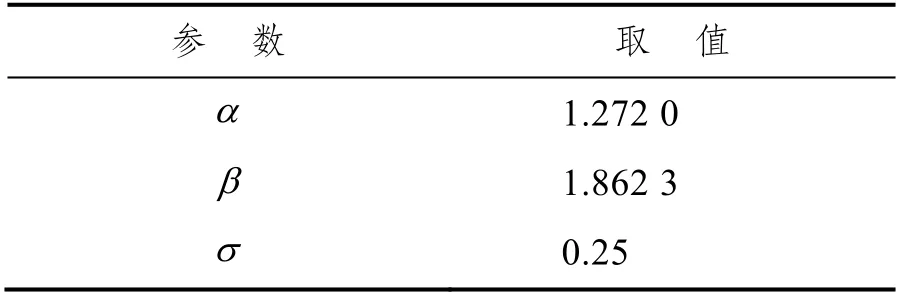
表2 模型参数的取值

根据前文筛选出的6 条有效路径计算每条路径的旅行时间、换乘时间和换乘次数，具体结果如表3 所示。

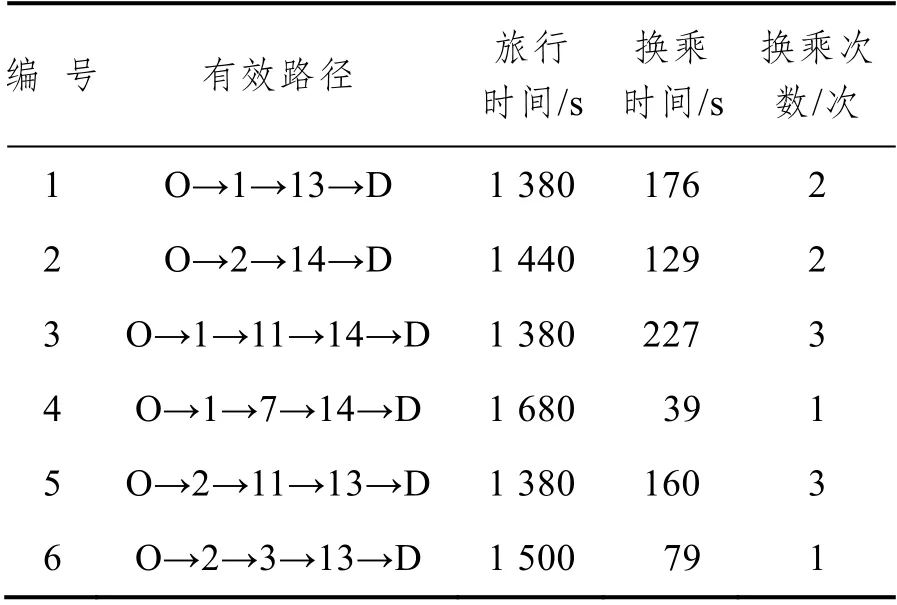
表3 六条路径的旅行时间、换乘时间和换乘次数

其中路径4 和6 由于包含虚拟换乘弧，因此实际换乘次数比经过的换乘站要少。接着，将上述指标带入概率模型中，分别得到广义费用值见表4。

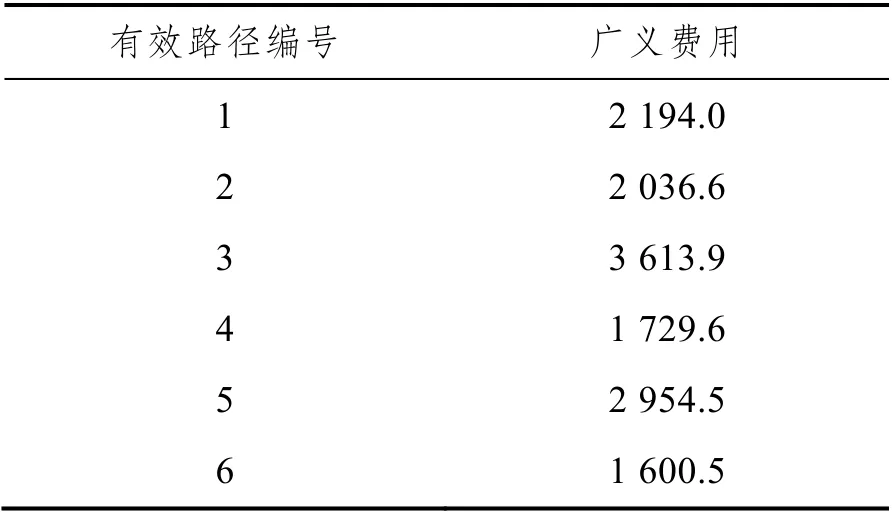
表4 有效路径广义费用

第七步 根据路径的容忍系数σ 剔除路径。经计算，广义费用最小的路径为有效路径6，其费用的1.25 倍为2 000.6，因此路径4 也可作为有效路径。最终确定茶店子站和磨子桥站之间的有效路径共两条，分别为O→1→7→14→D 和O→2→3→13→D。两条路径都只需要换乘一次，侧面反映出城市轨道交通旅客对换乘的敏感性。

改变OD 后进一步验算，结果见表5。

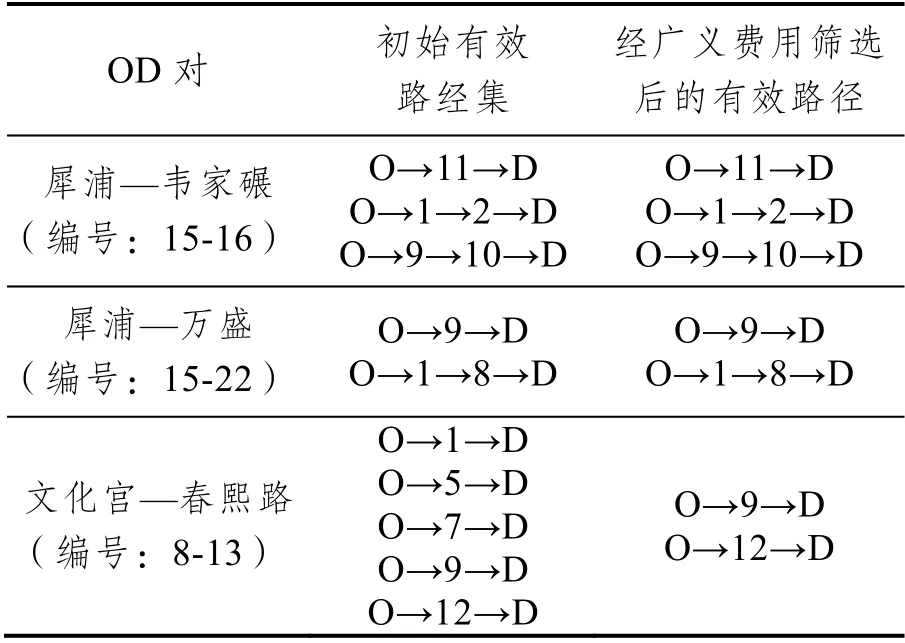
表5 其他OD 的算法结果

综上所述，本文的有效路径搜索算法很大程度上证明是完备和高效的。

5 结束语

本文设计的双向BFS 算法有如下优点：

（1）结合实际，结果完备。充分利用了城市轨道交通网络和出行者选择行为的特点，设定了换乘次数和广义费用的容忍阈值。路径搜索结果不存在冗余或不合理的有效路径，也不存在缺失的有效路径。

（2）逻辑清晰，设计巧妙。通过重新划分线路和定义虚拟换乘弧的概念，消除环线对求解的影响；从逻辑上巧妙地解决了双向搜索中路径交汇点的确定问题；并定义广义相邻换乘站快速删除包含重复路径的路径，避免了检索站点和区间的复杂计算。

（3）复杂度低，运算迅速。相比现有其他算法，本文算法对城市轨道交通网络的针对性更强，算法前期工作较多，因此输入数据较少。算法结构存在一定的对称性，执行每条指令所需的时间和语句重复次数都较少，所以运算速度上优势明显。具体运算时间与路网规模、路网复杂度、OD 点位置和计算机性能有关。