深圳市多层钢结构模块化幼儿园的抗震分析

赵宝军，王 琼，陈志河，黄少文，谭 健

（1、广东海龙建筑科技有限公司 珠海519000；2、深圳海龙建筑科技有限公司 深圳518110；3、南昌大学材料科学与工程学院 南昌330031）

0 引言

模块化建筑是一种集结构、建筑内装与外饰、机电、给排水与暖通等建筑全要素于一体，高度集成、新型高效的建筑形式。模块化集成建筑可以将90%以上的施工作业在工厂完成，现场只需完成吊装及处理模块拼接处的管线接驳及装饰等少量工作，现场施工免支模，减少现场施工工序，极大提高建造效率，缩短施工工期，是装配式建筑的最高形式，因而它具有一系列显著的技术优势及社会意义。

随着经济的发展和人口的大量流入，深圳市的教育设施供给不足、空间分布不均衡、优质教育资源短缺等问题日益凸显，且亟待解决。目前，深圳市福田区正在兴建8 座多层模块化钢结构幼儿园，通过利用模块化建筑的具有严格的质量保障，能实现快速建造的优越性，来解决福田区幼儿园教育资源供给不足的问题。

张鹏飞等人［1-2］针对多层钢结构模块化建筑和钢结构模块与钢框架复合结构体系，采用了模块单元插销螺栓连接节点，根据其传力路径提出了该节点的简化方式，并对简化方式的合理性进行了研究。杨晓杰［3］提出一种采用槽形截面钢作为模块梁柱的型钢模块建筑体系，该体系的模块之间采用高强度螺栓进行连接，并以一栋采用槽形截面钢作为主体结构构件的箱式模块化钢结构，考察了该种模块建筑体系的适用性。王炜［4］通过采用异形角柱与螺栓相结合的方式进行模块箱体与箱体之间的连接，并结合该连接形式对多层箱式模块化建筑进行了抗侧移刚度的理论分析。李若然［5］基于模块化钢结构的实际工程，模块之间的连接采用插销定位与模块角柱表面进行盖板螺栓连接结合的节点连接形式，对模块化钢结构建筑进行了结构静力分析，研究了模块结构的各项力学指标，提出了模块间连接节点的主要受力模式。邱韵［6］设计了一种“X 型”卡件节点用于连接多层集装箱式房屋外表面四相邻箱体，对其进行了数值模拟研究，并给出了节点简化等效弹簧模型。丁阳［7］从模块化结构层面和模块化建筑层面分别综述了国内外模块化钢结构建筑连接节点构造形式和研究现状。此前模块之间的节点连接多为插销螺栓连接，高强度螺栓连接，异形柱结合螺栓连接，插销式结合高强螺栓连接等形式。

这8座多层钢结构模块化幼儿园的模块之间均采用了新型的连接方式，即采用长螺杆结合带有抗剪连接锥的连接板相连接。因此结合其中1座幼儿园，对其结构进行抗震性能指标分析研究，并结合分析结果提出结构优化建议。

1 多层模块化钢结构信息

1.1 工程概况

本项目为3层钢结构模块化幼儿园，是由底层框架，第2、第3层为模块组成的钢框架结构体系。顶层楼梯模块顶面标高为14.65 m，设计使用年限50年，结构安全等级为二级。建筑面积2 709 m2。其2层建筑平面以及2层模块平面布置分别如图1、图2所示。

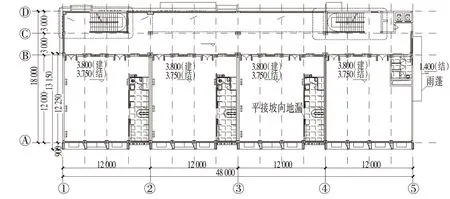
图1 幼儿园2层建筑平面Fig.1 Layout of the Second Floor of the Kindergarten

图2 幼儿园2层模块平面布置Fig.2 Layout of the Second Floor Module of the Kindergarten （mm）

本幼儿园为乙类建筑，根据《建筑抗震设计规范（2016年版）：GB 50011—2010》［8］的规定，其结构安全等级为一级，抗震等级为三级，抗震设防烈度为7 度，设计基本加速度为0.1 g。建筑物场地类别为Ⅱ类，场地特征周期为0.35 s，地面粗糙类别为C类。设计基准期为50年，基本风荷载标准值为0.75 N/m2。

1.2 建模信息

多层钢结构幼儿园底部框架柱为箱型柱，梁采用“H”型钢梁，第2、第3层模块化结构的梁柱均采用箱型截面。建模时楼板厚度设置为0，恒荷载按照考虑楼板实际重量输入，安装相邻模块之间的楼板相互独立。考虑到模块之间通过长螺杆结合带有抗剪连接锥的连接板相连接特点（见图3），实际建模时模块之间的连接简化成铰接的形式连接［9］（见图4），实际建模中为了安全考虑，模块水平连接则不进行铰接处理。幼儿园结构的主要构件信息如表1所示，主体结构如图5所示，盈建科分析模型如图6所示。

图3 新型连接方式示意图[8]Fig.3 Schematic Diagram of the New Connection Method［8］

图4 节点连接简化图［8］Fig.4 Schematic Diagram of the New Connection Method［8］

表1 结构主要构件信息Tab.1 Information of Main Structural Components

图5 幼儿园主体结构Fig.5 The Main Structure of the Kindergarten

1.3 结构初步计算

对该结构进行多遇地震作用下反应谱分析，可得其最大层间位移角为1/401，小于规范规定的1/250 的限值要求。结构第1、第2 振型均为平动，第3 振型为扭转，前三振型的自振周期分别为0.756 1 s，0.535 1 s和0.413 8 s，周期比为0.55。说明该结构满足抗震的基本要求。

图6 盈建科分析模型Fig.6 YJK Analysis Model

2 静力非线性分析

2.1 抗震性能化设计

根据结构的重要性等要求，在不同的地震作用下，对结构进行抗震分析，分析其是否达到规定的抗震性能化设计水准和性能目标。

实际分析中，结构的性能目标是否满足要求，通常由结构的层间位移角进行判断。根据文献［8］的规定，结构构件实现抗震性能要求对应的层间位移角限值如表2所示。

表2 结构构件实现抗震性能要求对应层间位移限值Tab.2 Inter-story Displacement Limits Corresponding to the Requirements of Structural Members to Achieve Seismic Performance

由于本项目为幼儿园，结构重要等级为乙类，本文分析设定的性能指标为性能2，即结构在多遇地震作用下，结构保持完好，结构的层间位移角远小于弹性位移限值；在设防烈度地震作用下，结构基本完好，结构的层间位移角略大于弹性位移限值；在罕遇地震作用下，结构存在轻微的塑性变形，变形小于2倍的弹性位移限值。

2.2 静力弹塑性分析结果

采用倒三角形（分别沿X、Y 正方向）和等加速度的加载方式（分别沿X、Y 正方向）对结构进行静力非线性分析，其中X、Y 方向分别对应模型长边、短边方向。在4 种工况作用下，性能点［10］处层间剪力与层间位移角的分析结果如图7所示。

结构在罕遇地震作用下，4 种工况对应的性能点的最大层间剪力和最大层间位移角如表3所示。

图7 4种工况下层间剪力及位移角Fig.7 Interlayer Shear Force and Displacement Angle under Four Working Conditions

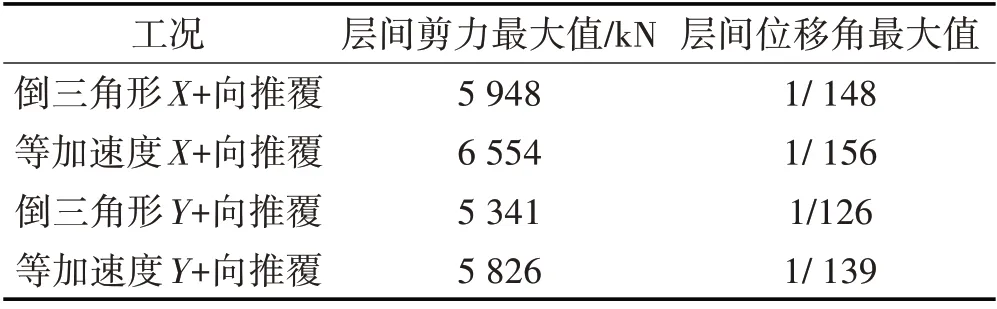
表3 4种工况作用下性能点处楼层最大响应Tab.3 Maximum Response of Floors at Performance Points under Four Working Conditions

在4 种工况作用下，静力弹塑性分析X 向和Y 向层间剪力的最大值分别为6 554 kN和5 826 kN。结构的最大层间位移角为1/126，小于表2中选定的性能2，即小于1/125。在罕遇地震作用且在同一加载方向的情况下，采用倒三角形加载方式均大于等加速度加载方式下产生的最大层间位移角。4 种工况作用下，在同一加载方向的情况下，采用倒三角形加载方式均小于等加速度加载方式下产生的最大层间剪力。由此可知，加载方式的不同对所分析的结构在罕遇地震作用下的响应影响较大。

2.3 构件性能化状态统计

本文分析中，梁柱的滞回曲线采用软件默认的滞回曲线，梁柱的从应力强化到出现塑性铰直至最终破坏期间的梁柱构件性能状态统计如图8所示。

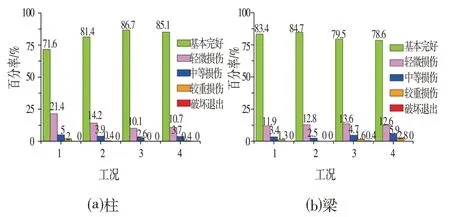
图8 柱构件性能状态统计Fig.8 Column Member Performance Status Statistics

由分析可知，在罕遇地震作用下，构件性能状态为“基本完好”，则未出现塑性铰，其余性能状态均为已出现塑性铰，出现塑性铰情况的构件大部分的性能状态为轻微损伤。由4种工况下构件性能状态统计情况可知，只有在倒三角形Y+向推覆的情况下，出现了极少数梁破坏退出工作的情况；在X+向推覆加载的情况下，结构的柱先于梁进入塑性铰状态，在Y+向推覆加载的情况下，结构的梁则先于柱进入塑性铰状态。

3 弹塑性时程分析

弹塑性时程分析方法是将特定的地震动输入结构中加以分析，求得在地面加速度随时间变化期间内，结构因地震波的输入所产生响应的全过程。

本文根据所分析结构以及文献［8］要求，选用了2条自然波（Coyote Lake波、Coalinga-01波）和1条人工波对本结构进行弹塑性时程分析。罕遇地震作用下，3 条地震波所对应的层剪力和层间位移角如图9～图10所示，分析结果如表4所示。

图9 地震波作用下层间剪力最大值Fig.9 The Maximum Interlayer Shear Force under the Action of Seismic Waves

图10 地震波作用下层间位移角最大值Fig.10 The Maximum Value of the Interlayer Displacement Angleunder the Action of Seismic Waves

表4 结构在3条地震波作用下楼层的最大响应Tab.4 The Maximum Response of the Structure under the Action of 3 Seismic Waves

由分析可知，罕遇地震作用下，弹塑性时程分析X向和Y向层间剪力的最大值分别为4 771 kN和4 125 kN。罕遇地震作用下，X、Y 分别为主方向时弹塑性时程分析所得的层间位移角最大值分别为1/61 和1/56，均满足规范规定的1/50的限值要求。

4 总结

⑴静力弹塑性分析时，不同的加载方式对最终的分析结果有所不同。倒三角加载方式下的多层钢结构模块化建筑的首层剪力小于等加速度加载方式下的首层剪力。同时层间位移角则同样小于等加速度加载方式下的层间位移角。

⑵静力弹塑性分析时，结构的层间位移角满足在罕遇地震作用下，结构存在轻微的塑性变形，变形小于2 倍的弹性位移限值要求。弹塑性时程分析时，结构的层间位移角满足弹塑性层间位移不应大于层高的1/50的限值要求。

⑶静力弹塑性分析时，结构构件大部分未进入屈服状态，且极少数梁出现破坏退出工作的情况，说明大部分构件的性能储备较大。在X+向推覆加载作用下，柱先于梁进入塑性铰状态，说明X 方向的柱强度小于梁的强度，因此结合大部分构件性能储备较大的情况，可适当减少构件截面尺寸，且构件截面减少后需保证满足“强柱弱梁”要求。

⑷通过本文的分析结果，验证了采用新型连接节点的此类多层钢结构模块化建筑体系合理性。因此，将此类具有绿色节能、高品质、高建造效率等一系列显著的技术优势的多层钢结构模块化建筑推广应用于学校教育设施建设，应急防疫类医院等的快速建造有着巨大的社会效益。