基于构件变形的RC框架-剪力墙结构地震损失评估方法研究

2021-06-05郑宜，曹源

广东土木与建筑 2021年5期

郑宜，曹源

（1、广东城建达设计院有限公司广东佛山528200；2、华南理工大学建筑设计研究院有限公司广州510640）

随着基于性能的抗震设计方法［1］的不断完善，大震造成的建筑物倒塌和人员伤亡得到了有效的控制，但带来的经济损失却难以估量。为解决这一问题，Cornell 等人［2］提出了以全概率理论为基础的新一代性能化设计方法，考虑了地震过程的各种不确定性。美国太平洋研究中心以此为基础，提出了新一代性能化设计方法的框架，即PEER-PBEE［3］方法。Ramiresz［4］、Shokrabadi［5］、Martins［6］等人基于蒙特卡洛算法对PEER-PBEE 方法进行简化，使其便于实际应用。美国联邦应急管理署FEMA于2012年发布了FE⁃MA-P58［7］，是下一代性能化设计方法的高度总结。

国内不少学者也对建筑结构的地震经济损失展开了研究。曾翔等人［8］利用FEMA-P58方法预测了3栋典型框架的地震损失。李星军［9］基于PEER-PBEE 方法评估了框架的抗震性能，并计算了加固方案的投资收益率。罗文文等人［10］对不同设防烈度的RC 框架进行地震损失评估，分析表明各烈度区建筑的地震损失风险不一致。韩建平等人［11］计算了框架-填充墙结构的地震损失，结果表明不考虑填充墙的建模方式将高估结构的地震损失。

从国内外的研究现状发现，大多数地震损失的研究都是以框架结构作为对象，而对于实际工程中广泛存在的框架-剪力墙结构涉及较少。再者，FEMA P-58方法存在一定的局限性：采用层间位移角作为结构构件损伤状态的识别参数，并不能准确判断构件破坏状态。因此，本文基于构件变形提出一种地震损失评估方法，并采用该方法进行框架-剪力墙结构的评估。

1 地震损失评估方法的建立

1.1 地震损失评估理论

地震经济损失评估最直观的结果为损失的年平均超越概率曲线。为得到该曲线，需先得到E［L|IM］，即地震强度为IM 时的地震损失，计算方法如式⑴、式⑵所示。

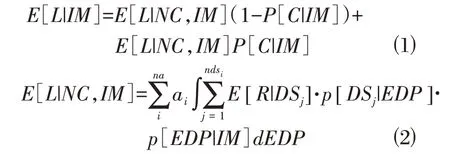
式中：E［L|NC，IM］、E［L|C，IM］分别代表地震强度大小为IM 时，结构未发生倒塌及倒塌时的总损失均值，当发生倒塌时，将整个结构重建所需费用作为结构总损失均值；P［C|IM］为倒塌概率，本文采用动力失稳准则判断结构是否发生倒塌；na 为构件的分组数量；ai为第i 组构件新建所需费用；ndsi为第i 组构件破坏状态等级划分的数量。E［R|DSj］为构件破坏状态等级DSj时的平均损失比，即修复费用与新建费用之比。

通过式⑴、式⑵得到E［L|IM］后，结合地震危险性曲线把地震强度换算为地震动的年平均超越概率，进而获得地震损失的年平均超越概率曲线λ（L）。

1.2 评估流程

根据式⑴、式⑵，得到基于构件变形的地震损失评估流程，如图1所示。

图1 地震损失评估流程Fig.1 Earthquake Loss Assessment Flow Chart

1.2.1 地震危险性分析

地震危险性曲线λ（IM）代表着地震动强度IM 及其对应的年平均超越概率的关系。本文以地震峰值加速度amax为指标来表征地震动强度。文献［2］提出地震危险性曲线的函数表达公式可列为：

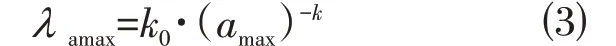
式中：amax为地震峰值加速度；λamax为amax对应的年平均超越概率；k0与k 为待定系数。《中国地震动参数区划图：GB 18306—2015》［12］给出了多遇地震、设防地震、罕遇地震和极罕遇地震的地震峰值加速度及其对应的年平均超越概率，通过数值拟合的方法可以确定待定系数k0与k 的值，进一步确定各设防烈度地区的地震危险性曲线。

1.2.2 地震波选取

地震波的选取合理性将直接对地震损失的评估结果造成影响，因此在选取地震波时务必遵循一定的原则。FEMA P-58认为，在进行损失评估前选取的地震波需要考虑其在结构的主周期段内的形状最接近于目标反应谱，并推荐在进行分析时采用7条地震波。

本文将《建筑抗震设计规范：GB 50011—2010》［13］中规定的反应谱作为目标反应谱。在损失评估前选取20条地震波，所选取的地震波不仅要在结构周期范围内与目标谱形状一致，还必须满足文献［13］对基底剪力的要求。

1.2.3 增量动力分析

要获得完整的地震损失曲线，需考虑地震峰值加速度取值的合理区间。

“小震不坏”作为中国抗震设防的目标之一，结构在小震下基本处于弹性，当地震动强度小于“小震”时，建筑几乎不存在地震损失，因此可以把“小震”对应的PGA 值作为动力增量分析的下限IMmin。对于上限IMmax的取值，假若IMmax过大，所对应的年平均超越概率将很小，既不具备现实意义，计算耗时也会明显增加，故本文取“极罕遇地震”对应的PGA值作为上限IMmax，对应的年平均超越概率为10-4。将区间［IMmin，IMmax］等分为n个子区间，确定出各子区间端点的PGA值，按照从小到大的顺序依次作为动力增量分析的各PGA 值，对选取的地震波进行调幅，进而利用PER⁃FORM-3D软件进行求解。

1.2.4 结构倒塌易损性分析

倒塌准则的选取是否合理对倒塌易损性的分析结果起到关键性影响。本文采用《建筑结构抗倒塌设计规范：CECS 392∶2014》［14］中规定的倒塌判定准则，对结构的倒塌可能性进行判定，当下列任意情况出现时可认为结构将发生倒塌：①弹塑性层间位移角大于1/100；②关键构件的破坏状态达到严重破坏，由于剪力墙是结构的关键抗侧力构件，本文将剪力墙构件作为关键构件。

1.2.5 构件破坏状态判断

对于结构构件和非结构构件分别进行判断，结构构件的损伤识别参数为构件变形，非结构构件的损伤识别参数为层间位移角。

将结构构件的破坏状态划分为完好、轻微损坏、轻中等破坏、中等破坏、比较严重破坏以及严重破坏这6 个性能等级，用DS1～DS6 表示。采用戚永乐［15］的研究中给出的RC 梁、柱、剪力墙构件变形指标限值逐一判断构件的破坏形态，不同破坏状态及其对应的变形限值如图2所示。

根据FEMA P-58 方法的划分准则［7］，将非结构构件的破坏状态划分为OP（立即居住）、LS（生命安全）、CP（尚未倒塌）3 种类型，用DS1～DS3 表示。本文对Vaslani 等人［16-17］的研究结果进行总结，确定了填充墙、门、窗、电梯、水电设施等非结构构件在不同破坏状态下对应的层间位移角限值，如表1所示。

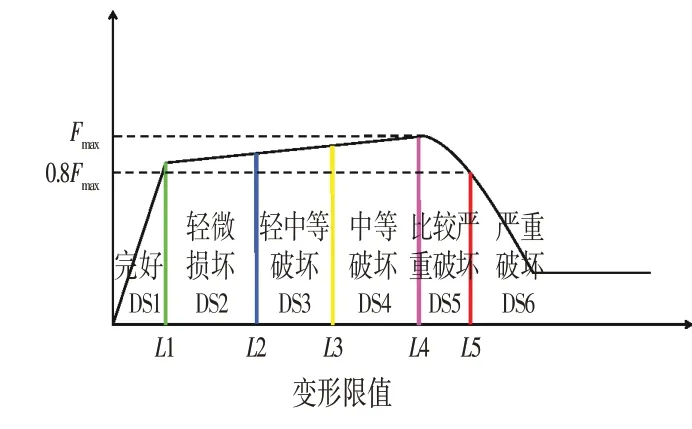
图2 性能水准与变形限值关系示意Fig.2 Relationship between Performance Level and Deformation Limits

表1 非结构构件不同破坏状态对应层间位移角限值Tab.1 Drift Limits of Different Performance Levels for Non-structural Components

1.2.6 构件损失初始化

构件损失初始化的目的在于得到每个构件处于不同破坏状态时的损失期望。构件各破坏状态损失均值的计算如式⑷所示：

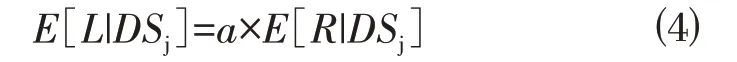
式中：DSj代表构件破坏状态；a 为新建构件的所需费用；E［R|DSj］为当构件的破坏状态为DSj时的损失比均值。对于损失比均值E［R|DSj］的取值，本文基于文献［16-17］建议的构件损失函数进行总结，确定了不同破坏状态下构件的损失比均值，如表2所示。

表2 不同破坏状态下构件损失比均值Tab.2 Component Loss Ratio Corresponding to Different Performance Level

通过综合单价法计算得到新建构件的所需费用a，其中综合单价考虑了材料费、人工费、机械费、管理费、利润等因素。新建构件所需费用的计算如式⑸、式⑹所示。

结构构件：

非结构构件：

由式⑸、式⑹结合表2 可以求取全部构件在不同破坏状态下的损失期望。一旦确定某个（组）构件的破坏状态，即可进一步获取该构件（组）的损失均值。

1.2.7 地震损失计算统计

对结构在每条地震动下的响应进行地震损失计算，计算流程如图3所示。

图3 地震损失计算流程Fig.3 Earthquake Loss Calculation Flow Chart

当所有地震波的每个地震动强度下损失确定后，即可得到不同强度地震的损失期望E［L|IM］，结合地震危险性曲线进而可以得到损失的年平均超越概率曲线λ（L）。

1.3 后处理程序开发

本文根据地震损失的评估流程，基于MATLAB 平台开发了PERFOMR-3D 的后处理程序Loss-Calcula⁃tion，程序主界面如图4所示。

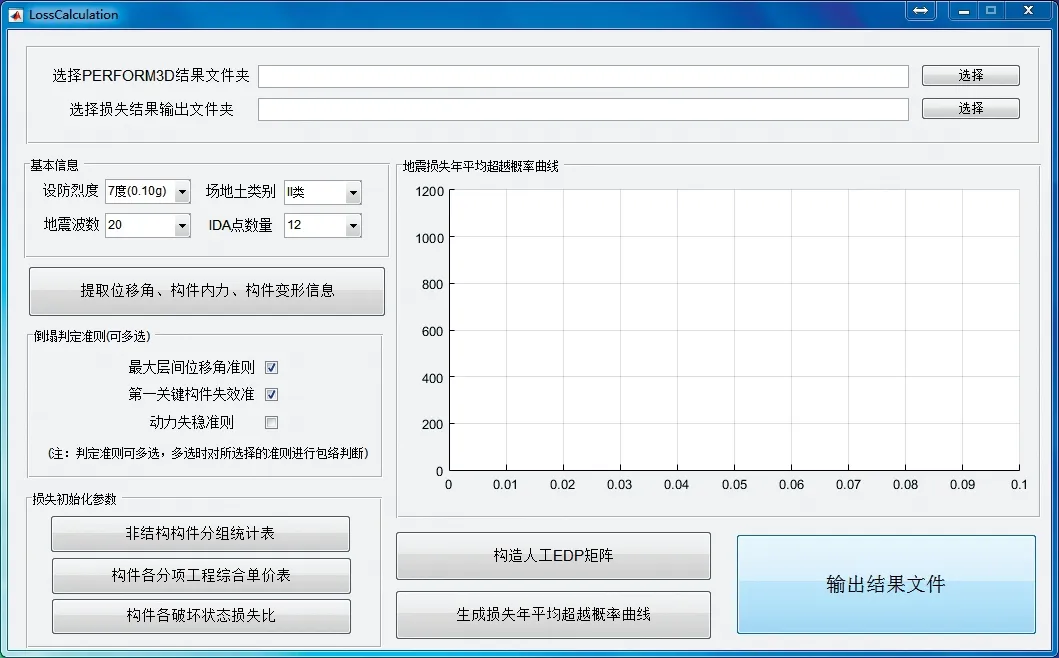
图4 后处理程序的主界面Fig.4 Interface of the Post Program

2 不同设防烈度的框架-剪力墙结构地震损失评估

按照文献［13］进行了6.0度、7.0度、7.5度、8.0度、8.5 度这5 个设防烈度下的框架-剪力墙结构的设计，利用上节所述评估方法分别对其进行损失评估，对比不同设防烈度下结构所承担损失风险的差异。

2.1 模型概况

设计模型为结构总高度达60 m 的17 层结构，除首层层高4.0 m 外，其余层层高3.5 m；场地土为Ⅱ类场地土；标准层结构平面布置如图5所示；小震作用下结构的层间位移角对比如图6所示。

2.2 地震危险性分析

根据《中国地震动参数区划图：GB 18306—2015》［12］，多遇地震、设防地震、罕遇地震和极罕遇地震对应的年平均超越概率分别为0.020 0、0.002 1、0.004 0 和0.000 1。按照1.2.1节方法得到Ⅱ类场地土下各设防烈度的地震危险性曲线，如图7所示。

图5 框架-剪力墙结构平面布置Fig.5 Frame-Shear Wall Structure Layout Plan （mm）

图6 小震层间位移角对比Fig.6 Comparison of Drift Ratio Between Layers under Frequent Earthquake

图7 各设防烈度下的地震危险性曲线Fig.7 Seismic Hazard Curve of Different Seismic Fortified Areas

2.3 地震动选取

地震波按照第1.1.2 节执行，选取得到的20 条地震波信息如表3所示。

2.4 构件破坏状态对比

统计罕遇地震强度的20 条地震波下构件所处的破坏状态，将各设防烈度结构中梁、柱、剪力墙构件的不同破坏状态的发生频率进行对比，如图8 所示。结果表明剪力墙的破坏大多出现在底部的2 个楼层，所以只对底部2个楼层的剪力墙构件进行统计。

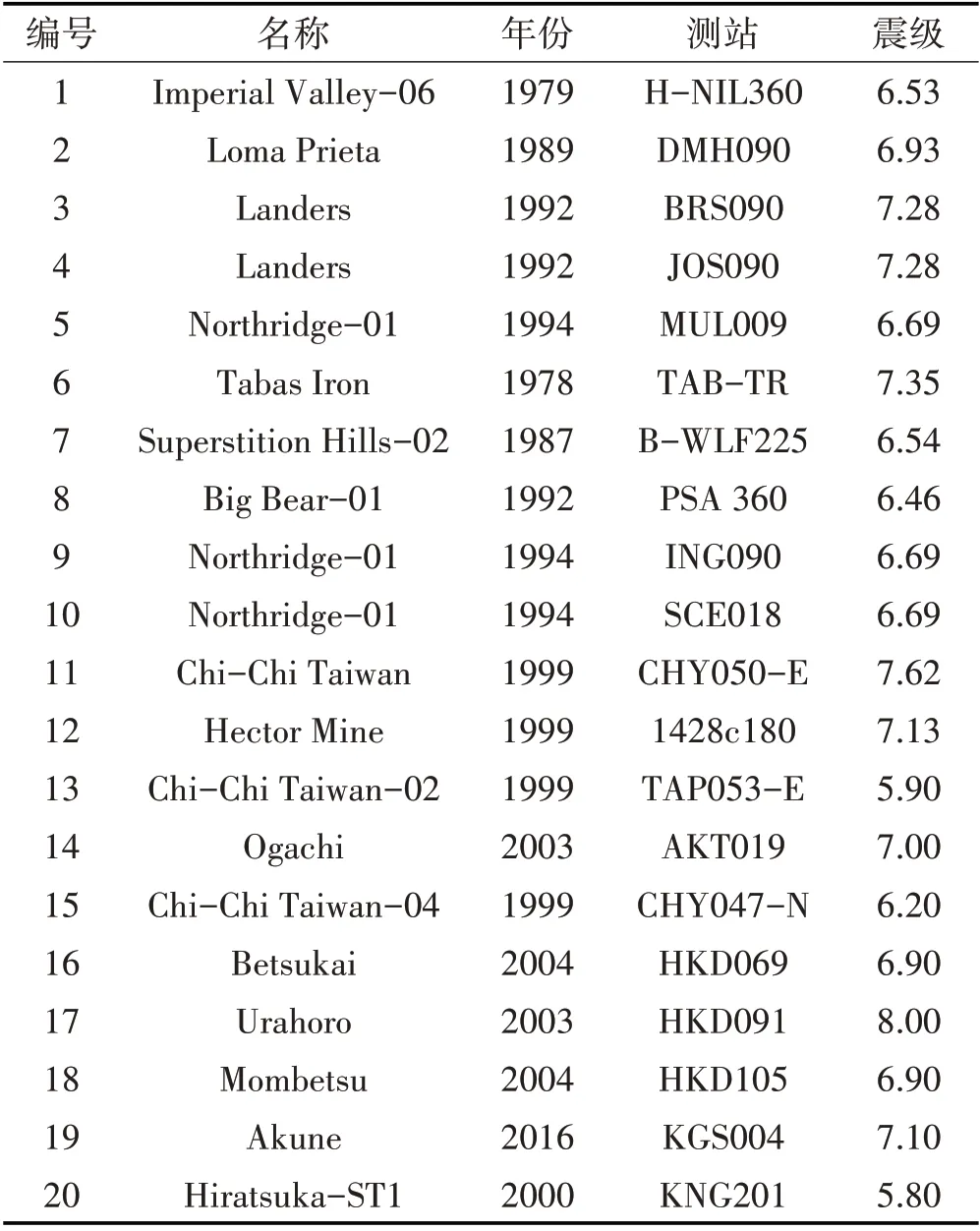
表3 选取的20条地震波信息Tab.3 Selected 20 Ground Motion Records

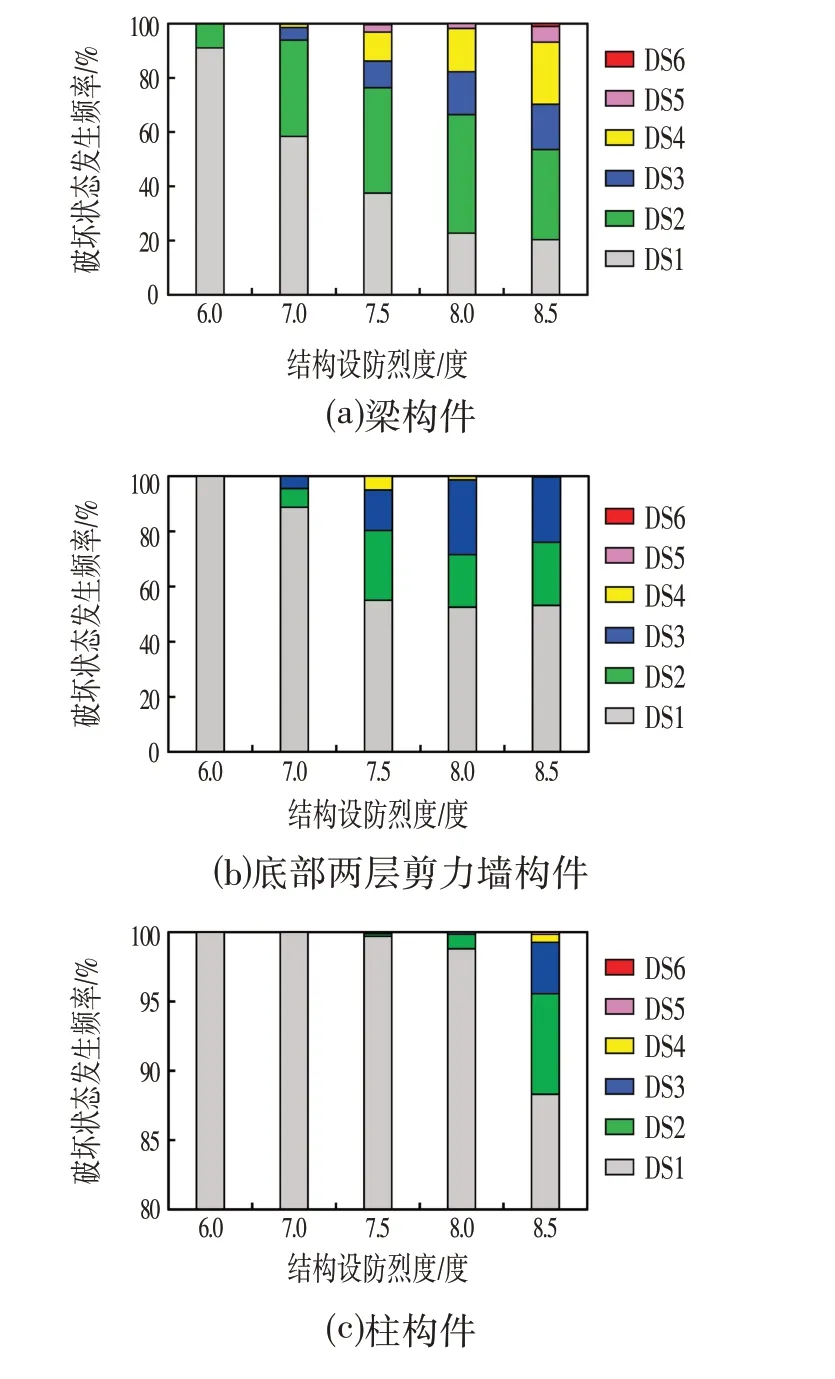
图8 各设防烈度下结构构件破坏状态发生频率Fig.8 Frequency of Component Failure under Different Seismic-Fortification Intensity

由图8可知，随着设防烈度的提高，梁构件呈现越严重的破坏程度；剪力墙构件在6.0度、7.0度、7.5度呈现越严重的破坏程度，并在7.0 度、8.0 度和8.5 度达到接近破坏程度；柱构件在6.0度、7.0度、7.5度基本处于无损坏状态，在8.0度、8.5度破坏程度增加。

2.5 倒塌易损性对比

按照1.2.4节的方法，对结构模型在各条地震波下的倒塌情况进行判断，得到结构在各类设防烈度下的倒塌易损性曲线对比，如图9所示。

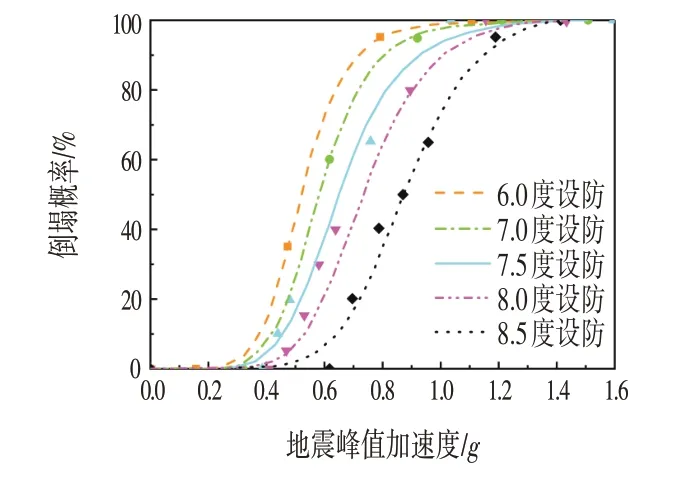
图9 各设防烈度结构的倒塌易损性曲线Fig.9 The Collapse Vulnerability of Each Fortification Structure

倒塌易损性分析的结果如表4所示。结构的抗倒塌安全储备系数CMR 值在1.25～4.43 之间，并且随着设防烈度的提高而下降，7.0 度相对于6.0 度下降幅度最大，说明高设防烈度地区的结构相比于低设防烈度地区将承受更大的倒塌风险，与文献［10］中框架结构的规律一致。

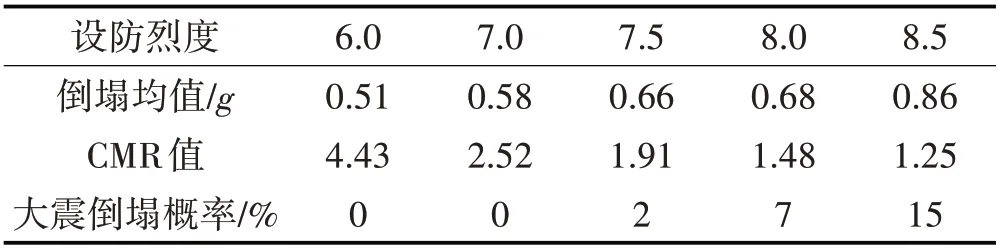
表4 结构倒塌易损性分析结果Tab.4 The Results of Structural Collapse Fragility

2.6 地震损失对比

按照1.2.6 节方法计算构件各破坏状态的修复费用，结构构件和非结构构件的新建费用计算见表5、表6。利用后处理程序计算得到大震与极罕遇地震下的期望损失比，如表7所示。

结构构件和非结构构件的损失比都随着设防烈度的提高而增加。其中，7.5 度、8.0 度和8.5 度设防结构损失比较接近；6度设防结构的构件损失比小于2%。

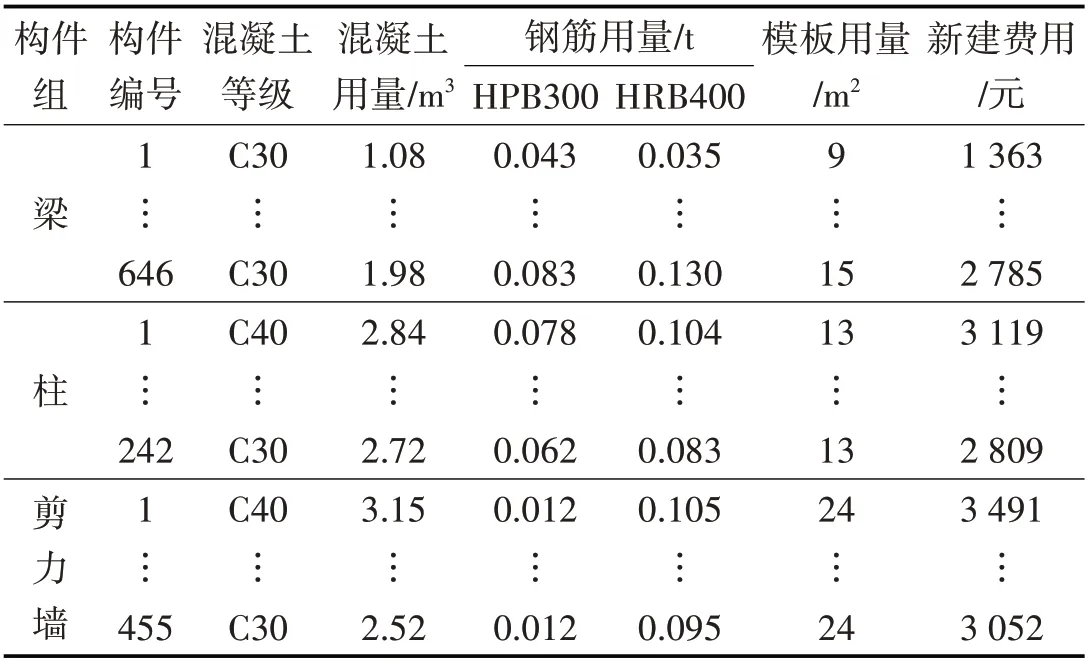
表5 结构构件新建费用统计Tab.5 The Cost Statistics for New Structural Components

表6 非结构构件新建费用统计Tab.6 Cost Statistics for New Non-structural Components

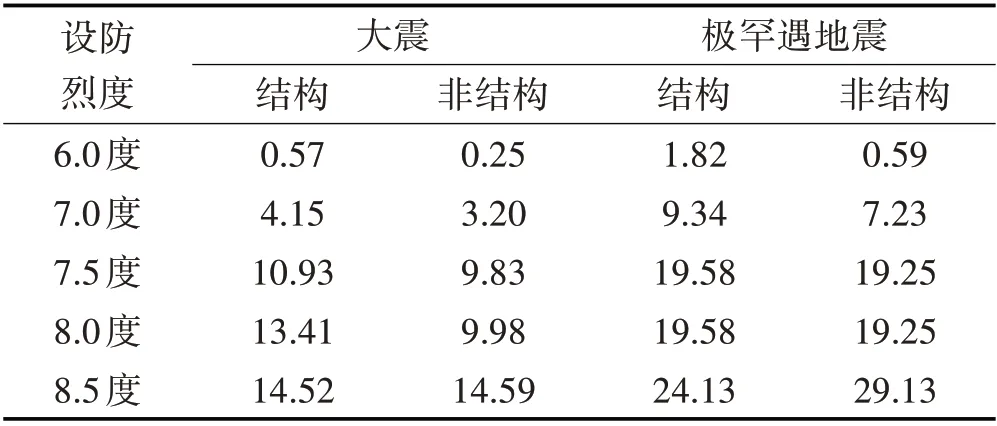
表7 损失比均值对比Tab.7 Comparison of the Average of Loss Ratio （%）

就结构构件而言，8.0 度和8.5 度的损失比相当，把7.0 度设防下的损失作为参照，7.5 度下的构件损失为7.0 度的2.0～2.6 倍，8.0 度和8.5 度下的构件损失为7.0度的2.6～3.5倍。

就非结构构件而言，7.5度和8.0度的损失相当，把7.0度设防下的损失作为参照，7.5度和8.0度下的构件损失为7.0度的2.7～3.2倍，8.5度下的构件损失约为7.0度的4倍。

绘制不同设防烈度下结构总损失比的年平均超越概率曲线，如图10 所示。由图10 可知，6.0 度设防结构的损失比最小；7.0 度设防结构损失比相比6.0 度更大；7.5 度、8.0 度与8.5 度3 种设防烈度下结构的损失大小相当，处于同一水平，在极罕遇地震下三者的损失比均在30%左右。

图10 年平均超越概率曲线对比Fig.10 The Comparison of Annual Average Exceedance Probability

将5个结构在多遇地震下的最大层间位移角进行对比。对比结果表明，6.0度结构的层间位移角最小，7.0度结构略大，7.5度、8.0度和8.5度结构的最大层间位移角大小相当，结构的最大层间位移角与损失比在一定程度上呈现着正相关关系，在多遇地震下结构最大层间位移角越小，所承受的损失风险也越小。

对图10中的年平均超越概率曲线进行积分，可以得到各结构的年平均期望损失EAL，如表8所示。

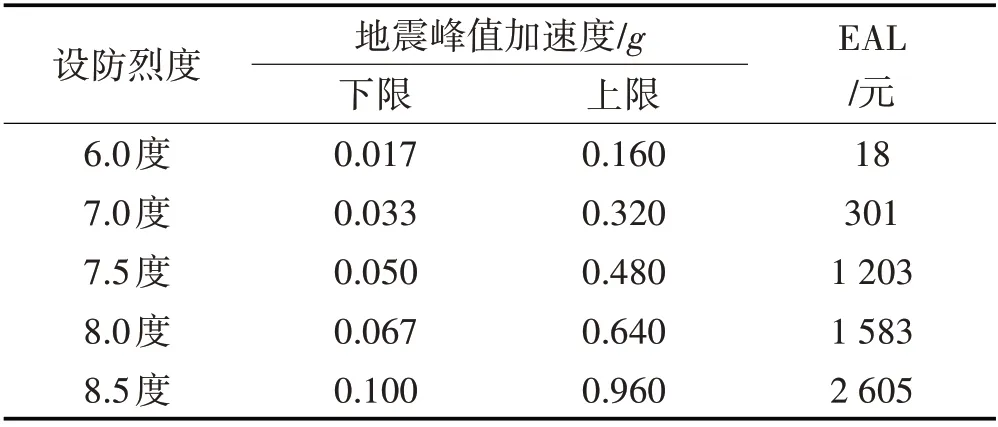
表8 年平均损失期望Tab.8 Expected Annual Loss

2.7 地震损失影响因素分析

2.7.1 地震强度的影响

年平均损失期望EAL，是用来表征不同强度地震共同作用的指标。文献［10］提出利用式⑺能将不同强度地震对EAL值的贡献进行分解，地震强度影响系数值的大小表征了该地震强度对损失的影响程度。

式中：λ'（IM）为地震危险性曲线在IM 处的导数，EAL为年平均损失期望。通过该方法能够对不同强度地震动的影响系数进行求解，如图11所示，鉴于6.0度设防结构几乎不存在损失，地震动影响系数无实际意义，因此不对6.0度结构进行分析。

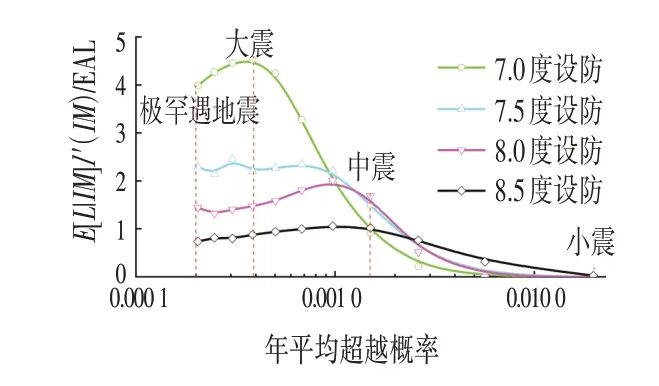
图11 地震强度影响系数分布Fig.11 The Distribution of Seismic Intensity Influence Coefficient

由图11 可知，7.0 度设防结构的损失主要由大震和极罕遇地震引起，中、小震下损失占比很小。当设防烈度提高，大震下的损失占比呈现降低趋势，与此同时中、小震下的损失占比提高；就8.0 度结构而言，设防烈度下的地震损失占比相对最高；就8.5 度结构而言，其地震强度影响系数曲线较为平缓，地震损失对不同地震强度的敏感性较小。

2.7.2 不同构件类型的影响

首先对结构构件和非结构构件在不同地震强度下的损失占比进行分析，不同地震强度下结构构件在总损失中的占比如图12 所示。由图12 可知，6.0 度设防结构的损失以结构构件为主，结构构件损失占比随地震强度增大呈现下降趋势；7 度设防结构的损失在小强度地震下以结构构件为主，且结构构件损失占比随地震强度提高呈现下降趋势，但相比6.0 度设防结构其下降幅度更加明显，在中、高强度地震下起主导作用的构件由结构构件转为非结构构件；7.5度、8.0度及8.5 度设防结构的结构构件损失占比受地震强度变化的影响不大，其损失占比基本在20%～40%内。

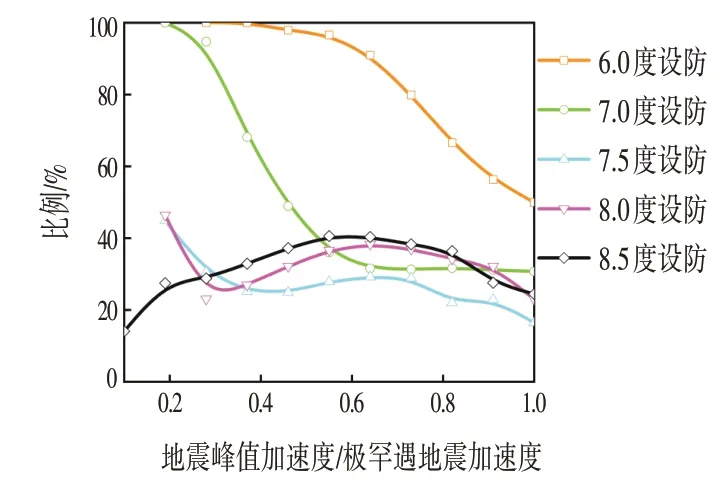
图12 结构构件损失占比Fig.12 The Loss Ratio of Structural Components

对于结构构件和非结构构件，不同地震强度下不同构件的损失占比情况如图13所示。在结构构件中，梁破坏程度最为显著，其损失占比基本超过结构构件总损失的80%；底层剪力墙构件随设防烈度提高开始呈现不同程度的破坏，其占比有所提高，剪力墙构件在8.0 度和8.5 度下的损失占比相当，基本约为15%～20%；柱构件仅在8.5 度结构中出现了局部的轻微破坏，占比非常小。在非结构构件中，不同类型构件的损失占比与设防烈度的相关性较小，水电设施的损失占比达到50%左右；其次是填充墙，损失占比约为20%～30%；门窗类的损失占比不到5%。