计及电动汽车的电力系统事件触发负荷频率控制

曾小波，旷永红，宋俊辉

（1.湖南理工职业技术学院智能制造学院，湘潭 411104；2.湖南工程学院电气与信息工程学院，湘潭 411104；3.上海中车艾森迪海洋装备有限公司，上海 201306）

近年来，电动汽车既可作为用电设备，又可作为移动的、分布式的电源接入电网，由于其所具有的一些友好的环境特征，如减少温室气体排放和噪声污染，已有文献对电动汽车接入智能电网方面进行研究[1-4]。作为储能装置，由于电动汽车电池的快速响应[5]，电动汽车群在稳定负荷需求和风力发电的波动方面非常有效[6]。电动汽车的功率输出可以通过分散的本地插头[7]、负荷估计器[8]处测量的负荷偏差以及聚合系统采集或通过的分布式信号进行调节。另一方面，电动汽车群可以参与负荷频率控制，迅速稳定系统扰动所造成的频率波动[9]。利用双向电力电子设备[10]和电动汽车入网V2G（vehicle-to-grid）技术，将电动汽车作为电力系统中的储能装置，可以协助电力单元实现快速响应以达到负荷频率控制的要求。

本文假设存在大量可用的电动汽车，因此存在足够的电能储备用以协助传统电力单元进行频率调节。电动汽车通过聚合器进行聚合和管理，电动汽车聚合器的概念已得到广泛应用[9,11-13]，聚合器将收集到的电动汽车信息和状态发送到控制中心，并将控制中心的控制指令重新分配给各电动汽车。在实施方面，将电动汽车接入智能电网需要开放的通信基础设施，例如网络控制或广域通信系统，用以实时更新包括电池充电状态、功率容量以及连接数量等电动汽车数据信息。因此，通信信道拥塞、数据包丢失等通信故障，以及相关的时间延时都是不可避免的，这些的发生会降低系统的动态性能，甚至影响闭环系统的稳定性。

现有文献多为对电动汽车参与电力系统调频的研究，对上述问题鲜有研究。因此，针对上述问题，本文将事件触发控制机制引入计及电动汽车的电力系统负荷频率当中。最近几年，由于能够在保证期望的系统性能的同时减少传输的信息量，事件触发控制的思想引起了广泛关注[14-16]。在事件触发控制系统中，信号基于事件触发机制进行传输，即只有当给定的触发条件满足时，信息才进行传输，因此能够在一定程度上减少网络负担和能源消耗。目前，事件触发思想已被应用于电力系统控制当中，文献[17]首次将事件触发思想引入电力系统中，减少了传输的数据量，但是推导出的稳定性判据中存在大量的自由权矩阵，运算量过大。

本文在考虑电动汽车群接入带来延时的情况下，引入事件触发控制机制，将闭环系统建立为时滞系统模型，对系统进行稳定性分析，并联合求出控制器增益和事件触发矩阵，从而在减小通信负担的同时达到良好的控制效果。

1 系统模型

1.1 包含EVs 的电力系统负载频率控制模型

电动汽车群利用开放的网络，通过聚合器实时获取控制指令、传输自身数据信息，这就导致控制中心、聚合器和电动汽车之间的传输回路中会出现诱导时延。以两域电力系统为例，包含电动汽车群的电力系统负荷频率控制框图如图1 所示。

控制命令按比例αgi和αei进行分配，其中发送给聚合器的命令为αeiui（t-hi（t）），h（t）是控制中心和聚合器之间的时延。为了便于描述，本文采用具有时间常数Te和电池系数Ke的一阶EVs 动力学模型，该模型在文献[9、18-19]中也得到广泛应用，因此EVs 的输出功率可以表示为

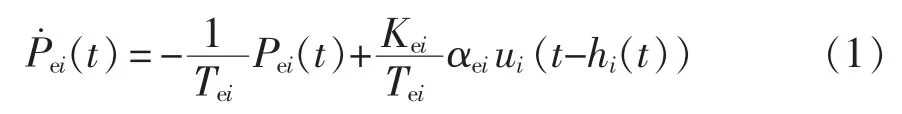
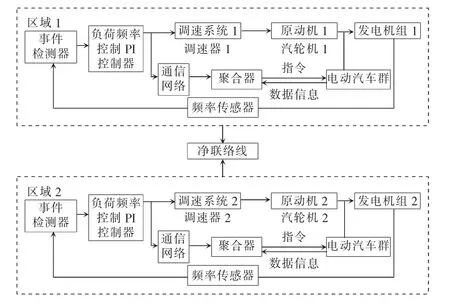
图1 包含电动汽车的两域电力系统负荷频率控制框图Fig.1 Control block diagram of load frequency of twodomain power system including electric vehicles

图2 描述了包含电动汽车群的多域电力系统模型[12-13]，图中Mi为发动机转动惯量，Tgi为调速器时间常数，Di为负荷阻尼常数，Tchi为涡轮机时间常数，ri为转速，βi为频率偏差系数，Tei为电池时间常数，Kei为电池系数，Δfi为频率偏差，ΔPd为负荷扰动量，ΔPmi为发电机机械功率输出偏差，ΔPvi为调速器控制阀位置偏差。

从而，在考虑网络诱导时延的情况下，可以得到包含EVs 的多域电力系统负荷频率控制状态空间模型为

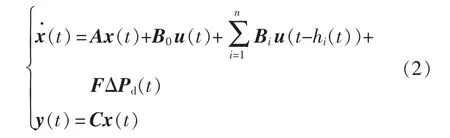
式中：x（t）为状态变量；y（t）为输出变量；ΔPd（t）为负荷扰动。具体的数学表达式分别为

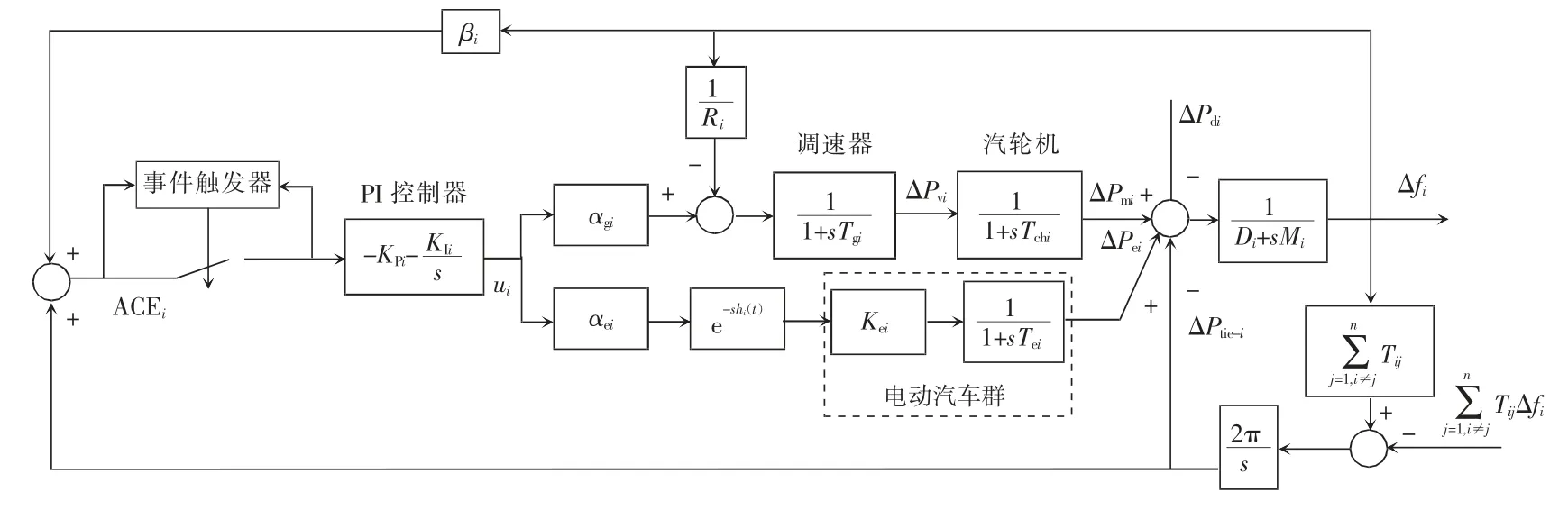
图2 基于事件触发机制的多域电力系统模型（i=1，2，…，n）Fig.2 Multi-domain power system model based on event-triggered mechanism（i=1，2，…，n）

将区域控制偏差ACE（area control error）作为控制器输入，设计PI 型负荷频率控制器，即

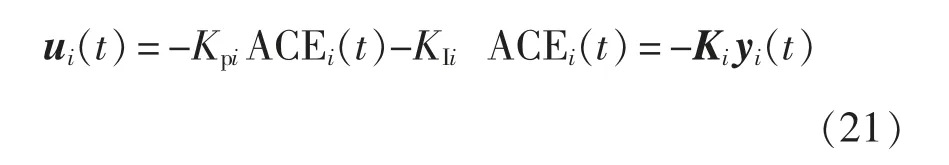
式中，Ki=[KPiKIi]，KPi和KIi分别表示比例增益和积分增益。

1.2 事件触发通信机制

本文采用的事件触发机制为

式中：ey=y（tkh+jh）-y（tkh），j∈N；tkh 表示触发时刻，其中，t0h=0。当违背上述条件时，测量数据被释放到通信网络，由于实际电力网络中存在网络延时，时刻数据被传输到控制器侧，为网络传输时延，其最大值为dM。Ω＞0 为触发加权矩阵，σ∈[0，1）是事件触发参数，当σ=0 时，事件触发机制退化为周期触发。

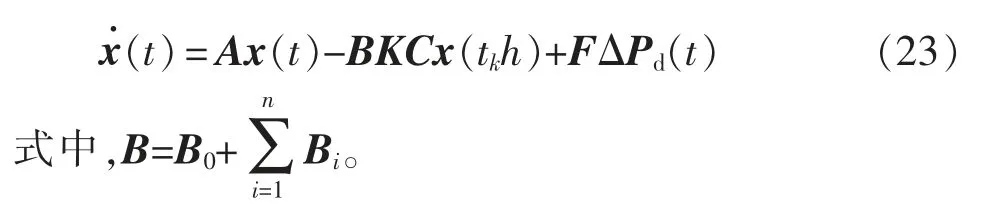
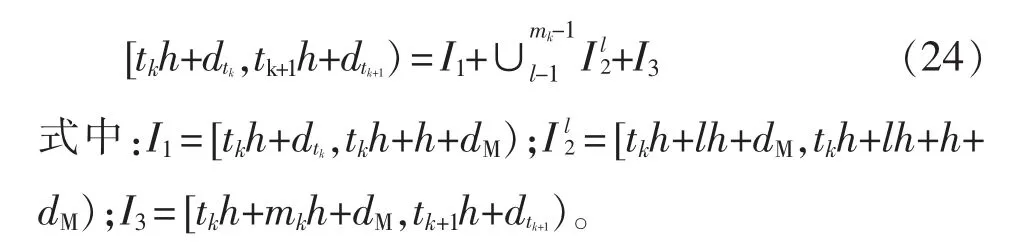
定义函数e（t）和时滞函数τ（t），分别为

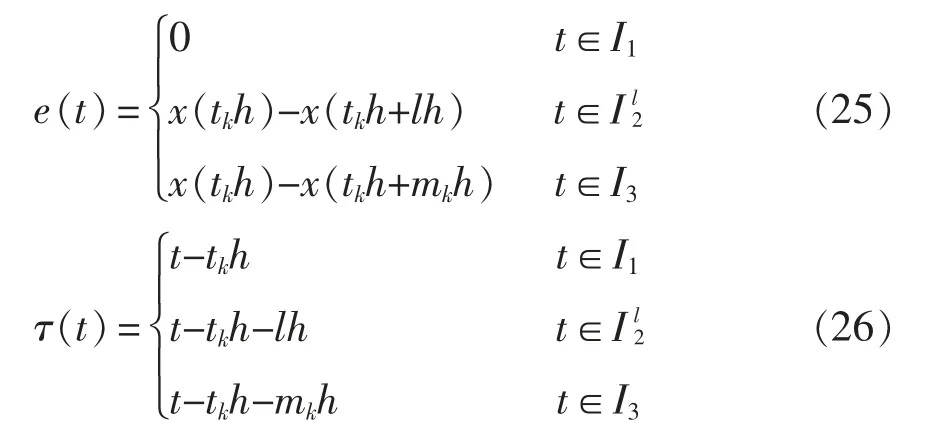
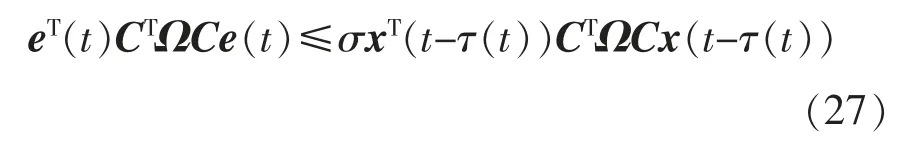
因此，t∈[tkh＋dtk，tk＋1h＋dtk＋1）时，系统可以变形为

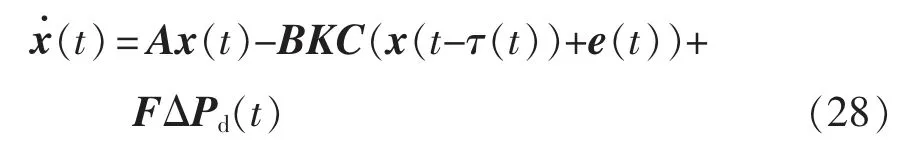
本文的主要目的是在节约通信资源的情况下，研究电力系统的稳定性，设计静态输出反馈控制器和事件触发机制，同时保证：当负荷扰动ΔPd（t）=0时，系统式（28）渐近稳定；当任意非零扰动ΔPd（t）∈L2[0，＋∞），不等式||y（t）||2≤γ||ω（t）｜｜2成立，其中γ表示H∞性能指标，是给定的正实数。

2 事件触发机制与H∞控制器联合设计

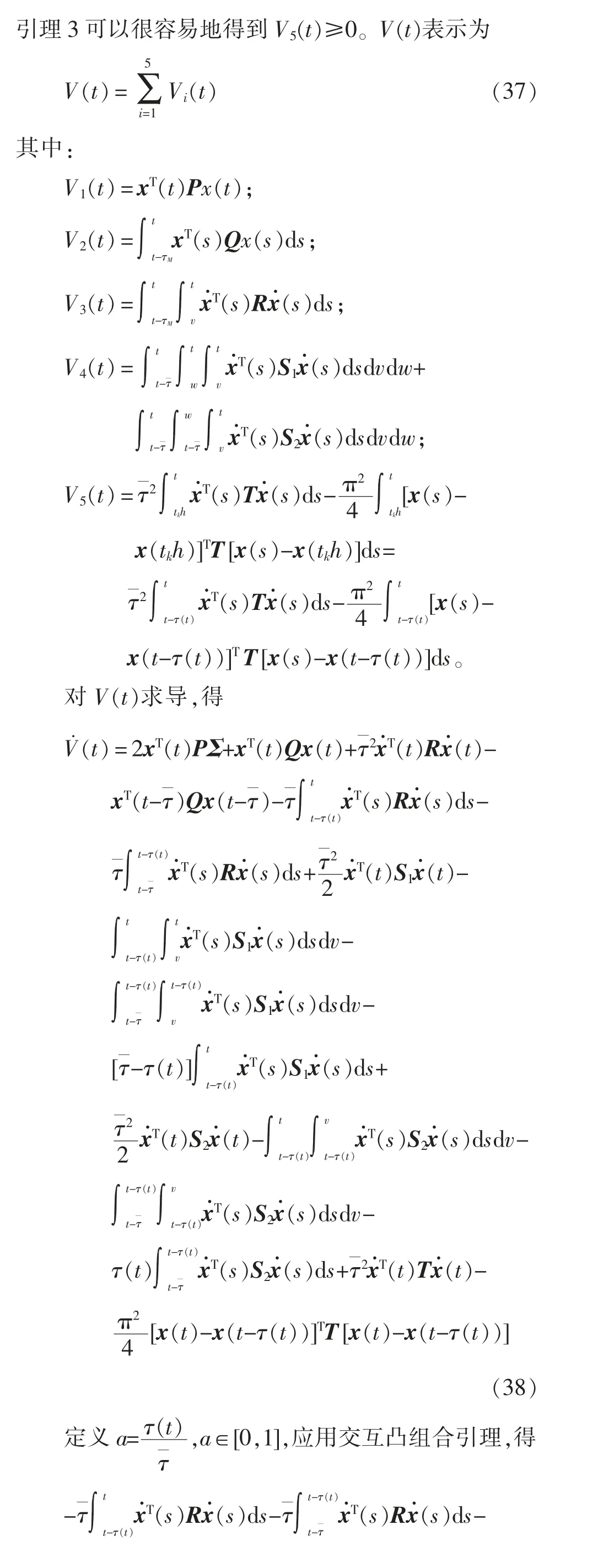
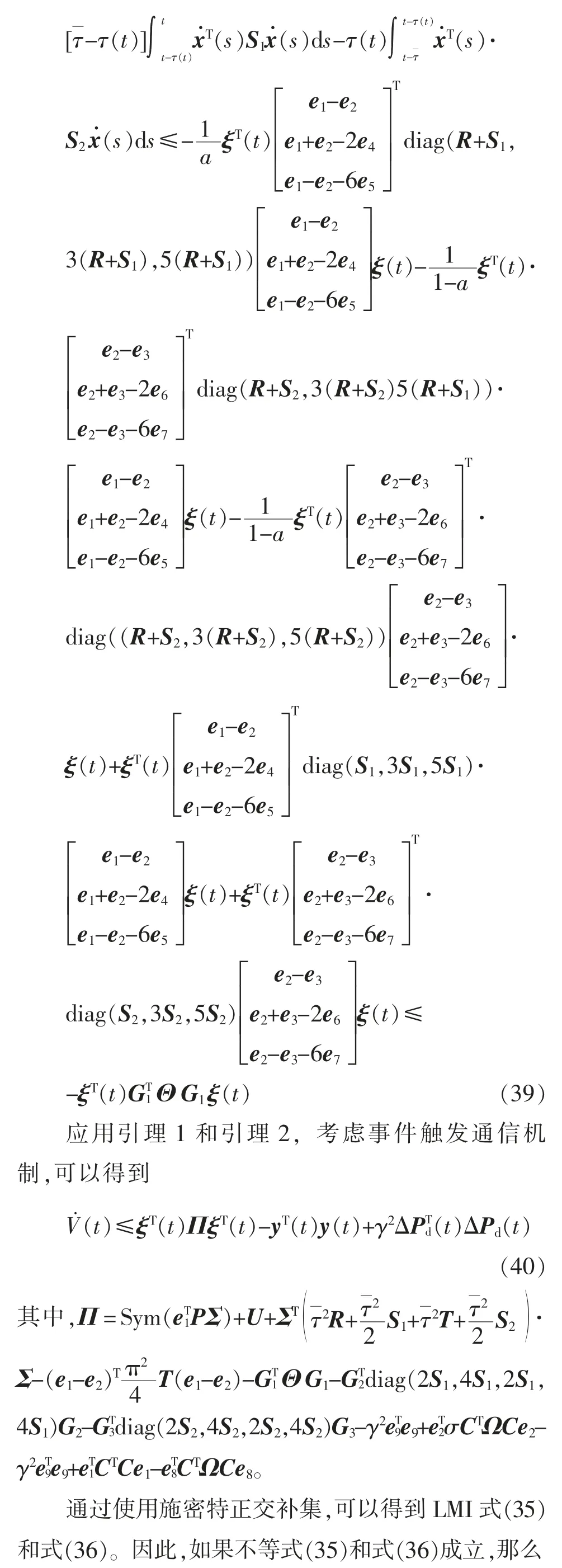
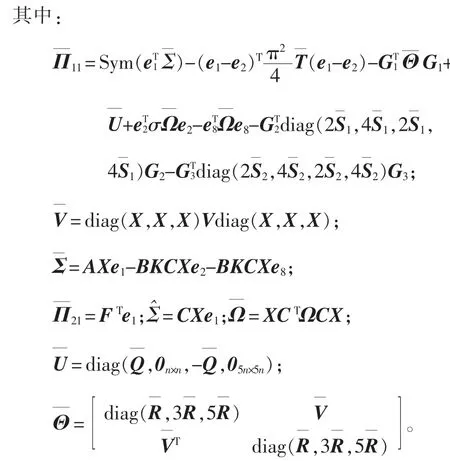
证明：定义X=P-1，用diag{X，X，X，X，X，X}左乘右乘不等式（35），用左乘右乘不等式（36），并且对矩阵变量进行如下变化：，使用引理4 和施密特正交补集，从而可以得到不等式（44）和式（45）。

3 仿真案例

本节旨在验证第2 节所提定理的有效性，对PI控制器和触发参数进行协同设计，从而有效实现频率控制，减少通信负担。LFC 系统如图1 所示，其中相关参数见表1。

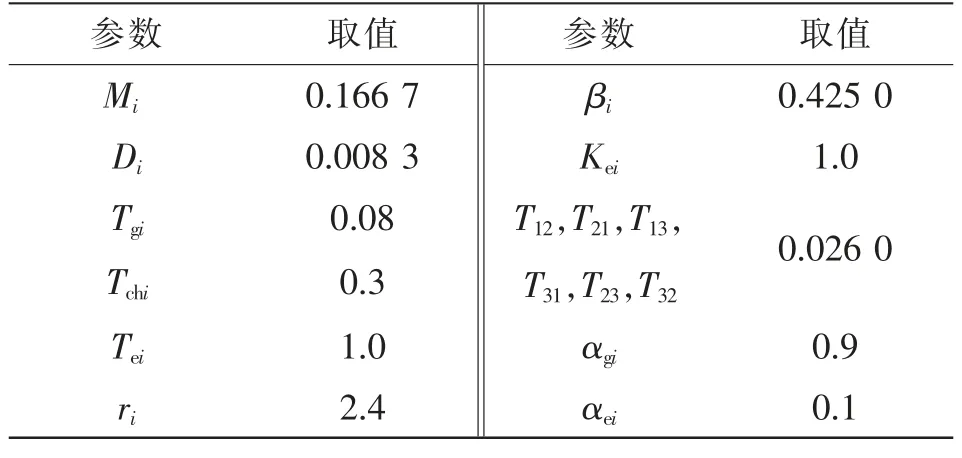
表1 三域LFC 模型参数（i=1，2，3）Tab.1 Parameters of three-domain LFC model（i=1，2，3）

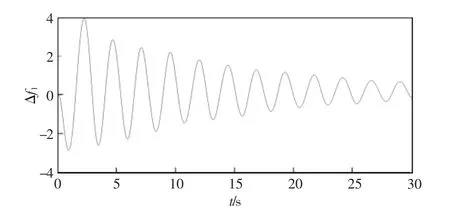
图3 系统频率变化曲线（区域1）Fig.3 Frequency variation curve of system（domain 1）

以区域1 为例，触发参数σ 与释放次数（即触发次数）之间的关系如表2 所示。σ=0 时，事件触发退化为时间触发，由表中可以看出，与时间触发相比，事件触发能够有效减少传感器释放次数，节约通信资源。此外，表中还列出了数据发送率，随着触发参数σ 的增大，释放次数减少，采样信号发送率降低（数据发送率=（N/N0）×100%，其中N 表示σ≠0时采样信息的释放次数，N0表示σ=0 时采样信息的释放次数），因此可以通过增大触发参数降低网络通信负担。

表2 σ 不同时对应的释放次数Tab.2 Release times for different values of σ

4 结语

本文针对网络环境下包含电动汽车的LFC 系统稳定性问题，提出了一种基于事件触发机制的控制方法，减少了系统通信负担。利用李雅普诺夫稳定性理论，对系统进行稳定性分析，并联合求出控制器增益和事件触发矩阵。需要注意的是，在时滞依赖稳定性条件的推导中，基于B-L 积分不等式对单重积分和二重积分进行约束，从而得到保守性较小的稳定性条件。最后，通过系统仿真，验证了所提方法的优越性。