基于改进MMAS 算法的双有源桥变换器PI 参数优化
2021-06-05林安娜谢运祥
林安娜,谢运祥
(华南理工大学电力学院,广州 510640)
双有源桥DAB(dual active bridge)变换器自提出以来,因其具有电气隔离、能量双向传输、高功率密度、模块化、轻量化、利于实现软开关等优点[1-2],广泛应用于电动汽车、分布式发电、固态变压器等领域[3-6]。然而,目前对DAB 变换器的基本控制单元PI控制器的参数优化研究较少。PI 控制器的参数将直接影响DAB 变换器的动态响应,因此研究PI 控制器参数优化具有重要意义。
近年来,随着智能算法的发展,采用蚁群算法ACA(ant colony algorithm)对PI 控制器进行参数优化成为了一种有效手段[7-9]。ACA 作为一种仿生优化算法,采用分布式并行计算机制,易与其他方法结合,并且能更好适应被控对象的非线性特性,具有较强的鲁棒性[10]。文献[11]针对风力发电系统中最大风能追踪问题,提出了一种基于ACA 的自整定PID 控制方法,但该方法易发生早熟收敛现象,并使PID 控制器参数陷入局部最优解。文献[12]为了缓解风机的不平衡载荷和改善风机的振动状态,针对风机变桨系统提出了一种自适应调整信息素挥发系数的ACA 控制策略。文献[13]针对高压直流输电系统PI 控制器的参数优化问题,提出了一种自适应调整信息素挥发系数的改进蚁群优化算法。自适应调整信息素挥发系数的ACA 能在保持较高收敛速度的情况下提高全局搜索能力,但在信息素更新方面,难以强化最优信息反馈,收敛速度还有待提高。文献[14]以DAB 变换器为被控对象,基于ACA 设计了二阶控制器和PI 控制器,但PI 控制器对应系统的鲁棒性较差。文献[15]针对传统ACA 存在的全局搜索能力低,早熟停滞等问题,提出一种基于最大最小蚂蚁系统MMAS(max-min ant system)进行PID 参数整定的新型算法MPID,但其节点能见度有待改进。以上文献所提算法仍存在提高全局搜索能力和保证收敛速度之间的矛盾、强化最优信息反馈和寻找全局最优解之间的矛盾。在一定的时间空间复杂度下,算法的寻优能力有待进一步提高。
为了解决以上问题,本文提出一种基于改进MMAS 算法的DAB 变换器PI 参数优化方法。该方法通过优化节点能见度和信息素更新机制,在提高全局搜索能力的同时保证了较快的收敛速度,有利于求得全局最优解,有效避免了节点信息素浓度差异过大导致算法发生早熟收敛现象,提高了算法在一定时间复杂度和空间复杂度下的寻优能力。首先对DAB 变换器建立小信号模型,然后提出一种改进MMAS 算法,介绍了基于改进MMAS 算法的DAB 变换器PI 参数优化结构和流程。最后,以DAB 变换器的时间与误差绝对值乘积积分ITAE(integral of time-weighted absolute error)性能指标为目标函数,采用改进MMAS 算法对PI 控制器参数进行优化,通过仿真和实验验证了该算法的有效性。
1 DAB 变换器小信号建模
图1 为DAB 变换器的拓扑,它主要由全桥变换器、直流电容、辅助电感和高频变压器组成。高频变压器给电路提供电气隔离和电压匹配,辅助电感为瞬时能源存储设备。全桥H1桥和H2桥的直流端电压分别为vi和vo;全桥H1桥的交流端电压为vH1;全桥H2桥的交流端电压为v'H2,折算到变压器原边侧后的电压为vH2;辅助电感两端的电压为vL。

图1 DAB 变换器的拓扑Fig.1 Topology of DAB converter
DAB 变换器的基本工作原理波形如图2 所示,全桥H1桥和H2桥的斜对角开关管驱动脉冲相同,同一桥臂的开关管180°互补导通,在开关管S1和Q1间存在移相比D。vH1和vH2均为占空比为50%的方波,两者之间存在移相时间DThs,其中Ths为半个开关周期。通过控制vH1和vH2的移相比D 可以控制传输功率的大小和方向,传输功率的表达式为
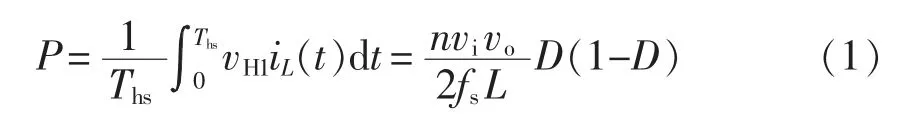
式中,n 为变压器的变比;D 为半个开关周期内的移相比,0≤D≤1;fs为开关频率,fs=1/(2Ths)。

图2 基本工作原理波形Fig.2 Waveforms under the basic operating principle
DAB 变换器的建模有利于简化系统,其研究较为广泛[16-17]。通过状态空间平均法,建立DAB 变换器的小信号模型[18]为



图3 DAB 变换器的小信号模型Fig.3 Small signal model of DAB converter
2 基于改进MMAS 算法的DAB变换器PI 参数优化
改进MMAS 算法的基本参数定义为

式中:m_iter为算法的循环次数;n 为蚂蚁数量;α为信息启发式因子;β 为期望启发式因子;ρ为信息素挥发系数;Q 为信息素释放量;τmax和τmin分别为节点信息素浓度的最大值和最小值。
本节以PI 参数优化问题为背景介绍改进MMAS 算法的基本原理。PI 控制器的传递函数可以描述为
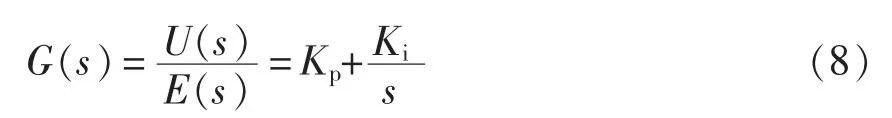
式中:U(s)为控制量;E(s)为误差;Kp为比例增益;Ki为积分增益。
2.1 节点和路径
以PI 控制器的参数Kp和Ki作为待优化变量,根据被控对象的特性,设置Kp和Ki的有效数位和小数点。假设Kp和Ki都有5 个有效数位,其中Kp有2 位整数,3 位小数;Ki有4 位整数,1 位小数。Kp和Ki的值在XOY 平面的抽象表示如图4 所示,其中横坐标K1~K5表示Kp的各数位,K6~K10表示Ki的各数位,纵坐标表示各数位的取值范围(0~9 的整数)。当一只蚂蚁完成一次循环时,该路径有10个节点的信息。这条路径所对应的Kp和Ki值表达式为

由此,图1 蚂蚁所示路径的PI 参数值为:Kp=24.872,Ki=1 365.2。

图4 节点和路径示意Fig.4 Schematic of nodes and paths
2.2 目标函数
为使系统具有良好的性能,要根据系统的性能指标建立目标函数。改进MMAS 算法在建立目标函数时引入了ITAE 性能指标,该性能指标能综合考虑控制系统的响应速度和抑制干扰信号的能力,并兼顾系统的超调量和调节时间,其表达式为

式中:vo_err(t)为DAB 变换器输出电压参考值与实际值的误差;t 为时间。目标函数定义为

式中:γ0为Z-N 法得到的系统ITAE 性能指标;γ 为每只蚂蚁路径所对应的系统ITAE 性能指标。目标函数初始值J0=1。
2.3 节点转移概率
假设每只蚂蚁从线段Kk-1列上任意节点爬行到Kk列上任意节点的时间相等。所有蚂蚁都从K1列出发最终爬到K10列,完成一次循环。则第m 次循环中,某只蚂蚁从节点(Kk-1,i)爬行到(Kk,j)的概率为

式中:α 为信息启发式因子,表示信息素的重要性;β 为期望启发式因子,表示能见度重要性;i、j、s 为0~9 的整数,表示节点纵坐标值;τm-1(Kk,j)为第m-1次循环结束后节点(Kk,j)的信息素浓度;η(Kk,j)为节点(Kk,j)的能见度。节点能见度为某一列上节点相对于上一次循环中该列最优节点的能见度,其定义为

式中jopt(0~9 的整数)按如下方式取值:第一次循环中,jopt为Z-N 法计算的Kp和Ki值所映射节点的纵坐标值;以后的每次循环中,jopt为上一次循环最佳目标函数值对应的Kp和Ki值所映射节点的纵坐标值。
2.4 信息素更新
1)最优路径对应的节点更新信息素
改进MMAS 算法仅让每次循环中目标函数值最小的蚂蚁路径所对应的节点更新信息素,信息素更新公式为

式中:ρ 为信息素挥发系数,取值范围为0~1;Q 为信息素释放量,为常数;Δτm(Kk,j)为第m 次循环后的信息素增量;Jm_a为第m 次循环中第a 只蚂蚁路径所对应的目标函数值;Jmin为第m 次循环中的最小目标函数值,即本次循环最优解。Jmin的取值可以为本次循环最优解或全局最优解。通过大量的仿真表明,两者的求解效果相近,但采用本次循环最优解能使算法收敛速度更快。
2)信息素限制
改进MMAS 算法设置了节点信息素浓度的最大值τmax和最小值τmin。每次循环后,节点信息素浓度会按照信息素挥发系数ρ 减小信息素,只有本次循环最优路径所对应的节点会增加信息素。为避免经过多次循环后某些节点上的信息素浓度远大于其他节点,算法陷入局部最优造成停滞现象。改进MMAS算法限制了每个节点信息素浓度都在区间[τmax,τmin],使得更大范围内的最优解搜索得以进行,即

3)信息素初始化
改进MMAS 算法设置了节点信息素初始浓度为最大值τmax,这样使得第m 次循环后,节点之间信息素浓度的差异最多为(1-ρ)m倍,节点信息素浓度的相对差异缓慢增加,使算法在初期能够搜索到更多可行解,利于提高全局搜索能力。
4)信息素重置
当求得的最优值在N 次循环中没有明显改进时,改进MMAS 算法对节点信息素浓度重置为

改进MMAS 算法仅让每次循环中目标函数值最小的蚂蚁路径所对应的节点更新信息素,强化正反馈机制利于寻得最优解,并防止蚂蚁选择较差路径后节点信息素浓度依然增加。改进MMAS 算法通过取消约束条件和强化最优信息反馈提高了收敛速度,通过信息素限制、初始化和重置提高了算法的全局搜索能力,保证了算法的扩散性。
2.5 PI 参数优化
以DAB 变换器为被控对象,采用改进MMAS算法优化PI 控制器的结构如图5 所示,考虑到DSP 采样及运算等因素,增加了延时环节e-Tds。其中,vo(s)和vo_ref(s)分别为输出电压实际值和参考值。基于改进MMAS 算法PI 参数优化的流程如图6 所示。

图5 改进MMAS 算法优化PI 控制器的结构Fig.5 Optimization of PI controller structure using the improved MMAS algorithm

图6 基于改进MMAS 算法PI 参数优化的流程Fig.6 Flow chart of PI parameters optimization based on the improved MMAS algorithm
3 仿真与实验验证
对基于改进MMAS 算法优化PI 参数的DAB变换器进行仿真和实验验证。DAB 变换器如图2所示,仿真和实验参数见表1。
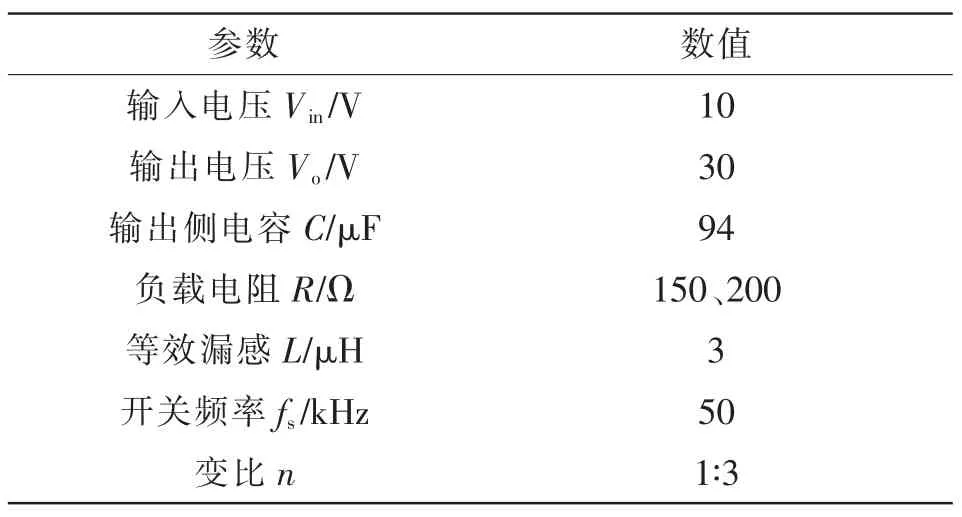
表1 DAB 变换器参数Tab.1 Parameters of DAB converter
3.1 仿真结果及分析
在Matlab/Simulink 平台搭建DAB 变换器模型,其中PI 控制器的Kp、Ki值采用改进MMAS 算法进行优化。改进MMAS 算法基本参数设置:循环次数m_iter=100,蚂蚁数量n=30,信息启发式因子α=0.9,期望启发式因子β=2,信息素挥发系数ρ=0.02,信息素释放量Q=5,节点信息素浓度的最大值τmax=100,最小值τmin=50。利用Z-N 法获得的PI 参数为Kp=0.254,Ki=3 845.5,并以此作为初始值,分别采用ACA 和改进MMAS 算法对PI 参数进行寻优。ACA的PI 参数为Kp=2.941,Ki=1 107.6;改进MMAS 算法的PI 参数为Kp=1.502,Ki=307.1。仿真设置在t=8 ms 时,负载由200 Ω 突变为150 Ω。Z-N 法、ACA和改进MMAS 算法优化PI 参数的DAB 变换器系统响应仿真波形如图7 所示。
由图7 可知,采用Z-N 法优化PI 参数的DAB变换器系统超调量σ=0.02 V,调节时间ts=6.84 ms,负载由200 Ω 突变为150 Ω 变换器的响应时间tp=7.32 ms。其超调量很小,调节时间较长,PI 调节效果不好。采用ACA 优化PI 参数的DAB 变换器σ=0.59 V,ts=5.28 ms,tp=5.85 ms。其超调量较大,有轻微振荡,调节时间较短,PI 调节效果较好。采用改进MMAS 算法优化PI 参数的DAB 变换器σ=0.01 V,ts=3.73 ms,tp=3.82 ms。其超调量较小,过渡平稳几乎没有振荡,系统响应速度较快,调节时间较短。因此,采用改进MMAS 算法优化PI 参数的DAB 变换器具有更好的动态响应。
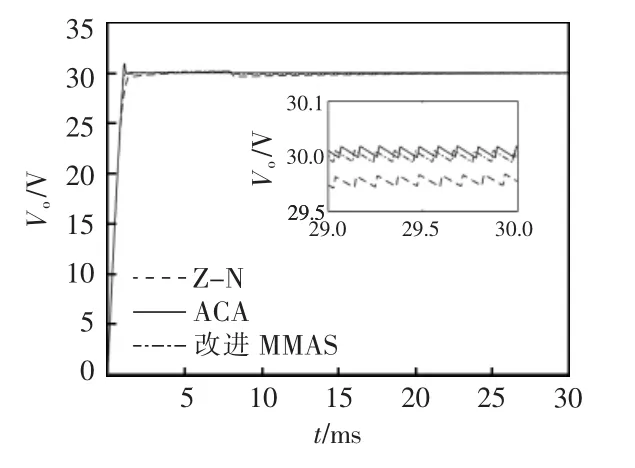
图7 DAB 变换器系统响应仿真波形Fig.7 Simulation waveforms of DAB converter’s system response
3.2 实验结果及分析
基于TMS320F28335 型DSP 控制器搭建了DAB 变换器实验样机,具体参数见表1。实际应用中,只需将样机参数代入DAB 变换器模型和算法中,即可计算出Z-N 法、ACA 和改进MMAS 算法的Kp、Ki值。3 种方法系统响应的实验波形如图8 所示,负载突变响应的实验波形如图9 所示,其PI 参数和性能指标的实验结果见表2。

图8 DAB 变换器系统响应实验波形Fig.8 Experimental waveforms of DAB converter’s system response
由图8 和表2 可知,相比于Z-N 法,ACA 和改进MMAS 算法系统响应上升速度更快,调节时间更短。由图9 和表2 可知,负载由200 Ω 突变为150 Ω 时,改进MMAS 算法优化PI 参数的DAB 变换器负载突变响应时间较短。通过对超调量、调节时间、负载突变响应时间的对比可知,改进MMAS算法对DAB 变换器PI 参数优化效果优于ACA 和Z-N 法,可使系统响应速度快、调节时间短。

图9 DAB 变换器负载突变响应实验波形Fig.9 Experimental waveforms of DAB converter’s response under load variation
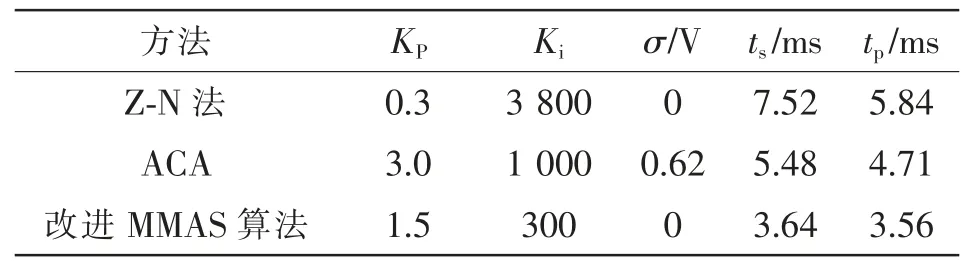
表2 3 种方法的PI 参数和性能指标Tab.2 PI parameters and performance indexes of three methods
4 结语
本文针对DAB 变换器PI 参数优化问题,提出了采用改进MMAS 算法对PI 参数进行优化的方法。通过仿真和实验,证明了相比于Z-N 法和传统ACA,改进MMAS 算法优化PI 参数的DAB 变换器具有更好的动态响应。
