织构型水润滑推力轴承软弹流润滑分析及多目标协同优化

王玉君，李强，张硕，许伟伟，唐心昊，王振波

（中国石油大学（华东） 新能源学院，山东 青岛 266580）

水润滑轴承可有效解决海洋装备润滑油泄漏导致的污染问题，进而省去了严苛的密封系统，提高了工作可靠性，因而逐渐被应用于海洋平台动力定位系统、高技术船舶推进系统等海洋工程装备中[1-3]。水的低黏度会导致轴承承载能力下降，极端工况下，会因供水不足导致轴承与轴系之间产生干摩擦，从而缩短其寿命[4-5]。

表面织构技术通过在轴瓦内表面加工具有特定分布的离散凹坑或凹槽，凭借其产生的附加微动压[6]、容纳磨屑[7]和二次润滑效应[8]，提高了轴承摩擦副的承载力，减小了摩擦系数和噪声[9]，因而可有效改善水润滑轴承摩擦表面的润滑性能[10-12]。表面织构的润滑性能与设计参数密切相关，因此织构型轴承的多参数协同优化设计研究得到了广泛关注[13-16]。Marian等[17]和Papadopoulos 等[18]研究了织构分布对推力轴承润滑性能的影响，发现局部织构分布比完全织构分布具有更好的摩擦学性能。Shinde 等[19]基于田口算法与灰色关联分析对织构型轴承进行了优化设计研究，指出提高轴承承载力的最重要因素是织构深度和分布位置。Rahmani 等[20]对平行接触副表面的方形织构进行了优化设计，结果表明，织构润滑性能对最优织构深度比的敏感性高于织构面积比，且随着织构数目的增加，敏感性差异增大。目前，对于织构优化设计的相关研究主要注重于分析织构的结构参数与分布参数对润滑性能的影响，而它们作为影响织构润滑性能的主要设计参数，其最优值之间的相互影响尚未深入开展研究。

为了提高水润滑轴承材料的减摩性、耐磨性以及抗腐蚀性，超高分子量聚乙烯、赛龙等非金属轴瓦材料逐渐得到广泛应用[21-22]。该类材料的应用与水膜厚度的减小，使得轴承的变形不可忽略[23-25]。因此，大变形下水润滑轴承的软弹流润滑性能在近些年获得广泛关注[26-27]。目前的相关研究主要围绕不同轴承材料对轴承润滑性能的影响展开，而基于软弹流润滑模型下织构型非金属推力轴承的多目标协同优化研究尚未深入开展。

为此，本文首先建立了4 种不同非金属材料的织构型水润滑推力轴承的软弹流润滑模型，研究了不同轴承材料对织构型水润滑轴承润滑性能的影响。其次，采用响应曲面与非支配排序遗传算法（NSGA-II）相结合的多目标协同优化方法，以承载力最高和摩擦力最低为目标，对织构深度及织构分布覆盖率进行了优化设计，分析了不同轴承材料对最优织构参数的影响，研究了织构最优结构参数与分布参数之间的相互作用关系。通过对织构型水润滑推力轴承的弹流润滑性能分析及多目标协同优化，为水润滑推力轴承的优化设计和工程应用提供参考。

1 计算模型

1.1 几何模型

本文以12 瓦局部织构型水润滑推力轴承为研究对象，轴承上表面为旋转圆形止推环，下表面为静止织构型扇形瓦块，织构形状采用圆形织构。轴承瓦块结构如图1 所示，具体结构参数见表1。本文所述的织构覆盖率定义为织构分布角度与平面瓦块区域角度的比值，即织构覆盖率ηcov=αt/αb。

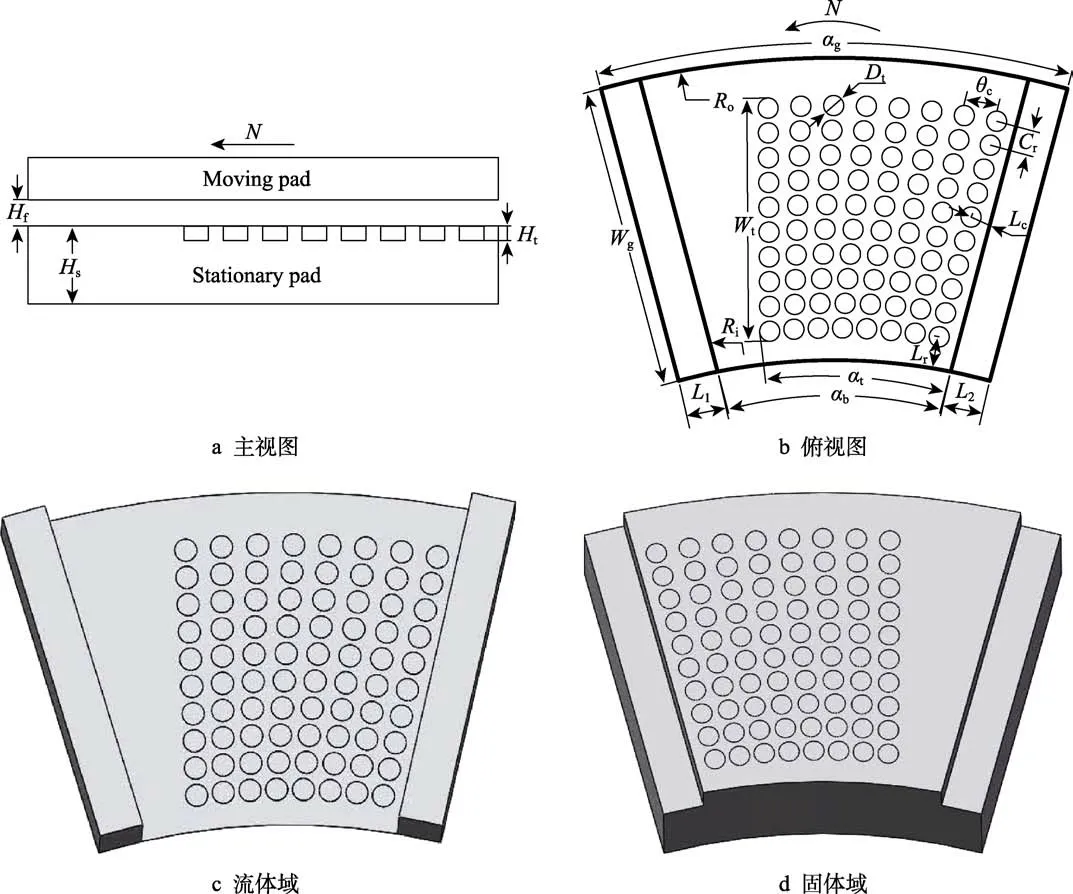
图1 织构型推力轴承瓦块结构Fig.1 Schematic of a textured thrust bearing pad: (a) Lateral view, (b) Top view, (c) Fluid domain, and, (d) Solid domain

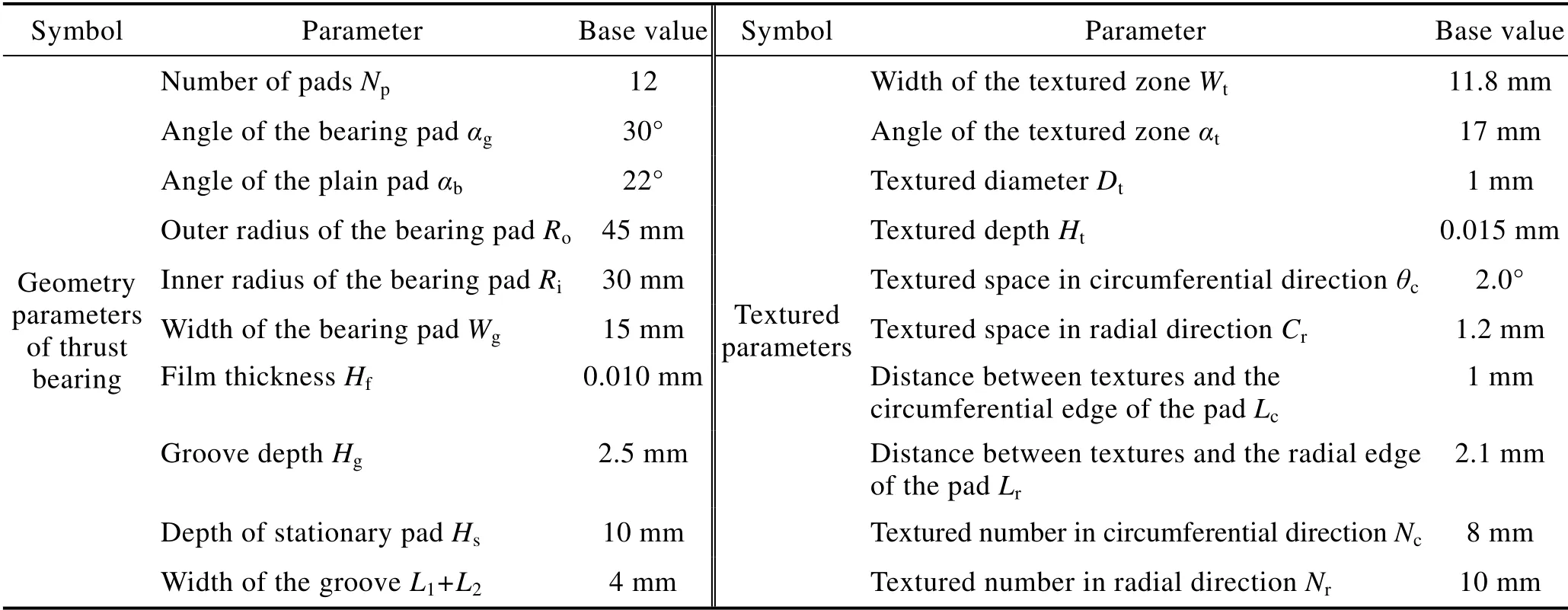
表1 织构型推力轴承结构参数Tab.1 Structural parameters of textured thrust bearing

1.2 边界条件

边界条件设置如图2 所示，润滑介质水从轴承内侧进入，从轴承外缘流出，左右进出口采用周期性边界条件，在上壁面的旋转作用下形成动压，其余壁面采用静止无滑移边界条件。具体边界条件及润滑介质参数见表2。

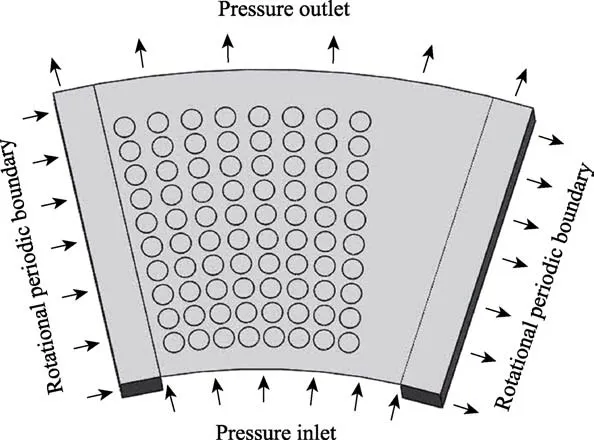
图2 边界条件设置Fig.2 Setting of boundary conditions

表2 边界条件及介质参数Tab.2 Boundary conditions and lubricant properties

2 控制方程

2.1 基本流动控制方程

轴承内部流动假设为层流流动，并将水作为不可压缩牛顿流体处理。考虑到黏性产热较少，忽略黏温效应。基本流动控制方程包括连续性方程和动量方程：

式中：mμ为气液两相动力黏度；p为流体微元体上的压力；Sv→为动量源项。

2.2 空化模型

织构型推力轴承中，发散楔结构导致该处润滑流场的压力骤降，使得润滑流场成为多相流场。利用蒸汽传输方程确定气相的体积分数：

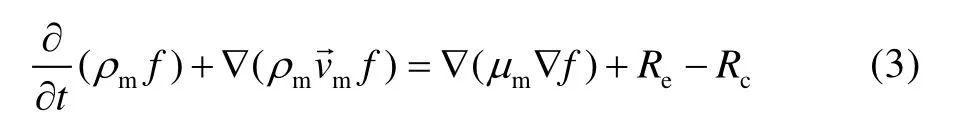
式中：f为气相水的质量分数；Re和Rc分别为气相水产生和溶解的速率。根据Re和Rc计算方法的不同，可以分为不同的空化模型。本文采用适用于水润滑推力轴承计算的Zwart-Gerber-Belamri 空化模型[28]：

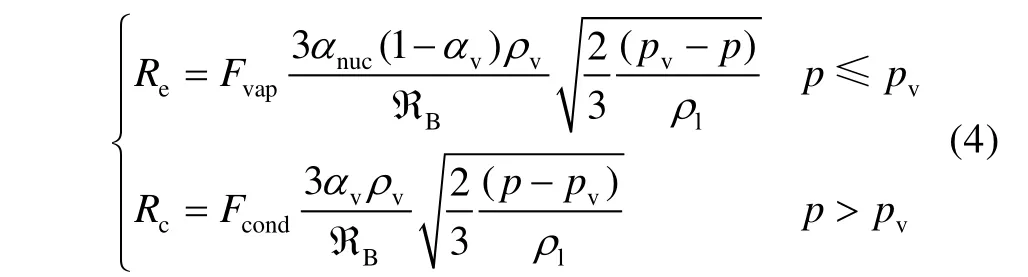
式中：αnuc为形核点的体积分数，一般取5×10–4；RB为气泡半径，一般取10–6；Fvap为蒸发系数，Fcond为凝结系数，一般取Fvap=50，Fcond=0.01；下标l 和v分别代表液态和气态介质。

2.3 流固耦合控制方程

固体变形控制方程为：

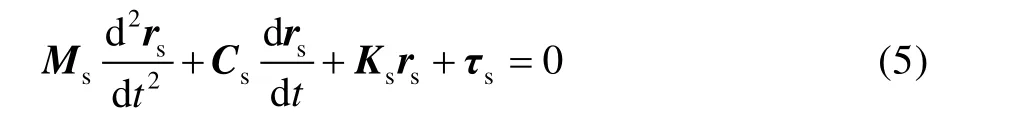
式中：Ms为固体质量矩阵；Cs为阻尼矩阵；Ks为刚度矩阵；rs为固体位移；τs为固体受到的应力。

在流固耦合交界面，应满足流体和固体应力及位移变量的守恒，即应满足如下方程：

式中：n为交界面法向量；rf和τf分别为流体的位移和应力。

2.4 优化控制方程

一个具有m个目标、n个变量和k个约束条件的多目标优化问题可以用下列方程表示：

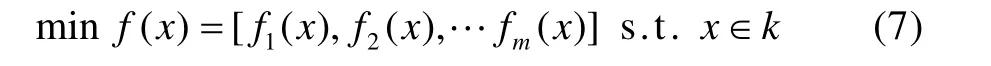
式中：f1(x),f2(x),…,fm(x)为目标函数变量；x为由自变量构成的向量，即设计变量；k为设计变量的约束集合，表示为式(8)。

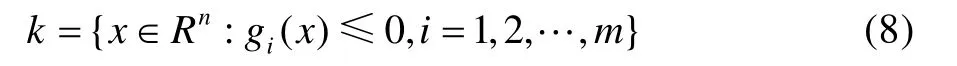
式中：gi(x)为设计变量的约束条件。

在多目标协同优化体系中，通常要涉及多目标协调问题，尤其是在一部分或全部目标及约束条件相互冲突时。本文采用非支配排序遗传算法（NSGA-II）解决上述目标冲突问题。该算法基于快速非支配排序方法和精英保留策略，通过重复迭代获得最优解，使得计算复杂性明显降低，尤其适合处理目标个数较少（即m≤3）的情况[29]。NSGA-II 的计算流程如图3所示。

图3 NSGA-II 计算流程Fig.3 Calculation flow chart of NSGA-II

3 结果及分析

3.1 模型有效性验证

为了验证本文求解方法的可靠性，采用文献[30]中的推力轴承和工况条件进行建模，采用本文的求解方法进行离散计算，并将计算结果与文献中的试验结果进行对比，结果见表3。可以看出，本文的求解结果与试验结果具有较好的一致性，说明了本文计算方法的准确性和有效性。

3.2 软弹流润滑分析

以织构覆盖率为80%、织构深度为0.015 mm 的织构型水润滑推力轴承作为基础模型，研究了碳化硅陶瓷、尼龙、超高分子量聚乙烯及赛龙等4 种不同非金属材料轴承的软弹流润滑性能。根据文献[31-32]中的水润滑轴承材料性能参数，4 种轴承材料的具体参数见表4。不同材料轴承内的压力分布如图4 所示，固体域变形如图5 所示。在基础模型中，随着轴承材料弹性模量的减小，轴承内最高压力值降低，最大变形逐渐增大。由于织构的压力累积效应，最高压力区出现在有无织构的分界处，对应的最大变形亦出现在该处。同时，在轴承入口处的外径侧存在较为明显的变形，原因是由于轴承的旋转作用引起的离心力及导水槽入口处流动面积的突然缩小，使得润滑介质水在此处堆积，进而产生局部高压区。轴承具体润滑性能参数对比见表5，随着轴承材料弹性模量的降低，轴承承载力与摩擦力均呈现降低趋势，且承载力在不同轴承材料下的变化幅度较为明显，而摩擦力无明显变化。

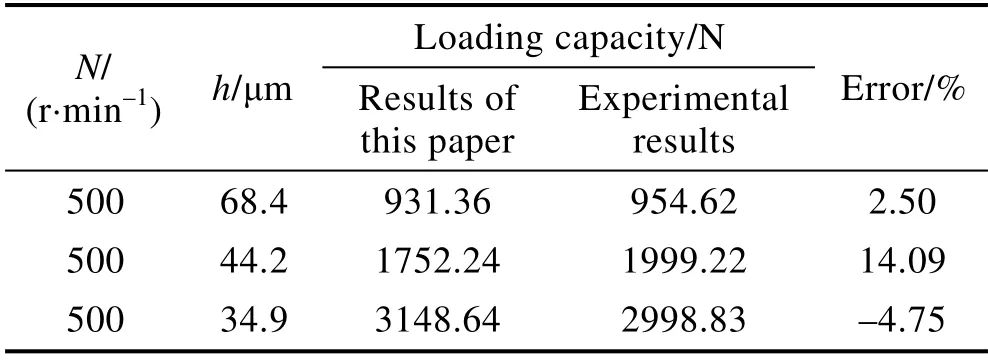
表3 承载力试验验证对比Tab.3 Experimental verification of loading capacity

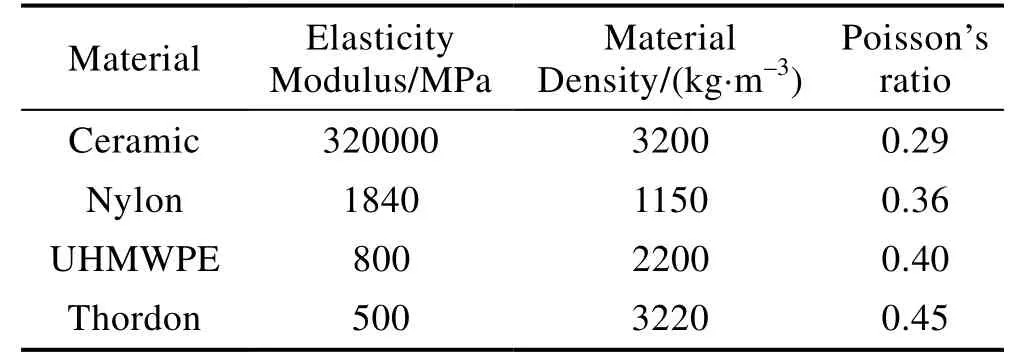
表4 轴承材料及材料参数Tab.4 Bearing’s materials and their properties

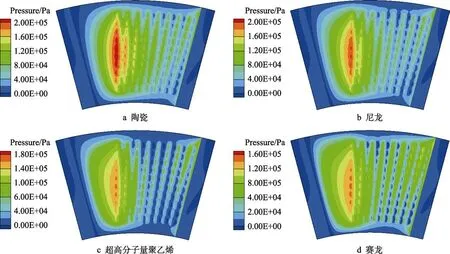
图4 不同轴承材料下流体域压力分布Fig.4 Pressure distributions of fluid domain under different bearing materials: a) Ceramic; b) Nylon; c) UHMWPE; d) Thordon

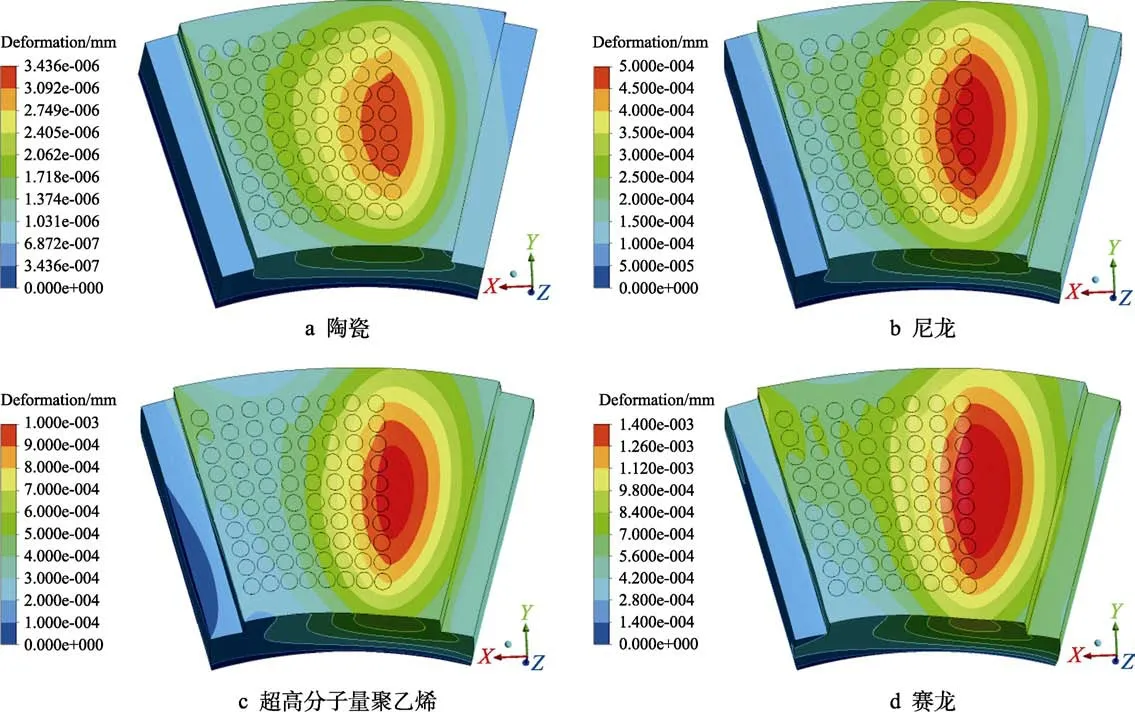
图5 不同轴承材料下固体域变形Fig.5 Deformation of solid domain under different bearing materials: a) Ceramic; b) Nylon; c) UHMWPE; d) Thordon

表5 不同轴承材料下的润滑性能Tab.5 Lubrication performances under different bearing materials

3.3 多目标协同优化

3.3.1 试验点设计

为了使得织构型水润滑推力轴承的润滑性能最优，以承载力最高和摩擦力最低为目标，对织构参数进行多目标协同优化。首先，根据文献[19]选取织构深度与织构覆盖率为设计变量，通过中心复合设计方法，对几何模型进行参数化处理，确定优化范围内试验点的位置，并对各试验点的承载力与摩擦力进行计算。每种轴承材料下各产生了40 个试验设计点。中心复合方法是试验点设计过程中最常用的方法之一，适用于校准二次响应模型，可有效提高响应曲面对各试验点的拟合度。考虑到织构常用尺寸及物理限制，设计参数基础值及优化范围见表6。

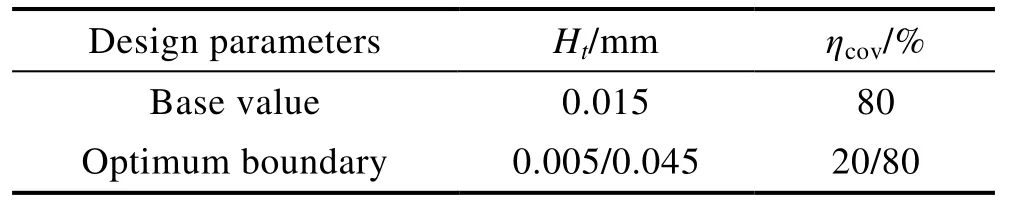
表6 设计参数的优化范围Tab.6 Optimum boundary of design parameters

3.3.2 响应曲面分析

响应曲面法以各试验设计点求解的目标参数值为基础，在不需要完全求解的情况下，即可快速地给出设计空间中所有点的目标参数近似值。本文利用多元回归分析方法拟合出承载力和摩擦力的二阶多项式响应曲面，以描述轴承润滑性能与织构深度及织构覆盖率之间的关系，并利用F检验法对各回归项进行显著性检验。承载力和摩擦力与设计参数之间的响应曲面关系如图6、7 所示。可以看出，随着织构深度及织构覆盖率的增加，轴承承载力变化较为明显，而摩擦力变化幅度较小，且不同轴承材料下，承载力随织构深度及织构覆盖率的变化趋势存在明显差异。

由图6 可知，轴承承载力对织构设计参数较为敏感。为此，以承载力为主要性能指标，研究了不同轴承材料对最优织构参数的影响，及织构最优结构参数与分布参数之间的相互影响关系。首先分析了轴承材料对最优织构覆盖率的影响，不同材料轴承承载力随织构覆盖率的变化如图8 所示。可以看出，对于碳化硅陶瓷和尼龙等弹性模量较大的轴承材料，随着织构覆盖率的增加，相同深度下，轴承承载力呈现出先上升、后下降的趋势；对于超高分子量聚乙烯和赛龙等弹性模量较小的轴承材料，随着织构覆盖率的增加，相同深度下，轴承承载力只呈现出下降趋势。因此，随着轴承材料弹性模量的减小，织构覆盖率的最优值逐渐减小。

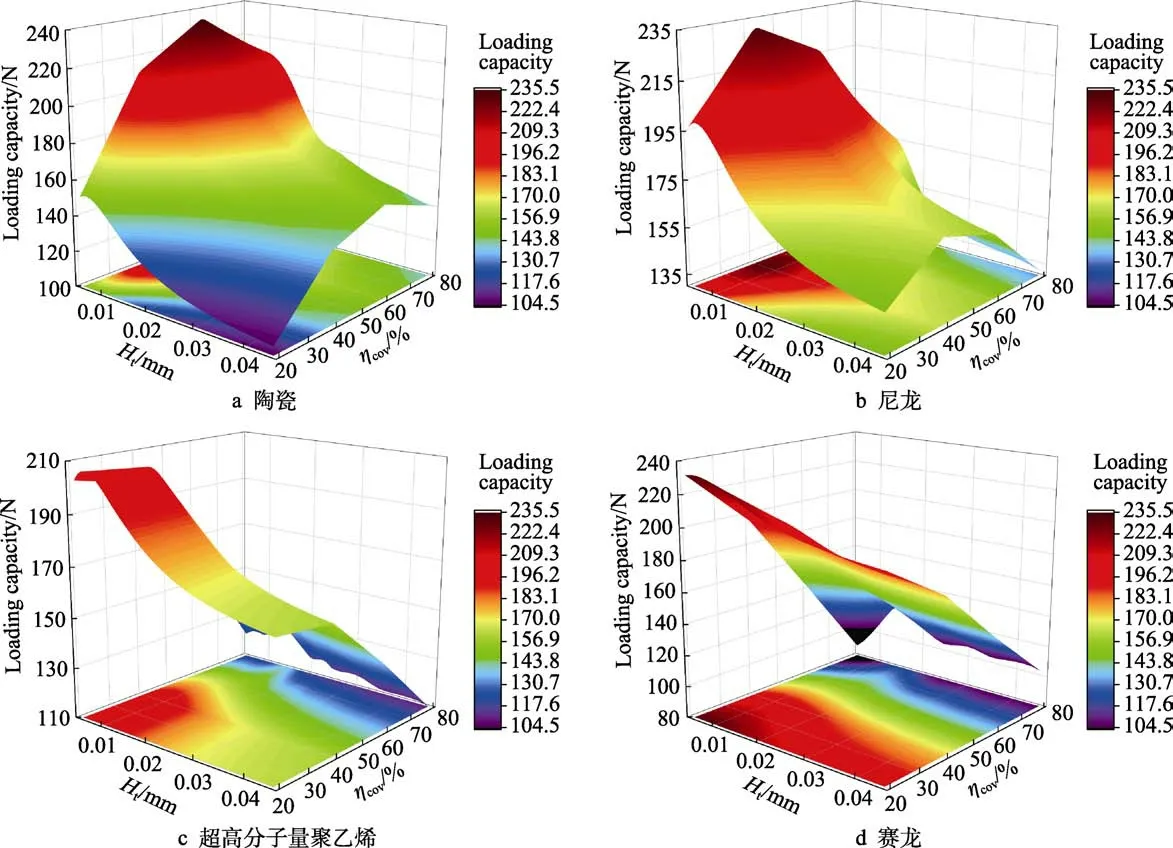
图6 不同轴承材料下承载力与设计参数之间的响应关系Fig.6 Response relationship between loading capacity and design parameters under different bearing materials: a) Ceramic; b)Nylon; c) UHMWPE; d) Thordon

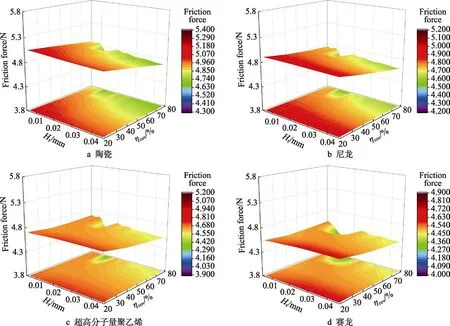
图7 不同轴承材料下摩擦力与各设计参数之间的响应关系Fig.7 Response relationship between friction force and design parameters under different bearing materials: a) Ceramic; b) Nylon;c) UHMWPE; d) Thordon

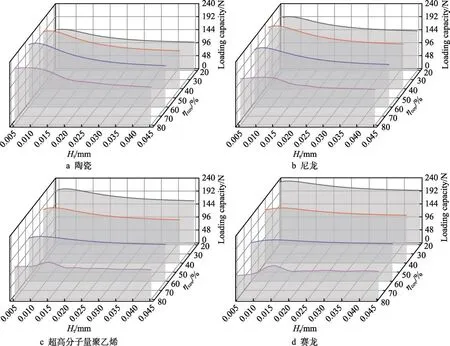
图8 不同轴承材料下织构覆盖率对承载力的影响Fig.8 Effect of textured coverage rate on loading capacity under different bearing materials: a) Ceramic; b) Nylon; c) UHMWPE;d) Thordon

为了分析不同轴承材料对最优织构深度的影响，给出了不同材料轴承承载力随织构深度的变化（如图9 所示）。可以看出，对于不同材料的织构型推力轴承，随着织构深度的增加，其承载力均呈现出先上升、后下降的趋势。当织构覆盖率为20%时，不同轴承材料下的最优织构深度值相近。当织构覆盖率增至40%及以上时，最优织构深度值随着轴承材料弹性模量的降低而逐渐增加。

为了研究织构设计参数之间的相互影响关系，以赛龙材料为例，给出了织构覆盖率与织构深度之间的关系，如图10 所示。可以看出，在同一轴承材料下，随着织构覆盖率从20%增加至80%，最优织构深度值逐渐增加。因此，相同轴承材料下，织构覆盖率越大，对应的最优织构深度值越大。综上所述，轴承材料对织构最优参数有明显影响，随着轴承材料弹性模量的降低，最优织构覆盖率逐渐降低，最优织构深度逐渐增大。同一轴承材料下，最优织构覆盖率与最优织构深度之间相互影响。

3.3.3 多目标协同优化

在上述响应曲面的基础上，以承载力最高和摩擦力最低为目标，采用NSGA-II 算法对织构深度与织构覆盖率进行了多目标协同优化。经过优化，4 种不同轴承材料下织构深度及织构覆盖率的最优值见表7。可以看出，在每种轴承材料对应的最优覆盖率下，最优织构深度值相近，而随着轴承材料弹性模量的减小，最优织构覆盖率逐渐减小。

优化前后的润滑性能参数对比见表8。可以看出，经过对不同轴承材料下织构深度及织构覆盖率的优化设计，轴承承载力大幅度提升，摩擦力无明显升高，润滑性能总体明显改善。随着轴承材料弹性模量的降低，承载力提升幅度越来越明显。优化后，不同轴承材料下流体域的压力分布如图11 所示。随着轴承材料弹性模量的降低，轴承内最高压力逐渐降低，但高压区面积逐渐增大。在最优织构参数的基础上，一方面，轴承材料弹性模量的降低会减弱轴承内的最高压力，进而降低轴承承载力；另一方面，轴承材料弹性模量的降低又会导致轴承内部高压区面积增大，进而改善轴承承载力。因此，轴承材料对承载力的影响主要取决于上述两者之间的权衡。对于碳化硅陶瓷和尼龙等弹性模量较大的轴承材料，优化后，轴承内流体最高压力明显提升，但高压区面积无明显变化；对于超高分子量聚乙烯和赛龙等弹性模量较小的轴承材料，优化后，最高压力无明显变化，但高压区面积明显增大。

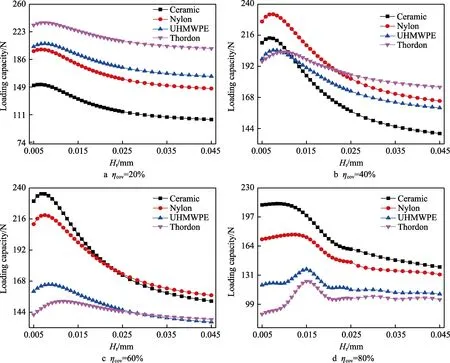
图9 不同轴承材料下织构深度对承载力的影响Fig.9 Effect of textured depth on loading capacity under different bearing materials

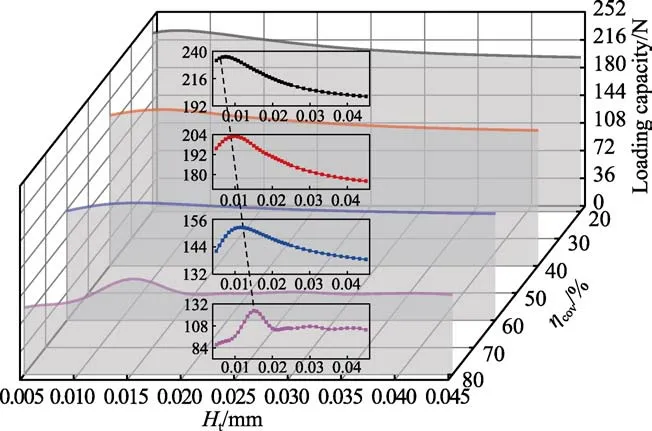
图10 织构覆盖率-深度的关系Fig.10 Textured coverage rate -depth diagram

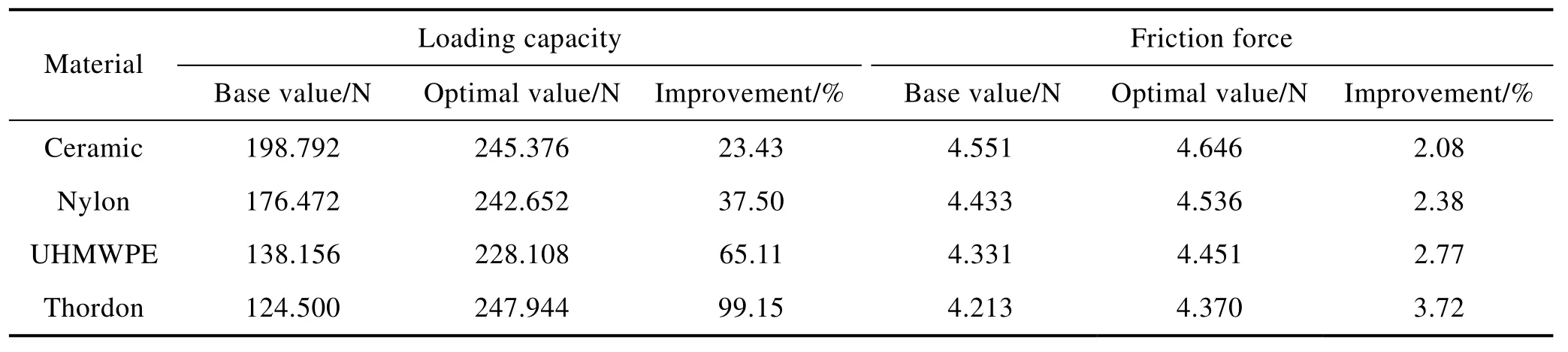
表8 优化前后润滑性能参数对比Tab.8 Comparison of lubrication performances before and after optimization

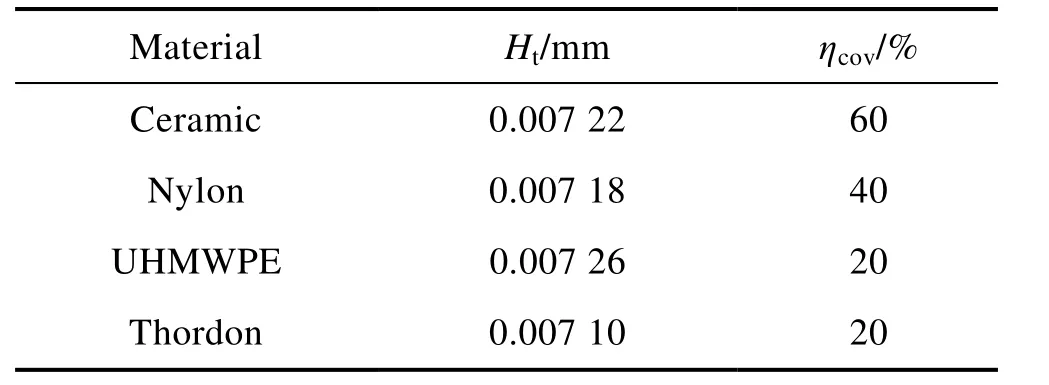
表7 不同轴承材料下设计参数的最优值Tab.7 Optimal values of the design parameters under different bearing materials

4 结论

1）采用CFD-FSI 方法建立的软弹流润滑模型，可有效预测织构型水润滑推力轴承的润滑性能，且发现轴承材料对织构型水润滑推力轴承弹流润滑性能有明显影响，表现为随着轴承材料弹性模量的降低，轴承内最高压力值逐渐降低，最大变形逐渐增加。

2）基于上述模型，结合响应曲面分析，发现随着轴承材料弹性模量的降低，最优织构覆盖率值逐渐减小。在低织构覆盖率下，轴承材料的变化不会对最优织构深度值产生明显影响，而在高织构覆盖率下，最优织构深度随着轴承材料弹性模量的降低而逐渐增加。在同一轴承材料下，织构最优设计参数之间相互影响，随着织构覆盖率的增加，最优织构深度值逐渐增大。

3）经过对织构深度及织构覆盖率的多目标协同优化，轴承承载力明显提高，润滑性能明显改善，说明NSGA-II 算法适用于织构型水润滑推力轴承的优化设计。同时发现，对于碳化硅陶瓷和尼龙等弹性模量较大的轴承材料，优化后，轴承内流体最高压力明显提升；对于超高分子量聚乙烯和赛龙等弹性模量较小的轴承材料，优化后，高压区面积明显增大。