基于整数线性规划模型的磁共振设备使用精细化管理

刘振临，栾笑笑，田 金，许 锋

（北京大学第三医院医学工程处，北京100191）

0 引言

随着医疗设备技术的飞速发展和患者对高水平医疗技术需求的不断增长，医院配备的大型医疗设备（甲、乙类）越来越多，其在医院固定资产所占比重也越来越高。2018年10月，国家卫生健康委员会相继颁布了《大型医用设备配置许可管理目录（2018年）》和《2018—2020年大型医用设备配置规划》，提出在大型医用设备的管理过程中应“逐步落实简政放权，下放审批权限，依托循证依据及时动态调整大型医用设备管理品目，逐步完善管理机制，强化事中事后监管，实施全程管理”[1-2]。我国大型医疗设备管理制度不断完善的过程呈现以下趋势：管理制度从整体框架型细化为根据设备标准的精细化管理型；配置标准下放，既注重成本控制，又注重提高大型医疗设备的使用效率；大型医疗设备配置数量逐步增加，注重医疗机构的区域功能定位[3]。

大型医疗设备的精细化管理是不断改善医疗服务的保障。目前大型医疗设备精细化管理的研究多集中于配置规划、维护保养、绩效评估等方面[4-5]，使用过程多为临床医师凭借主观经验进行管理，引入的科学管理方法较少，且很少引入数学模型对使用效率进行评估。以磁共振设备为例，目前北京大多数三甲医院的磁共振设备每天的检查时间超过12 h，个别医院的设备甚至每天运转20 h，但磁共振检查的预约等待时长仍超过1个月，严重影响了患者的就医体验，因此，如何减少患者预约等待时间，提高设备的使用效率是亟待解决的痛点问题。以北京市某大型三甲医院为例，该院磁共振检查预约等待时间长达2个月，设备每天扫描时长超过12 h，严重影响了医院的服务效率。本文通过引入整数线性规划模型，对该院5台磁共振设备的使用情况进行分析和优化改进，大幅提高了该院磁共振设备的检查效率，对科学管理大型医疗设备具有一定的指导意义[6]。

1 研究方法

1.1 线性规划的基本理论

线性规划模型是运筹学的重要分支，已经逐步成为科学化管理的重要辅助工具。其主要是在一系列背景条件的约束下，通过给定的资源条件和数据，运用模型求解，科学地给出最优化解决方案及资源配置方法[7-9]。以磁共振检查为例，如何合理安排每月预约检查人次、规划每台设备检查的部位及人次以实现检查效率的最大化，这些都是与线性规划相关的问题。通过建立线性规划模型对预约患者进行统筹安排，以减少患者预约等待的时间，提高设备的使用效率，对于指导大型医疗设备的合理配置规划也具有一定意义[10]。

线性规划问题的核心即在满足线性约束条件的前提下，使线性目标函数达到最优值（最大值或最小值）[10]。线性约束条件可以用一组线性等式或线性不等式来表达，目标函数用于衡量方案的优劣。根据线性规划的定义，线性规划问题即求取自变量x={x1，x2，…，xn}的值，使得线性目标函数在约束条件下达到最小值或最大值[11]。一般线性规划问题的标准型为

式中，xj≥0，j=1，2，…，n。c1，c2，…，cn；a11，a12，…，a21，a22，…，amn；b1，b2，…，bm与待解决的科学问题密切相关，为已知常数项[12-14]。

在实际应用中，自变量所受到的限制条件就是它本身的约束条件。当目标函数为线性函数、约束条件为线性等式或不等式时，称此数学模型为线性规划模型；当自变量限制为整数时，则称之为整数线性规划函数。单纯形法是求解线性规划问题的通用方法[15]，其求解步骤如下：

（1）找出初始可行基，确定初始基可行解，建立初始单纯形表。首先建立约束方程的系数矩阵：

式中，P1~P5为一组初始可行基。然后建立单纯形表结构，详见表1。表1中，XB为基变量，对应公式（1）中x1，x2，…，xn；CB列为基变量的常数项系数，对应公式（1）中c1，c2，…，cn；b列为约束方程组右端的常数，对应公式（2）中b1，b2，…，bm；θ列的数字是在确定变量后，按比值θ规则计算后填入。

表1 单纯形表结构

（2）计算检验各非基变量xj的检验数σj：

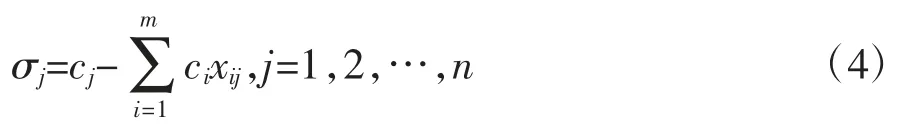
若σj≤0，则已得到最优解，停止计算；否则进入下一轮，直到获得最优解为止。

1.2 整数线性规划模型在磁共振检查中的应用

磁共振成像目前已经成为常规的医学检测手段之一，在脑成像、软组织成像等多方面有着很大的优势。但与CT相比，磁共振扫描时间较长，每天检查的患者数量有限。本文研究的目的是在保证磁共振设备检查人次及检查质量的前提下，合理分配每台磁共振设备检查人次及检查部位，以获得最佳的设备使用效率。以北京市某大型三甲医院为例，收集该院5台磁共振设备2019年11月的检查数据。其中，每台磁共振设备配置了不同的脉冲线圈，可用于不同部位的磁共振成像检查，每台设备可检查的身体部位详见表2。

表2 每台磁共振设备可检查的身体部位

分别从医学影像传输系统和数据采集系统中调取每台设备2019年11月的检查数据，得到每台设备每个部位的检查人次及平均扫描时间，详见表3。通过对每台设备相同部位检查的人次和扫描时间进行统计分析，得到5台磁共振设备11月的总扫描时间，其中，核磁一室扫描时间为1 098 842.21 s，核磁二室扫描时间为819 115.49 s，核磁三室扫描时间为1 119 013.72 s，核磁四室扫描时间为1 078 622.52 s，核磁五室扫描时间为1 119 340.49 s。

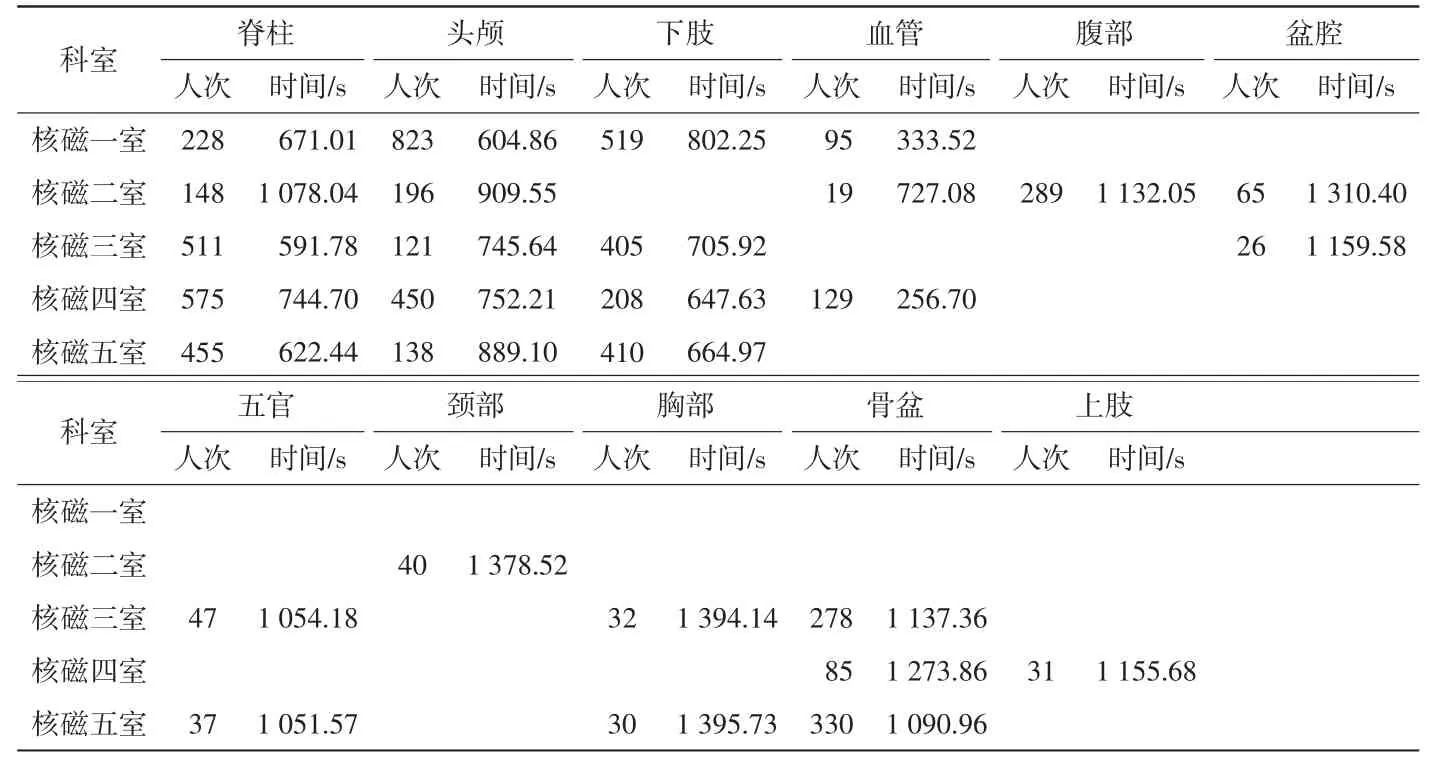
表3 每台磁共振设备每个部位的检查人次及平均扫描时间

在保证患者检查人次、检查部位不变的基础上，重新合理安排每台设备检查人次和检查部位，以实现扫描时间的最小化。首先列出目标函数和约束条件，目标函数为该月所有磁共振设备的总扫描时间：

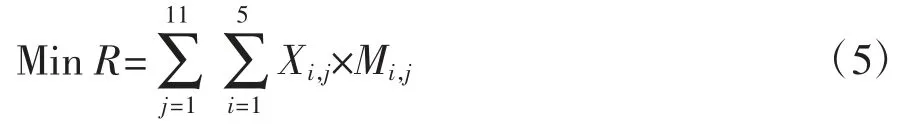
约束条件为

式中，i为核磁室数；j为检查部位；Mi，j为核磁i室检查j部位的平均扫描时间，为已知常数；Xi，j是未知数，为核磁i室检查j部位的人次数，为约束条件之一，Xi，j≥0，且均为整数。

2 结果

利用单纯形法进行最优解的计算，得到目标函数的最优解,扫描总时间由优化前的5 234 934.43 s减少到4 702 053.59 s。在检查人次不变的情况下5台设备扫描的总时间比优化前节省了532 880.84 s，检查效率有了大幅度提高，约为10.18%。

各核磁室优化前后的检查人次和扫描时间对比详见表4，相比优化前，优化后最大的特点是一些部位的检查集中到了1台或几台效率较高的设备上。优化后，核磁一室只进行头颅的扫描，扫描时间减少了53 644.13 s（缩短4.88%），检查人次增加了63人次（提高3.78%）；优化后核磁二室只进行腹部及颈部扫描，扫描时间减少436 812.24 s（缩短53.33%），检查人次减少了428人次（降低56.54%）；核磁三室只进行脊柱、盆腔的扫描，扫描时间减少了956.36 s（缩短0.09%），检查人次增加了382人次（提高26.90%）；核磁四室只进行下肢、血管、上肢的扫描，扫描时间减少了1 201.78 s（缩短了0.11%），检查人次增加了308人次（提高20.84%）；核磁五室只进行脊柱、下肢、五官、胸部、骨盆的扫描，扫描时间缩短了40 266.33 s（缩短3.60%），检查人次减少了325人次（降低23.21%）。

从结果分析来看，将整数线性规划模型引入磁共振设备的精细化管理中是合理、有效的。优化后的结果主要呈现出3个特点：（1）各设备检查部位的一致性良好。各设备检查的部位并未超出自身检查范围，这表明模型合理有效。（2）单台设备的检查部位减少。5台设备检查的部位均有所减少，每种部位的检查均集中到某一两台设备上，其中核磁一室、二室最为明显。优化后单位时间内扫描人次有所增加，设备使用效率明显提高。（3）整体检查时间缩短。每台设备的总扫描时间均有所减少，其中核磁二室最为明显，扫描时间节省了436 812.24 s，如果该时间用于腹部检查，该月可多检查385人次。

通过对2019年11月的检查数据进行分析，制订并实施了包括调整部分设备检查部位等优化措施，12月核磁共振平扫检查人次增加了343人次，效率提高了5.10%，初步显示出调整后的部分成效。

3 讨论

在实际临床工作中，磁共振设备的检查人次和检查部位多为医生凭借临床经验主观分配，每台设备检查的部位类型较多，分布比较分散，使用效率有限。本文将整数线性规划模型引入磁共振设备使用的精细化管理中，实现了磁共振设备使用效率的量化分析，对于科学管理磁共振设备的使用有着重要的指导意义。通过采用整数线性规划模型进行优化，磁共振设备使用效率大幅提高，达到10.18%。在患者预约管理中，可根据预约患者的数量进行提前建模，依据目标函数的最优解，安排每台设备检查的人次和部位，大幅度增加单位时间内检查的人次，从而缩短患者的预约等待时长。与磁共振设备类似，CT、加速器等大型医疗设备也存在数量较多、日常使用主要凭经验管理的现状，可引入整数线性规划模型进行评估管理。而且在整数线性规划模型建立后，大型医疗设备的绩效评估也可从传统的单机成本绩效分析转为某一类设备整体的绩效分析，为探索、建立更为全面的绩效评价模型提供新的手段。下一步研究中，还应考虑设备的故障率、患者的上下床时间、急诊磁共振检查的非预约人次增加、增强型磁共振扫描（扫描过程中需注射造影剂）等多个影响因素，引入更多、更有效的数理模型，不断推进大型医疗设备精细化管理的发展。