一种高计算收敛性的粗糙曲面三维形貌模型
2021-06-04乔泽龙韩炬董威
乔泽龙,韩炬,董威
(华北理工大学机械工程学院,063210,河北唐山)
所有的工程表面都具有一定的粗糙性,适宜的粗糙面模型应用在相关研究中能有效降低试验成本并提高分析效率,对于深入理解结合表面之间的接触[1]、磨损[2]、润滑[3]、热传导[4]等机理具有重要的意义。国内外学者研究粗糙面模型的构建已有五十几年[5],主要涉及两个关键问题,其一是微凸体高度及分布情况能客观反映实际粗糙面形貌特征,其二是微凸体接触模型能有效反映实际接触变形规律。本文重点关注粗糙曲面三维形貌特征模型的构建。
机械加工面的粗糙形貌与加工工艺密切相关,近年来,众多学者结合刀具尺寸与倾角、加工路径以及振动等因素,实现了对机械加工工件表面形貌的预测[6-7],但一般用于工件表面质量评测,没能应用于机械结合面的接触、润滑、磨损等特性分析。
现有获取粗糙面的三维形貌主要包括试验法与数值法两种方式。目前,表面形貌的测试方法很多[8],但受到横纵坐标分辨率的限制,测试获取的形貌模型在很多细节上被简化,此外测试得到的模型只是对现有加工面的再现,很难对获取改性的曲面形貌进行对比研究。
通过分析真实粗糙表面数据,发现粗糙表面具有统计自仿射的特性[9-10],进一步研究证实粗糙表面的分形特性与尺度无关[11]。虽然应用数值方法构建三维粗糙曲面的方法很多,但由于分形粗糙面在进行接触、润滑等分析时有较高的适用性[12-16]。周超等利用W-M分形函数合成粗糙表面在速度、精度以及合成表面的均方根偏差等方面均有一定优势[17]。因此,本文基于分形理论表征粗糙表面微凸体高度及分布特性,并在粗糙面模型中综合体现曲面的宏观轮廓与微观形貌。黄健萌等在对纳观粗糙表面的建模研究中发现了分形表面不连续的问题,并选择适合通带的高斯滤波器处理数据,获得了较为理想的仿真粗糙面,滤波处理后的表面数据在进行数值分析时,计算收敛性有显著提升[18]。
本文综合应用微分几何理论与分形理论,构建能表征复杂形状曲面的宏观轮廓与微观形貌的三维模型,通过对模型进行平滑处理,提升了模型在诸如接触、疲劳、润滑等数值分析时的收敛性。
1 机加工粗糙曲面表面形貌模型
1.1 二维粗糙分形形貌表征的W-M函数
一般应用W-M函数为[19]对粗糙面微观形貌进行分形模拟。W-M分形函数具有连续、处处不可导和自仿射的特点,表达式为
(1)
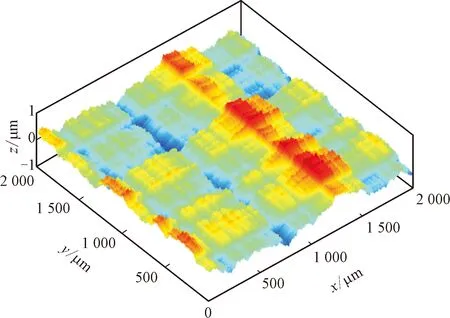
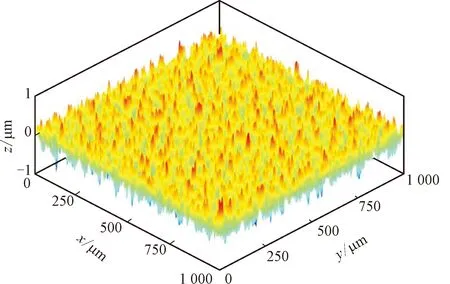
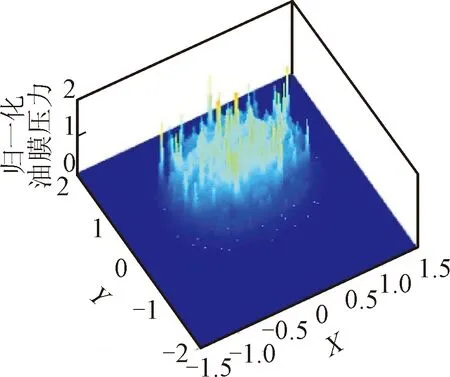
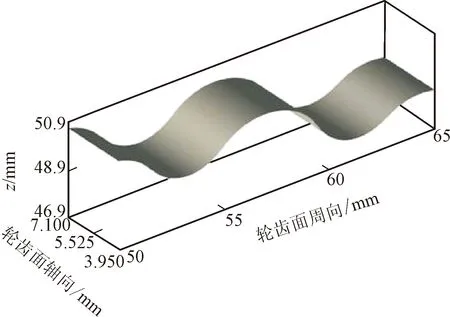
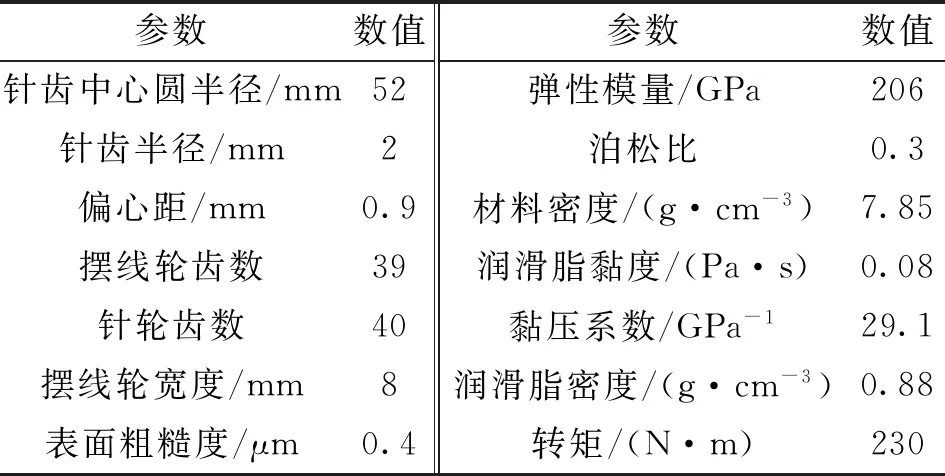
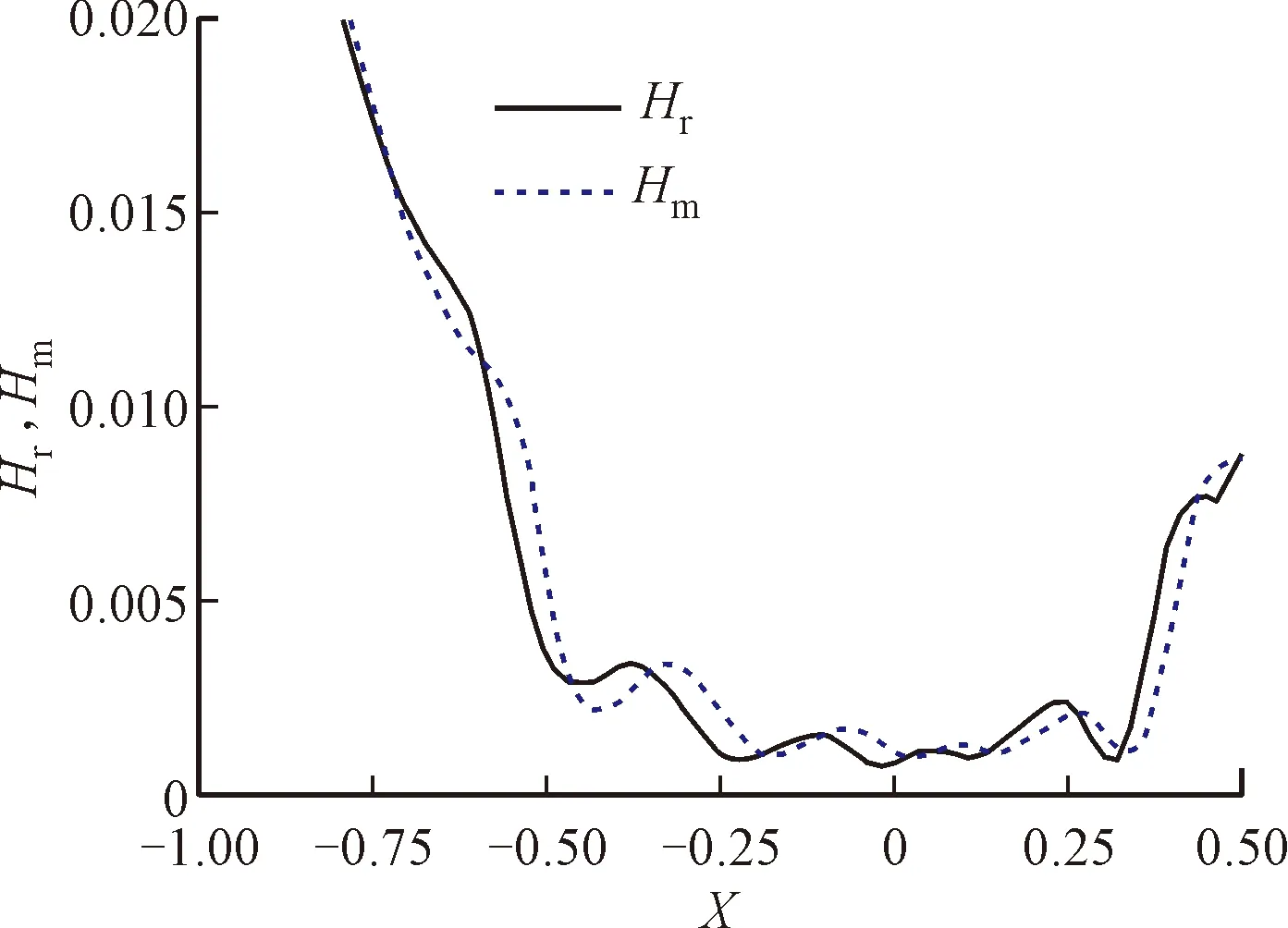
式中:G为特征尺度,表征分形粗糙峰谷高度;γ为粗糙曲面的空间频率,一般取γ=1.5;n为空间频率指数;D为分形维数,二维分形模拟时D值取(1 W-M函数用于表达二维工程粗糙表面时,一般取式(1)的实部,Majumdar和Bhushan根据式(1)进一步提出了M-B函数[20],表达式为 (2) M-B函数可以表征二维分形曲线,但机械结合面接触、摩擦、疲劳、润滑等研究的重点集中于面接触问题,且工程中粗糙表面呈各向异性或各向同性,因此需要构建粗糙表面的三维形貌模型。 通过二维W-M函数表达式,把x与y方向的W-M分形叠加在一起,实现x、y两向异性的三维分形粗糙面,公式如下 (3) 式中:z(x,y)为的三维粗糙表面轮廓幅值;Gx、Gy表示x、y方向的二维尺度系数;Dx、Dy表示x、y方向的二维分形维数;γ为空间频率,取值1.5;nmin为最低频率阶数;nmax为最高频率阶数。若分形函数曲面尺寸为L×L,取样长度L内应至少包含最低频率成分一个波长,则最低空间频率γnmin>(1/L),则有nmin=lg(1/L)/lg(γ);若取样间隔为Ls,根据奈奎斯特采样定理,最高空间频率为γnmax<(1/2Ls),则有nmax=lg(1/2Ls)/lg(γ)。 式(3)中,x和y方向分形函数各空间频率信号分量初始相位默认为0。实际应用中,若各频率成分初相位为0,叠加后会导致曲线起始段出现翘起的边缘效应。为避免边缘效应,引入随机相位φnx和φny,取值范围[0,2π],其含义为对应空间频率γn信号分量的随机相位,公式为 (4) 分别基于随机相位和0相位生成分形曲线,为了作图清晰,空间频率阶数n取1~12。如图1所示,图1a、1b中分形曲线各频率成分初相位为0,曲线起始值随n增加而增加,曲线具有边缘效应,曲线前端呈现出翘起状态;图1c、1d中分形曲线各频率成分具有不同的初相位时,曲线边缘效应消除。 (a)0相位时的空间频率分量幅值 表示各向同性三维分形粗糙面的W-M函数[17]如下 (5) 式中:h(x,y)为粗糙面微凸体高度;D为分形维数(2 根据式(4),可得各向异性三维粗糙仿真曲面,如图2所示,其中x和y方向特征尺度系数和分形维数相同,特征尺度系数取Gx=Gy=1.36×10-5mm,分形维数分别取Dx=1.488,Dy=1.518。采样长度为2 mm,采样间隔为1 μm,则nmax=33,nmin=16。图3为各向异性粗糙面在x方向和y方向的截面曲线。 图2 各向异性分形粗糙面Fig.2 Anisotropic fractal rough surface 图3 各向异性粗糙面x和y方向截面曲线Fig.3 Cross-section curves of anisotropic rough surface in x- and y-direction 根据式(5),可得到图4所示的各向同性三维粗糙仿真曲面,取样参数与各向异性相同,G=1.36×10-5mm,D=2.8。图5为各向同性粗糙面在x方向和y方向截面分形粗糙轮廓曲线。 图4 各向同性分形粗糙面Fig.4 Isotropic fractal rough surface 图5 各向同性粗糙面x和y方向截面曲线Fig.5 Cross-section curves of isotropic rough surface in x- and y-direction 分形粗糙表面具有处处连续但不可微的特点,其轮廓放大时在更小尺度上仍然呈现出自仿射的粗糙特征,其上任一点的斜率都不存在,曲面形态表现为尖锐毛刺。分形函数获得的粗糙表面直接用于接触等数值分析计算时运算收敛困难,有时在迭代计算初期出现发散现象,需要进行平滑滤波,才能进行后续的分析计算。若将不连续特征视为形貌叠加噪声的结果,采用低通滤波器对分形粗糙面数据进行空间滤波去噪处理,可平滑形貌毛刺,从而获得微观平滑的形貌数据。分形函数高频成分会产生在微观层次游离出表面的孤立物质(原子团),采用高斯滤波平滑可以消除由分形特性引起的不合理数据[18],但仍能保留模拟数据的分形特征。 图6 高斯滤波后各向同性粗糙面Fig.6 Isotropic rough surface after Gaussian filtering 图7 高斯滤波后各向同性x和y方向截面曲线Fig.7 Cross-section curves of isotropic rough surface in x- and y-direction after Gaussian filtering 采用高斯滤波对分形粗糙形貌高度进行平滑时,中心位置点高度为包括本点在内的邻域各位置高度数据按高斯分布规律的加权和,在实现对数据平滑的同时,能够保留形貌高度的原始总体分布特征。二维高斯滤波器的核心为高斯二维卷积算子,本文选取高斯核为9×9,σ=1.8。 将本文生成的分形粗糙数据,应用于二维点接触弹流润滑分析,对滤波前后的仿真计算进行对比。仿真节点数N=130,载荷w=105N,接触球体半径为0.02 m,最大赫兹接触压力为0.9 GPa,初始黏度为0.05 Pa·s。为了节约计算时间,将收敛相对精度设为两次迭代,各节点油膜压力之和相差小于1.6×10-4N。仿真计算结果如图8和图9所示,通过滤波前后压力两次迭代油膜压力差的变化情况可以看出,滤波后迭代过程加快将近一倍,原始数据迭代136次耗时11 475 s,滤波后数据迭代69次耗时6 419 s。归一化油膜压力分布如图9a所示(X、Y为x、y方向归一化长度),由于原始数据中存在高频细节,油膜存在大量尖锐压力峰值。工程实际中,工件表面在初期刚体接触时尖锐微凸体会首先发生塑性变形[23-24],因此在弹流润滑工况下,图9b所示的滤波后油膜分布更符合实际情况。 图8 高斯滤波前后粗糙面点接触弹流润滑仿真Fig.8 Elastohydrodynamic lubrication simulation of rough surface point contact before and after Gaussian filtering (a)原始数据仿真 虽然机械动态结合面的结合区很小,接触瞬时的曲面可以近似为粗糙平面,这是众多粗糙面模型将接触区简化为平面接触的重要原因。但结合面宏观轮廓,如齿轮齿廓、凸轮轮廓等,在传动过程中对传动性能有关键影响,因此三维粗糙曲面的形貌模型应该综合体现曲面的宏观轮廓与微观形貌,即将体现微观形貌的W-M函数与体现宏观形貌的矢量函数叠加。 本节以RV减速器中摆线轮轮齿齿廓为例,创建三维粗糙曲面模型。RV减速器摆线针轮啮合接触属于柱面接触,摆线针轮接触仿真计算需要基于摆线轮曲面构建粗糙曲面,由光滑曲面与非均匀的微凸体叠加构成粗糙曲面形貌模型,其中光滑曲面由矢量函数表示,微凸体的高度值由W-M函数计算,微凸体高度方向为相应曲面点的法矢量方向。摆线轮齿的粗糙表面可表示为摆线轮齿齿面的矢量函数和粗糙面矢量函数之和。 二维摆线轮廓函数矢量平面曲线公式为[25] r(θ)=x(θ)i+y(θ)j,r(θ)∈C0 (6) 式中:i和j为坐标轴向的单位向量;x(θ)和y(θ)为摆线轮廓函数如下 (7) (8) (9) 式中:K1=e/Rg;γ0=jθ,θ为滚圆滚角;e为基圆和滚圆中心距。 用曲线弧长代替式(2)中的x为自变量,可得 (10) 式中:h(s)为分形粗糙形貌轮廓高度;s为沿齿廓曲线的弧长,其他参数同式(2)。摆线轮齿廓弧长为 (11) 粗糙齿廓曲线的二维矢量方程为摆线轮轮齿齿廓矢量方程和微凸体高度矢量之和,公式为 r*=r(θ)+h(s)m(θ) (12) 式中:r(θ)为摆线齿廓曲线矢量;m(θ)为曲线点法向单位矢量,m(θ)表示式为 (13) 利用式(12),在Matlab中可生成如图10所示的二维粗糙轮齿齿廓。 图10 粗糙齿廓矢量曲线Fig.10 Rough surfaces and vector end curves 为便于数值计算,基圆和摆线矢量方程可变形为欧拉公式形式,基圆矢量方程为 (14) 摆线矢量方程为 (15) 修形后的摆线轮齿的齿廓矢量方程可转化为 (16) 利用式(10)~(16)可实现摆线轮齿的齿廓建模,如图11所示。摆线轮半径为52 mm,针齿半径为2 mm,偏心距为0.9 mm,摆线轮齿数为39,等距修形量、移距修形量分别为-0.01 mm和-0.012 mm。摆线轮齿分形粗糙齿廓建模如图12所示。 图11 矢量法生成摆线轮齿的齿廓 Fig.11 Profile of cycloid gear tooth generated with vector method 图12 矢量函数合成摆线轮齿粗糙齿廓曲线 Fig.12 Rough profile curve of cycloid gear tooth synthesized by vector function 摆线轮齿齿廓三维建模的核心问题是如何将理论光滑齿轮曲面模型与粗糙面模型相结合。粗糙面建模可依据式(4)和式(5)获得模型数据,并采用二维高斯滤波对数据进行平滑。理论齿廓三维建模可采用圆柱坐标矢量函数,获得齿廓三维曲面,再通过数值计算获得曲面上点的单位法向矢量。各曲面法向矢量以粗糙曲面相应点高度值为模长,获得粗糙曲面矢量矩阵,理论齿面矢量与粗糙曲面矢量之和即为粗糙齿廓的矢量模型。 摆线轮三维齿廓在圆柱坐标系中的矢量方程为 (17) 式中:z为齿廓轴向坐标,其他参数与式(16)相同。得到的摆线理论齿廓三维模型如图13所示。 图13 摆线理论齿廓三维模型Fig.13 3D model of cycloid tooth profile 在齿面法向单位矢量计算中,由于曲面z方向的导数为0,故法向矢量表达式为 (18) 求得曲面法向矢量如图14所示。 图14 齿廓曲面和法向矢量Fig.14 Tooth profile surface and normal vector 摆线轮齿粗糙齿廓矢量方程为 Rc(θ,z)=R(θ,z)+h(s(θ),z)mc(θ,z) (19) 式中:h(s(θ),z)mc(θ,z)为各向异性或各向同性粗糙曲面矢量。依据式(19),按经验取特征尺度系数和分形维数,采用Matlab模拟摆线轮三维粗糙齿面、各向异性和各向同性的摆线轮齿粗糙曲面分别见图15~图17。 图15 摆线轮三维粗糙齿面Fig.15 3D rough tooth surface of cycloid wheel 图16 各向同性三维粗糙面局部放大图Fig.16 Local zoom-in view of 3D isotropic rough tooth surface 图17 各向异性三维粗糙面局部放大图Fig.17 Zoom-in view of 3D anisotropic rough tooth surface 应用PS50型Nanovea三维非接触式表面形貌仪获得真实摆线轮齿面图像,如图18所示。图18a为珩磨机械加工面的微观形貌,不同方向上的微凸体分布相对平均;图18b为研磨机械加工面的微观形貌,不同方向上微凸体的分布差别较大,有明显的纹向。通过图16与图18a、图17与图18b的对比可知,构建的表面形貌模型能够比较客观地反映实际机械加工面的形貌。通过改变模型参数,可以快速得到不同的表面形貌模型,为后续的界面接触、润滑等分析提供数据。 (a)各向同性加工面 在摆线针轮传动的混合润滑分析中应用本文提出的模型进行数值计算,主要参数如表1所示。仿真分析采用朱东等开发的MixedEHL软件[26]。 表1 摆线针轮传动混合润滑分析基本参数Table 1 Parameters of cycloid-pin gears and grease 图19为应用各向异性粗糙面模型计算得到的润滑脂膜厚度及压力分布情况,网格密度为256×256。采用本文模型,能完成相应的粗糙面润滑接触计算,得到的膜厚及压力分布与实际一致,表明了模型的有效性。 (a)压力分布 (a)膜厚分布对比曲线 图20为采用实际扫描粗糙面数据与采用本文模型得到的x方向的膜厚及压力曲线,其中Hm、Hr和Pm、Pr分别为应用本文模型和实际扫描粗糙面计算得到的无量纲膜厚和无量纲压力。从图中可看出,本文模型与实际扫描粗糙面的计算结果一致,最小膜厚与最大压力误差分别为2.06%与1.08%,本文模型的计算时间为18 629.062 5 s,实际扫描粗糙面的计算时长为42 014.453 1 s,计算效率提升55.7%。此外,本文模型还可以通过修改参数,快速得到不同特征粗糙面,并进行相应的仿真对比,在实际应用中有明显的优势。 为方便对机械结合面进行相应的接触、疲劳、润滑等数值分析,本文提出了一种可以综合体现机械结合面宏观轮廓与微观形貌的三维粗糙曲面模型。该模型能客观表征任意轮廓的机械零件曲面,且能有效表征粗糙面的纹向、粗糙度等微观形貌。针对分形粗糙面模型处处不可微导致计算不易收敛的问题,采用二维高斯滤波对模型数据进行平滑处理,提高了粗糙面参与数值计算时的收敛性。本文提出的模型可以用于机械结合面的接触、润滑以及摩擦磨损分析,模型体现了结合面的宏观轮廓与微观形貌信息,可以通过对比分析,为机械结合面的设计参数、加工工艺参数等的优化提供指导。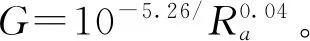
1.2 形貌各向异性和各向同性表征函数

2 三维分形形貌粗糙表面仿真
2.1 各向异性分形粗糙表面仿真

2.2 各向同性分形粗糙表面仿真


2.3 分形粗糙表面的滤波处理


3 基于W-M函数与矢量函数的形貌合成模型
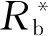

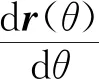

3.1 摆线针轮齿廓二维形貌建模
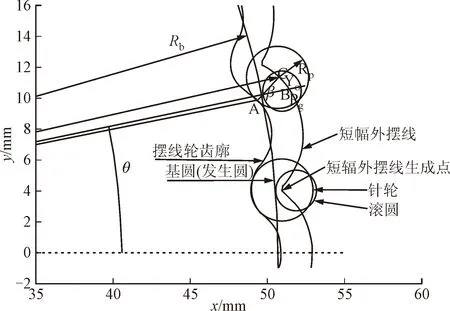

3.2 摆线轮轮齿齿廓的三维形貌建模
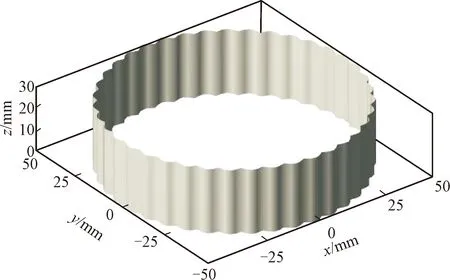


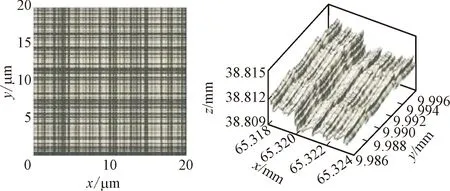

3.3 摆线针轮传动混合润滑分析算例

4 结 论
