具有参数漂移特征的高可靠产品加速寿命评估方法研究*

胡俊波 张子剑 顾奕翀 张志华

（1.海军工程大学船海院 武汉 430033）（2.天津航海仪器研究所 天津 300131）（3.上海船舶设备研究所 上海 200031）

1 引言

随着科技的发展，高性能、高可靠性产品越来越丰富，而由于性能参数漂移而引起的失效是这类产品一种重要的故障模式。为了准确有效地对这类产品的剩余寿命进行分析，需要充分利用试验数据包含的信息。目前，基于性能参数漂移的研究已成为退化产品可靠性评估的热点问题之一［1～3］。文献［4～5］将产品性能指标的退化信息转化为可靠性信息，实现产品的可靠性评估。文献［6］提出模型预测与产品寿命分布逼近相结合的方法，提高了产品剩余寿命估计的精度。许多学者还利用维纳过程建立了各种性能退化模型，分析了产品的性能退化可靠性［5，7～8］、剩余寿命预测［9］、维修策略的合理制定［10～11］等各种问题。文献［12］认为环境对产品的影响可以看成是一种冲击，并建立了基于冲击的性能退化模型。这些理论与方法或多或少存在着预测误差或分布拟合精度等问题，特别是为了进行估计需要收集多个失效样本，时间成本较高。

本文针对具有参数漂移特征的高可靠性产品，着力解决综合利用加速失效样本信息的问题，提出了一种加速寿命评估方法。首先，利用扩散理论描述产品的参数漂移规律，建立漂移模型并预测产品不同时刻的可靠度。其次，在获得样本的可靠度估计值后，用威布尔分布拟合单个产品寿命分布。再次，针对不同应力下的失效样本信息，给出加速方程估计方法，建立多应力寿命评估模型。最后，通过实例计算，验证了该方法的可行性。通过提出综合利用加速试验信息的评估方法，给出了一种高可靠产品失效样本收集困难的解决途径。

2 参数漂移的扩散模型

2.1 模型假设［4］

假设A1：产品退化量在时刻t的漂移量X(t)是独立增量过程，且X(0)=0。

假设A2：产品退化量具有远离中心位置的趋势，漂移量随机增大，偏离速度取常数a。

假设A3：产品退化量的漂移量X(t)的波动幅度随时间随机增大。取波动系数为常数b2。

2.2 漂移退化的扩散模型

因此，漂移量X(t)实际上是一个齐次扩散过程［13］。因此，当产品的漂移系数和扩散系数均为常数时，在假定X(s)=x的情况下，时刻t的漂移量X(t)（s＜t）的概率密度函数为［4］

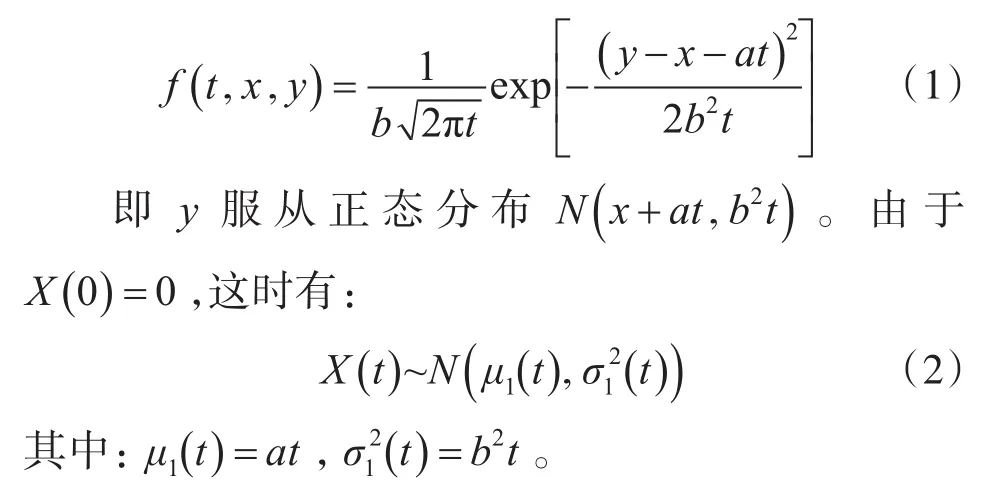
2.3 产品的退化可靠度

当参数漂移产品的退化量在阈值内变化时产品能正常工作，否则，当产品的退化量超出阈值时，产品将失效。假设退化量的的阈值上下限为Lsh，Lsl。其可靠度函数为

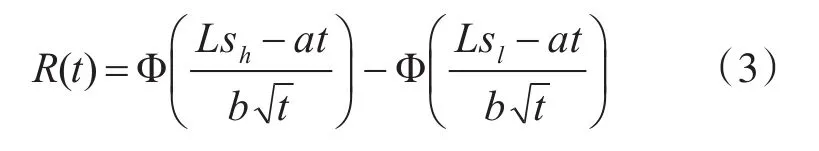
3 参数漂移模型参数估计及寿命分布逼近研究

3.1 参数估计

根据式（2）有似然函数为

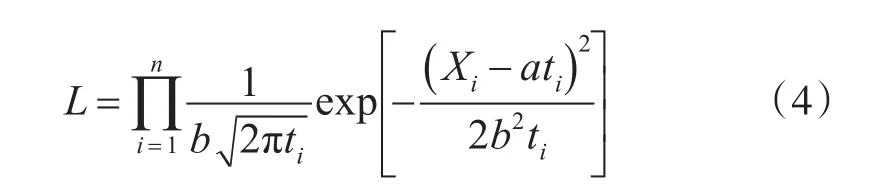
假设产品在时刻ti(i=1，2，…，n)检测得到退化量数据Xi(i=1，2，…，n)。那么有：

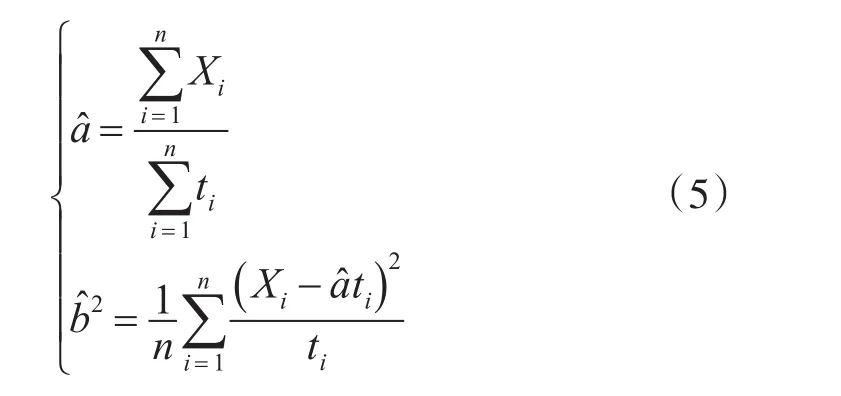
3.2 可靠性评估

在得到模型参数估计后，就可预测产品任意时刻t(＞tn)的可靠度，其预测值为

3.3 寿命分布逼近

对于一些高可靠退化产品（尤其是机电产品），其寿命可用威布尔分布来描述，那么产品的可靠度为

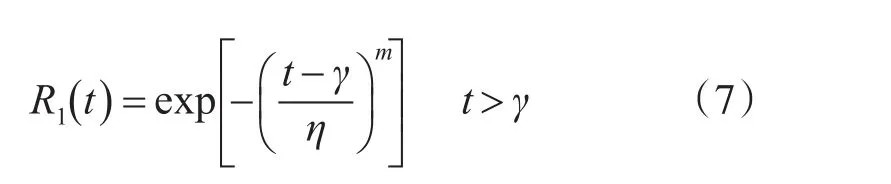
式中：γ为保证参数；m、η分别为形状参数和尺度参数。

根据式（6）可以得到单个产品在不同时刻可靠度 的 估 计 值。 令y=lnt′，μ=lnη，σ=1/m，可将威布尔分布可以转化为极值分布R2(y)，记xi=ln[-lnR2(yi)]，则在假定保证参数γ已知的情况下，利用最小二乘法可对参数μ，σ进行估计，得

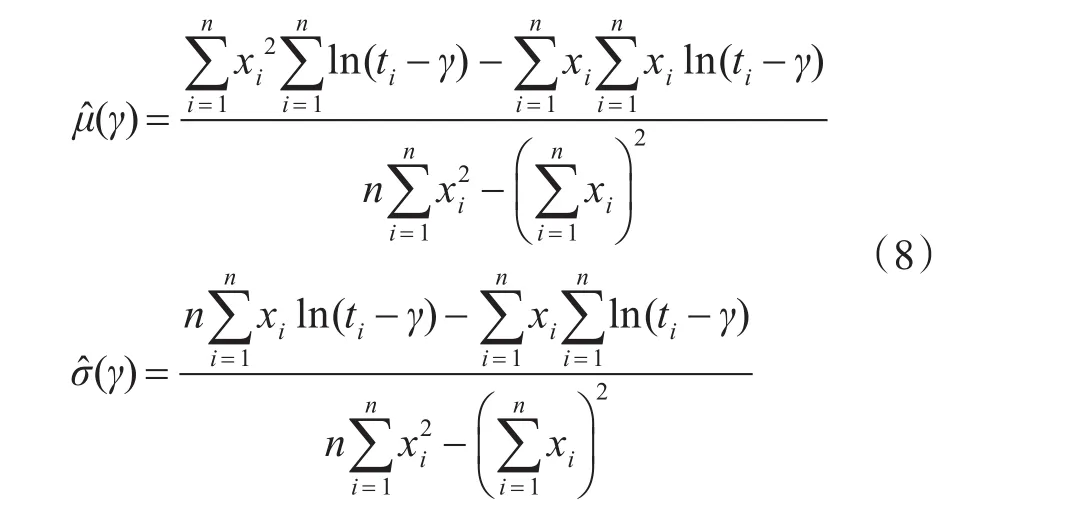
上式中，由于保证参数γ未知，实际上无法得到参数μ，σ的估计，可利用式（9）所示拟合误差最小为优化目标，搜索得到参数γ、μ、σ的估计。

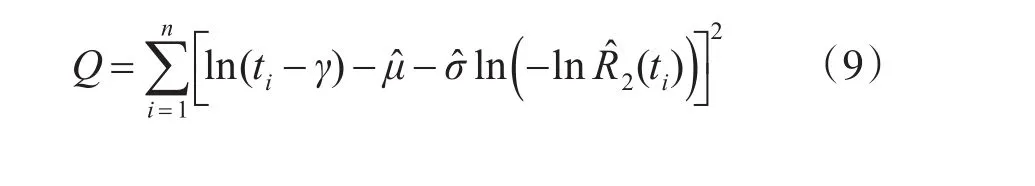
4 加速方程估计及寿命评估方法

在利用威布尔分布逼近单个产品可靠度函数并验证其贴近效果后，如果样本处于不同应力之下，则应按照相关的加速寿命试验统计方法对加速方程进行估计。

4.1 加速方程估计

在产品寿命为三参数威布尔分布的情况下，对产品实施加速试验，设选定k个加速应力水平S1＜S2＜…＜Sk和容量分别为1的k个样本，假设在加速应力水平Si(i=1，2，…，k)及正常应力水平S0下，产品满足恒加试验的基本假定［14］且寿命分布函数服从三参数威布尔分布，即：

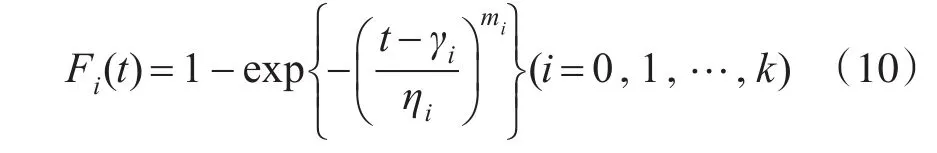
那么，加速方程的估计方法如下：

1）形状参数估计

在应力条件Si(i=1，…，k)下，利用3.3节介绍的方法计算可得到相应应力下威布尔分布参数m的估计值，那么常应力水平下的形状参数m0为

2）尺度参数估计

在应力条件Si(i=1，…，k)下，利用3.3节介绍的方法计算可得到相应应力下威布尔分布参数η的估计值η(Si)，且满足：

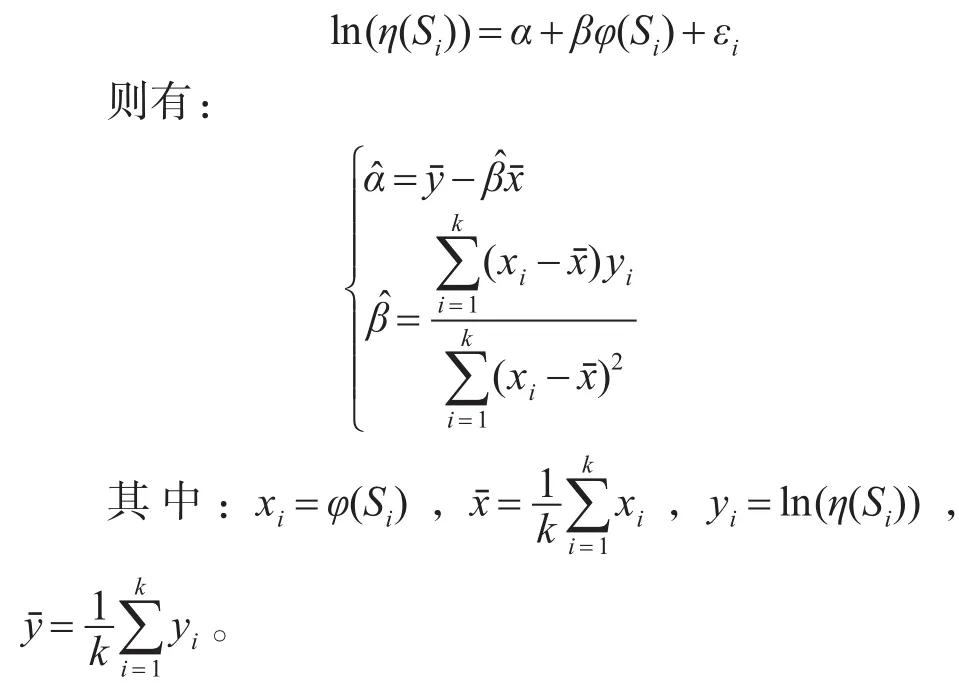
那么在常应力水平S0下，有

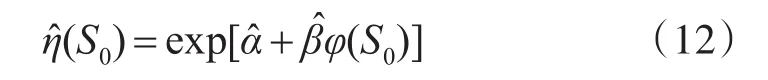
3）保证参数估计

在应力条件Si(i=1，…，k)下，计算可得到相应应力下参数γ的估计值γi，且满足：

则有：

4.2 多应力寿命预测

根据加速方程估计结果式（11）～（13），可以估计得到产品在常应力水平S0下的可靠度为

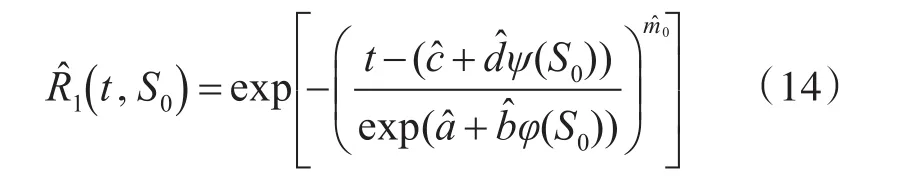
5 实例分析

某种用于测量水深的传感器，通过变送器把压力信号转化为电信号，在使用过程中，其零位电压会产生漂移，当漂移超过阈值（±40mv）时，产品失效。同时，该传感器为高可靠产品，在常应力水平下（50m水深），其第100周可靠度预测值仍在0.85以上［4］。因此，为了准确预测该产品寿命，在常应力水平下收集多个失效样本的时间成本是巨大的，考虑采用加速寿命试验收集失效样本并评估产品可靠性。

根据该产品的失效机理，选取压力作为加速应力搭建了加速寿命试验系统，通过改变作用在传感器上的压力模拟0m～1000m水深环境。此时有应力 S为压力 P（单位取 MPa），且φ(S)=ln(S)，ψ(S)=ln(S)。在加速试验方案中，共设计了五个试验样本，其加速应力分别选定为2Mpa、4Mpa、6Mpa、8Mpa、10Mpa，样本零漂电压随时间的变化曲线如图1所示。

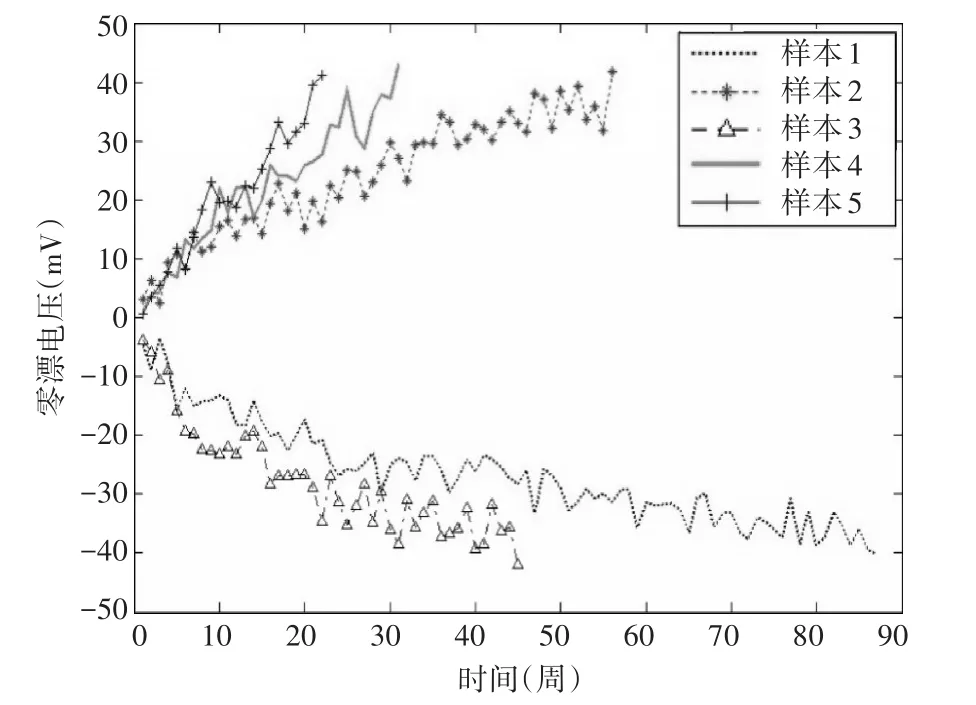
图1 传感器零位电压时历曲线

利用产品加速寿命试验数据，根据3.1，3.3节介绍的方法，可以分别估计漂移模型参数以及三参数威布尔分布的参数，如表1所示。

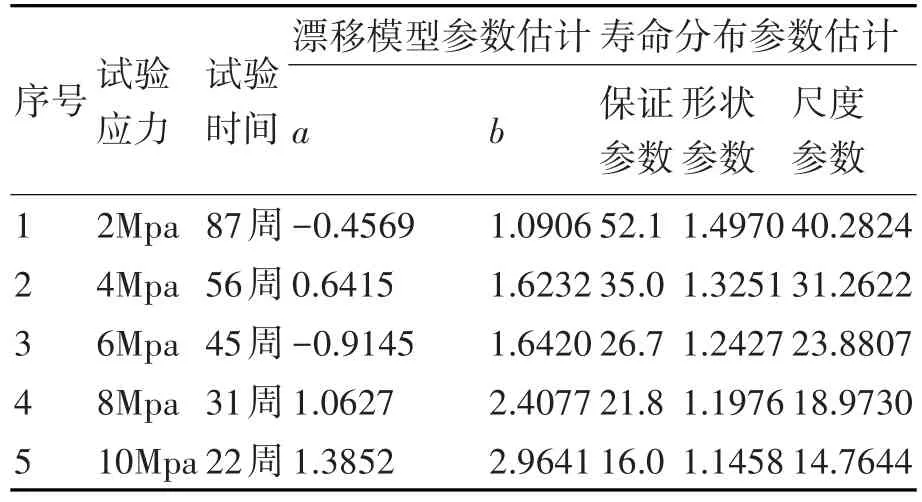
表1 各试验样本参数估计结果

利用表1的计算结果，按照4.1节介绍的方法可以估计得到加速方程相关参数：

将其作为常应力水平下产品失效时间的估计，计算可知本文方法节省了73.7%的试验时间，对于控制试验时间具有重要价值。

6 结语

本文综合利用加速失效样本信息，提出了一种适用于高可靠性产品的加速寿命评估方法，经实例分析表明该方法对于解决高可靠性能退化产品失效样本收集困难的问题具有重要的意义。但也存在一些不足，表现为尚未对评估结果的有效性进行理论证明或者仿真分析，尚未对其他基于机理的性能退化模型进行推广应用。