曲波变换结合Sobel算子的SAR图像边缘检测方法*
2021-06-04
(91388部队 湛江 524022)
1 引言
SAR图像具有复杂的边缘纹理结构以及特有的相干斑噪声,如果直接使用传统的基于一阶和二阶梯度的边缘检测算子进行边缘提取,则会产生以下两个不易解决的问题。第一为相干斑噪声属于高频图像信息,而SAR图像边缘也属于高频结构,所以使用梯度算子检测图像边缘会导致在斑点噪声处产生虚假边缘。第二为SAR图像纹理和边缘信息丰富,边缘和纹理同为高频信息结构,如果直接在SAR图像上进行梯度算子边缘提取,则会将细小的纹理信息连同边缘结构一同检测出来,从而在提取的边缘图像上会呈现出纷乱的纹理细节,导致边缘信息体现不够明显。
针对上述问题,本文提出将曲波变换作为边缘提取的预处理步骤,实验证明增加曲波预处理可以起到较为有效的作用,使其达到良好的边缘检测效果。
2 曲波变换
曲波变换(Curvelet Transform)为小波变换在图像处理领域的发展,属于多尺度几何分析[1]。小波基组成的稀疏字典在所有尺度和位置都是各向同性的,它们并不能高效率地表示诸如直线、曲线等具有各向异性性质的结构[2]。所以在多尺度几何分析领域人们发展了曲波、轮廓波、剪切波等具备各向异性和方向灵敏性的稀疏表达工具,它们在图像处理应用中取得了很好的效果[3]。
曲波字典因其多分辨率各向异性的支撑集,正是一种能够对分片光滑图像结构实施有效稀疏表达的工具[4]。其对提取各向异性结构和线性目标的边缘具有良好的适用性。
第一代曲波变换是在脊波变换的基础上进行改进的。脊波变换对于边缘为直线的结构可以高效表示,而对于曲线结构却难以稀疏地表达。针对这一问题,第一代曲波变换采用了局部区域进行脊波变换的方式,把曲线边缘结构在细分的尺度内变成了接近直线边缘的结构[5]。
第二代曲波由一系列特殊结构的支撑基所构成。母函数φj通过平移和旋转得到一组曲波基函数。曲波支撑基的有效长度和宽度服从抛物线的尺度关系[6]。
离散曲波的频率划分示意如图1所示。

图1 离散曲波变换频率划分
对示例图像进行曲波变换,结果如图2所示。
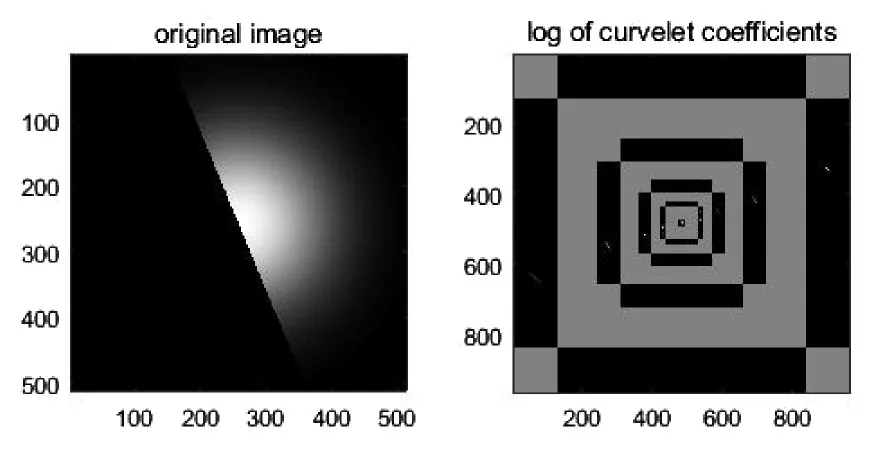
图2 曲波变换示例
在图2中,示例图像经过Curvelet变换后被划分为六个尺度层,从内到外分别为第一层到第六层,第一层为Coarse尺度层,为低频系数组成的尺度层,第六层成为Fine尺度层,为高频系数组成的尺度层,中间的第二、三、四、五层称为Detail尺度层[7],每个尺度层被分割为四个大方向,每个大方向上又被划分为8、8、16、16个小方向,每个小方向为由中高频系数组成的。Coarse层系数为低频系数,表示了图像的概貌[8],Fine层系数为高频系数,体现了图像的纹理、边缘以及噪声的信息[9],Detail层系数包含的主要为边缘特征,并且具备多方向性的表示。
3 基于曲波变换的SAR图像预处理
基于小波变换的去噪方法对于SAR图像存在一定的局限性,因为小波不具备各向异性,在对SAR图像进行二维小波变换后,边缘的系数表示并不具备稀疏性,所以要重建图像边缘就必须保留许多的小波系数[10],而Curvelet变换可以使用较少的系数大值表达图像的边缘,所以在去噪以及边缘提取上占明显优势,可以达到比较理想的效果。
本节方法为首先进行SAR图像曲波变换,根据噪声估计结果和曲波变换系数值在各个变换尺度设置合适的阈值,根据阈值处理系数,然后通过曲波逆变换得到处理后的图像。阈值为使用蒙特卡洛法计算各高频尺度上的噪声方差,而后在第各层乘以不同的比例因子作为去噪阈值。各尺度比例因子从第二层到最外层逐渐变大。
选取SAR图像示例一、示例二,分别使用中值滤波去噪、小波硬阈值去噪以及曲波变换阈值去噪方法处理,结果如图3、图4所示。

图3 SAR图像示例一去噪结果

图4 SAR图像示例二去噪结果
从上述去噪结果可以看出,中值滤波虽然去除了大部分噪声,但模糊了部分的边缘细节,小波硬阈值方法的去噪效果不够理想,经过本文曲波变换阈值去噪处理后,不仅SAR图像相干斑噪声得到有效的抑制,而且较好地保留了SAR图像边缘信息,为下一步Sobel算子边缘检测提供了比较理想的条件。
4 曲波变换结合Sobel算子的SAR图像边缘检测
图像处理中包括多种边缘检测梯度算子,常用的包括普通一阶差分,Robert算子、Sobel算子、Canny算子等,二阶差分包括拉普拉斯算子,为基于过零点检测的方法[11]。
Sobel算子是一种利用局部差分寻找边缘的算子。它考虑了图像3×3邻域的处理,Sobel算子由两个3×3的卷积核构成,分别为横向及纵向,将图像中的每个像素分别和这两个卷积核做卷积,获取在X方向以及Y方向的梯度幅值以及方向,然后经过阈值处理得到X、Y方向上的边缘图像[12]。Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘,其对噪声具有平滑作用,可以提供较为精确的边缘方向信息[13]。
在对SAR图像进行曲波去噪处理后,使用Sobel算子检测图像边缘。选择SAR图像示例一、示例二,分别使用未经过预处理的Sobel算子、经过中值滤波后的Sobel算子、小波阈值去噪后的Sobel算子以及本文方法检测边缘,结果如下所示。
分析各方法的边缘检测结果可知,在原图像上直接进行Sobel边缘检测会因为斑点噪声过多而导致边缘不够准确,并且一些地方会产生虚假的边缘。中值滤波后检测的边缘不够完整,源于其在抑噪的过程中模糊了部分的边缘细节信息。小波去噪后检测的边缘比较零散,不够连续,可以看到部分斑点噪声依然存在,这影响了检测的结果。本文方法检测的边缘比较连续,准确度比较高,并且消除了大部分斑点噪声的影响,效果突出。

图5 SAR图像示例一边缘检测结果

图6 SAR图像示例二边缘检测结果
5 结语
SAR图像斑点噪声严重、纹理边缘结构复杂,使用梯度算子直接检测边缘的效果不佳。针对上述问题,鉴于曲波变换对线性奇异性的稀疏表达,可以有效消除斑点噪声,本文提出了预先进行曲波阈值去噪而后采用Sobel算子检测边缘的方法。将本文方法与中值滤波后的Sobel边缘检测以及小波硬阈值去噪后的Sobel边缘检测两种方法做实验对比,结果表明本文方法检测的边缘更加连续和完整,效果更为理想。
