基于多循环多判断的海运装载方案建模与优化*

（陆军炮兵防空兵学院军事理论教研室 合肥 230031）

1 引言

海运装载是将需要运输的部队人员、装备和物资装载到海上运输工具的一种作战行动，该行动进行的是否合理、科学，直接影响着部队的作战效果。本文主要以装载面积为方案求解指标，以装载重量为方案评价指标，在优先单一类型装载原则的基础上，建立算法模型，提出求解海上运输工具需求量及装载方案的通用解法，即“多循环多判断装载法”。

2 海运装载方案建模

通过借助Matlab辅助工具，以装备的“装载完成率”及“利润”最大化为目标函数，以运输工具载重为限制对所求方案进行评价以及优化，以混合装备类型的装载船数量是越少越好的原则进行模型的构建［1］。

2.1 装载方案通用功能模型

按照每一种运输工具有限数量的单舰装载方案来建立输送任务的舰船装载方案模型［2］。我们假设各种运载工具的单舰装载方案为Sij，则Sij为第i型运载工具的第j种单舰装载方案，假设运输工具有14种，则各型运载工具的单舰装载方案矩阵为S：

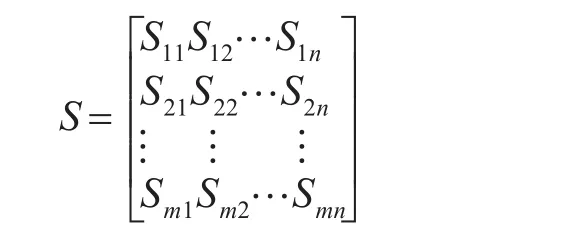
其中，i=1，2，3…m分别代表装载工具的数量，假定n代表所有类型运载工具中单舰装载方案数量最多的可能使用单舰装载方案数量，进一步假设所有运载工具可能装载方案都存在n数量的单舰装载方案，而实际上不存在的那些单舰装载方案取0即可。

而基于以上原则，优先单一类型装备进行装载，所以最终所求装载方案的结果中大多数运载工具应该装载的是同一种类型的装备；还有一小部分运载工具装载方案是多种装备的混合装载。即每种类型的运载工具中大部分最终的装载方案从这n种方案中选择，剩下的一小部分并不在这个矩阵中表示，而是采用其他算法求解出具体装载方案单独表示。装载重量和装载面积是影响装载方案的主要因素，在本模型中求解时只以面积限制作为约束，而载重限制将作为后期方案评价的元素［3］。假设登陆输送任务需要k1种装备，则其单位装载重量、单位装载面积均可由附件得出，此处写作行矢量的形式面积A和重量W：

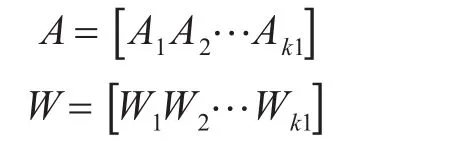
假设所需要装载的各种装备的总面积和总数量分别用ZA和ZW表示，所需要的装载k1种装备的数量可以用矩阵表示为

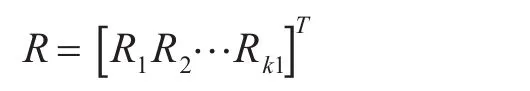
其中，k1≤14。这个矩阵中的值是由装载任务事先给定的［4］，则：

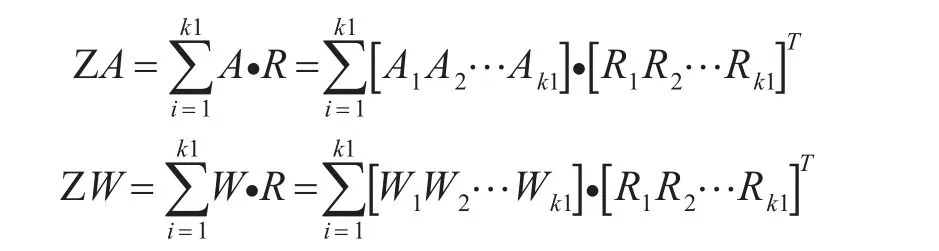
2.2 装载方案实际装载模型

假设各型运输工具的各种单舰装载方案实际需要装载k2种装备，而实际装载的种类肯定小于总的种类，即k2＜k1，只是把行矢量A和W从中截取一部分，设截取后的行矢量为A′和W′，则：

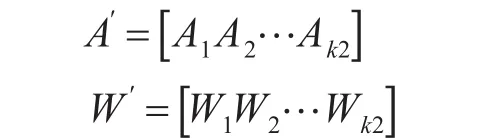
各种单舰装载方案中实际的装备数量可用R′表示如下：

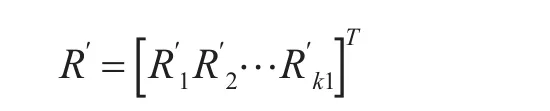
上述矩阵中的数量是各个单舰装载方案的实际数量。设每一种单舰装载方案所可以装载的总面积和总质量分别用ZA′和ZW′表示，其含义代表在该方案的装载下该运载工具可以装载装备的总面积和总质量［5］，则：

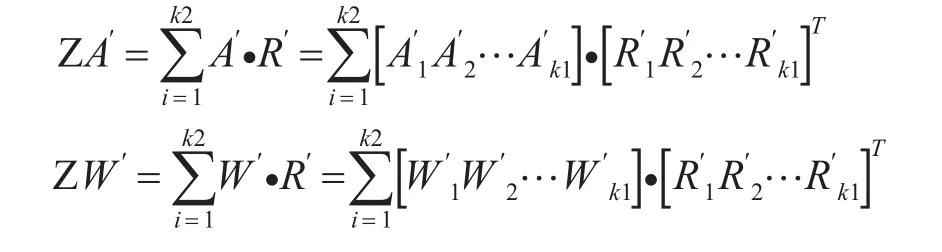
其中，ZA′和ZW′是肯定小于各个装载工具的实际装载面积和实际承载量。由于Sij是一个m×n的矩阵，所以ZA′和ZW′同样可以构成一个m×n的矩阵，表示方法与上述S相似。则最终的装载方案就可用S矩阵中各个元素的具体数值来表示，各型运载工具的单舰装载方案被实施的一次即为各型运载工具的被使用一次［6］。则整个输送任务的装载方案可以用矩阵N表示：

Nij表示整个输送任务采用运载工具单舰装载方案为Sij的数量。则此矩阵所代表的含义为其横坐标之和即为某种登陆艇的使用数量（除了混合装载的登陆艇）［7］。由此可以建立输送任务的装载方案优化模型如下表示：

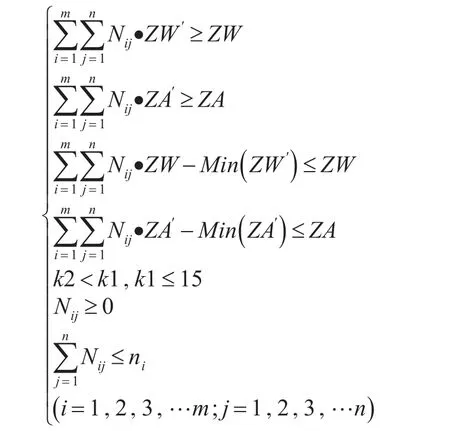
2.3 模型的设计描述

通过建立一种通用的模型可以同时求解各个类型旅的需求量。考虑到实际情况，在计算各个旅的运输工具需求时，优先将单一类型装备的所有数量或面积装载在同一艘运载工具上，同时优先同一种类型的运载工具，基于以上优先原则，以同一种装备的“装载完成率”为目标函数进行转载工具类型的选择［8］。选择后，每一种装备都会有剩余的装备，简称“装备余料”，将剩余的装备余料统一放置在“混合池”中等待分配，即下一步的装载工具选择，此时在上一步“装载完成率”最大化的条件下，装备余料将会是尽可能少的［9］。之后求解的问题是对剩下所有类型装备的装备余料进行统一装载，此时可以进行混合装载，本文将采取以用船数量最少化为目标的启发式算法进行装载工具的选择。

3 海运装载方案的多循环多判断求解思路

3.1 方法描述

求解过程采用优先单一类型装载原则的“多次循环多次判断装载法”，具体方法描述如下：以某型旅的一个旅级单位为例，假设该旅有n种装备（全服武装人员也当做一种装备），则将会循环使用该装载法n次，输入n次装备面积或数量。在为某种装备分配装载工具时是按优先级进行选择，那么按照一种优先级规则对所有类型装备进行工具分配时，装备对装载工具的选择权利是越来越小的，即可供其分配的装载工具种类和数量是随着前面的装备的装载完成而动态减少的，本文设定待装载装备的优先级规则为武装人员的优先级最高，然后按照装备的右下角角标从小到大的顺序进行装载工具的分配和选择。最后运用遗传算法和启发策略的算法设计对“装备余料”进行并行迭代，从而求得最优解［10］。

3.2 求解步骤

具体思路及多循环多判断装载法的结构图，如图1所示。

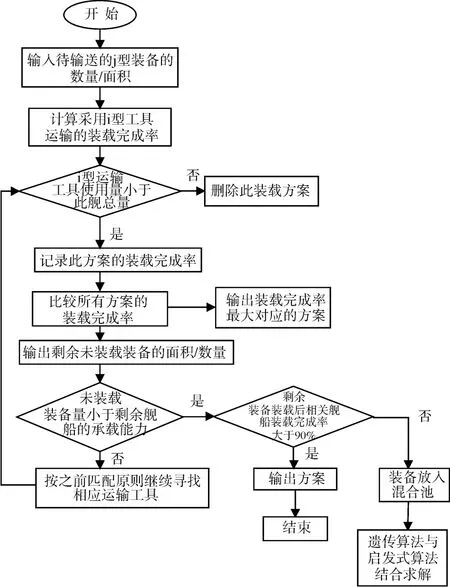
图1 多循环多判断装载法结构图

从运算的具体步骤可以看出，实际上从Step4开始又是类似于Step1的初始输入的循环，以此进行反复运算，最终得到最优方案［11］。也就是说，同一类型装备最多需要两种装载工具即可满足优先单一类型装载原则，并且满足装备余料最少的约束条件。

4 运载方案的实例运用

海上运输是保障部队进行跨区训练人员装备运输投送的重要方式，只有精准高效的运输才能够使部队快速到达集结地域，顺利完成训练任务。本文以I型旅的运载需求为例，运用本文中运载方案的模型，阐述问题的求解步骤。

4.1 基本数据情况

表1为I型旅的输送任务，表2为各类型运输工具的装载能力。

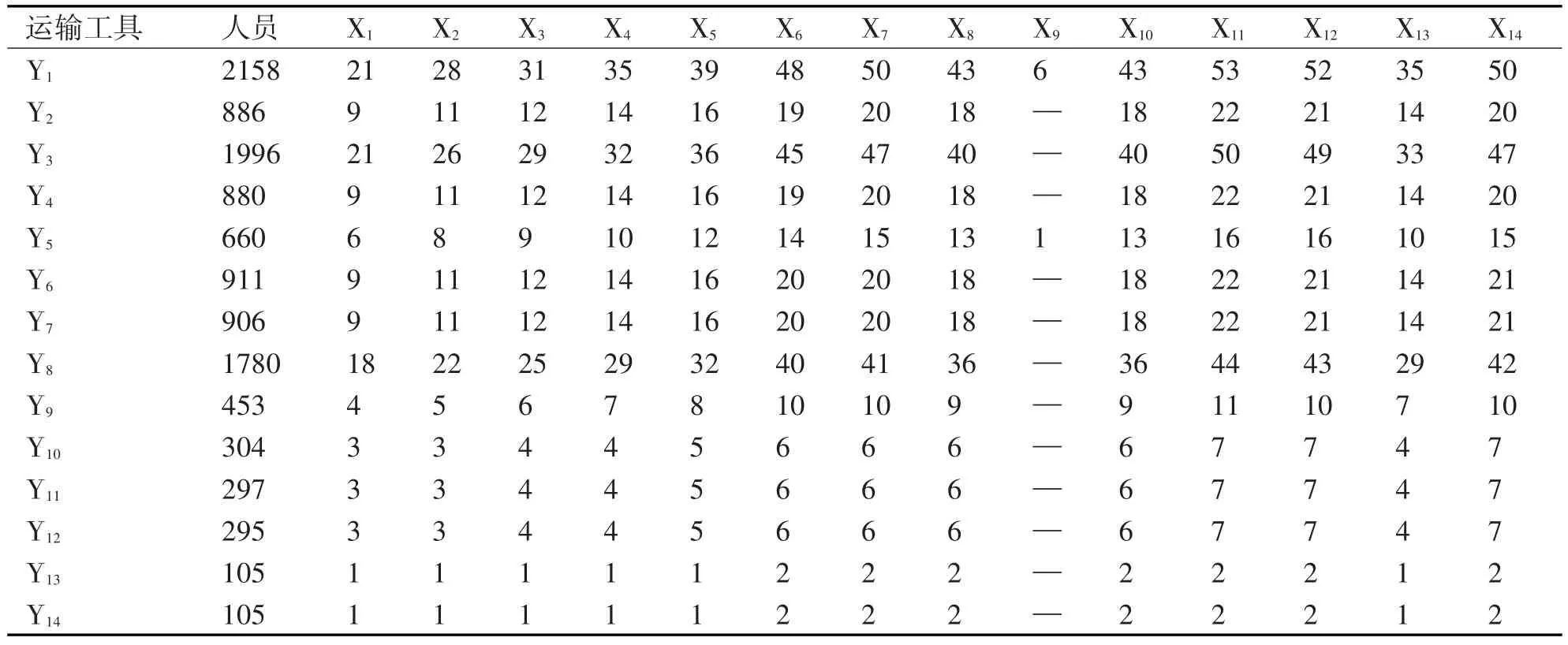
表2 各类型运输工具的装载能力

表1 I型旅的一个旅级单位的输送任务

4.2 具体求解步骤

按照模型运算的流程，将相关数据按照装备类型的优先级循环输入至程序中。循环计算使用每一种类型的运载工具进行转载某种类型装备的“装载完成率”。判断Ni是否小于i型装备的原有数量，如果“否”，则直接删除接删除运载工具i装载装备j的方案［12］。其可能的可行方案的装载完成率的计算结果如表3所示。而后再进行多次循环，求出I型旅大部分装备的装载方案如表4所示。

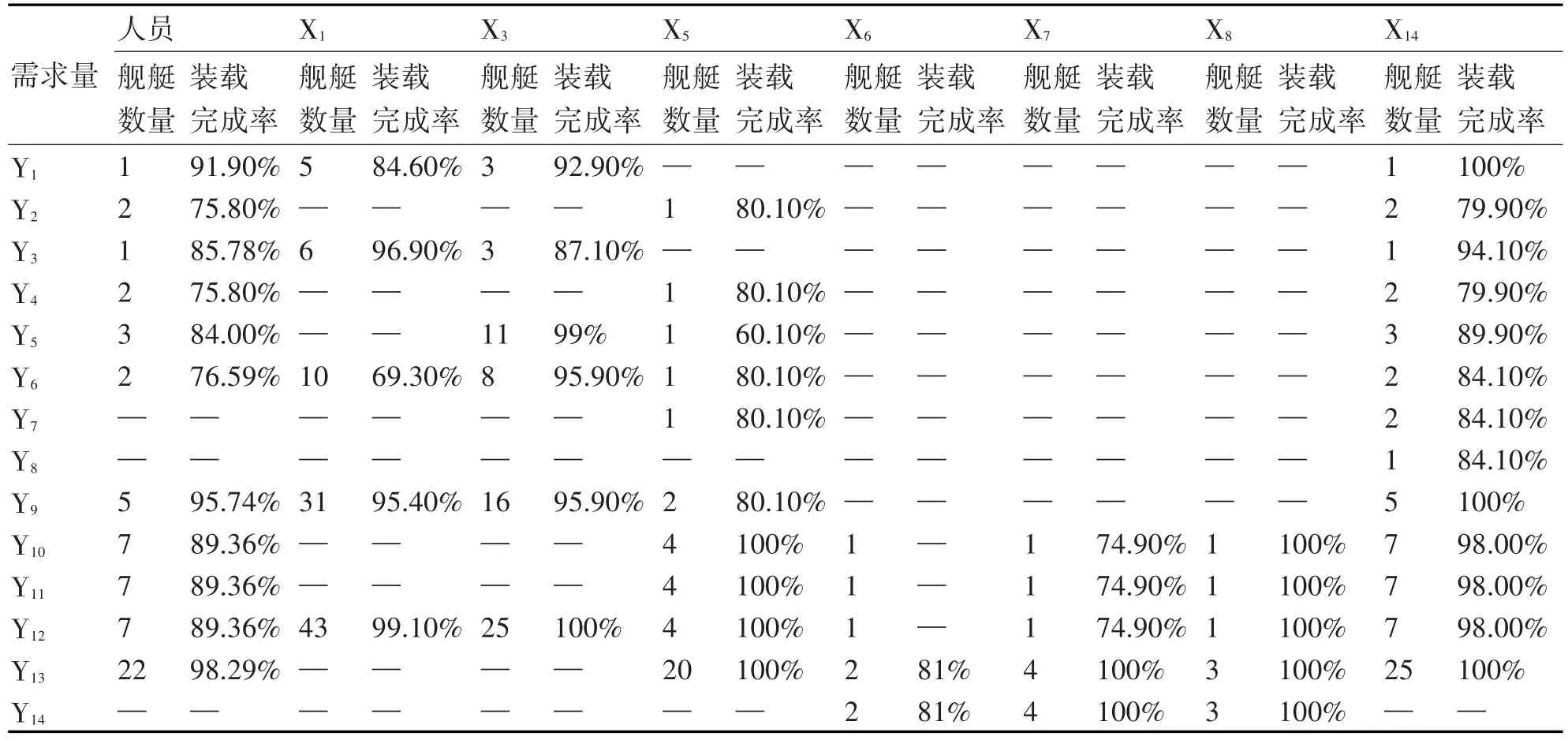
表3 可行方案的装载完成率

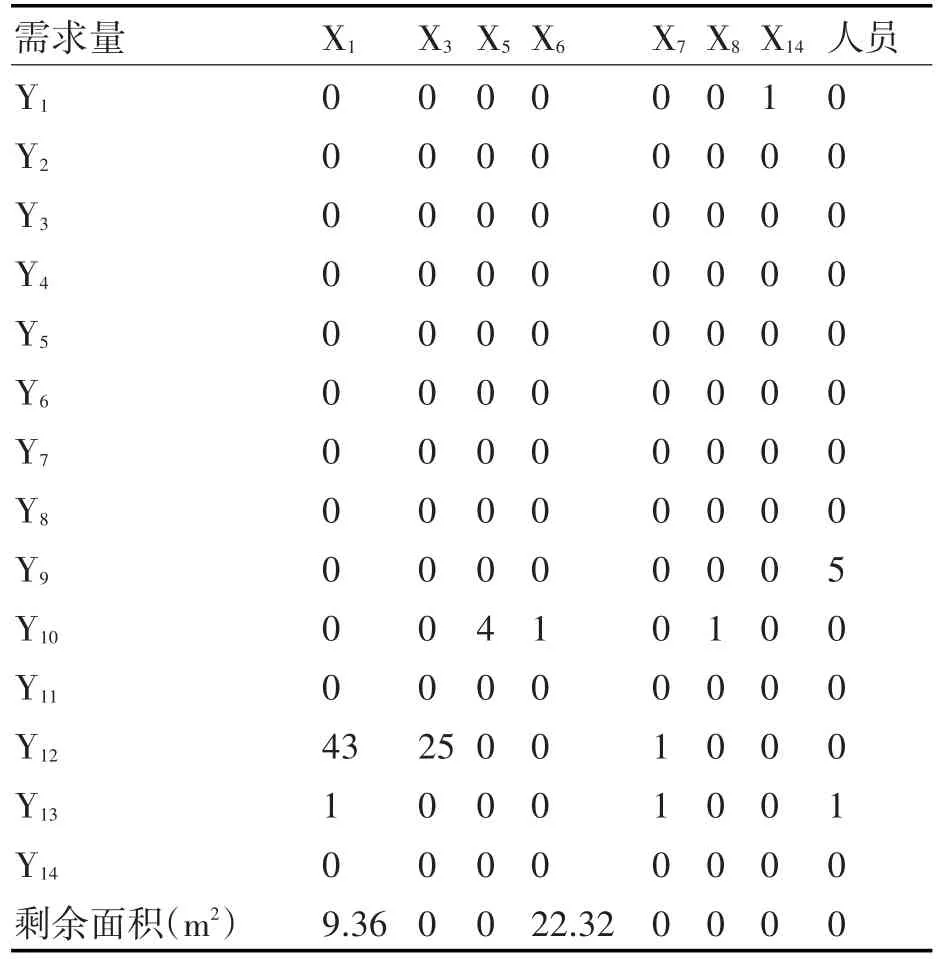
表4 I型旅装备的初步装载方案

以上结果即求得了单一类型装载原则下的部分装载方案，通过运用遗传算法和启发策略，结合Matlab编程工具，对“装备余料”的装载进行求解。即可求出I型旅所有装备的装载方案如表5。

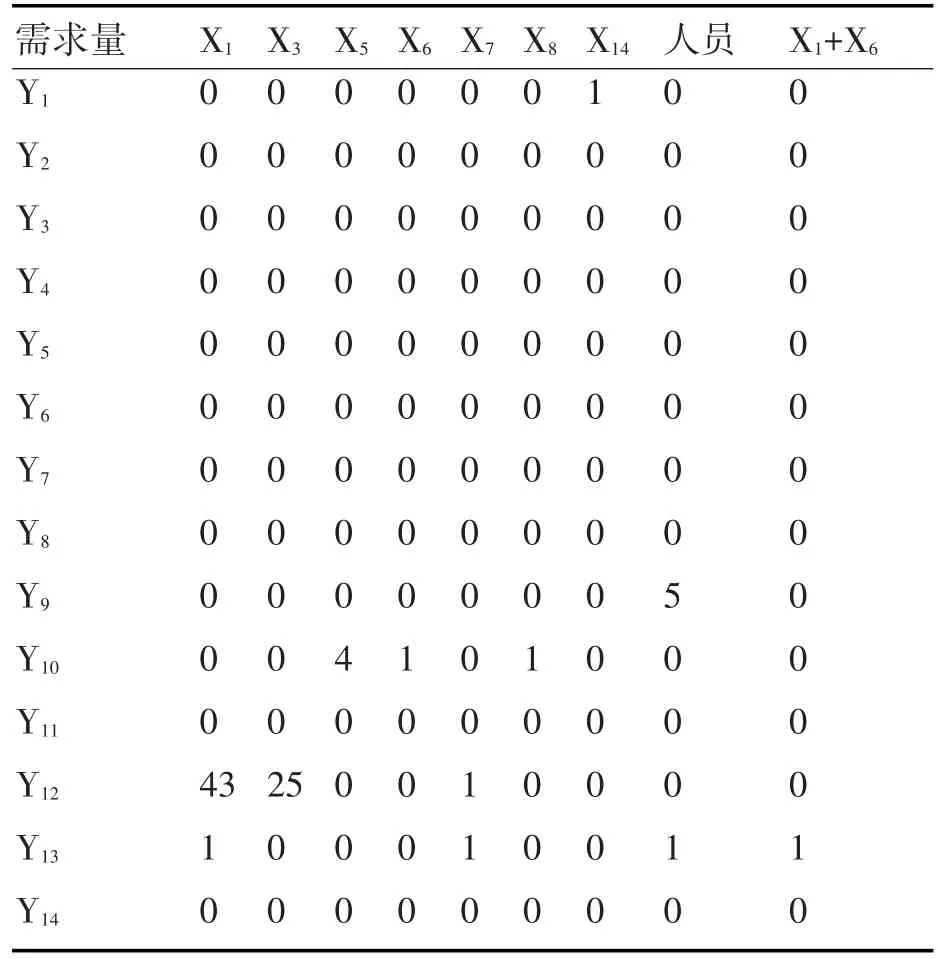
表5 I型旅所有装备的装载方案

上述表格即代表了I型旅的装载方案，表格的纵坐标表示运输工具的种类，横坐标表示单舰装载方案。例（Y12，X1）=43代表用43艘Y12运输工具以只装载 X1装备的方案装载，（Y13，X1+X6）=1代表用1艘Y13运输工具以混合装载X1装备和装备X6的方案装载。其中，“0”代表未使用该类型船。

4.3 求解结果分析及评价

正如前文评价方案制定所述，对上述方案进行评价，通过计算各个运载工具上的实际装载重量与最大载重限制相比较，即可判断上述方案是否可行。经计算比较，上述方案均未达到最大载重限制。另外，上述方案可能并不是实际情况中I型旅级单位装载方案的唯一解和最优解，但是基于本文提出的优先单一类型装载的原则，上述方案从理论上讲确实是最优解，这对有效提升部队跨区训练的装载效益，具有重要意义。

5 结语

本文针对部队跨区训练海上运输中存在的工具选择不恰当、装载方案不合理等问题，通过运用Matlab辅助工具，设定优先级原则，以“装载完成率”和“利润”最大化为目标函数，建立了基本的数学模型，探索出适合求解的“多次循环多次判断装载法”，并结合I型旅的装载任务进行了运用和评价。针对装备、物资的装载，提供了行之有效的方法，进而获得最佳的运载方案。