RAIN:一种面向软硬件和门限实现的轻量分组密码算法
2021-06-04曹梅春张文英陈彦琴邢朝辉
曹梅春 张文英 陈彦琴 邢朝辉,3 吴 磊
1(山东师范大学信息科学与工程学院 济南 250358) 2(三未信安科技股份有限公司 济南 250014) 3(山东交通学院理学院 济南 250357)
分组密码算法作为对称密码的一个重要分支,在计算机通信和信息系统安全领域有着广泛应用,同时也是构造认证加密算法、Hash函数和密码协议的底层算法.分组密码的典型结构主要包括Feistel结构、SPN(substitution permutation network)结构和Lai-Massey结构.Feistel结构代表有数据加密标准(data encryption standard, DES)算法[1]和NSA(National Security Agency)设计的SIMON算法[2]等;SPN结构的算法有高级加密标准(advanced encryption standard, AES)[3]、轻量级分组密码算法Midori[4]和SKINNY[5]等;Lai-Massey结构的算法有国际数据加密算法IDEA[6].Feistel结构加解密采用相同的结构,加解密算法同时实现可以节省资源,但是由于其混淆扩散速度慢,一般轮数比较多,加解密效率相对低一些.而Lai-Massey结构的混淆扩散速度较快,加解密一致,且软件实现速度快.但是轮函数较为复杂,每轮的硬件实现面积较大.SPN结构混淆扩散速度快,算法轮数一般较少,算法实现时吞吐量较大.一般情况下加密和解密的部件是不同的,解密是加密运算的逆.一些SPN结构加密算法实现解密的开销通过使用对合运算作为组成部分来进行优化.在SPN结构中,有一类是基于S盒和乘矩阵的AES类结构,该类结构算法有利于对抗差分和线性分析,并进行安全性证明.
轻量级分组密码是一种特殊的分组密码体制,对轻量级分组密码进行研究的动机是某些特定应用需要比AES面积低、功耗低且安全强度相当的加密算法.轻量级密码算法硬件实现和运行时所占用的系统资源的开销较少,例如硬件实现面积、运行时所占内存空间大小和能耗等.这类分组密码算法主要被用于资源受限的计算环境中,例如电子标签射频识别(radio frequency identification, RFID)以及一些电池驱动的设备.随着物联网的快速发展,物联网终端传感器部件广泛部署,对轻量级密码体制的需求也越来越大[7].由于轻量级分组密码具有较低的实现成本和较低的能耗,在物联网终端和卫星通信网络中大量部署轻量级密码算法可以带来显著的社会经济效益.第1代轻量级密码,例如PRESENT[8]和KATAN[9]仅关注芯片面积,并使用非常简单的轮函数作为算法的主要组成部分.近年来,具有各类特色的新轻量分组密码如雨后春笋般涌现.例如短代码型PRIDE[10]和SPECK[2],低延迟型PRINCE[11],MANTIS[5],QARMA[12],能抵抗侧信道攻击型LS-Designs[13]和PICARO[14],以及低能耗型Midori和GIFT[15].
小型加密设备适用于物联网中,轻量级加密算法的侧信道保护实现是一个非常重要的方面,防止侧信道攻击的一种额外保护措施是使用防泄漏设计,尤其是通过对密码进行额外的调柄(Tweak)输入.轻量级可调分组密码通过附加的公开输入Tweak进行扩展.这样的算法允许更好的加密模式和认证加密方案的有效构造[16].这类算法包括SKINNY[5],CRAFT[17],Deoxys-BC[18],QARMA[12],Joltik[19],以及作为一般设计原则的TWEAKEY框架[20].
安全是密码算法得以应用的前提.近年来,分组密码的安全性评估己取得长足的进步.特别是,基于混合整数线性规划(mixed integer linear programming, MILP)方法的提出和应用[21-23],使得分组密码算法安全分析朝着自动化、精细化、标准化、可证明方向发展.
1 RAIN分组密码
RAIN是一族可调分组密码算法,分组长度支持64 b和128 b,根据分组长度的不同记为RAIN-64和RAIN-128.两个版本调柄的长度等于密钥长度分别为64 b和128 b,它们的迭代轮数分别为30轮和36轮.
1.1 符号说明
符号说明如表1所示:

Table 1 Symbols and Descriptions表1 所用符号及说明
1.2 RAIN算法描述
算法的轮函数由4种运算组成:列混合、字替换、行移位和轮可调密钥加.图1和图2分别展示了RAIN算法的轮函数结构和算法的整体结构.令n比特向量(w0,w1,…,wn-2,wn-1)表示一个密码内部状态ST,最左比特w0代表最高有效位,若将内部状态从左至右每n/16比特划分为一个单元,则密码内部状态ST可表示为(st0,st1,…,st15),其矩阵形式为
其中,st0表示内部状态的最左单元,st15表示内部状态最右单元,每个单元st中最左比特代表最高有效位.
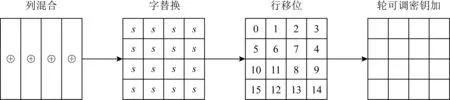
Fig. 1 The round function of theRAIN algorithm图1 RAIN算法的轮函数结构

Fig. 2 The overall structure of the RAIN algorithm图2 RAIN算法的整体结构
RAIN算法的具体加密流程:
1) 初始白化(Whitening).将明文P与密钥K按单元进行异或运算.
2) 列混合(MixColumns, MC).密码内部状态矩阵的每一列乘以下二元矩阵:
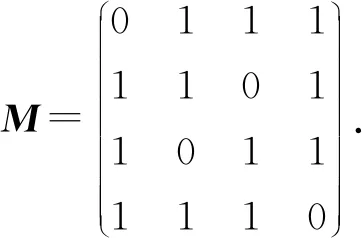
3) 字节替换(SubCells, SC).将s×s的S盒并行应用于密码内部状态的每个单元,当分组长度为64 b时s=4,当分组长度为128 b时s=8.表2给出了RAIN算法所用S盒S4的十六进制表示形式:

Table 2 The Truth Table of RAIN S -box S4表2 S盒S4的真值表
当s=8时所用8 b的S盒S8是经过与SKINNY所用8 b的S盒相似的变换而来,即通过并行放置2个4 b的S盒S4来构造如图3所示8 b的S盒S8.

Fig. 3 The 8 b S -box S8图3 8 b的S盒S8
4) 行移位(ShiftRow, SR).采用与AES相同的行移位变换,密码状态的第2~4行分别向左循环移动1,2,3个单元.
5) 轮可调密钥加(AddTweakey, ATK).将轮可调密钥RTKi与步骤4)的输出进行异或运算.
轮可调密钥编排流程:
① 密钥加(AddKey, AK).令轮可调密钥经过密钥加之后的状态为TAK,则首轮可调密钥更新中密钥加计算记为TAK=T⨁K.随后的第i轮中TAK=RTKi-1⨁K,2≤i≤30或36.
② 行移位(SR).对密钥加(AK)运算的输出状态使用与轮函数相同的位置变换.
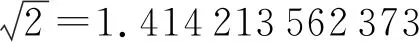

Table 3 The Round Constant RC of RAIN-64表3 RAIN-64版本的轮常数RC
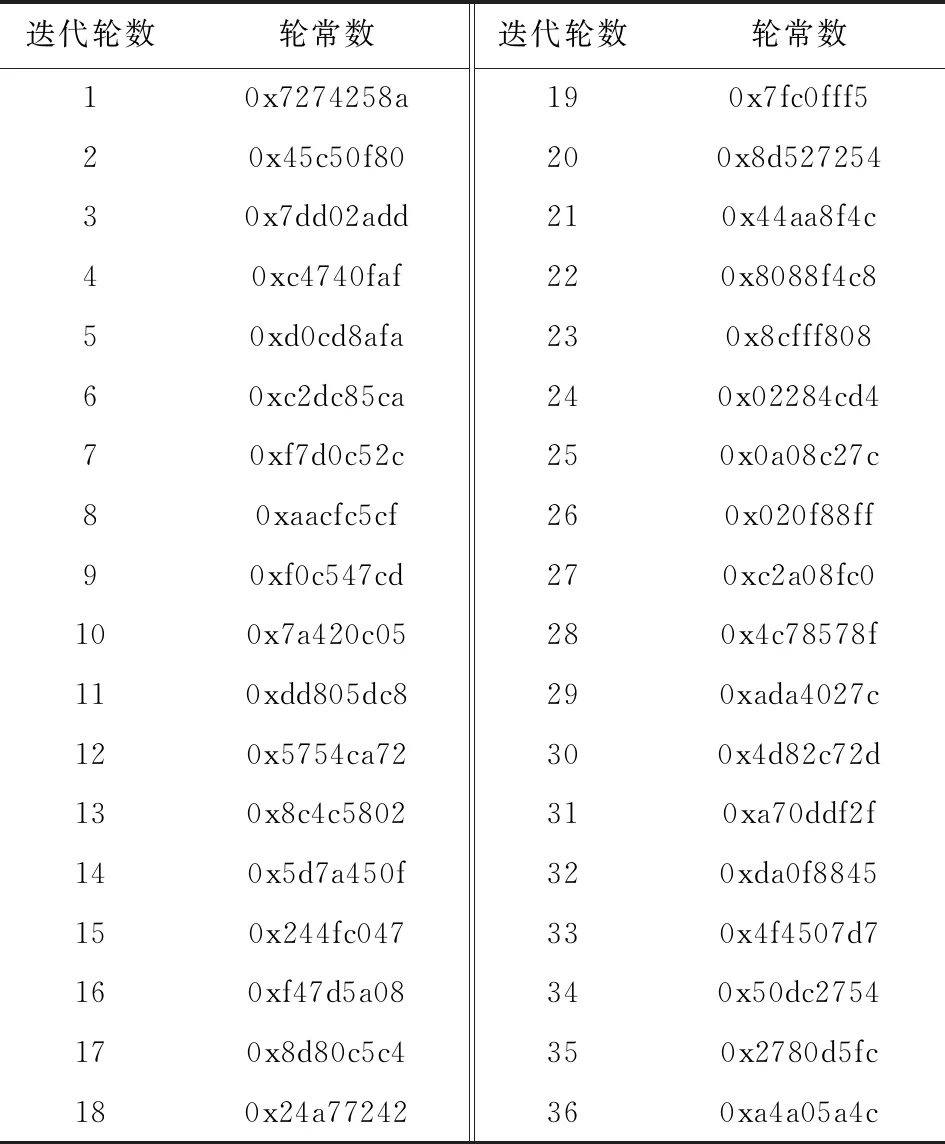
Table 4 The RoundConstant of RAIN-128表4 RAIN-128版本的轮常数
④ 比特加(AddBit, AB).令轮可调密钥编排过程中轮常数加运算的输出状态为TAC,则比特加运算可描述为:提取状态TAC中每个单元的第1比特,将提取的16个比特进行异或运算得到1 b的输出,即:
TAC[0][0]+TAC[1][0]+…+TAC[15][0],
运算结果用于替代状态TAC中每个单元的第1位即为比特加运算的输出RTK.
加密过程和解密过程伪代码见算法1和算法2所示.实现RAIN算法的代码可通过https://github.com/CaoMeichun/RAIN.git获取.RAIN算法的测试向量见附录A.
算法1.加密算法.
输入:P,K,T;
输出:C.
①stateWhitening=P⨁K;
② for 1≤i≤Nrdo
③stateMC=M·stateWhitening;
④ for 0≤j≤15 do
⑤stateSC[j]=Ss(stateMC[j]),s=4,8;
⑥ end for
⑦ for 1≤j≤15 do
⑧stateSR[j]=SR(stateSC[j]);
⑨ end for
⑩stateATK=stateSR⨁RTKi;
算法2.解密算法.
输入:C,K,T;
输出:P.
①stateMC_inv←C;
② forNr≥i≥1 do
③stateRTK_inv=stateMC_inv⨁RTKi;
④ for 0≤j≤15 do
⑤stateSR_inv[j]=SR-1(stateMC_inv[j]);
⑥ end for
⑦ for 1≤j≤15 do
⑧stateSC_inv[j]=Ss-1(stateSR_inv[j]),s=4或8;
⑨ end for
⑩stateMC_inv=M·stateSC_inv;
2 算法轮函数的设计
我们的设计遵循强安全性、高效的软硬件实现、简单的结构以及强灵活性等宗旨.RAIN的整体结构为SPN结构,S盒的选择是密码设计中的关键,对于4 b的S盒,我们将S盒的差分均匀度设为4,并将线性度设为8.当2个条件都满足时,我们筛选出具有安全性的S盒.扩散层的设计既要为算法获取良好的安全边界也要考虑到软硬件实现的性能,另一个重要标准是使得加密过程中密钥尽可能快地影响密码内部状态.轮常数的选取需遵循3个原则:1)区分不同的轮并避免对称性;2)使子空间密码分析复杂化;3)避免利用S盒中的固定点进行攻击.
2.1 RAIN算法的S盒设计
本算法采用4×4安全轻量S盒以及基于此S盒构造的8 b输入输出S盒.S盒的选择不仅考虑了如差分密码分析和线性密码分析等常规的安全性,还考虑了S盒的门限实现方案以达到抵御侧信道攻击的目的.
RAIN算法2个版本均采用4 b的S盒,一个原因是4 b的S盒可以用单指令多数据流扩展(streaming SIMD extensions, SSE)等指令集快速实现,另一个原因是硬件实现代价的考虑.和8 b的S盒相比,4 b的S盒具有明显的硬件优势,不仅硬件实现代价小,而且延迟能耗等方面都有明显优势.采用由2个并行处理的4 b的S盒组成8 b的S盒,以最小化基于轮的实现中的路径延时.该结构采用4 b的S盒构造非线性变换层,相较于AES等算法采用的8 b的S盒,更易于硬件实现,延迟、面积、能耗等指标更优.其次,4 b的S盒在各种平台的软件实现灵活,可以采用查表方式,也可以采用比特切片的实现方式.

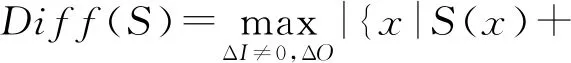
(1)
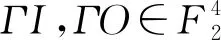
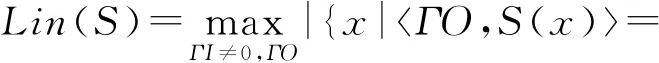
(2)
其中s的值为4.
对于任意双射4 b的S盒,均有Diff(S)≥4且Lin(S)≥8,当这2个值都达到最小时,可以称该S盒为最优S盒.
RAIN算法使用的S盒的差分均匀度、非线性度以及线性度为别为4,4,8,该S盒的密码学性质达到了最优.且此S盒代数次数为3,同时兼顾了S盒高代数次数的要求.
2.2 S盒的门限实现
S盒门限实现[26-28]为加密算法的实现提供了可证明的安全性,用来抵抗侧信道攻击.本文S盒S4的布尔表达式为
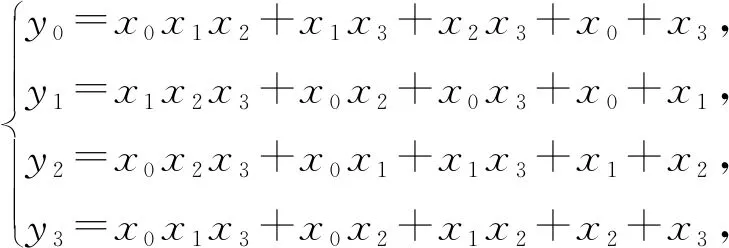
(3)
其中,(x0,x1,x2,x3)表示S4的4 b输入变量,(y0,y1,y2,y3)表示S4的4 b输出变量.S4的1个分量函数y0由1个立方项、2个二次项和2个一次项组成.为了降低硬件实现中的电路复杂性以及缩减电路开销,将代数次数为3的分量函数转换为代数次数为2的子函数的复合,然后对这些子函数进行门限实现.共享份额[29]为3的门限实现方案[30]见附录B.
此门限方案中,秘密信息被随机地分成了多个份额,即使其中某个份额的信息被泄露,也不会对此S盒造成威胁.
由于S4其余的3个分量函数可通过该分量函数y0中变量的循环移位获得,其余的3个分量函数的门限实现方案与y0相同.在进行硬件实现时,它们的面积开销与功耗也相似.
2.3 RAIN算法的扩散层设计
扩散层的设计是为了提供扩散,因此输出的每一列依赖于输入的某些列.在算法的扩散层结构上,我们希望扩散层便于解密过程的求逆,并且解密逆运算和加密正运算的性能是等价的.同时还考虑了扩散层和S盒产生强扩散的计算资源和实现效率,要求每个比特使用的异或数量不能超过3个.考虑到可逆性,我们利用对合矩阵M构造扩散层,使线性层的加密和解密可以使用相同的代码块来减少算法实现所需指令的数量.
分支数反映了线性扩散层的安全性能,扩散层的分支数越大,在进行差分密码分析或者线性密码分析时需要选择(己知)明文数越多,密码的安全性就越好.分组密码的扩散层都可以表示为有限域上的线性变换操作,所以设计一种高扩散性的密码算法就相当于设计一个具有最大分支数的线性变换.

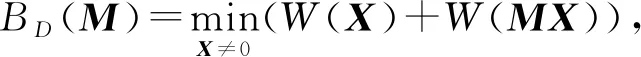
(4)
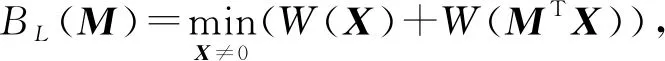
(5)
其中,MT是矩阵M的转置,W(X)表示向量X的汉明重量.
定义3.若一个m阶矩阵的差分分支数和线性分支数均等于此矩阵的阶数m,即BD(M)=BL(M)=m,则该矩阵M是几乎最优极大距离可分码(maximum distance separable, MDS)矩阵.
虽然许多加密算法使用MDS矩阵作为扩散层,但不可否认的是,MDS矩阵在提供了最优的扩散性能的同时,使算法效率下降,这将消耗更多的软硬件资源,算法的实现需要更长的运行时间.我们使用线性分支数和差分分支数均等于4的几乎最优MDS矩阵,从而在安全性和效率之间取得最佳平衡.几乎最优MDS矩阵都具有次优的分支数,但是与MDS矩阵相比,它们的实现代价小,具有更高的硬件和软件实现效率.几乎最优MDS矩阵只需要简单的异或运算,从而大大减少了硬件和软件资源的消耗.
3 安全性分析
3.1 差分分析
差分分析是最初由Biham和Shamir[31]于1991年针对DES算法提出的一种密码分析方法.该方法几乎适用于所有的分组密码体制,是对分组密码算法威胁最大的分析方法之一[32-33].对于采用S盒作为核心部件的分组密码算法,评估单条差分传播路径最大概率上界的最有效方法就是估算差分传播路径中活跃S盒的个数.2011年Mouha等人[21]利用混合整数线性规划给出差分分析和线性分析中活跃S盒个数下界的评估方法.首先将差分分析和线性分析中活跃S盒传播规律用线性不等式刻画,目标函数为最小的活跃S盒个数,然后利用求解MILP问题的软件进行求解,如Cplex,Gurobi等.该方法得到的下界精度较高,许多时候达到最优值,因此被广泛用来作为评估分组密码抵抗差分分析和线性分析能力的参考指标.

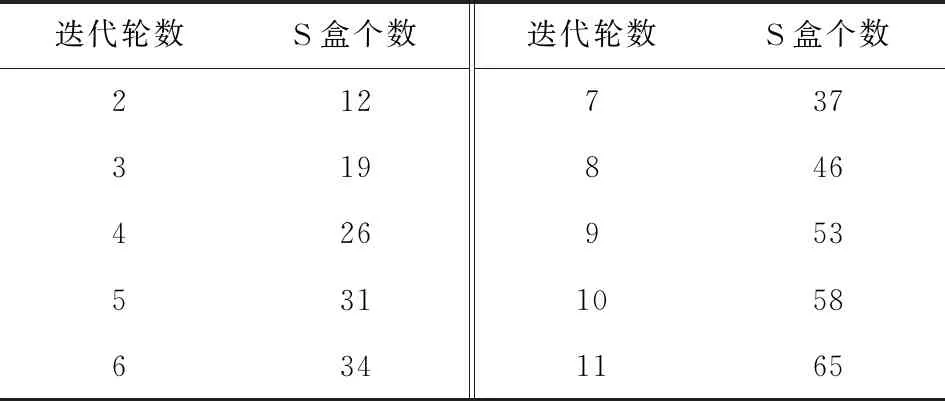
Table 5 The Minimum Number of Differential Active S -boxes Corresponding to the Different Number of Rounds表5 各迭代轮数对应的最少差分活跃S盒个数
我们将RAIN-64的最小活跃S盒与其他轻量级分组密码在相同安全级别64 b分组128 b密钥上进行比较,结果如表6所示(表6中所有加密都使用4 b的S盒,最大差分概率为2-2):

Table 6 Comparison of the Minimum Number of Differential Active S -box Corresponding to the Different Number of Rounds Between RAIN-64 and Several Algorithms表6 RAIN-64与若干算法各轮最少差分活跃S盒的比较
3.2 不可能差分分析
不可能差分分析是利用概率为0的差分路径进行密码分析的分析方法[34].根据不可能差分密码分析的研究现状,一个分组密码的最长不可能差分区分器的轮数接近于全扩散轮数的2倍.对于RAIN算法而言,当输入差分汉明重量为1时,4轮可达到差分全扩散.
我们利用基于MILP的自动化搜索方法对RAIN的不可能差分路径进行搜索.由己知的不可能差分分析结果来看,几乎所有的不可能差分路径的输入和输出差分模式分别只有一个活跃S盒,因此选定输入输出差分时,应满足输入、输出只能使单个S盒活跃.搜索到RAIN算法的6轮不可能差分形式为
*000 0000 0000 0000|→*000 0000 0000 0000.
利用不可能差分区分器,可以给出缩减轮RAIN的不可能差分分析.考虑到RAIN算法的扩散性和迭代轮数,可以相信全轮RAIN针对不可能差分分析提供了足够的安全冗余.
3.3 积分分析
积分分析可以看成是一种代数攻击,主要构造关于若干输入明文比特的零和区分器.可分性(division property)是目前分析对称密码算法积分性质最有力的工具[35-38],同样可以借助MILP方法方便准确的搜索算法的积分区分器.我们利用Xiang等人[36]以及Zhang等人[38]提出的生成S盒及线性层可分性不等式的方法构造了RAIN算法可分性传播的MILP模型.文献[36]中对S盒可分性传播的不等式描述近乎完美.文献[38]中利用线性层矩阵所描述的异或运算,通过构造线性不等式来建模可分性在线性扩散层中的传播,使不等式的可行解精确地表示线性层的所有可分性传播轨迹.因此,利用该方法描述是紧致的,得到的解是最优的,轮数是用可分性方法所得最多的.借助可分性可以搜索得到RAIN-64算法的7轮积分区分器,其中输入63个活跃比特,输出4个平衡比特.
7轮RAIN-64积分区分器的输入为
0111 1111 1111 1111…1111 1111 1111 111,
其中“1”表示活跃比特位;
7轮RAIN-64积分区分器的输出为
????BBBB????????…????????????????,
其中,“B”表示平衡比特,“?”表示未知状态.
受限于计算能力,目前还无法断定RAIN-64是否存在8轮积分区分器,但是我们构造出的积分区分器的轮数7和RAIN-64的总轮数30相差很大.因此我们相信RAIN-64具有足够的抵抗积分密码分析的安全性.
3.4 不变子空间分析
我们采用Guo等人[39]提出的不变子空间分析方法对算法S盒的不动点导致的弱密钥存在性进行了分析.观察算法的S盒发现有可能存在的弱密钥空间为:{0,5,a,f},{1,9},{2,3},{4,6}.
由此我们考察了算法各个部件的输入输出可能性.当明文、调柄和主密钥都从以上某一个空间中取值时,密钥编排中的密钥加,行移位都不会改变输出值的空间.例如明文、调柄和主密钥都从{0,5,a,f}中取值,那么密钥编排中密钥加和行移位的输出值仍在{0,5,a,f}这个空间中.比特加操作会使{0,5,a,f},{2,3},{4,6}这3个空间不成立,因为该操作会改变半字节的最高位.而算法所使用的轮常数使得密钥编排经过轮常数加之后不能保持上述4个空间中的任何一个.虽然轮函数的每一步操作都使得输入输出空间一致,但是每一轮的密钥都无法与明文保持在同一个空间中,所以以上4个可能的弱密钥空间是不存在的.
4 软硬件性能评估
4.1 软件性能评估
RAIN算法便于软件实现,算法可以采用基于字的基本逻辑运算实现.
RAIN算法使用的矩阵M每行有3个1,在计算输出状态矩阵列向量时,可以通过增加辅助变量t达到减少使用模加运算的目的.
令乘矩阵的输入为(x0,x1,x2,x3),输出为(y0,y1,y2,y3),输出向量可由输入向量计算得到:
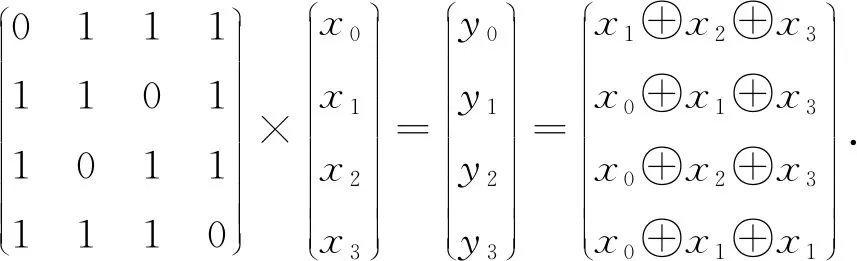
(6)
若引入辅助变量t=x0⨁x1⨁x2⨁x3,则输出向量可计算为
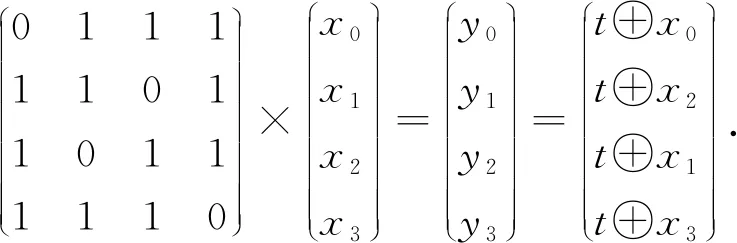
(7)
通过式(6)计算输出列向量所需模加数量为7个,而式(7)计算输出列向量所需模加数量为8个.
我们采用标准C实现RAIN算法,在64 b Windows(i7-7700 CPU@3.6 GHz;Win7操作系统;16 GB内存;x86_64环境;编译器为visual studio2017 x64 release)和64 b ARM(TaiShan 200 MHz CPU@2.6 GHz;Cortex A73架构;编译器gcc 9.1.0)环境下,对RAIN算法的加解密速率进行测试,测试结果如表7所示:
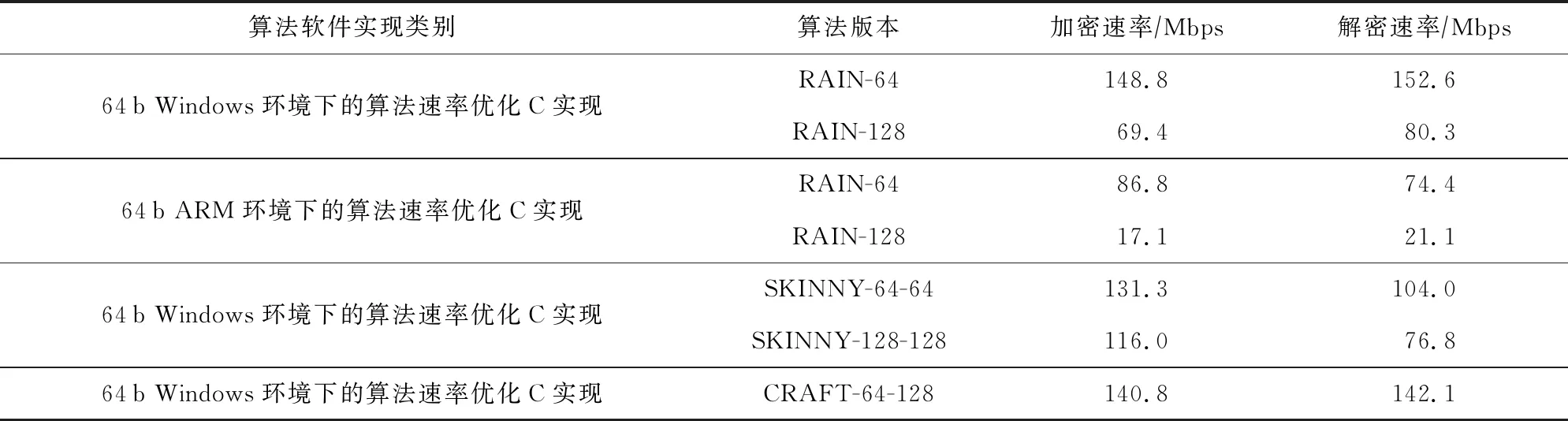
Table 7 Software Test Results of RAIN Algorithm表7 RAIN算法软件测试结果
表7中对RAIN算法的软件实现性能与其他提供相同安全级别的轻量级可调分组密码SKINNY和CRAFT进行了对比,RAIN-64算法的加解密速率是较高的.
4.2 硬件性能评估
为了评估RAIN的硬件实现性能,我们针对可编程逻辑阵列(FPGA)实现平台进行评估.使用Xilinx公司的Xilinx Kintex xc7k325tffg900-2平台来评估RAIN在FPGA上的实现结果和性能.算法实现的加/解密运算用时包含密钥编排运算用时.算法电路面积规模为包含加密、解密、密钥编排运算的算法整体实现的含互连线面积.表8给出了RAIN在FPGA上的实现结果,并将RAIN算法的实现与SKINNY进行了比较,RAIN算法的加解密速率更优且面积较小.

Table 8 Performance of RAIN in FPGA表8 RAIN算法在FPGA平台实现性能
5 结 论
本文设计了一个面向软硬件和门限实现的轻量分组密码算法,算法兼顾了安全性和软硬件实现性能.RAIN算法对64 b的分组和128 b的分组,采用统一的结构都可以转化为基于字的基本逻辑运算,这种实现方式在现代英特尔中央处理器架构下可以很方便地结合扩展指令SSE实现分组密码的并行处理,同时对S盒的门限实现方案在抗侧信道攻击上具有优势.
