高精度绝对式差极角位移传感器

张 辉，刘小康，彭 凯，蒲红吉，于治成，徐天慧

(1.成都玖锦科技有限公司，四川成都 610000；2.重庆理工大学，重庆 400054；3.重庆航天火箭电子技术有限公司，重庆 400039)

0 引言

随着自动化技术、精密测量技术的迅猛发展，数控机器人、航天火箭等行业对角位移传感器高精度、绝对定位的要求越加苛刻。例如在原子力显微镜的微探针角位移的检测中，要求其使用的传感器具有nm级别的角位移定位精度[1]。而对于大尺寸的精密测量对象(大型伺服电机元件)，在要求精确定位的同时还要求大量程，为此，国内外专家针对高精度绝对式角位移传感器技术开展了大量的研究工作[2-4]。

当前用于角位移测量的绝对式传感器主要有光栅、磁栅和容栅。绝对式光栅角位移传感器由于光波波长、光学衍射的制约以及栅线精密制造精度的限制，其精度难以进一步提高[5-7]。同时随着其刻线精密程度的增加，码元数量增加，绝对式光电编码器从光敏元件输出的码道信号增多，编码解码复杂，对绝对编码的发展造成了限制[8-10]。此外，基于光栅采用光学测量测得位移，工作环境中的粉尘污染、机械振动严重影响了其测量精度。德国HEIDENHAIN公司的绝对式光栅角位移传感器RCN8310在满足绝对式定位的条件下其系统精度可以达到±2″。日本TAMAGAVA公司的SA135系列绝对式角位移编码器在外径为135 mm时精度达到±4.5″[11-13]。

绝对式磁栅角位移传感器和绝对式容栅角位移传感器原理简单、成本低廉，具有较强的耐受性，粉尘污染、机械振动等对其影响较小。但磁栅由于其磁节距较大且抗电磁干扰性差，而容栅因其电容极片间的线性间隔由于杂散电容和条纹效应而非常有限，从而难以实现绝对式高精度测量或者有限测量范围内增量式测量精度高[14-16]。意大利GIVI公司的MR系列磁栅传感器在最大外径为72 mm时角位移分辨率达到25 μm(0.2″)。英国Renishaw公司的超微型磁栅RoLin传感器角位移分辨率可达0.24 μm(1.72″)，AksIMTM离轴绝对式磁旋转编码器精度达到±0.05°。安徽大学研究的圆容栅传感器在外径50 mm内，其测量误差不超过7 μm(0.08″)[17]。

基于上述问题，本文在前期研究基础上设计了基于交变电场的高精度绝对式差极角位移传感器。传感器利用单列式传感原理设计差极结构，采用外圈N对极进行高精度测量，利用内圈N-1对极与外圈整周相差一个周期的相位差实现绝对定位。对传感器整周均匀分布的电极施加4路正交激励信号形成交变电场，构建稳定的匀速运动参考系[18-19]。利用高频时钟插补计数实现高精度测量，降低对精密栅线制造的要求。同时传感器吸收了电容式传感器的优点，结构简单，无需复杂的编码解码，具有较强的高速抗干扰性，粉尘污染、机械振动等对其影响较小。传感器样机使用印制电路板工艺制造，降低传感器成本。

1 测量原理

1.1 角位移测量原理

差极角位移传感器原理如图1所示。角位移传感器结构如图1(a)所示，由转子和定子2部分组成。转子和定子都由内外两圈电极片组成，内圈形成N-1对极，外圈形成N对极,单圈结构形成单列式传感结构。转子以外圈为例，采用沿圆周均匀分布的2N个半正弦形极片作为感应电极，倘若将接出第一路输出的半正弦形极片作为第一片极片，那么沿着顺时针方向的第一片、第三片、第五片、…、整周最后一片第奇数(2N-1)片相连，形成P1路输入；沿着顺时针方向的第二片、第四片、第六片、…、整周最后一片第偶数(2N)片相连，形成P2路输出；P1、P2路输出形成差极输出，2N、2N-1两相邻电极极片形成一对极，整周形成N对极。定子以外圈为例，采用沿圆周均匀分布的4N个扇环形电极作为激励电极，倘若将接入第一路激励输入的扇环形极片作为第一片极片，那么沿着顺时针方向的第一片、第五片、第九片、…、整周最后一片(第4N-3片)极片相连，形成S+路输入；沿着顺时针方向的第二片、第六片、第十片、…、整周最后一片(第4N-2片)相连，形成C+路输入；沿着顺时针方向的第三片、第七片、第十一片、…、整周最后一片(第4N-1片)极片相连，形成S-路输入；沿着顺时针方向的第四片、第八片、第十二片、…、整周最后一片(第4N片)极片相连，形成C-路输入；S+、C+、S-、C-路4路输入形成正交输入，4N-3、4N-2、4N-1、4N相邻4片电极极片形成一对极，整周形成N对极。对S+、C+、S-、C-路4路激励电极依次施加如下4路频率(ω)相等，幅值为Am的激励信号US+=Amsin(ωt)、UC+=Amcos(ωt)、US-=-Amsin(ωt)、UC-=-Amcos(ωt)，形成2路差极感应输出(P1、P2路)，如图1(b)所示。

为便于理解，以外圈P1路为例分析角位移测量原理。S+路与S-路形成电容C1、C2，C+路与C-路形成电容C3、C4，电容间隙为d0，如图1(e)所示，从而C1、C2、C3、C4形成由2个差动电容电桥叠加而成的电路，其等效电路图如图1(d)所示。

根据电路叠加定理，可得其输出信号为

(1)

当转子相对定子发生位移时，假设C1、C2、C3、C4正对面积变化量为ΔSS+、ΔSS-、ΔSC+、ΔSC-，则感应输出为

(2)

当正弦形电极在正负扇环形电极上运动时，等效于扇环形电极在正负正弦形电极上运动，后者可视为余弦函数或正弦函数的不确定极限积分。当感应电极的旋转角度为θ时，激励电极与感应电极间的变化面积为S0，从正弦形极片到原点的半径是r，一片电极旋转角度的一半为45°/N，因此，4路正交信号的有效面积变化ΔSS+、ΔSS-、ΔSC+、ΔSC-为：

图1 差极角位移传感器原理

(3)

当感应电极运动经过对极内的4个激励极片时，依次得到4路感应信号，每路的感应信号受电极重叠面积变化与最大重叠面积比例的调制。因此，经4路信号调制的行波输出信号UO为

(4)

当P1、P2路同时工作时，2路感应输出信号Uouter1、Uouter2相位相反，经差分电路处理后得到输出行波信号Uouter为

Uouter=Uouter1-Uouter2=Asin[(nπ/180)+ωt]

(5)

式中A=2AmKe。

1.2 绝对位移测量实现原理

由于电极的重复周期性结构，使得传感器单圈结构的位移测量在整周测量过程中呈增量式增加，其误差也随位移增加而不断累积，因而不能准确定位传感器绝对位置。而传感器采用两圈差极结构，由于内圈、外圈传感信号的相位差在整周测量过程中呈线性增加，直至相差一个周期为止，因而能够确定传感器绝对位置。

设外圈和内圈对极数分别为N和N-1对极，router、rinner分别为内外圈的半径，内外两圈行波输出信号Uouter、Uinner分别为

(6)

式中：Aouter、Ainner分别为内、外圈信号的幅值;θouter、θinner分别为内、外圈的旋转角度。

在转子相对定子转动时，外圈N对极和内圈N-1对极分别构成两个匀速运动的运动参考系，采用信号US+作为参考信号Uref，内外圈的旋转角度如下：

(7)

式中：Mouter、Minner分别为外圈和内圈已转对极数；Pouter、Pinner分别表示Uref与外圈行波信号Uouter相位差脉冲计数值和Uref与内圈行波信号Uinner相位差脉冲计数值。

由于外圈和内圈所转过的角度相等，即θouter=θinner，而外圈与内圈所转过的对极数分2种情况：Mouter=Minner=M，Mouter=M=Minner+1，因而结合式(6)，内外圈相位差ΔP为

(8)

由此得到所走对极数M为

(9)

根据式(6)，计算得出含有绝对位置的角位移θ：

(10)

以外圈6个对极、内圈5个对极为例，如图2所示。当转子相对定子绕中心轴转动时，内外两圈信号在整个周期内刚好相差1个周期，见图2(a)，且2路信号的相位差在整个周期内具有唯一性，见图2(b)，能够实现绝对角位移测量。当忽略整周运动中由于仿真时跨对极所造成的相位差下掉现象，2路信号实际相位差呈线性增加，见图2(c)。

(a)

(b)

(c)图2 差极原理

1.3 传感器信号处理系统

传感器信号处理系统如图1(c)所示。当定子与转子发生相对运动时，内外圈传感结构分别输出正弦形行波信号Uinner、Uouter，与参考信号Uref通过前置电路放大、滤波、整形后，输出同频的方波信号。将3路方波输入FPGA信号处理系统，利用高频时钟信号进行插补计数，如图1(e)所示。将Uouter与Uref、Uouter与Uinner进行比相，利用高频时钟脉冲Pc对其进行插补，得到外圈信号相位差Pouter的时钟插补脉冲数m，2路信号相位差ΔP的时钟脉冲计数值n。因此根据式(8)，可计算出角位移值θ：

(11)

2 传感器性能测试

2.1 实验平台的搭建

传感器外圈布置200对极、内圈为199对极，两圈径向间隙为2 mm，电极最小宽度和间隙均为0.2 mm，采用PCB多层工艺制造，具有低成本和易于电路集成的优势。传感器样机外径为154 mm、内径为100 mm、尺子厚度为2 mm。

为验证传感器性能，搭建如图3所示的精度测试实验平台，主要由A1206-A1206-000型精密气浮转台、信号处理系统、测量系统、传感器组成。转子被固定在气浮转台上，定子与转子正对平行安装，并保证转台、转子、定子三轴同心，安装间隙d0为1 mm。在实验过程中，转子随转台绕中心轴旋转，定子保持静止。传感输出信号通过信号处理系统进行采集和处理，并与转台内置的RON-905型光栅(精度为±0.4″)采集的数据比较，最终测得实验误差数据。

1—测量系统；2—RPI气浮转台；3—转子与定子；4—信号处理电路图3 实验系统

2.2 实验结果

设置整周采样点数50点、对极内采样点数22点，采集传感器样机位移测量数据。图4(a)和图4(b)分别是传感器整周(360°)测量误差曲线和频谱分析图，图4(c)和图4(d)分别为对极内(2°)测量误差曲线和对极内误差频谱分析图。由图4可以看出传感器整周误差峰峰值达到17″，对极内误差峰峰值达到8″。频谱分析显示整周误差主要为二次谐波误差，其峰峰值达到3″；对极内误差主要为四次谐波误差，其峰峰值达到3″。

(a)整周误差曲线

(b)整周误差频谱分析

(c)对极内误差

(d)对极内误差频谱分析

3 误差分析与优化改进

3.1 整周二次谐波误差分析

在转子相对定子转动过程中，若传感器存在一定的不圆度时(即传感尺为椭圆状)，假设转动到短半径处时误差较小，则转动到长半径处时误差较大，而在整周运动中会2次转至长半径处，因而若以短半径处为起点，则传感误差会产生由小变大、再由大变小的2次变化，即二次谐波误差。在安装过程中由于转子、定子、气浮转台三轴不同心，则等效于转子相对椭圆状的定子转动，同理传感误差会产生二次变化，最终形成二次谐波误差。

在调整安装过程中，以传感器在0°、90°、180°、270°位置时其输出信号之差值作为安装判定依据，例如当0°与90°、90°与180°、180°与270°、270°与0°的差值相差在1″以内时则认定安装符合要求并能够进行测量。通过反复多次调整安装测定，发现每次调整安装后，输出信号在0°、90°、180°、270°之间的差值始终相差较大，主要呈现为二次变化。为此，通过圆度仪测量传感器的圆整度，在整周内采集20点，测量结果如图5所示。由图5可知，当传感器存在一定的不圆度时，会引入二次谐波误差。

图5 传感器不圆度曲线

3.2 对极内四次谐波误差分析

在传感器实际设计中，极片宽度和极片间的缝隙具有相同的数量级。因此，对于S+、C+、S-、C-4路中的激励信号而言，尽管半正弦形感应极片与扇环形激励极片在重叠区域是呈正弦变化的，但还应考虑4路信号在耦合输出过程中由于极片间缝隙的存在而致使输出信号不呈正弦变化的情况。传感器转子相对定子匀速转动时，在极片与极片间的缝隙处，传感器的电势分布从极片到缝隙再到极片呈现为一个由大变小、再由小变大的渐变过程[20]。而在—个对极内感应极片刚好经过4个缝隙，从而在测量过程中表现为四次谐波误差。

为验证其正确性并检验出最佳缝宽比(缝隙宽度与极片宽度之比)，采用4套缝宽比不同但其他参数不变的传感器进行对比实验，测得对极内实验误差如图6所示，此处，缝宽比为1∶5的传感器极片间缝隙宽度为0.1 mm、极片宽度为0.5 mm；缝宽比为3∶5的传感器极片间缝隙宽度为0.3 mm、极片宽度为0.5 mm；缝宽比为1∶1的传感器极片间缝隙宽度为0.5 mm、极片宽度为0.5 mm；缝宽比为6:5的传感器极片间缝隙宽度为0.6 mm、极片宽度为0.5 mm。

(a)不同缝宽比对极内误差曲线

(b)不同缝宽比对极内误差频谱分析图6 不同缝宽比对极内误差分析

实验结果表明，极片宽度为0.5 mm时，极片间缝隙为0.1 mm的对极内误差峰峰值约为9″，四次谐波误差约为3″；极片间缝隙为0.3 mm的对极内误差峰峰值约为8″，四次谐波误差约为2.8″；极片间缝隙为0.5 mm的对极内误差峰峰值约为3.5″，四次谐波误差约为1.25″；极片间缝隙为0.6 mm的对极内误差约为5.5″，四次谐波误差约为1.25″。由此看出当传感器缝宽比约为1∶1时，其对极内四次谐波误差最小。

3.3 优化改进

为避免传感器不圆度的影响，加长传感器定尺极片、缩短传感器动尺极片；为减小四次谐波误差，设计缝宽比为1:1的传感器极片结构。优化后传感器局部示意图如图7所示。

图7 优化后传感器局部结构示意图

改进结构后，传感器的测得实验数据如图8所示，整周误差峰峰值达到了5″，见图8(a)，对极内误差峰峰值从优化前的8″降为3″，见图8(b)，且其频谱分析显示对极内四次谐波误差得到了有效的遏制，见图8(c)。

(a)整周误差曲线

(b)对极内误差曲线

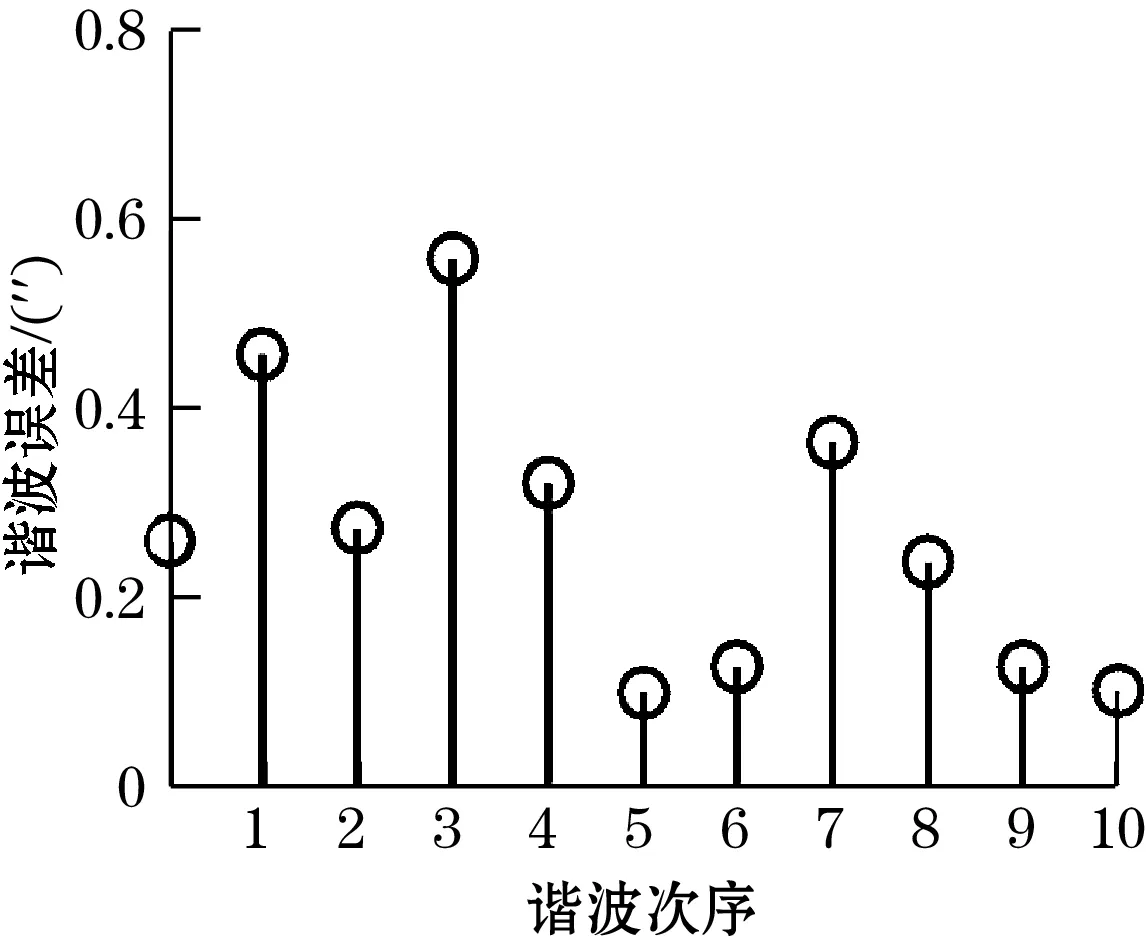
(c)对极内误差频谱分析图8 优化后传感器误差曲线

4 结论

本文在前期研究的基础上提出差极绝对式角位移传感器。传感器采用差极原理设计外圈200对极、内圈199对极，皆布置为单列式传感结构，保证了高精度测量；利用内、外两圈的相位差在整周范围内具有唯一性，实现了绝对定位。采用印刷电路板工艺制作外径为154 mm、内径100 mm的传感器样机。通过对样机性能进行实验分析，传感器整周存在较大的二次谐波误差，对极内存在较大的一次谐波误差。二次谐波误差来源于传感器的制造不圆度，四次谐波误差是由于传感器缝宽比的设计不合理。据此采用加长定尺极片、缩短动尺极片以消除由于安装、传感器制造等因素引起的二次谐波误差，并设计缝宽比为1∶1来减小四次谐波误差。优化后的传感器样机经实验验证表明，整周测量精度达到5″，对极内精度达到±1.5″。