非均匀海底环境下铰接超大型浮体的水弹性响应分析

夏彩波，位 巍，李 帅，付世晓

（1.上海交通大学a.海洋工程国家重点实验室，b.船舶海洋与建筑工程学院，上海200240；2.高新船舶与深海开发装备协同创新中心，上海200240）

0 引 言

超大型浮体（VLFS）被广泛应用于海上资源开发和军事基地的建立，具有重要的经济及军事战略意义。与常规海洋工程结构物相比，VLFS 尺度巨大且结构刚度相对较低，在波浪作用下的弹性变形不可忽略。因此，必须采用水弹性理论求解其在复杂海洋环境下的动力学响应[1-6]。

VLFS通常采用模块化建造，对于这种多模块连接而成的超大型浮体，在波浪作用下，各模块的运动不仅受到模块间的水动力干扰，还受到模块间连接件和结构弹性变形的约束作用。目前对于有连接件的VLFS 的研究方法主要有模态展开法和直接法。模态展开法即对特定的连接方式定义系统的模态，进而求解相应的水动力系数并建立整体系统的运动响应方程[7]。一些学者针对系统中连接件的个数[8]、模块以及连接件的刚度[9-10]、是否计入模块弹性变形的影响[11]等问题对结构响应的影响进行了分析，发现模块和连接件的刚度，以及模块的弹性变形对结构响应有重要的影响。模态展开法虽然可以减少计算量和存储量，但对于带连接件的复杂浮式结构物，不易准确地分析出系统的运动模态。因此，直接法被提出和采用，直接法认为n 个模块的系统存在6n 个自由度，根据连续特性补充位移连续条件，建立系统的整个运动方程[12-13]。这种方法虽然增加了计算量和存储量，但求解时可以考虑比较复杂的连接形式以及复杂的结构，具有普适性。

上述的研究均基于浮式结构物所处海洋环境是均匀的假定，而对于超大型浮体，其跨度较大（数千米），首尾两端所处的地理位置不同，波浪特征参数存在较大差异，波浪场的非均匀性十分明显。因此，对于VLFS 的结构设计有必要考虑非均匀海洋环境对浮体响应的影响。Song[14]采用有限水深格林函数的边界积分法和结构格林函数的平板理论，耦合求解了非均匀海底环境下的VLFS 的水弹性响应，并与试验工况进行了对比，证明了该理论的有效性。田超[15]基于缓坡方程和三维水动力学理论模型，开创性地提出一种工程简化计算方法，预报了岛礁附近浮式结构物在波浪中的运动与载荷响应，发现岛礁的存在对浮体运动响应的影响很大。上述学者预报了非均匀海底、岛礁环境下浮式结构物的动力响应，但对于非均匀海洋环境下带有连接件的VLFS的水弹性响应研究较少。

本文采用基于离散模块思想的水弹性分析方法[16]，对处于非均匀海底环境下的铰接超大型浮体水弹性响应进行了分析。首先，将VLFS离散为若干个模块，每个模块视作独立的刚体，然后应用三维势流理论并计及各刚体模块之间的水动力干扰，获得各个模块的波浪激励力、附加质量系数、阻尼系数及静水回复系数；其次，为保证结构位移的连续性，在各个模块重心点之间设置等截面和等刚度的伯努利-欧拉梁；然后，依据牛顿第二定律，将各个模块的水动力系数和弹性梁刚度阵进行耦合，得到连续浮体在波浪作用下的运动学方程；在此基础上，应用最小势能原理及拉格朗日乘子法得到铰接点处的约束矩阵、耦合约束阵和连续浮体运动学方程，建立铰接超大型浮体在非均匀海底环境下的运动方程；最后，在频域内求解该方程得到浮体的位移响应。通过梁的弯曲理论，得到在不同入射角度、波长和海底条件下超大型浮体的弯矩分布及铰接点处轴向力和垂向剪力。发现非均匀海底对铰接点的位移和受力有明显的影响，在超大型浮体设计中必须考虑非均匀海底的影响。

1 基本理论

基于多体动力学，将VLFS离散为若干个模块，每个模块视为独立的刚体，在水动力计算时考虑模块之间的水动力干扰。模块之间的位移连续性通过在模块重心之间设置等截面刚度的伯努利-欧拉梁来保证，从而建立基于多体动力学的VLFS的弹性响应分析方法。随后应用最小势能原理及拉格朗日乘子法得到铰接点处的约束矩阵、耦合约束阵和连续浮体运动学方程，建立铰接超大型浮体在非均匀海底环境下的运动方程。

1.1 坐标系的定义

本文首先基于离散模块思想，将连续的VLFS离散为由弹性梁连接的多浮体系统。为描述该多浮体系统在波浪作用下的水弹性响应，本文采用了三个右手坐标系，分别为大地坐标系OXYZ、参考坐标系o′mx′my′mz′m、随体坐标系omxmymzm（m = 1,2,...,N）。如图1 所示。其中，大地坐标系OXYZ 在空间固定，OXY 平面位于静水面，Z 轴竖直向上；参考坐标系o′mx′my′mz′m始终位于浮体的平衡位置，不随浮体摇荡；随体坐标系omxmymzm随各浮体一起运动，其初始位置与大地坐标系的坐标轴平行。规定波浪入射方向与X轴平行且指向X轴正向时，θ = 0°，逆时针方向为正。

图1 多浮体系统的坐标系Fig.1 Coordinate system of a multibody system

1.2 频域水弹性动力学方程

基于离散模块思想的频域水弹性方法[16]，将连续的VLFS 离散为由弹性梁连接的多刚体系统，然后应用三维势流理论获得各个刚体的水动力系数，将其与弹性梁刚度阵进行耦合，得到浮体在波浪作用下的运动学方程（如图2所示）为

式中：[M]、[A]分别为浮体总质量矩阵和附加质量矩阵；[C]、[c]分别为势流阻尼矩阵和结构阻尼矩阵；[K]、[k]分别为静水恢复力矩阵以及结构刚度矩阵；{ }u 为浮体节点处的位移矩阵；{ }F 为波浪激励力矩阵。

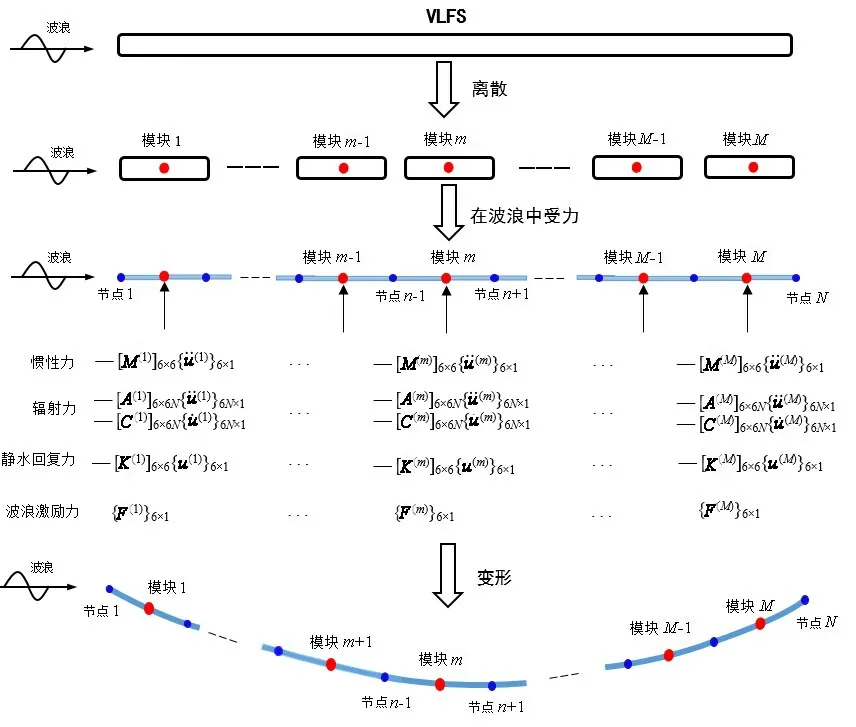
图2 频域水弹性方程建立过程Fig.2 Establishment process of frequency domain hydroelastic equation

1.3 铰接连接下浮体的水弹性动力学方程

当浮体之间有连接时，还需考虑连接件的影响。对于有连接的多浮体系统，频域水弹性方程可以改写为

式（2）可改写为

式中，[ L ]为约束矩阵，g为连接点处约束个数的总和。

对该方程取变分，得到

根据位能驻值原理δΠ = 0，可得

将式（8）整理为

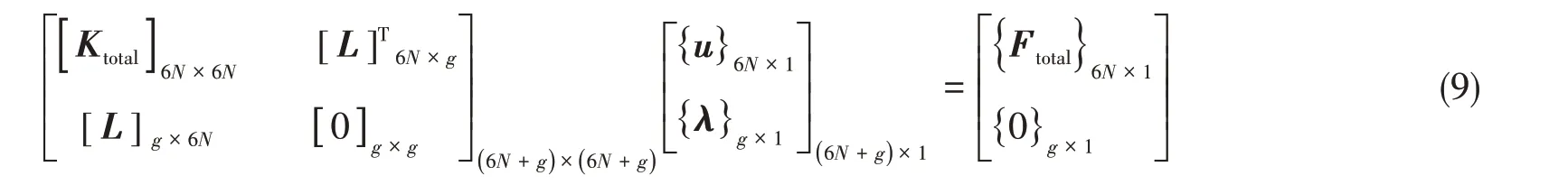
式（9）即为浮体间存在连接时的水弹性动力学方程。

当两个浮体模块铰接时（以结构仅可以绕y轴转动为例），约束矩阵[L]5×12的表达式[17-18]为

式中，(xi,yi,zi)是铰接点处的坐标，以上运算均相对于大地坐标系。

1.4 垂向弯矩及剪力

对于带铰的梁结构而言，分析其剪力和弯矩时，首先将梁从铰接点处分为两段，先求出铰接点处的剪力，再基于静力平衡求得任意断面的剪力和弯矩，具体求解过程见图3。

根据材料力学的知识，当梁上所有外力已知时，可用截面法计算梁的横截面上内力。取距o 端x处的任意断面s，以s 处左段梁为研究对象（见图3），作用在梁上的外力为各模块中心上的等效剪力和弯矩和，为满足左段梁的平衡条件，断面s 上存在内力SF 和BM，可以利用梁的弯曲理论得到。

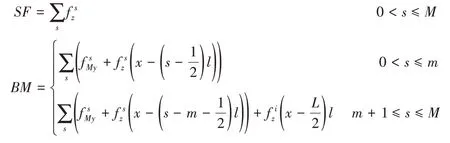
式中，l为单个模块的长度。

图3 带铰自由梁的静力平衡示意图Fig.3 Static balance of freedom beam with hinge point

2 模型介绍

2.1 VLFS体模型

模型参照Song[14]论文中的试验模型，即日本的Mega-Float[19]，PhaseⅡ。采用基于离散模块思想的水弹性分析方法[16]对VLFS 的动力响应进行求解，文中将VLFS 沿长度方向离散为20个子模块，如图4所示。VLFS以及子模块的参数见表1。

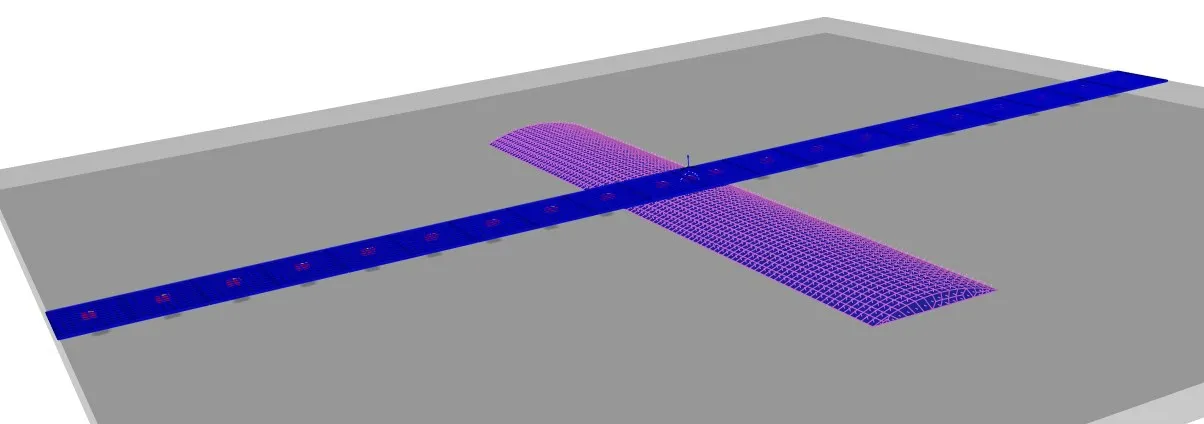
图4 非均匀海底环境下超大型浮体的数值模型Fig.4 Numerical model of VLFS under an uneven bottom

表1 超大型浮体与子模块的主要参数Tab.1 Main particulars of VLFS and substructures

2.2 非均匀海底模型

本文通过在海底设置二维沙丘来模拟非均匀海底。二维沙丘是一个截面为椭圆型的柱体，柱体长度是超大型浮体宽度的10倍，从而在该方向上可视为无限长，具体尺寸如表2所示，沙丘模型如图5所示。

表2 二维沙丘参数Tab.2 Dimensions of the shoal model

沙丘中心与浮体中心重合，长边与浮体长边垂直，具体的布置见图4。本文波浪入射波角度θ 为0°、30°和60°。由于参考文献中缺少连接件的位置和刚度信息，本文采用铰接形式，铰接点位于结构的中心，具体的布置见图6。

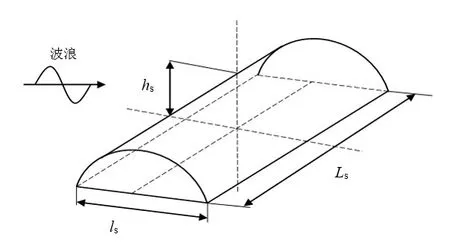
图5 二维沙丘模型Fig.5 Shoal model

图6 非均匀海底环境下超大型浮体的二维示意图Fig.6 Two-dimensional map of VLFS under an uneven bottom

3 计算结果及分析

3.1 垂向位移

图7和图8分别给出了两种结构模型（连续结构和铰接结构）在同一水深d=20 m，不同入射角度（θ=0°，30°，60°）和不同入射波长（λ=50，100，200，400 m）、不同海底分布下（Flat bottom and Bottom A）的垂向位移（wz/A）沿结构长度（x/L）方向的分布。其中，“Flat bottom”表示连续结构在均匀海底环境下的垂向位移；“Bottom A”表示连续结构在非均匀海底环境下的垂向位移；“Bottom A_hinged”表示铰接结构在非均匀海底环境下的垂向位移。从图7可以看出，对于同一波长情况下，随着波浪入射角度的增大，海底的非均匀效应逐渐变得明显，在结构垂向位移变化剧烈的同时对铰接点处的位移幅值影响也增大。

图7 不同波浪入射角下VLFS的垂向位移Fig.7 Vertical displacement of VLFS at different wave angles

图8 不同波长下VLFS的垂向位移Fig.8 Vertical displacement of VLFS at different wave lengths

从图8 中可以看出，随着入射波长的增大，海底的非均匀效应对结构垂向位移的影响逐渐增大，对铰接点处的幅值影响也逐渐增大，尤其以入射波长为200 m和400 m时较为明显。而在结构的首尾位置处，由于远离非均匀海底区域以及连接件位置，连续结构和铰接结构的垂向位移值大致相同。并且对于相同入射角度、入射波长以及海底情况下，铰接点的存在主要影响铰接点附近的垂向位移。

3.2 垂向弯矩

结构的受力情况是设计中所关心的问题，本文给出连续结构和铰接结构分别在均匀海底和非均匀海底下的垂向弯矩沿结构长度方向的分布，见图9和图10。从两图中可以看出，对于同一种结构形式，非均匀海底对结构垂向弯矩的影响与垂向位移相似，也是随着入射波长和入射角的增大，其非均匀影响逐渐增大。靠近结构首尾的位置，垂向弯矩在不同海底和不同连接形式下基本相同，这是因为波浪初始入射的位置远离海底非均匀的区域和铰接点的位置，因此不受非均匀以及铰接点的影响。

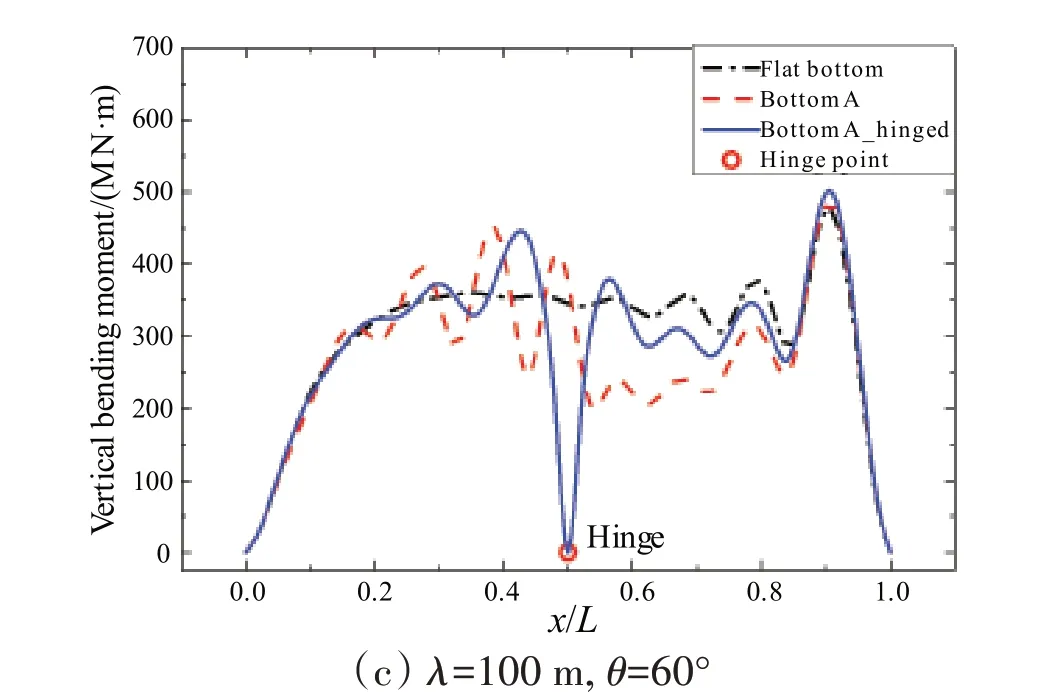
图9 不同波浪入射角下VLFS的垂向弯矩Fig.9 Vertical bending moment of VLFS at different wave angles

图10 不同波长下VLFS的垂向弯矩Fig.10 Vertical bending moment of VLFS at different wave lengths

从图10 可以看出，0°浪向下，随着入射波波长的增大，结构的最大弯矩有逐渐增大的趋势，且除400 m 波长外，其余波长出现最大弯矩的位置基本相同，靠近结构的首部。而400 m 波长下的最大弯矩出现在中部位置。此外，铰接连接的存在，主要降低了铰接点附近的弯矩。

3.3 连接件处的垂向位移及受力

图11给出了连接件处的垂向位移在两种海底环境下随入射波角度的变化情况。可以看出，非均匀海底对连接件的垂向位移存在一定影响，并且影响存在于浪向角较大的情况下，在入射波角度和波长较小时，两种海底环境下连接件处的垂向位移几乎相同，非均匀效应不明显。而随着波浪角度和波长的增加，非均匀效应逐渐增加。尤其是在横浪时，在非均匀海底环境下的连接件的垂向位移值约为均匀海底环境下的1.5倍。

图11 不同波长下连接件处的垂向位移Fig.11 Vertical displacements of connectors at different wavelengths

为了研究非均匀海底对连接件受力的影响，本文给出铰接VLFS 在均匀海底和非均匀海底（Bottom A）形式下的连接件的轴向力Fx以及垂向力Fz随入射波浪角度和波长的变化情况，如图12～13 所示。两图中，非均匀海底对连接件的轴向力和垂向力存在比较明显的影响，斜浪时连接件的受力更大，此时环境工况更恶劣。对于同一种入射波波长，连接件受力的最大值对应的浪向角在两种海底形式下基本相同，除了在λ= 200 m 时Fx在两种海底形式下最大值对应的频率不相对应，但是在这种入射波波长下，两种海底形式均在各自出现最大值对应的波浪角的位置出现极值，见图12（c）。图12表明，在均匀海底形式下，连接件的受力在横浪时是趋于零的，但由于非均匀效应的影响，在非均匀海底形式下连接件的轴向力在横浪时仍保持比较大的数值。

图12 不同波长下连接件的轴向力Fig.12 Axial force of connector at different wavelengths

由图13可以看出，在非均匀海底环境下连接件垂向力的最大值在各计算波长下均大于均匀海底环境下的受力值。当波长很短时，如λ= 50 m 时，两种海底情况下连接件的垂向力差别不大。当波长逐渐增大时，非均匀效应开始显现，两种海底形式下的连接件受力差距逐渐加大。尤其在λ= 400 m时，非均匀海底情况下连接件的垂向力大约为均匀海底情况下受力的两倍。因此，在计算连接件垂向力时，必须要考虑非均匀海底带来的影响。

图13 不同波长下连接件的垂向力Fig.13 Vertical force of connector at different wavelengths

表3给出了不同波长下连接件轴向力和垂向力受力最大值所对应的浪向角。由表3可以看出，连接件受力最大值所对应的浪向角在40°～80°的范围内，因此可以看出斜浪时连接件的受力最大，VLFS作业时应避免斜浪。

表3 连接件受力最大值所对应的浪向角Tab.3 Corresponding wave angles of maximal connector’s forces

4 结 语

采用基于离散模块思想的频域水弹性分析方法，本文研究了在不同入射波波长、入射角下，非均匀海底对铰接浮体模型的垂向位移、弯矩以及连接件受力的影响。数值计算结果表明：随着入射波波长的增大，非均匀效应逐渐增大，对结构的垂向位移、弯矩以及连接件受力的影响逐渐增大；与均匀海底相比，非均匀海底对连接件的受力影响较大，因此在连接件的设计时，必须要考虑非均匀海底带来的影响；斜浪时，连接件的轴向力和垂向力均比较大，因此，VLFS作业时应尽量避免斜浪。