ONR内倾船波浪中复原力臂非线性现象试验和数值研究
2021-06-03卜淑霞张进丰黄苗苗
卜淑霞,张进丰,黄苗苗,鲁 江,顾 民
(中国船舶科学研究中心水动力学重点实验室,江苏无锡214082)
0 引 言
国际海事组织(IMO)正在制定船舶第二代完整稳性衡准,包括参数横摇和纯稳性丧失薄弱性衡准和稳性直接评估[1]。对于水线面附近几何外形变化较大的船舶,当船中位于波峰时,复原力臂会比静水复原力臂小;当船中位于波谷时,复原力臂会比静水复原力臂大,如果波长近似船长会引起波浪复原力臂的周期性变化,而这种周期性变化是参数横摇失效模式发生的主要原因[2];如果波峰位于船舯的时间过长,会导致船舶稳性力臂减少,是纯稳性丧失失效模式发生的主要原因[3]。因此,参数横摇和纯稳性丧失失效模式的发生都与波浪中复原力臂的变化有关,故横摇复原力的变化是影响参数横摇衡准和纯稳性丧失衡准评估的关键因素,有必要开展试验和数值计算的研究,验证目前横摇复原力计算方法的可靠性,并在稳性直接评估中提出合适的计算横摇复原力的方法。
在进行本文的研究时借鉴了国际上针对波浪复原力臂的研究方法[5],将所有作用在横摇方向的力矩都转换为波浪中的横摇复原力臂,在此基础上,对比分析不同成分作用力对波浪中复原力臂变化的影响,因此,文中所述的横摇复原力臂与常规耐波性中刚性复原力臂有所不同。此时波浪中复原力臂变化主要包括两部分:由常规Froude-Krylov 力和静水力引起的成分;由辐射力和绕射力引起的成分。目前波浪稳性的研究中,Froude-Krylov力和静水力引起的成分均采用了瞬时湿表面,即考虑了非线性特征。早期的研究表明(Paulling,1961)[4],基于Froude-Krylov 力假设可以较好地预报波浪中的复原力臂,因此早期大部分研究中忽略了辐射力和绕射力引起的复原力臂的变化。
但Umeda 和Hashimoto(2005)[5]的研究表明,考虑动态辐射力和绕射力之后可以提高参数横摇的预报精度,该研究认为动态辐射力和绕射力的影响与横倾角度成线性关系,且认为与波高成线性关系。其他学者也采用线性关系开展了研究[6-9]。本文作者基于二维切片法,也研究了动态辐射力和绕射力对参数横摇预报精度的影响,考虑了动态复原力臂与横倾角度的非线性关系,采用了插值方法计算瞬时横倾角度下的动态辐射力和绕射力,但对于垂荡和纵摇则采用了频域转时域的线性方法[10];随后,针对顶浪和随浪中复原力臂的变化开展了详细的模型试验研究,并对比分析了准静态平衡法和切片法的区别[11]。Sadat-Hosseini 等[12]采用CFDSHIP-IOWA 全粘流方法研究了参数横摇现象,文中对波浪中复原力臂的变化进行了数值模拟。结果表明,复原力臂变化的非线性现象比较明显,不过文中未能研究非线性出现的原因。
为了提供更加可靠的预报方法以及考虑到二维切片法在处理垂荡和纵摇运动的局限性[13],本文作者(2019)进一步基于三维时域混合源法,建立了波浪中复原力臂的计算方法,并在速度势的求解中引入精确物面条件,首次在波浪稳性的计算中考虑物面全非线性,实现了沿瞬时湿表面积分的辐射力和绕射力的计算。针对外飘船型,详细研究了复原力臂的不同组成成分,并对比分析了已有的近似物面非线性方法和精确物面方法的区别,指出了目前横摇复原力臂计算方法的不足,尤其是高航速、高波陡的情况[14]。
基于前期的研究结论,本文进一步采用三维时域混合源法,针对ONR 内倾船型的横摇复原力臂开展了研究,重点分析了ONR内倾船型波浪中横摇复原力臂非线性现象的原因。
1 计算方法与理论模型
1.1 三维时域混合源法
船舶波浪稳性的研究属于瞬态的非线性问题,且几何的非线性特征也是非常重要的影响因素,因此研究中采用三维时域面元法求解。在面元法的具体处理中又可进一步划分为Rankine 源和时域Green 函数两种方法,考虑到Rankine 源方法中不容易处理远场边界和时域Green 函数高频振荡等问题,本文采用了三维时域混合源法求解船舶在波浪中的非线性时域运动。该方法综合了Rankine源能较好地反应近壁面大幅运动以及时域Green 函数自动满足线性自由面和远场辐射条件的优点[15-16]。该三维时域混合源法在数值求解中引入了控制面SC,将流场分为内场I 和外场II。内场I 是由船体湿表面Sb、部分自由液面Sf1和控制面SC包围的闭合区域;外场II 由控制面SC、剩余的自由液面Sf2和无穷边界S∞组成,流场分布如图1所示。
为了研究波浪中船舶的运动,采用了三个坐标系:(1)大地坐标系OXYZ:Z 轴垂直向上,X-Y 平面位于静水面,X 轴在中心面,指向船首,原点位于中心线,OXYZ 坐标系用于定义入射波,该坐标系不随船体运动;(2)惯性坐标系o′x′y′z′:初始时刻与OXYZ处于同一位置,但随船体以速度U0前进,原点位于静水面上并与重心在同一铅垂线上;(3)船体系Gxyz:随船体运动,初始时刻x - y 平行于船体静水面,坐标原点位于重心G 处。通过3 个平动和3 个转动来唯一确定船体的运动,也就是纵荡、横荡、垂荡,横摇、纵摇和艏摇。
记内场总扰动势Φ(P,t)为ΦI(P,t),那么ΦI(P,t)在大地坐标系下应该满足以下条件:


图1 混合源法流场区域划分和坐标系示意图Fig.1 Diagram of the fluid region and coordinate systems in the hybrid source method
则内场I中Rankine源的边界积分方程如下:

式中,Aij、Bij为影响系数,可以表示为
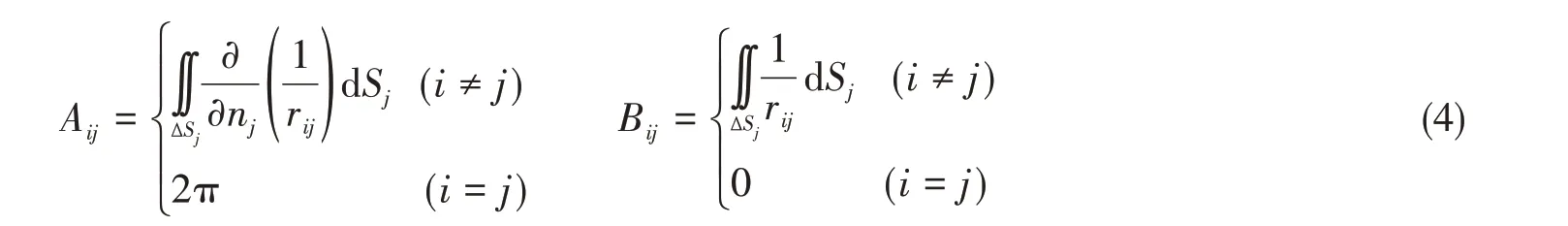
记外场总扰动势Φ(P,t)为ΦII(P,t),那么ΦII(P,t)在大地坐标系下应满足以下条件:
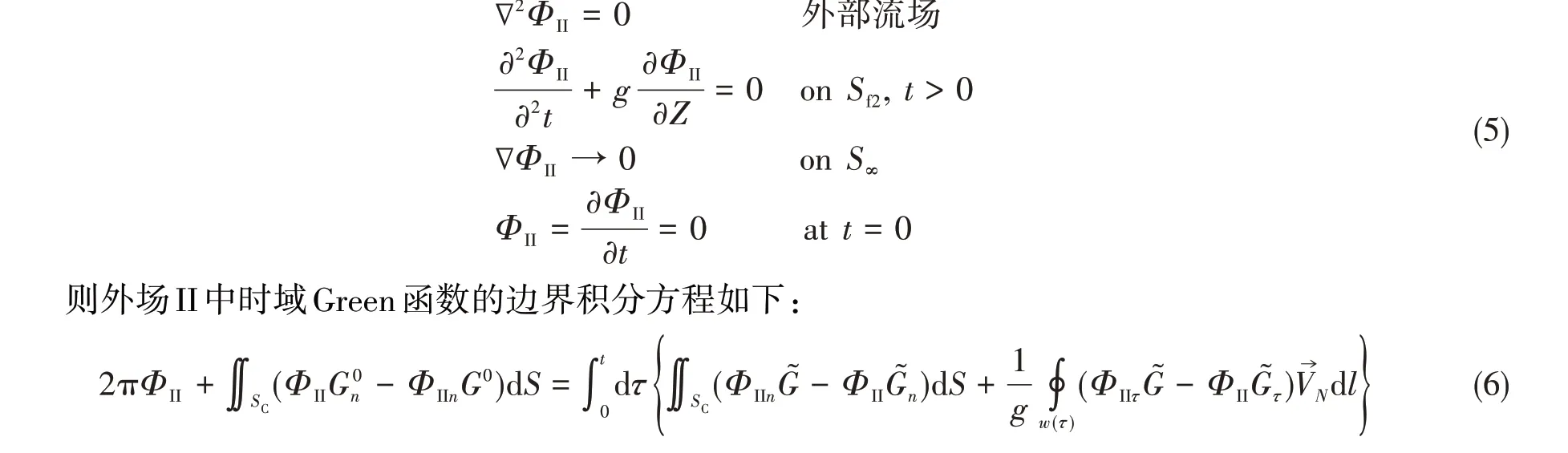
外场II 采用时域Green 函数,时域Green 函数自动满足线性自由面和远场辐射条件。因此,只需要在控制面布置面源即可,采用边界元,外场边界积分方程可以离散为

式中,Cij、Dij为矩阵系数,可以写成

引入的虚拟控制面随船体一起运动,并且在控制面上内外流场的速度势和速度势导数连续,求解内场、外场、控制面上组成离散方程,可以获得当前时刻船体湿表面积Sb上的速度势ΦI,自由表面Sf1上的速度势导数∂ΦI/∂n,以及控制面SC上的速度势ΦI和速度势导数∂ΦI/∂n。然后利用物面上的速度势ΦI,通过Bernoulli’s 方程得到船体表面的压力,利用内场I 中的自由面获得下一时刻整个流场的扰动势和下一时刻内场的速度势ΦI。
对船体平均湿表面积Sb上的源强积分即可得到船体湿表面上的扰动速度势ΦI,且已知入射波速度势Φw,最后通过Bernoulli’s方程可得到相应的压强项:

式中:∂Φw/∂t为入射波的速度势导数,在线性波浪理论中是显性已知的;∂ΦI/∂t为内场扰动势的速度势导数。
求得每个面元控制点的压力后,对每个面元积分即可求得作用于该面元上的流体作用力F 和力矩M。

1.2 理论模型
一般刚体运动具有六个自由度,但可以通过考虑一些限制条件,将其减少。首先,假设船舶在顶浪航行时航向固定,此时横荡和艏摇运动可以忽略;其次,假设船体可以保持恒定的航速,此时纵荡运动可以忽略,这时仅剩下垂荡、纵摇和横摇运动。又进一步考虑到顶浪航行时垂荡和纵摇与横摇运动存在强耦合作用,顶浪中复原力臂的变化与动态垂荡和纵摇运动有关[11,17-18],因此本文选取垂荡-横摇-纵摇相互耦合的三自由度数学模型。

式中:m 是船体质量;Ixx是船体横摇惯性矩;Iyy是船体纵摇惯性矩;Aij是船体附加质量;Bij是船体阻尼系数;ζ 是船体垂荡位移;θ 是船体纵摇运动;φ 是船体横摇运动;N1、N3分别是线性和立方项的横摇阻尼,由于横摇角度固定,故在横摇复原力臂的计算中对结果无影响;FFK+H是Froude-Krylov 力和静水力;FD是船体绕射力。船体运动的偏微分方程利用Runge-Kutta方法求解。
动稳性研究的关键在于横摇力矩求解的准确性。因此,可以通过评估不同成分在横摇力矩方向的贡献进而研究不同成分作用力的影响,为了方便计算,在研究中将所有作用在横摇方向的力/力矩转换为横摇方向的复原力臂。此时波浪中复原力臂可以进一步划分成两部分,一部分是静水和Froude-Krylov力引起的成分(GZFK),另一部分是辐射力和绕射力引起的成分(GZRD),可表示为

上述公式中,静水力和Froude-Krylov力的计算一般沿入射波与船体形成的瞬时湿表面积分,辐射力和绕射力的计算与物面条件有关[20],一般可以划分为:仅考虑初始平均湿表面的线性物面边界条件,此时辐射力和绕射力的计算沿着初始时刻的平均湿表面积分,故辐射力和绕射力在计算中保持不变;考虑瞬时平均湿表面的近似物面非线性条件,此时辐射力和绕射力的计算沿着每一时刻的平均湿表面积分;考虑船舶-波浪瞬时位置的精确物面条件,此时辐射力和绕射力的计算沿船舶-波浪瞬时相对位置形成的湿表面积分。
本文研究中采用了三种方法研究横摇复原力臂的变化:一种是仅考虑Froude-Krylov 力和静水力引起的横摇复原力臂的变化,称为GZFK。该方法中沿船舶-波浪形成的瞬时湿表面积分压力计算Froude-Krylov力和静水力,进而获得对应的横摇复原力臂:

第二种方法是在第一种方法的基础上,同时考虑Froude-Krylov 力、静水力、辐射力和绕射力引起的横摇复原力臂的变化,称为GZFK+RD,其中采用近似物面非线性条件处理辐射力和绕射力引起的复原力臂成分,也即在Laplace 初边值问题的求解中采用近似物面条件,进而得到辐射力和绕射力引起的复原力臂,示意图如图2所示。

第三种方法仍然是同时考虑Froude-Krylov力、静水力、辐射力和绕射力引起的横摇复原力臂的变化,但基于精确物面条件处理辐射力和绕射力引起的复原力臂成分,也就是每一时刻都对船体表面网格、自由面网格、控制面网格进行瞬时划分,瞬时求解Laplace 初边值问题,进而得到辐射力和绕射力引起的复原力臂,示意图如图3所示。

式中,S代表船体瞬时湿表面,Sˉ(φ)代表考虑横倾角度之后的平均湿表面,φ代表固定横倾角度。

图2 近似物面非线性条件示意图Fig.2 Diagram of the nonlinear body condition

图3 精确物面条件示意图Fig.3 Diagram of the exact body condition
2 模型试验与数值模型
2.1 模型试验
研究对象为ONR 内倾船型,该船的主要参数如表1所示,船体外形和剖面图如图4所示。可以看出该船内倾比较明显,当波峰或者波谷位于船舯时,复原力臂会与静水中有所不同,在纵浪中航行时横摇复原力臂的变化可能会非常显著,导致容易发生稳性不足的现象。因此,保证波浪中足够的稳性是该船型走向实际应用必须要解决的问题。

表1 ONR内倾船型主尺度及主要参数(缩尺比:1:40.526)Tab.1 Principal particulars of the ONR tumblehome(Scale:1:40.526)

图4 ONR内倾船型模型试验照片和船体剖面图Fig.4 Model test photo and profile of ONR tumblehome
模型试验研究在中国船舶科学研究中心耐波性水池中进行,该水池主尺度为长69 m、宽46 m、深4 m,水池相邻两边安装了先进的由伺服电机驱动的三维造波系统,可进行任意浪向下的模型试验。配置了先进的浪高仪以及自主研发的波浪力/力矩和运动响应集成测量装置,可以测量不同横倾角度下船模在波浪中横倾力臂的变化,满足试验要求。
船模采用玻璃钢(FRP)材料,船体采用整体构造,有足够的纵、横强度,保证在波浪中试验时模型不发生变形。为了保证在大倾角下船模内部不发生进水,模型整体采用水密构造,设置了三个舱盖,同时舱盖采用有机玻璃且采用密封圈以及可拆卸螺丝固定。
试验采用约束模方式,将模型固定在要求的横倾角度下,垂荡和纵摇自由,约束其它模态;采用中国船舶科学研究中心自主研发的波浪力/力矩和运动响应集成测量装置测量波浪中船模横摇复原力的变化和垂荡、纵摇运动;将一台伺服式浪高仪安装在船模重心右侧约1.5 m处,由计算机实时记录船模重心与波浪的瞬时相对位置。
2.2 数值模拟
数值模拟中,ONR 内倾船型整船体和水面以下船体网格划分如图5 所示。计算中采用线性面元网格,边界域的大小由控制面大小决定,控制面的尺寸考虑船体可能产生的兴波和波系角,采用式(18)计算,控制面的深度为4.5d,满足无限水深条件。

式中,Ld是控制面长度;Bd是控制面宽度;λ是波长,λ= U2· 2π/g。

图5 计算用的船体表面和自由面网格Fig.5 Meshes on the body and free surface used for calculation
数值模拟中船舯剖面位于内场的中心位置,数值模拟中至少得到10 个稳定的横摇周期,时间间隔为0.15 s,保证每个周期的模拟点在100个左右。
3 结果与分析
3.1 试验和计算结果对比
基于三维时域混合源法开展不同工况下波浪中复原力臂变化的计算研究。作者前期研究表明[13],在计算辐射力和绕射力时,采用精确物面条件与采用近似物面非线性条件计算得到的复原力臂幅值基本一致,精确物面可以更好地捕捉非线性现象,但采用精确物面条件计算,需要瞬时划分所有的网格,瞬时求解Laplace 初边值问题进而得到瞬时扰动速度势,计算时间过长。因此,从节省计算时间的角度出发,本文首先采用了近似物面非线性条件进行了复原力臂的计算,然后在分析非线性原因时,同时采用了两种物面条件。计算结果中,“Exp”代表模型试验结果;“GZFK”代表仅考虑Froude-Krylov(FK)力和静水力对复原力臂的贡献;“GZFK+RD”代表同时考虑FK 力、静水力以及辐射力和绕射力(R&D)对复原力臂的贡献;复原力臂代表横摇复原力臂;FK 力、静水力、辐射力和绕射力代表横摇方向的力矩。
首先,选取工况λ/Lpp= 0.8、H/λ= 0.03、Fr = 0.0、φ = 8°,时历曲线对比结果如图6(a)所示。此种工况为零航速工况,从对比结果可以看出,基于Froude-Krylov力假设的复原力臂计算结果与模型试验结果吻合较好,进一步考虑辐射力和绕射力对复原力臂的影响后,计算结果比模型试验结果稍微偏大,但整体上仍与模型试验结果吻合较好,主要是因为零航速下动态辐射力和绕射力引起的复原力成分所占的比例较小[14,19]。
针对工况λ/Lpp= 0.8、H/λ= 0.04、Fr = 0.0、φ = 8°,时历曲线对比结果如图6(b)所示。此种情况下将波陡增加到了0.04,从模型试验结果可以看出,非线性现象略有增加,模型试验中高频成分比较明显,这些高频信号一方面可能是由试验设备与水池中大桥共振引起的,一方面也可能是由复原力臂本身的非线性引起的,本文重点分析复原力臂本身的非线性成分。从对比结果可以看出:基于Froude-Krylov 力假设的复原力臂计算结果与模型试验主要幅值部分吻合较好;进一步考虑动态辐射力和绕射力影响后的GZFK+RD,幅值可以覆盖到高频信号部分。

图6 计算结果与模型试验结果对比(λ/Lpp=0.8,Fr=0.0,φ=8°)Fig.6 Comparison of the calculation results with experimental results(λ/Lpp=0.8,Fr=0.0,φ=8°)
进一步选取有航速的工况λ/Lpp= 0.8、H/λ= 0.03、Fr = 0.1、φ = 8°,对比结果如图7 所示,此种工况下航速增加到了Fr = 0.1。可以看出,随着航速的增加,复原力臂曲线越来越不符合简谐规律,模型试验中多频率叠加现象变得更加明显,也就是说,增加航速会增加复原力臂的非线性现象,这种非线性现象使得高航速下GZ 的预报十分复杂。从时历曲线可以看出,仅考虑FK 力的计算结果比模型试验结果偏小;同时考虑FK 力和R&D 之后的结果与模型试验吻合良好,可以间接地推断出GZRD的作用在不断增加,也可以证明基于Froude-Krylov 力假设不足以精确预报GZ,高航速下复原力臂多频率叠加现象主要是GZRD的影响。进一步分析FFT曲线可以看出,模型试验中包括多种频率成分,第一共振成分比较显著,这也是常规线性方法可以预报的频率成分;仅考虑FK 力的计算结果比模型试验结果偏小;同时考虑FK 力和R&D 之后,计算得到的第一共振成分和第二共振成分的结果均与模型试验结果吻合良好。

图7 计算结果与模型试验结果对比(λ/Lpp=1.0,H/λ=0.03,Fr=0.1,φ=8°)Fig.7 Comparison of the calculation results with experimental results(λ/Lpp=1.0,H/λ=0.03,Fr=0.1,φ=8°)
针对工况λ/Lpp= 1.1、H/λ= 0.03、Fr = 0.15、φ = 18°,时历曲线和FFT 分析结果如图8 所示,此种工况将航速增加到了Fr=0.15,同时将固定横倾角度从8°增加到18°,此时非线性现象也十分明显。从时历曲线对比可以看出:仅考虑FK 力的计算结果比模型试验结果小很多,误差非常大;同时考虑FK力和R&D 之后的结果,主要幅值部分与模型试验吻合良好,但模型试验中的高频成分更加明显。从FFT 分析可以看出:此种工况下,模型试验中除了第一共振成分外,第二共振成分和第三共振成分也变得十分显著;仅考虑FK 力的计算结果在第一和第二共振频率处均比模型试验结果偏小很多;同时考虑FK 和R&D 之后,计算得到的第一共振成分和第二共振成分与模型试验吻合良好,但未能捕捉到第三及其它的高频成分。

图8 计算结果与模型试验结果对比(λ/Lpp=1.1,H/λ=0.03,Fr=0.15,φ=18°)Fig.8 Comparison of the calculation results with experimental results(λ/Lpp=1.1,H/λ=0.03,Fr=0.15,φ=18°)
总体而言,从对比结果可以看出:除零航速的工况,考虑FK 力和R&D 共同作用后,预报精度都有提高,尤其是高航速、高波陡的情况,预报精度有大幅提高,说明动态辐射力和绕射力的贡献在不断增加;当非线性现象变得更加明显时,除第一共振频率外,其它共振频率的成分会更加显著。
3.2 非线性原因分析
从上述模型试验和计算结果的对比研究中发现,波浪中复原力臂的非线性现象与航速、波陡、横倾角度等都有关系:零航速下,增加波陡,非线性特征略有增加;航速增大后,增加波陡和横倾角度,非线性现象都会变得十分明显,因此本文进一步分析了非线性特征出现的原因。
3.2.1 复原力臂不同成分对比分析
选取工况λ/Lpp= 1.0、H/λ= 0.03、φ = 20°下不同的航速(Fr = 0.0、Fr = 0.1)分析复原力臂组成中不同成分所占的比重,计算结果如图9 所示。可以看出:零航速下R&D 所占的比重较少,因此基于Froude-Krylov 力假设即可预报波浪中复原力臂的变化;而有航速时,R&D 占有不可忽视的比重,因此有航速时采用常规Froude-Krylov力假设不再成立,需要进一步考虑动态辐射力和绕射力的影响,然而目前大部分的研究中均忽略了该成分。

图9 复原力臂不同成分对比(λ/Lpp=1.0,H/λ=0.03,φ=20°)Fig.9 Comparison of the different components of roll restoring arm variation(λ/Lpp=1.0,H/λ=0.03,φ=20°)
3.2.2 物面全非线性对计算结果的影响
辐射力和绕射力的计算与Laplace 初边值问题求解中的物面条件有关,上述计算中考虑到计算时间问题,因此选用了近似物面非线性条件,也就是辐射力和绕射力的计算中沿考虑横倾角度的平均湿表面积分。从计算结果可以看出,目前基于近似物面非线性条件的辐射力和绕射力计算方法可以较好地反应第一和第二共振频率成分,但未能反应第三及其它高频成分。因此,本文进一步采用精确物面条件,考虑物面全非线性,直接沿瞬时湿表面积分计算辐射力和绕射力开展了对比研究。
选取工况λ/Lpp= 1.0、H/λ= 0.03、Fr = 0.1、φ = 18°,首先对比两种物面条件的区别,图10 为辐射力和绕射力计算时两种物面条件对应的同一周期内不同时刻船舶-波浪瞬时湿表面的变化。从图中可以看出:近似物面非线性条件中,仅考虑了横倾角度,瞬时波浪与物面之间始终存在误差;精确物面条件中,每一时间都重新划分网格,瞬时捕捉船舶-波浪之间的相对位置,因此更准确地反映了船舶-波浪相对位置的变化。图11 为FK 力和静水力计算时两种物面条件对应的船舶-波浪瞬时湿表面的变化,可以看出,两种物面条件均沿船舶-波浪瞬时形成的相对位置积分物面压力。

图10 辐射力和绕射力计算时船-波相对位置的变化Fig.10 Relative position of ship-wave for the calculation of radiation and diffraction forces

图11 FK力和静水力计算时船-波相对位置的变化Fig.11 Relative position of ship-wave for the calculation of FK and hydrostatic forces
进一步对比分析采用近似物面非线性条件和精确物面条件对计算结果的影响,两种方法计算得到的时历曲线结果对比如图12所示,图中近似物面非线性条件(Nonlinear)和精确物面(Exact)条件计算得到的复原力臂幅值基本一致。进一步分析FFT曲线结果,如图13所示,首先对比近似物面非线性条件和精确物面条件计算得到的GZRD的区别,精确物面条件能反映除第一和第二共振成分之外的高频成分(图13(a)),虽然两种物面条件计算得到的GZFK基本一致(图13(b)和(c)),但同时考虑FK力和R&D 之后,相比于近似物面非线性条件,精确物面条件除了较好地计算第一和第二共振成分外,还能较好地计算模型试验结果中出现的第三和第四共振成分(图13(d)和(e))。也就说明,精确物面条件能捕捉到部分高阶频率成分,更好地反应不同复原力臂曲线中的不同频率成分,比近似物面非线性条件更为精确。

图12 近似物面非线性和精确物面时历曲线计算结果区别Fig.12 Comparison of time series calculated by approximate body condition and exact body condition in time domain

图13 近似物面非线性和精确物面FFT曲线计算结果区别Fig.13 Comparison of FFT analysis results by approximate body condition and exact body condition
3.2.3 线性理论局限性分析
进一步将时间转换到波峰相对于船长的位置,研究不同波陡下复原力臂随船-波相对位置的变化。首先是零航速工况下不同波陡的计算结果,如图14所示。从结果可以看出,仅考虑FK 力和静水力计算得到的复原力臂幅值基本与波陡成正比关系,船舯位于波峰处复原力臂最小,且复原力臂曲线呈规律性变化,此时线性假设适用,这也是大部分二维切片法可以得出的结论[11]。进一步考虑R&D作用之后,复原力臂幅值与波陡仍然呈正比关系,但复原力臂曲线出现多频率叠加现象,此时线性假设不再适用。

图14 复原力臂相对于船舶-波浪相对位置的变化(λ/Lpp=1.0,Fr=0.0,φ=10°)Fig.14 Roll restoring arm variation with the relative position of ship to wave(λ/Lpp=1.0,Fr=0.0,φ=10°)
然后,增加航速到Fr=0.15,计算结果如图15 所示,从结果可以看出,此时非线性关系变得更加明显,R&D 的作用也更加明显,说明非线性复原力臂的计算中应该考虑R&D 的影响。复原力臂随波陡的关系呈现明显的非线性变化,目前已有的基于二维切片法的研究未能证明此种现象。

图15 复原力臂相对于船舶-波浪相对位置的变化(λ/Lpp=1.0,Fr=0.15,φ=10°)Fig.15 Roll restoring arm variation with the relative position of ship to wave(λ/Lpp=1.0,Fr=0.15,φ=10°)
4 结 论
本文通过模型试验和数值计算研究了ONR 内倾船型波浪中复原力臂的变化,在速度势的求解中引入了精确物面的处理方法,实现了基于瞬时湿表面的辐射力和绕射力的计算;并从复原力臂的组成成分、采用近似物面非线性条件与精确物面条件计算结果的对比、复原力臂随船舶-波浪相对位置的变化分析了复原力臂变化中非线性特征出现的原因。研究结果表明:
(1)当航速较低、波陡较小时,复原力臂曲线呈现线性规律,基于Froude-Krylov力假设计算得到的GZFK基本与模型试验结果吻合;
(2)增加航速以及波陡,GZRD对共振频率成分的贡献不断增加,考虑FK 和R&D 共同作用后,波浪中复原力臂的预报精度有所提高,尤其在高航速、高波陡的情况下,预报精度有大幅提高;
(3)考虑辐射力和绕射力之后,可以预报模型试验中出现的部分多频率叠加的非线性现象,目前基于近似物面非线性条件的R&D 计算方法可以较好地反应第一和第二共振频率成分,基于精确物面条件的R&D计算方法可以反应第三及其它高频成分;
(4)波浪中复原力臂的非线性现象,与航速、波陡、横倾角度等都有关系,高航速、高波陡、大横倾角度下,非线性受外界影响较为明显;
(5)顶浪中,基于Froude-Krylov 假设的顶浪复原力臂预报方法不够完善,需要进一步考虑非线性辐射绕射力的影响,此结论与作者前期针对外飘船型的结论一致[15]。
