层间耦合关联对多层网络交通传输的影响

胡亚琴, 唐 明

（1. 华东师范大学 通信与电子工程学院, 上海 200241;2. 华东师范大学 物理与电子科学学院, 上海 200241）

0 引 言

当今社会是一个高速发展的信息时代, 网络无处不在, 且在生产生活中发挥着重要的作用, 如社交网络[1]、交通网络[2]等. 随着社会的发展与经济的进步, 网络中的用户量与日俱增, 网络中的数据也随之呈现出爆发式增长. 庞大的数据量会使网络中出现部分节点负荷过载, 这种超负载会逐渐向整个网络蔓延, 最终造成网络拥塞甚至网络崩溃[3]. 而现代社会人们对网络传输速度与传输质量的要求却越来越高, 因此提高网络的承载能力和传输容量非常必要且具有重要意义.

此前关于提高网络传输容量的研究大多集中于孤立的网络[4-6], 但是现实社会中的大多数基础设施并不是独立存在的, 而是相互耦合或相互依赖在一起的, 形成了多层网络, 如铁路-航空网络、公交-地铁网络. 由于多层网络模型更能实际地反映现实世界中的网络结构, 因此越来越多的学者开始研究多层网络上的动力学行为[7-12]. Aleta等[9]提出了按交通线或输运工具分层的方式, 将公共交通系统建模为多重网络模型, 并分析了9个真实的城市交通的网络结构来测试和完善模型. Guo等[10]根据随机游走模型—Lévy, 研究了一种基于多层网络的新型导航策略, 并得到了到达网络中任意节点所需的平均时间的表达式. Ma等[11]基于节点介数提出了一种改进的全局感知路由策略, 相较于最短路径和经典的全局感知路由策略, 改进的全局感知路由策略能更好地提高网络容量.

一些研究发现, 多层网络的传输容量不仅与其拓扑结构、路由策略和网络资源有关, 还与多层网络中层与层之间的耦合方式息息相关. Wu等[13]利用模拟退火(Simulated Annealing, SA)算法得到的最佳层间耦合配置, 与同配耦合、异配耦合和随机耦合相比, 其得到的耦合配置更能显著地提高多层网络的传输容量. Chen等[14]提出了一种层间反同配耦合(Anti-Assortative Coupling)机制, 并根据节点介数得出了双层网络传输容量的理论值. 本文在这些研究的基础上, 基于层间节点的度-度相关性,提出了一种中间度耦合方式: 层间节点按照度值大小进行排序, 在中间度值的节点之间首先建立连接.并且基于双层网络模型, 分别在最短路径和有效路由[15]两种经典的路由策略下, 对比同配耦合、异配耦合和随机耦合这3种耦合方式, 验证本文提出的中间度耦合方式的有效性. 验证发现, 本文的中间度耦合方式能够使多层网络中流量的分布更加均匀, 有效提升了网络的传输容量, 且数据包在网络中的平均传输时间也较小; 尤其是在层间耦合概率较低时, 即耦合成本较低时, 相较于其他3种耦合方式, 中间度耦合方式更能明显提高网络传输容量, 降低平均传输时间, 保证了网络整体的传输性能.

1 模 型

1.1 网络模型

为简化流程, 本文采用双层网络模型来进行实验, 双层网络模型的上层为A层, 下层为B层. 考虑到现实中系统大多具有无标度网络的特性, 因此A层、B层均为无标度网络. 假设层间互连的节点是一对一的, 即每一个节点至多有一条边连接到另一层网络, 层间的耦合概率定义为

首先计算网络中所有节点的度值并排序(按照A层、B层单独的网络结构), 然后将节点按照要求一一耦合. 按照度-度相关性, 本文研究了以下4种层间耦合方式.

(1)同配耦合(Assortative Coupling, AC)方式: 即正相关连接.A层、B层节点按照度值大小排列,A层度值最大的节点与B层度值最大的节点相连,A层度值第二大节点与B层度值第二大节点相连. 重复此过程, 直到层间耦合概率达到p.

(2)异配耦合(Disassortative Coupling, DC)方式: 即负相关连接.A层、B层节点按照度值大小排列,A层度值最大的节点与B层度值最小的节点相连,A层度值第二大节点与B层度值第二小节点相连. 重复此过程, 直到层间耦合概率达到p.

(3)随机耦合(Random Coupling, RC)方式: 随机选择1个A层节点和1个B层节点, 如果2节点间没有耦合链接, 则将它们连接起来; 否则, 重新随机选择节点对, 并检查是否存在链接. 重复此过程,直到层间耦合概率达到p.

(4)中间度耦合(Middle-degree Coupling, MC)方式: 将A层、B层节点按照度值大小排列,A层中间度值的节点与B层中间度值的节点相连,A层中间度值加1的节点与B层中间度值加1的节点相连,A层中间度值减1的节点与B层中间度值减1的节点相连. 重复此过程, 直到层间耦合概率达到p.值得注意的是, 当p=1 时, 中间度耦合方式与同配耦合方式相同.

1.2 交通模型

在本文中, 双层网络中的所有节点均具有主机和路由器功能, 即每个节点既能产生数据包, 也能转发数据包. 网络中的交通模型流程如下.

步骤1: 每个时间步网络中会产生R个数据包(数据包产生率), 并被随机赋予源节点、目的节点.

步骤2: 假设双层网络中每个节点的处理能力相同, 用C表示, 即每个节点每个时间步中最多可以处理C个数据包, 且数据包在层内和层间传递时每一跳的花费相同. 数据包在生成后, 被放置在节点队列长度的队尾, 按照先进先出的规则等待处理.

步骤3: 遍历所有的邻居节点, 如果邻居节点中有目的节点则直接传给目的节点, 否则数据包将按照给定的路由策略选择下一跳节点, 在网络中进行传输, 本文采用最短路径和有效路由两种经典的路由策略.

步骤4: 数据包一旦到达目的节点就会被删除, 否则在网络中继续排队等待传输.

数据包在网络中的传输过程的流程图如图1所示.

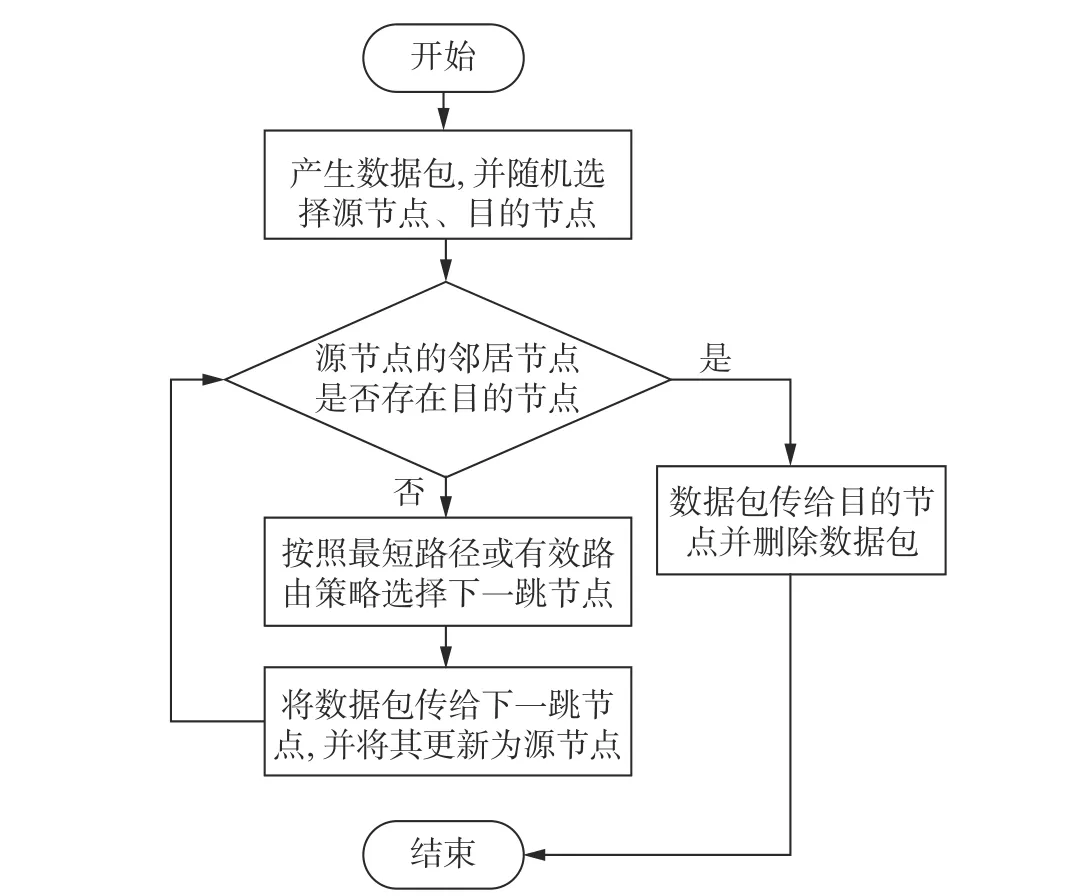
图 1 数据包传输过程的流程图Fig. 1 Flow chart of the data packet transmission process

1.3 路由策略

本文主要是研究不同的层间耦合方式对网络传输容量的影响, 数据包分别在最短路径(Shortestpath, SP)和有效路由(Efficient-routing, ER)这两种经典的路由策略下传输.

(1)最短路径(SP)策略

最短路径策略, 顾名思义, 数据包在源节点与目的节点之间选择跳数最少的路径进行传输, 如存在多条相同的最短路径, 则随机选择一条进行传递, 每个节点的路由信息保存在各自的路由表中.

(2)有效路由(ER)策略

网络中源节点s与目的节点t之间的路径, 如

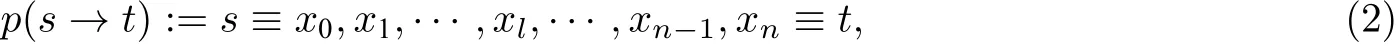
其中,xl表示第l跳节点, 源节点s经过n跳到达目的节点t. 源节点s到目的节点t的有效距离定义为

1.4 衡量指标

不同的数据包产生率会给网络带来不同的负载, 数据包产生率(每个时间步产生的数据包数量,用R表示)较低时, 网络处于自由态时, 几乎不存在数据包堆积; 随着R的增大, 网络逐渐出现拥塞现象. 这里引入网络传输阈值的概念, 网络传输阈值指的是网络从自由态向拥塞态转变时单位时间步内产生的数据包数目, 用Rc来表示. 当R＜Rc时, 网络中生成的数据包都能被及时处理, 网络中流量处于平衡状态, 无数据包堆积, 即自由态; 当R＞Rc时, 网络中生成的数据包数量大于被移除的数据包,产生大量数据包堆积, 不能及时到达目的节点, 即拥塞态; 当R=Rc时, 网络处于从自由态到拥塞态的相变状态, 网络中生成的数据包数量恰好与被移除的数据包持平, 即临界状态.

为了更好地量化网络中的拥塞程度, 我们引入序参量H来刻画, 即

本文设定每个节点的处理能力为C, 要求网络中不出现拥塞, 则每个时间步每个节点处的数据包都能被及时处理, 即qv≤C, 代入式(6)得到

其中,Ts,t(β) 表示在数据包从源节点s到达目的节点t所需要的传输时间,m表示到达目的节点的数据包数量. 数据包的平均传输时间越小, 即越快到达目的节点, 说明网络中数据包传输效率越高.

2 仿 真

本文主要是研究不同的层间耦合方式对网络传输容量的影响, 并进行了一系列的仿真实验. 考虑到实际网络的特性, 文中双层网络的上下两层均为无标度网络模型,A层、B层网络规模为NA=NB=500,〈kA〉=〈kB〉=8 , 层间耦合概率p=0.5 , 节点处理能力C=1 , 数据包分别采用最短路径和有效路由两种策略在网络中传输. 为了消除偶然误差, 本文的实验结果均由10个不同的双层网络独立仿真100次后平均得到.

数据包采用ER策略在网络中传输时, 分别研究了在AC方式、DC方式、RC方式和MC方式这4种耦合方式下, 网络的传输容量Rc与可调参数β的关系, 如图2所示. 由图2可以看到, 在每一种耦合方式下, 传输容量的仿真值与理论值几乎吻合, 其中理论值由公式(8)计算得到. 网络传输容量Rc在4种耦合方式下均呈现出先增加后减小的趋势, 且均在可调参数β约为0.6时达到最大值, 分别为114、108、111和122. 相较于AC方式、DC方式和RC方式, MC方式下的网络传输容量分别提高了7.0%、13.0%和9.9%, 这说明MC方式能使负载更均匀地分布在网络中, 更合理地分配了网络资源.

图3是数据包分别采用SP策略或ER策略在网络中传输时, 4种耦合方式下序参量H与数据包产生率R的关系. 在4种层间耦合方式下, 序参量H均随数据包产生率R呈现单调递增, 且存在相变点, 即网络传输容量Rc. 在数据包产生率较低的时候, 序参量为0, 网络处于自由态, 网络中的数据包能及时到达目的节点. 一旦数据包产生率超过阈值Rc, 序参量呈指数增加, 大量数据包堆积在网络中导致拥塞加剧. 从图3可以看出, 数据包无论采用SP策略还是ER策略传输, MC方式下的传输容量Rc均大于AC方式、DC方式和RC方式, 且随着数据包产生率逐渐增加, MC方式下的序参量增长速度相对平缓, 即网络拥塞程度增长最慢, 这也进一步说明MC方式的有效性.

数据包的平均传输时间〈T〉也是一个重要的衡量网络性能的指标, 平均传输时间越短, 说明数据包越快到达目的节点. 本文研究了在SP策略和ER策略下, 4种不同耦合方式对数据包在网络中的传输时间的影响. 在数据包产生率较低时, 网络处于自由态, 4种耦合方式下的数据包平均传输时间都较低, 说明数据包几乎都可以很快地到达目的节点. 随着数据包产生率增加, 网络中逐渐出现拥塞, 平均传输时间迅速增加, 这可能是因为部分节点过载, 数据包产生后不能被及时处理, 长时间在网络中排队等待, 导致拥塞加剧. 如图4所示, 可以看到在SP策略和ER策略下, MC方式下的数据包平均传输时间均低于AC方式、DC方式和RC方式, 这可能是因为MC方式下, 层间传输主要通过中间度节点来完成, 缓解了上下两层的中心节点的压力, 减少了等待时间, 使数据包能很快达到目的节点.

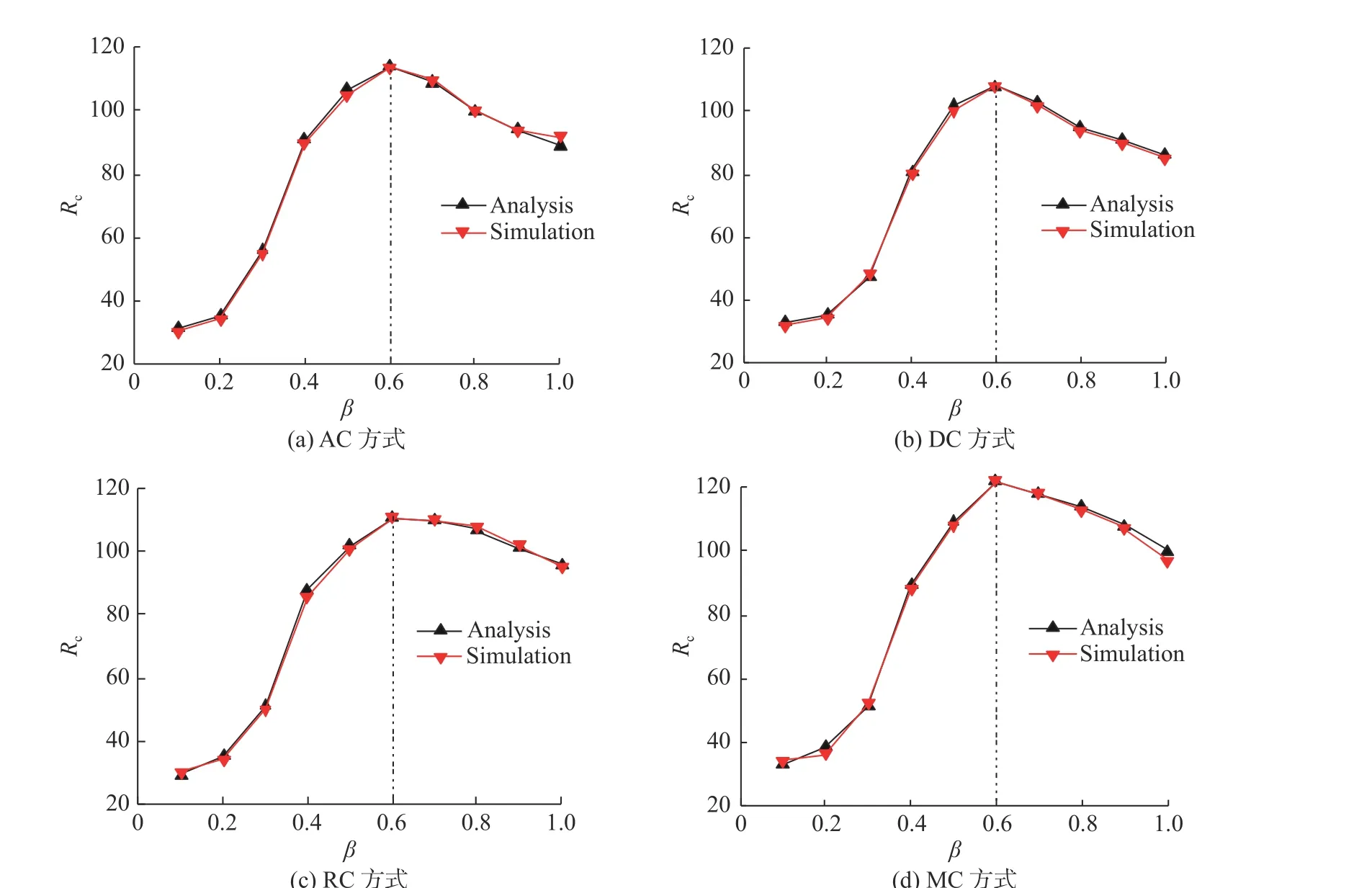
图 2 ER策略下网络传输容量 R c 与可调参数 β 的关系Fig. 2 The relationship between the traffic capacity, R c , of multilayer networks and the adjustable parameter, β , under the ER strategy

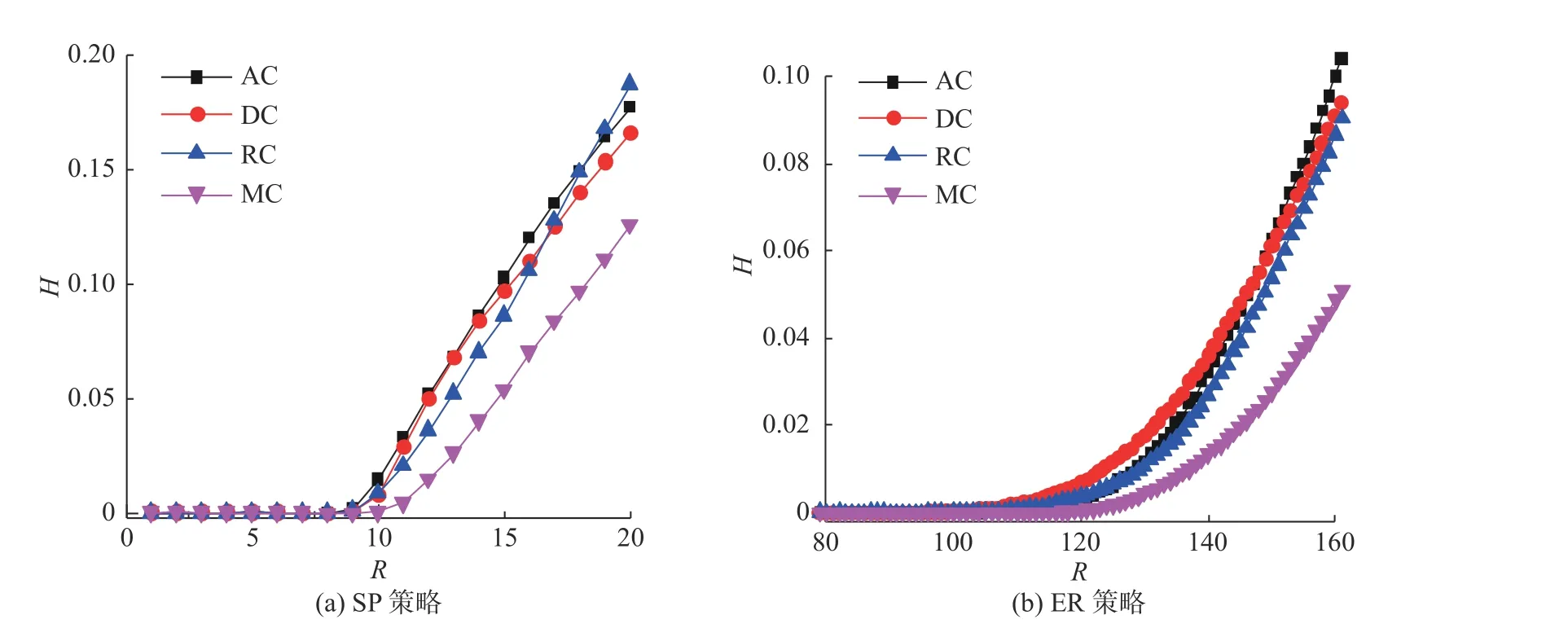
图 3 4种耦合方式下序参量 H 与数据包产生率 R 的关系Fig. 3 The relationship between the order parameter, H , and the packet generation rate,R, under four different coupling patterns

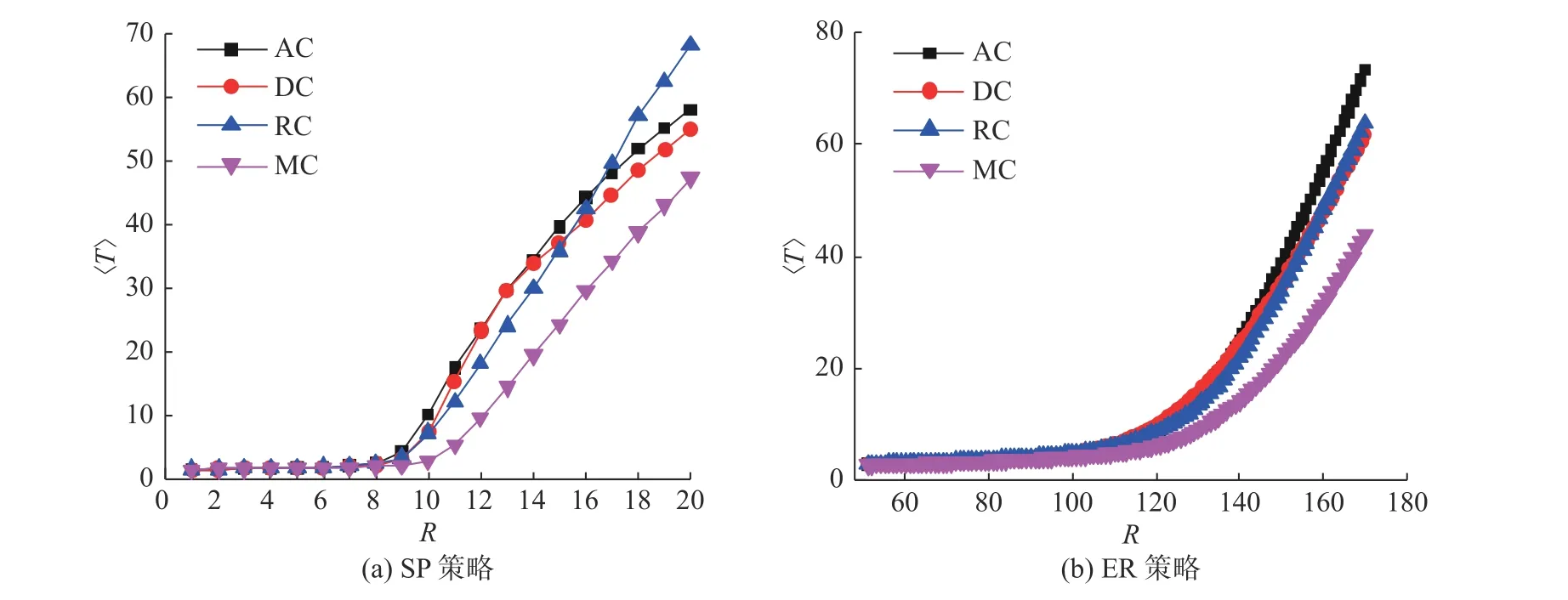
图 4 4种耦合方式下平均传输时间 〈 T〉 与数据包产生率 R 的关系Fig. 4 The relationship between the average transport time, 〈 T〉 , and the packet generation rate, R , under four different coupling patterns

本文还研究了在4种层间耦合方式下, 网络的传输容量与层间耦合概率的关系, 仿真结果如图5所示. 图5(a)中数据包采用SP策略进行传输, 可以看到与AC方式、DC方式和RC方式相比, 层间采用MC方式耦合时, 网络传输容量明显提高. 图5(b)中数据包采用ER策略进行传输, 可以看到在多层网络的层间耦合概率较低的时候, AC方式、DC方式和RC方式下网络的传输容量差异不大, 而MC方式下网络传输容量明显较高, 且随着耦合概率的增加, 4种耦合方式给传输容量造成的差异减小. 数据包无论按照SP策略还是ER策略传输, 当p=1 时, MC方式与AC方式下网络的传输容量一样. 从图5还可以看出, 在4种不同的耦合方式下, 网络的传输容量均随着耦合概率的增加而增加, 这可能是因为层间耦合概率增加, 也就是层间的链接数量增加, 数据包在层间的传输可通过更多的中继节点来完成, 从而增加了整个网络的传输容量.

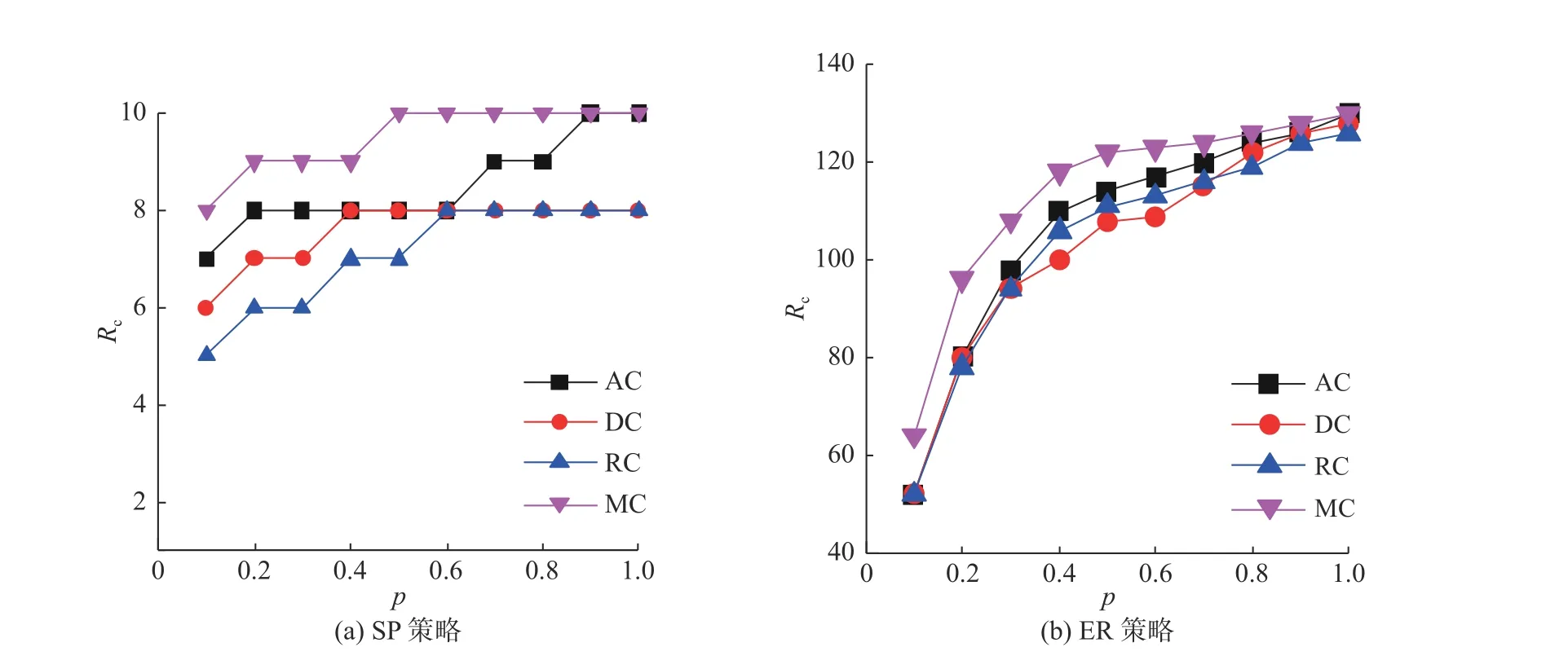
图 5 网络传输容量 R c 与层间耦合概率 p 的关系Fig. 5 The relationship between the traffic capacity, R c , of multilayer networks and the coupling probability,p

为了更好地说明层间耦合关联对多层网络传输能力的一般性影响, 本文增加了A、B均为随机网络[16]的仿真实验, 与上述相同,A层、B层的网络规模为NA=NB=500 ,〈kA〉=〈kB〉=8 , 层间耦合概率p=0.5 , 节点处理能力C=1 . 网络的传输容量Rc与可调参数β的关系如图6所示, 其中β=0 时,数据包可以理解成按照最短路径策略传输. 数据包按照SP策略传输时, AC方式、DC方式、RC方式和MC方式下, 网络最大传输容量分别为95、109、99和126; 数据包按照ER策略传输时, AC方式、DC方式、RC方式和MC方式下, 网络最大传输容量分别为184、183、188和194. 相较于其他3种耦合方式, 中间度耦合方式都能使网络的传输容量达到最大, 最大限度地使流量合理地分布在双层网络中. 同时, 与A层、B层均为无标度网络相比, 随机网络构成的双层网络的传输容量更大, 这说明了网络结构越均匀, 网络的传输容量越大, 异质网络的传输容量较低.

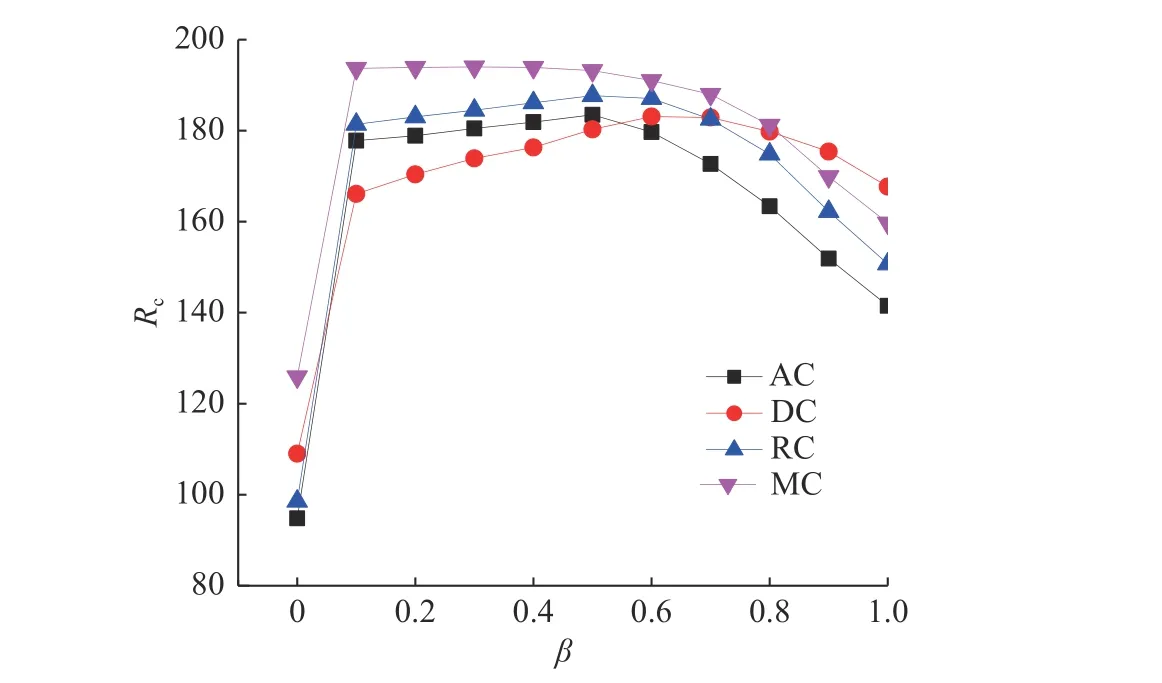
图 6 4种耦合方式下网络传输容量 R c 与可调参数 β 的关系Fig. 6 The relationship between the traffic capacity, R c , of networks and the adjustable parameters, β , under four different coupling patterns

3 结 论

为提高多层网络的传输容量, 基于层间节点的度-度相关性, 本文提出了一种中间度耦合方式, 并在BA-BA双层网络上进行了仿真验证. 本文通过推导得到的网络传输容量理论值与本文的实验结果保持了一致. 在SP策略和ER策略下, 相较于AC方式、DC方式和RC方式, MC方式均能更合理地分配网络中的负载, 提高了网络的传输容量, 有效减小了数据包的平均传输时间. 本文还发现, 随着层间耦合概率的增加, 网络的传输容量也有所提高; 数据包采用ER策略传输时, MC方式在较低耦合概率下的表现尤为突出, 即网络达到了更高的传输容量.A层、B层均为随机网络的仿真实验, 说明了中间度耦合方式能更有效地提高网络的承载能力, 且越均匀的网络的传输容量越高.