基于横向对比原理建筑用能诊断方法研讨

叶李飞

上海方圆空调通风设备与系统检测中心

0 引言

建筑、工业、交通并列为能源消耗的三大领域，也是温室气体排放的重要来源。建筑领域能源消耗占全球能源消耗的40%，且1/3的温室气体排放与建筑有关。中国近20年来能耗平均增长率为3.7%，情况更不乐观[1,2]，其中，老化建筑低效能源管理及新兴建筑快速增加是能源消耗飙升的主要原因，如不及时采取措施，将加剧能耗升高。因此，对建筑物老化产生的能源浪费采取有效诊断、提高诊断效率、实施更智能的战略是解决建筑高能耗的有效途径。

国内外已开展对建筑能耗诊断性研究，研究重点在于能耗驱动因素分析[3,4]，但该方法更适用于单栋建筑，且需对每栋建筑进行现场调研，工作量较大。近年来，BAS系统在现代建筑中得到普及，可实时统计建筑物内运行数据，利用数据挖掘技术和计算机深度学习算法（黑盒算法）分析这些数据，实现建筑能耗的预测与诊断[5-7]。但黑盒算法是借助深度数据拟合技术而不是基于热力学原理[8]。基于热力学原理与物理规律对建筑能耗进行分析仍是准确的途径。

基于能耗驱动因素分析的方法大多针对单栋建筑。若按建筑用能共性进行归类，以照明为例，办公类建筑工作日期间照明能耗较高，周末较低，而商场类建筑则差异较小[9]，按此分析，结论可能更具普适性。因此，针对不同类型建筑用能特点划分建筑类型是用能诊断的前提。为此，本文提出建立横向对比模型，根据建筑用能结构特点，提取相同特性能耗指标进行分析，以获取目标建筑的用能程度，及对其它参与对比的建筑起到诊断作用。

1 横向对比模型的建立

横向对比是对空间上并存的事物在同一时间尺度下的比较。与纵向对比同自身的历史比较不同，横向对比可同时刻画自身与其它样本的特点，对决策有着参考作用。本文建立了一种基于多数组横向对比的数学模型，用于刻画多组数据的集中趋势与分布范围。

给定一组按时间序列组成的数据点n1,n2,…,nk,其中，nk∈(tn1,tn2,…,tkl)，tkl为第k组数在1时刻的值。将每组数通过式（1）依次相加即可得到该组数据在某一时间粒度下的总和。

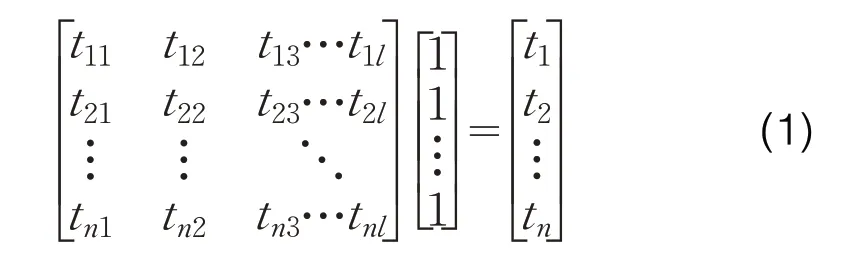
式中t1，t2，…，tn为1#数组，2#数组，…，n#数组在时间粒度内的总和。

描述数据集中趋势前需剔除异常数据，因异常数据会极大程度地降低数据质量,使分析结果发生显著变异，导致人们对问题的判断不准确，故本文提出了使用箱线图识别能耗数据异常值的办法。箱线图是一种用作显示一组数据分散情况的统计图，主要用于反映原始数据分布的特征，还可对多组数据分布特征进行比较，箱线图组成示例如图1所示。箱线图的异常值由式（2）、（3）定义。

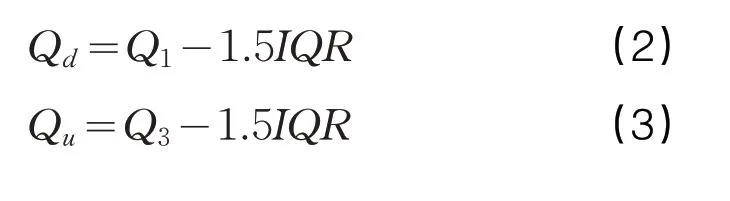
式中：

Qd：异常值下限

Qu：异常值上限

Q1：下四分位数

Q3：上四分位数

IQR：四分位距，IQR=Q3-Q1

将式（1）中的t1，t2，…，tn按从小到大的顺序排列组合后分别求出下四分位数Q1、上四分位数Q3，依据式（2）、（3）剔除异常值tk，ti…，对淘汰异常值后的数组重新命名为t"1，t"2，…，t"n。采用箱线图判断异常值可信度较高，主要原因是箱线图判断异常值的标准是以具有一定耐抗性的四分位数和四分位距为基础的，有效降低了异常值对其它数据的影响，故箱线图识别异常值的结果比较客观[10]。

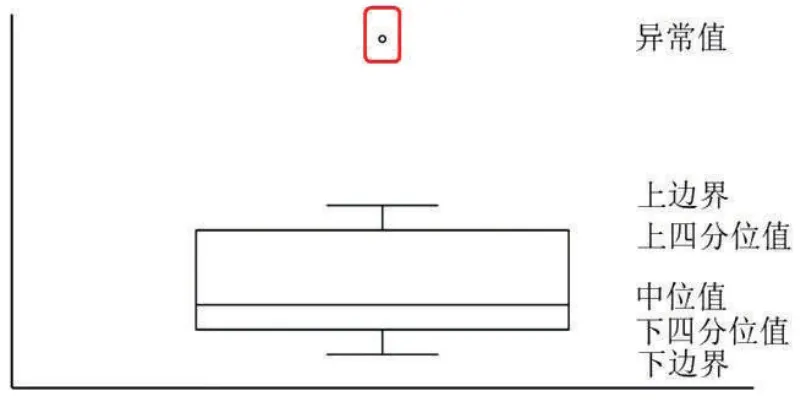
图1 箱线图组成示例

剔除异常值后，即可通过横向对比方法描述数组的离散程度及分布特征，离散程度通常用标准差衡量。经验法则表明，一组围绕平均数对称分布的数据，约有68%的数据落在±σ区间内，95%的在±2σ区间内，99%的在±3σ区间内[11]，其中，为样本平均值，σ为样本标准差。合理区间可通过实际工程的需要划分，平均值求解如式（4）所示；标准差求解如式（5）所示；参考值区间选取如式（6）、（7）所示，即tk"∈(-n1σ,+n2σ)。

2 案例分析

本文选取16栋商场类建筑作为研究对象，收集每栋建筑的总能耗量，运用第1节中的横向对比模型对这16栋建筑能耗进行横向对比，判断它们的合理用能范围，对高于临界值的进行改造，以达到降低能耗的目的。

根据现场实测，发现由于建筑本身体量不同，其能耗量值水平也不同，故需对数据进行归一化处理。归一化处理可使不同建筑体量及不同建筑在参与横向对比时占有相同的权重，以保证对比的有效性。本文采用单位建筑面积耗能量法对数据进行归一化处理。

2.1 建筑能耗监测系统用能数据获取

本案例为商场建筑，代号为SC1～SC16，建筑面积如图2所示。从BAS系统中提取16栋商场建筑用能数据作为诊断对象，将其命名为n1,n2,…,n16,任意一栋建筑的逐时能耗tnl可从BAS系统中获得，即…,nk∈(tn1,tn2,…,tnl)。BAS系统中数据记录的时间间隔是相同的，将每栋楼的能耗数据通过式（1）依次相加即可得到该栋建筑诊断时间段内的总能耗，结果如图3所示。通过式（8）可求得所有商场单位面积能耗量，结果如图4所示。

式中：

et,fyy：单位面积能耗量，kWh/m2

Et,fyy：总能耗量，kWh

A：建筑面积，m2

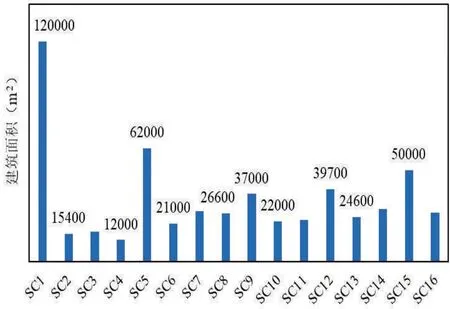
图2 16栋商场建筑面积

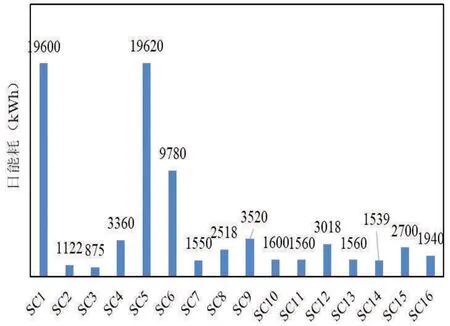
图3 16栋商场日能耗

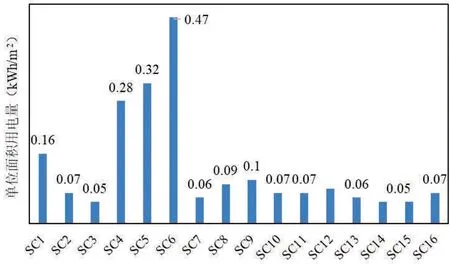
图4 所选商场建筑单位建筑面积能耗量

2.2 建筑能耗异常值判定

在实际运营中发现，能耗监测系统受限于当地网络条件，由于经常断网及网络波动造成部分上传数据存在异常值，如图5所示。为此，采用箱线图法将数据中的异常值剔除，使用其余数据来求均数，此时的均数称为截尾平均数（截尾平均数能更好地反映数据的集中趋势[12]）。得出的16栋建筑单位面积能耗箱线图如图6所示。

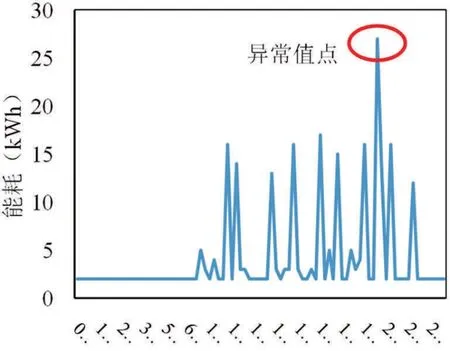
图5 某商场全天能耗监测系统记录能耗量

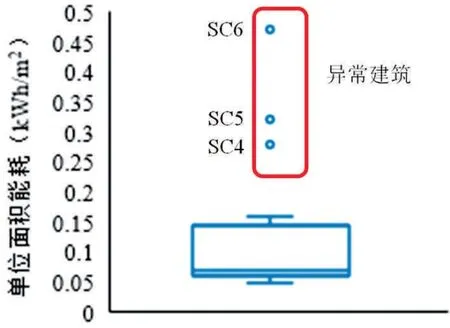
图6 16栋商场建筑单位面积能耗箱线图

通过16栋商场建筑单位建筑面积能耗横向对比箱线图可知，SC4、SC5、SC63栋建筑单位建筑面积能耗值处于异常高值范围，因此在计算合理用能区间前应先将该3栋建筑能耗数据剔除，以提高模型的鲁棒性。

2.3 单位建筑面积能耗参考值范围

剔除3栋建筑能耗数据后，依据式（4）得到其余13栋建筑单位建筑面积能耗的平均值为0.08 kW/m2，标准差为0.028。结合现场考察及建筑用能改造成本的考虑，决定将平均值加减两个标准差作为本次横向诊断的合理用能区间，即0.08±0.056 kW/m2，如图7所示。从图中可看出，除SC1、SC4、SC5、SC64栋建筑外，其余建筑单位面积能耗均在参考值范围内。

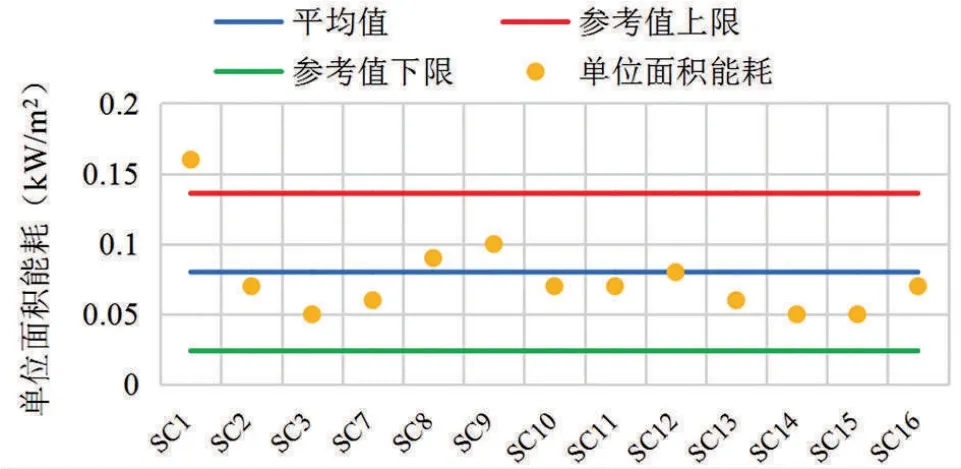
图7 建筑单位面积合理用能参考值区间

2.4 参考值范围误差分析

本文是根据16栋商场建筑进行横向对比得出的参考值范围。随着样本数量的增多，参考值范围也将发生变化，如从16栋建筑中选取3、6、9、12栋分别计算建筑用能参考值范围，得出范围如图8所示。可见随着样本数量的增多，参考值范围逐渐减小，即该模型得到的参考范围误差在逐渐减小。

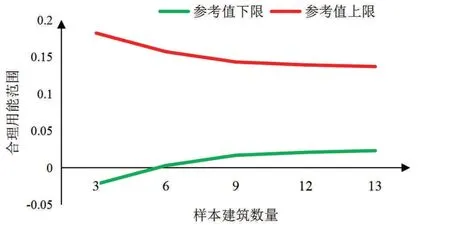
图8 建筑单位面积用能参考值图

假设该参考值下限为σ1，上限为σ2，样本建筑数量为n，从图8中可看出参考值范围与样本建筑数量呈线性关系，通过拟合得到参考值下限σ1与样本建筑数量n之间的关系式为σ1=0.0108n-0.0242，参考值上限σ2与样本建筑数量n之间的关系式为σ2=-0.0108n+0.1842，随着样本数量的增多，模型的鲁棒性逐步增强。该模型还可用于诊断新增建筑单位面积用能是否存在不合理现象。

3 结论

本文建立了一种基于横向比较原理的数学模型，该模型由多组、基于一定规则排列的数据组成，数据处理过程基于矩阵运算，得到每一组数据的总和。为避免异常值对样本整体的干扰，使用箱线图法识别并剔除异常值，再将剩余数据求平均值与标准差，根据经验法则描述数组的离散程度及分布特征。

该模型被应用到了16栋商场建筑能耗监测系统中，记录数据时间间隔均为1小时，通过模型矩阵运算可得每栋建筑在诊断时间内的总能耗量。通过箱线图剔除异常建筑，依据经验法则使用平均数和标准差计算得到16栋建筑的合理用能区间。对4栋建筑单位面积用能较高的，实地调研后认为这些建筑使用多年，部分用能设备老化，建议业主方及时更换以降低能耗。

横向比较不仅可发现被研究的建筑的用能问题，还可发现参与横向比较的建筑是否存在同样的问题，提高了研究效率。鉴于空调系统用能占据了大部分建筑能耗，可尝试将该方法推广到同类建筑的用能诊断。模型的鲁棒性将随着样本数量的增多而增强，得出的参考值适用范围也进一步扩大，为管理能源、制定用能政策提供了决策依据与参考。