融合Leader Rank和标签传播的社区发现算法∗
2021-06-02翟镇新於跃成
翟镇新 於跃成 谷 雨
(江苏科技大学计算机学院 镇江 212000)
1 引言
随着互联网技术的发展,信息量成爆炸式增长以及人与人之间的关系不断地变化,社会网络的规模也越来越大。社会网络具有信息大、无标识、社区结构等特性,其中社区结构是社会网络的基本性质,即一个网络可以分为若干个社区,社区内节点相似度较高且连接相对紧密,社区间节点相似度较低且相对稀疏。对社区的研究有很多重要的意义,例如可以找到用户组成的群组,投放相关的商业广告;挖掘群组的最新讨论话题,将其快速推荐给感兴趣的用户;预测社会网络的未来变化。这些价值实现的前提,就是社区的发现。
为了能够实现社区的划分,近代学者提出了很多优秀的社区发现方法[1~5],如基于随机游走的方法、基于结构相似性度量的聚合方法及图分割方法等,这些算法主要依据网络结构进行划分,在用于数据规模较大的社会网络时,迭代周期较长,算法复杂度较高。因此,更多学者将注重点放在提高社区的发现效率及稳定性上。
2007年,Raghavan等[6]首次将标签传播算法(LPA)运用到复杂的社会网络中用于社区发现,社区的发现效率也因此得到了显著的提高。LPA无需预先知道社区的个数,仅依据于社会网络的自身结构发现社区,算法复杂度较低,被广泛运用于大规模的社会网络中。但是LPA在每一的迭代过程中存在着随机性,致使社区发现的结果不一样,稳定性较差。
LPA产生随机性的主要起因,没有充分考虑节点自身的影响力以及将所有节点平等看待。本文引入LeaderRank[7]算法计算节点的影响力,根据LeaderRank计算的影响力值排序并采取一定的选取策略,找出网络中的关键节点,在网络节点初始化时给这些关键节点赋予唯一的标签,节点的更新顺序将根据其LeaderRank值由高到低进行更新,然后在标签传播更新的过程中,考虑节点之间的传播特性,不断迭代更新,直到大部分节点标签不在发生变化或者迭代次数达到最大,即完成社区发现。
2 相关工作
2.1 标签传播算法
标签传播算法(LPA)的基本思想:一个给定的节点x拥有n个邻居节点x1,x2,…,xn,其邻居节点都有唯一的标签,给定节点x的标签将由其邻居节点的标签信息所决定。标签传播算法可简述为以下几点。
1)节点标签初始化时,为每个节点赋予唯一的标签,用来标识节点所在的社区。
2)对图中所有的节点开始迭代更新,节点标签将会接受邻居节点的标签信息,选择邻居节点中标签数量最多的标签。当多个标签数量相同时,那么将会随机选取其中一个标签作为更新节点的标签。经过多次迭代,使得图中所有的节点趋于稳定,社区结构也将显现出来
3)根据每个节点的标签,将所有的节点进行划分,标签相同的节点将划分为同一社区。
图1为标签传播过程的一个简单案例,由图可以明显看出,标签为a的节点在接受邻居节点的标签信息后,由于标签c的节点数量为2,根据上述原理,标签为a的节点将更新为标签c。
上述算法的有两种更新方式:同步更新和异步更新。采用同步更新将会在二分图上产生循环震荡的问题。如图2所示,假设在t-1时刻如图2右图所示,t时刻如图2左图所示,如此循环下去将无法形成真正的社区。异步更新,即目标节点在t时刻的标签是依据于其部分邻居节点在t时刻的标签和另一部分邻居节点在t-1时刻的标签。
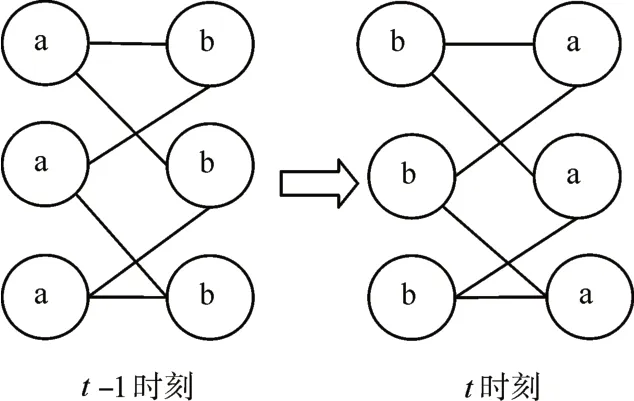
图2 标签震荡
标签传播算法具有线性的时间复杂度,以被广泛地运用于大规模的社会网络中,但是该算法在节点更新顺序和标签传播过程中存在着随机性,将会形成“无意义”的小型社区或者大型社区。
因此,为了使得标签传播算法更加高效稳定,很多研究人员进行了改进。赵卓翔等[8]在标签的传播过程中综合考虑了边的权重、每个标签的个数以及需更新节点的邻居节点的度,提出了平均权重的概念。Zhao等[9]提出了基于标签熵的标签传播算法,通过节点标签的熵值决定标签传播过程中节点的更新顺序,消除节点更新顺序中的随机性。康旭彬等[10]通过Jaccard系数计算节点之间的相似度,决定节点标签的更新选择。张鑫等[11]在标签传播过程中加入了邻居节点的影响力,从而提高社区发现的稳定性。马秀等[12]利用k-shell方法计算节点的影响力,但k-shell方法只是一种粗粒度的划分,对节点影响力的计算不够精确。Yan等[13]利用pagerank计算节点的影响力,提出了LPAP算法,但pagerank中的“跳转概率”影响着最终社区划分的稳定性。
2.2 Leader Rank算法
LeaderRank算法是对PageRank算法的优化,和PageRank算法比较,LeaderRank无需预先设置参数,即“跳转概率”,因此避免了参数的不同影响计算节点影响力的准确性,非常适合大规模的社交网络。
LeaderRank算法被用于计算网络中节点的影响力,在整个网络图中加入了一个背景节点G,该节点与原图中的所有节点均相互链接,使得整个网络图成为强连通图。
首先对背景节点G分配0个资源单位的S值(即LeaderRank值),除背景节点G以外的节点均分配1个资源单位的S值,使用式(1)计算每个节点的S值,直至达到稳态,使用式(2)将背景节点G的S值平均分给每个节点。

其中,在初始状态下除背景节点以外的节点si(0)=1,背景节点sg(0)=0。节点i与节点j之间存在链接关系,那么aij=1,反之,aij=0。kj表示节点j的度表示节点j随机游走到节点i的概率。
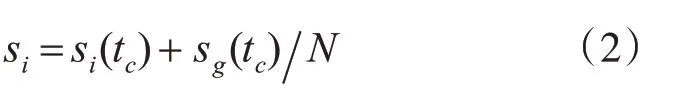
其中:tc表示稳定时刻,si(tc)表示节点i在稳定时刻的S值,sg(tc)表示背景节点G在稳定时刻的S值。
3 融合Leader Rank和标签传播的社区发现方法
本文主要是引入LeaderRank算法计算节点的影响力,从节点标签的初始化、节点更新顺序以及传播过程中节点标签的更新选择三个方面对LPA进行改进,提出了一种新的标签传播算法LLPA。整体算法流程图如图3所示。
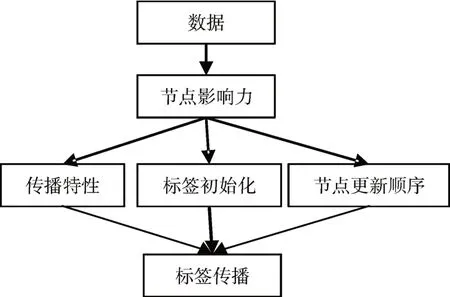
图3 算法流程图
3.1 节点初始化
在节点初始化时,LLPA算法会选择部分节点作为关键节点组成关键节点集,只为关键节点赋予唯一的标签,这些关键节点为整个网络图中影响力和重要性较大的节点。希望关键节点尽可能地辐射到网络图中所有的节点,和LPA相比,减少了不必要的判断开销,提高了效率。
将采用LeaderRank算法计算节点的S值,然后采取一定的选取策略选取出K个重要的节点。选取策略为1)关键节点的S值必须大于所有节点的平均值;2)统计每个节点的S值大于其邻居节点S值的个数lnum,若lnum与其邻居节点个数n的比值大于0.5。
3.2 节点更新顺序
为了避免图2所示的循环震荡,LLPA算法将采用异步更新的方法。网络图中有着影响力大的节点,也有影响力小的节点,在节点标签传播达到稳定状态时,影响力小的标签会被影响力大的标签所替代,若随机优先更新了影响力小的节点,这将是无意义的标签更新。
按照LeaderRank计算节点的S值,对节点进行降序排列,节点的更新顺序依据于排序结果,消除了节点更新时的随机性,减少了更新过程中无意的判断。
3.3 标签传播能力
LPA算法在传播过程中,当有多个数量相同的标签时,LPA就会随机选取其中的一个标签,这将会使得社区划分结果充满不确定性。为了降低LPA在标签传播过程中的随机性,本文将利用标签传播特性解决这一问题。
传统的标签传播算法在一定程度上考虑了标签传播特性,即假定两节点之间都是平等的,能直接相互传播。在现实的网络中,考虑到节点的影响力,根据相关参考文献[14],节点有标签传播和标签接受两种能力,影响力小的节点容易接受标签,影响力大的节点更容易将标签传播给影响力相对小的标签,其如式(3)所示。

其中ki->j表示节点i到节点j的传播能力的度量,ki->j越接近于1,节点i的影响力相对于节点j就越大,节点i的标签就更容易传播到节点j;反之,ki->j越接近于0,节点j的影响力相对于节点i较大,节点i就不易将节点传播到节点j。si表示节点i的影响力值(即LeaderRank值)。
在此基础上,对节点i的邻居中的每一个标签t计算其传播能力,如式(4)所示。
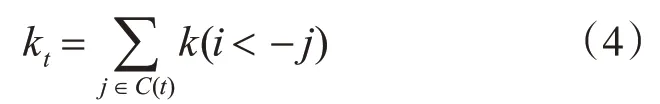
其中C(t)表示标签为t的节点集合。
故对于一个节点i来说,其标签选择如式(5)所示。

3.4 社区划分算法LLPA
LLPA算法的伪代码:
输入:图G(V,E);
输出:社区划分结果
1)计算出网络图中的关键节点列表N,为每个关键节点赋予唯一的标签;
2)计算节点的S值(即LeaderRank值),将所有节点按照S值由高到低排序;
3)迭代次数t=1;
4)按照S值的排序,更新每个节点的标签:
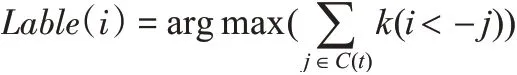
5)检查迭代次是否达到最大值或者网络中的节点标签信息不再发生变化达到稳定状态。否则在t+1时刻,返回步骤3)继续迭代更新。
LLPA算法与传统的算法相比,主要考虑节点之间的传播能力,消除标签传播过程中的随机性。选取种子节点,按顺序更新节点,减少了标签传播过程中无意的判断开销和资源的逆流。
LLPA算法的时间复杂度:选取种子节点集的时间消耗主要分为两步。计算节点的S值(即LeaderRank值)和种子节点的选取,将这两步的时间相加,即O(n2+n)。一次迭代过程(一次节点标签传播过程)所需时间为O(m),那么总的时间为O(n2+n+m)。
4 实验及结果分析
实验数据集为三个小规模的数据集和一个大规模的数据集。所有实验均采用python语言实现,实验环境为Windows10,python2.7。
4.1 实验数据
实验数据集主要选取了Karate(美国空手道联盟数据)、Football(美国橄榄球数据)、Dolphins(海豚网络数据)以及C-DBLP(计算机文献集成数据)这三个比较广泛使用的数据集。

表1 数据集参数
4.2 社区划分评价标准
1)模块度[15]。复杂网络划分社区质量的评判指标,其定义为假定一个复杂网络被划分为n个社区,定义一个n*n的对称矩阵a,那么对称矩阵中元素aij表示社区i和社区j之间相互连接边的数量与总边数的比例,表示在同一个社区内节点之间边的数量与总边数的比例,表示所有与社区i内的节点存在相互连接的边的数量与总边数的比例。
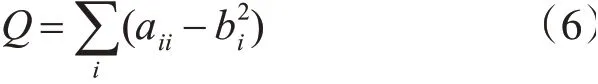
2)NMI[16]。标准化互信息(NMI),衡量一个方法下社区划分结果与标准划分的社区相似程度,其公式如下:
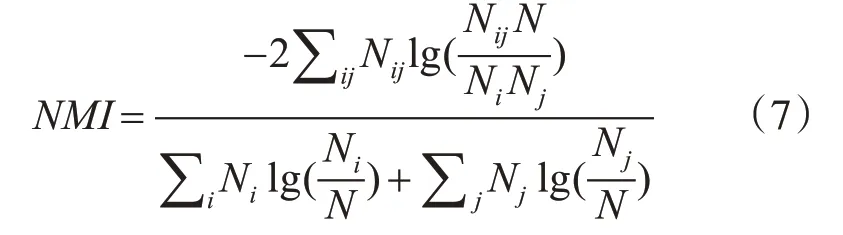
其中,N表示划分出的社区集合与真实社区集合的并集,Nij表示社区i和社区j的交集即公共的节点,Nj表示N中第j行所有元素的集合。
4.3 实验结果及分析
4.3.1 实验1-小规模数据实验
实验1主要选取了Karate、Football、Dolphins三种常用的真实数据集,对LPA算法、LPAP算法以及本文所提出的LLPA算法进行测试。表2为数据集在三种算法上进行测试得出Q值,表3为数据集在三种算法上进行测试得出NMI值。
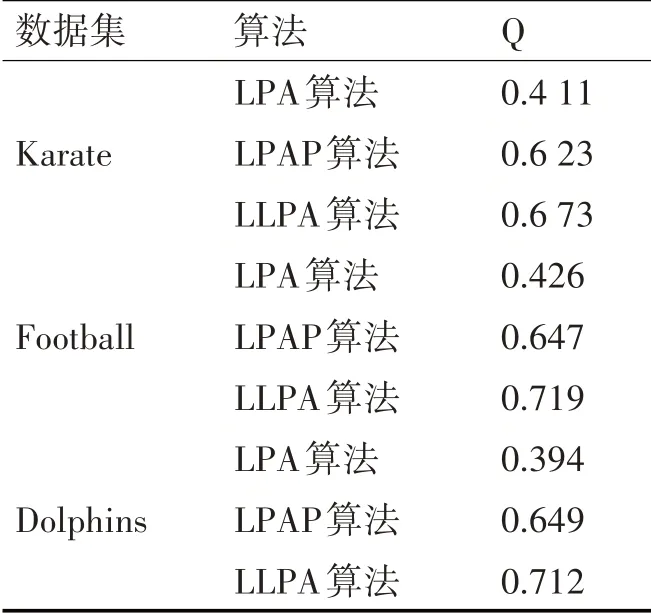
表2 小规模数据集实验得出的Q值
从表2和表3可以清晰地看出,在三个真实的数据集中,LPAP算法和LLPA算法本在Q值和NMI值上均优于传统的LPA算法,因数据集数据量小网络结构较为简单,LPAP和LLPA整体差距较小,但本文LLPA算法的Q值和NMI值依然是最大的,即社区划分结果是最好的。
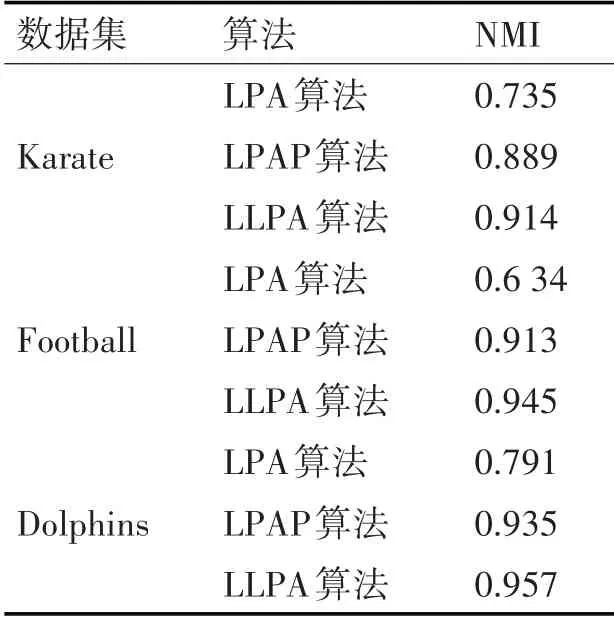
表3 小规模数据集实验得出的NMI值
4.3.2 实验2-大规模数据实验
实验2采用C-DBLP数据集,分别运行LPA算法、LPAP算法、LLPA算法,最大迭代次数均设置为100。实验结果如表4所示。
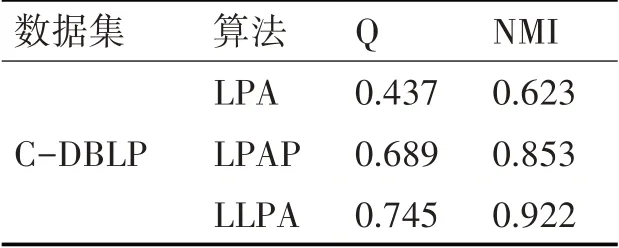
表4 大规模数据实验得出的Q值和NMI值
从表4可以看出,在数据量较大数据结构较为复杂的数据集上,传统标签传播算法发现社区的质量是最低的,LPAP、LLPA算法依然有着很好的优势,由于pagerank算法存在“跳转概率”参数的影响,使得LLPA在各项指标方面优于LPAP。经上述实验证明,LLPA算法能够有效地提高社区发现的质量,有着较强的稳定性。
5 结语
本文分析了标签传播算法的优缺点,从节点影响力入手,不再平等地对待每个节点。借鉴Lead⁃erRank算法,计算每个节点的影响力。在此基础上采取一定的选取策略,获取关键节点列表并为关键节点赋予唯一的标签。节点的更新顺序依据于节点的影响力,优先更新影响力较大的节点,防止资源的“逆流”。在标签的传播过程中,考虑节点之间的传播特性,消除节点标签更新过程中的随机性,使得最终社区的划分更加稳定。
