碳纤维复合材料纵横向拉压强度性能预测

刘佳鑫，林再文，邹志伟，程显贺，苗壮

(长春长光宇航复合材料有限公司，长春 130000)

0 引言

随着航空、航天、汽车等各领域对结构效率和轻量化的要求日渐提升，碳纤维复合材料得到了广泛应用。其优点明显，比强度、比刚度高，可设计性强，同时抗疲劳、耐腐蚀等性能好[1]。目前，对于复合材料强度的研究多集中于单向板和层合板。单向板即由单一纤维方向制备的预浸料单一角度铺放成型的板材结构，如图1所示；层合板即由预浸料根据预先设计的铺层角度依次序铺放成型的板材结构，如图2所示。

图1 单向板

图2 层合板

力学性能是复合材料结构设计过程的关键，基于复合材料经典层合板理论[2]及数值仿真软件在工程上的广泛应用，解析解和数值仿真解已能对复合材料层合板的刚度和热胀性能进行较高精度的预测。但由于复合材料失效准则多样，损伤机理复杂，对于复合材料层合板的强度性能，目前仍没有一个较为高效且通用的预测方案[3]。常用的复合材料失效准则可分为两类[4]，一类不区分失效方式，如经典的Tsai-Wu准则和Tsai-Hill准则；另一类区分失效方式，如最大应力/应变准则和Hashin准则。

本文应用试验与仿真相结合的方式，对碳纤维复合材料单向板及层合板的强度性能进行了研究。分别对产品随炉的单向板试样和层合板试样进行了力学性能测试。据此建立了有限元仿真模型。分别基于Tsai-wu准则和Hashin准则，对单向板及层合板的强度极限进行了计算，并通过试验结果对仿真模型的预测精度进行了验证。同时，给出了Hashin准则四种失效模式时能量耗散的经验公式，并将Tsai-wu准则与Hashin准则下的计算结果进行了分析对比。该研究体系与成果为工程上复合材料结构的研发设计和强度预测提供了建议与参考。

1 试验研究

为研究复合材料的强度性能，对某复合材料产品的随炉试样进行了力学性能测试。试件材料为T800碳纤维/氰酸酯，试验分为单向板力学性能测试和层合板力学性能测试。试件结构如图3所示。

图3 试件尺寸示意图

1.1 单向板力学测试

测试在DNS100电子万能试验机上进行，加载方式为位移加载，加载速率为2 mm/min，试验机如图4所示。试验工况包括单向板试样的纵向拉伸、纵向压缩、横向拉伸和横向压缩，拉伸试验按GB/T 3354—1999进行测定，压缩试验按GB/T 3856—2005进行测定。进行拉伸试验时，试验设备还包括拉伸夹具、加强片和测量试件变形的引伸计；进行压缩试验时，试验设备还包括压缩夹具、静态应变仪、电阻应变片和加强片，如图5。加强片为铝合金板，直接胶接在试件上。

图4 试验机

图5 试验设备

各工况下试件的尺寸及铺层见表1，铺层0 °方向均为试件长度方向。

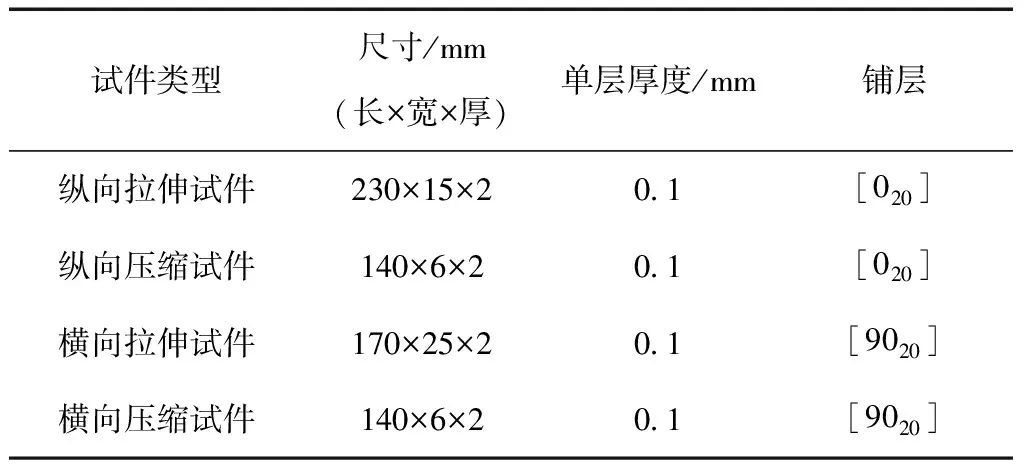
表1 单向板测试试件尺寸及铺层

1.2 单向板试验结果

各个工况分别进行5组试验，由测得的加载载荷及试件形变，可以得到试件的应力、应变及弹性模量，计算方法如下：

弹性模量：

(1)

式中：b——试件宽度；

d——试件厚度；

F——加载力；

L0——试件原长；

ΔL——试件变形量。

对各工况5组试验结果取平均值，得到四种工况单向板试验结果(表2)。单向板试件纵向拉伸断裂后，纤维呈散状；横向拉伸断口齐整；纵向压缩试件断口呈不规则锯齿状；横向压缩断口为齐整的斜面，如图6所示。

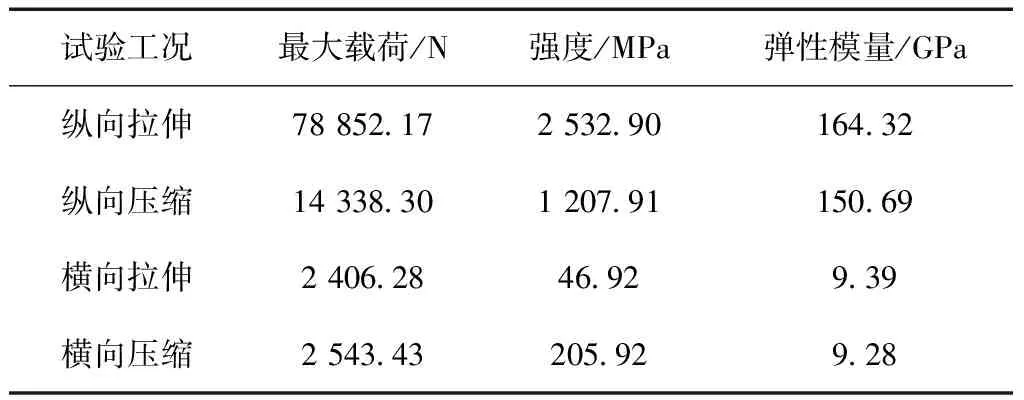
表2 单向板试验结果

图6 试件断裂面

1.3 层合板力学测试

层合板各工况测试系统和试验设备与单向板一致，同样，拉伸试验按GB/T 3354—1999进行测定，压缩试验按GB/T 3856—2005进行测定。各工况试件尺寸见表3，各工况层合板试件铺层顺序均为[0/+45/0/-45/0/902/0/+45/0/-45/0/902/0/+45/0/-45/0]，共19层，单层厚度0.1 mm。

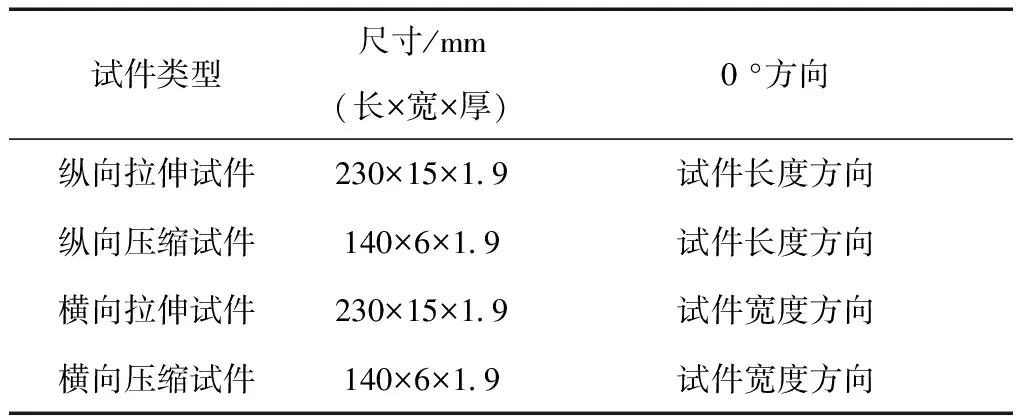
表3 层合板测试试件尺寸

1.4 层合板试验结果

各工况分别进行5组试验，得到试件的应力、应变及弹性模量。对各工况5组试验结果取平均值，得到的四种工况层合板试验结果(表4)。层合板试件断裂面较为复杂，由拉伸和压缩试件断裂面观察，多是由于沿试件长度方向的铺层全部断裂后导致的试件整体断裂，各工况试件断裂面如图7所示。

表4 层合板试验结果

图7 试件断裂面

2 仿真研究

工程中结构件一般尺寸较大、结构多样、载荷复杂，通过理论计算及试验对其进行考核难度较大、效率较低，因此有限元法被广泛应用于结构设计过程中的力学性能校核。

2.1 仿真建模及材料参数

根据单向板和层合板试件的尺寸及试验状态，采用壳单元建立有限元模型，如图8所示。根据工况分别赋予与单向板试件或层合板试件一致的复合材料铺层，模型一端固支，另一端以位移加载，加载速率为2 mm/min。

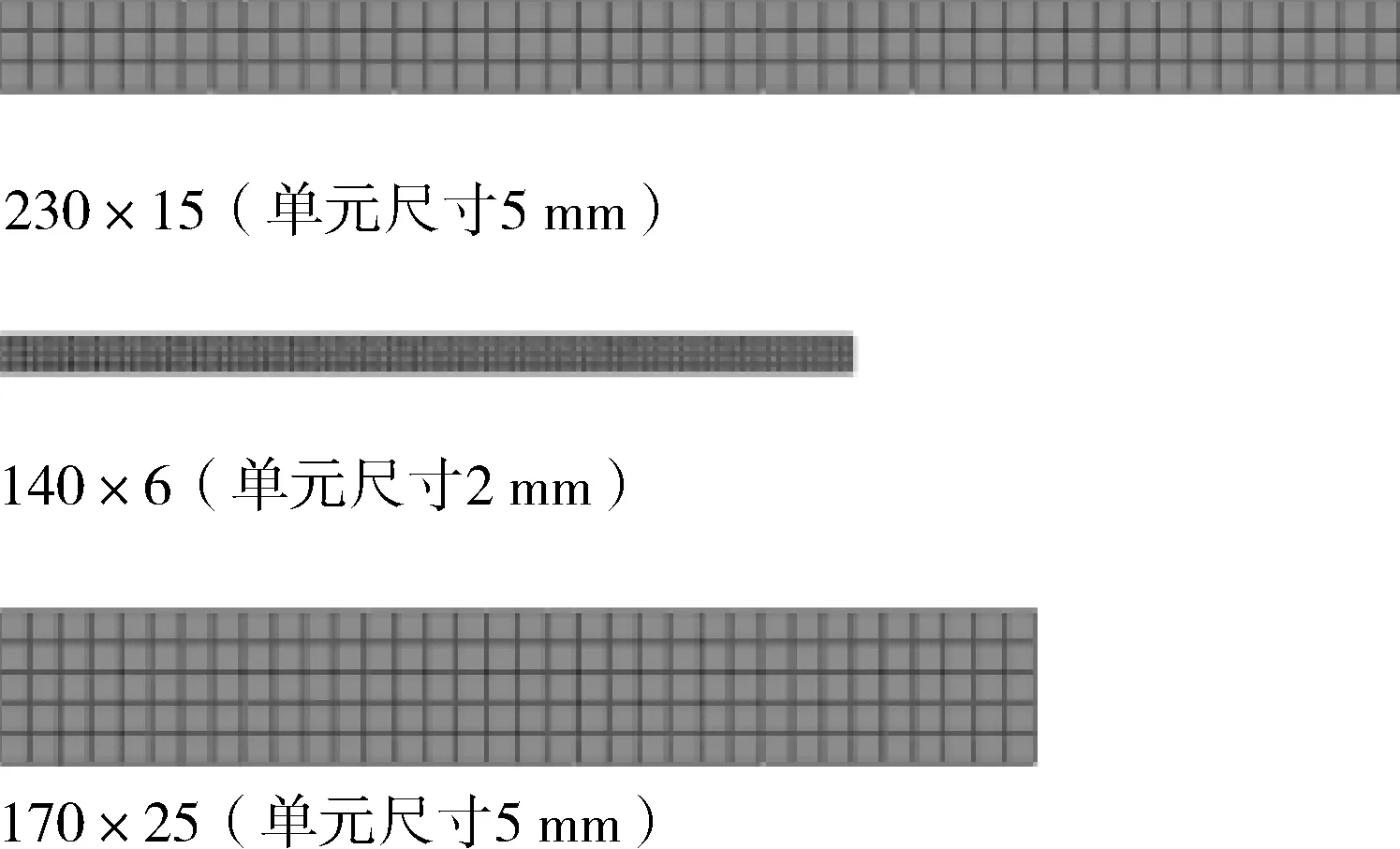
图8 试件有限元模型

以单向板试验结果确定仿真分析中单层复合材料的正交各向异性弹性及强度属性，材料参数见表5。当基于Hashin准则进行强度预测时，需要计算每种模式下完全损伤时的能量耗散，文中给出了一个计算能量耗散的经验公式，并通过仿真计算进行了验证。由于碳纤维及树脂多属于脆性材料，因此其刚度退化阶段较短，总结得到能量耗散经验公式如下：

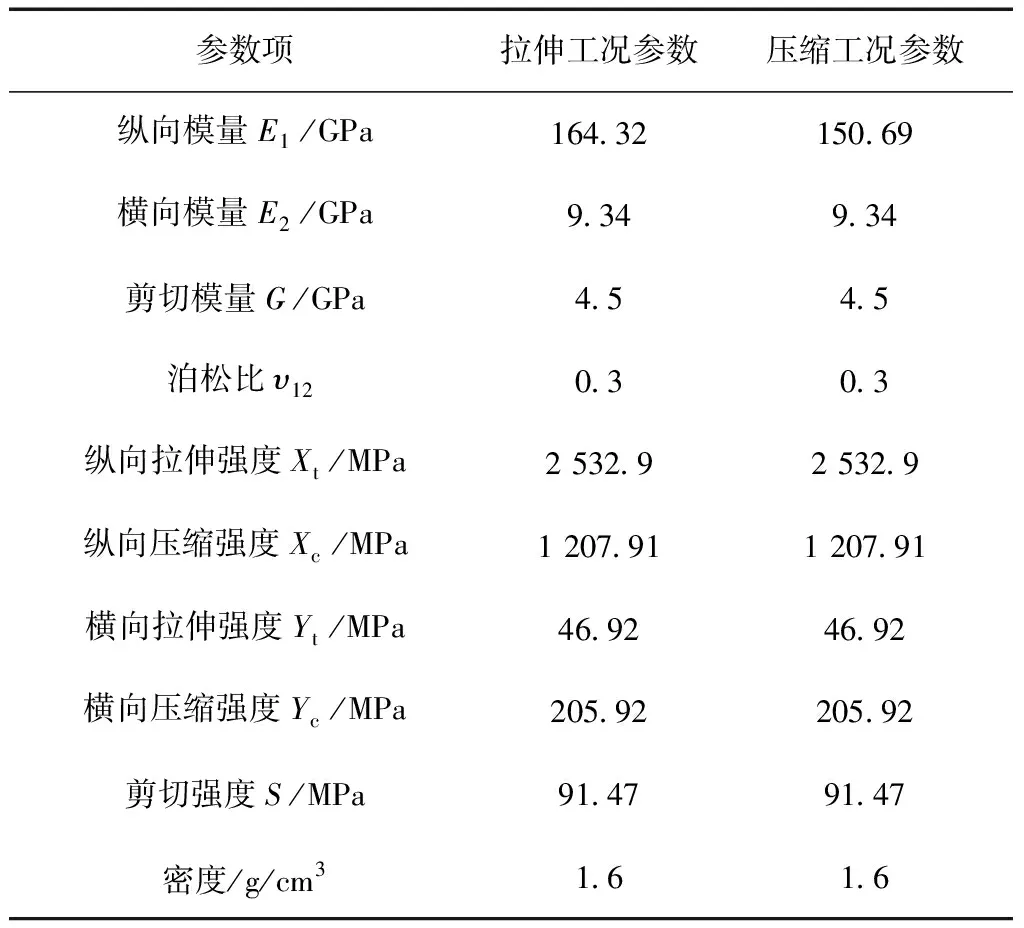
表5 弹性及强度材料参数

(2)

式中：P——能量；

X——该损伤模式下的强度；

E——该模式下的弹性模量；

Lc——有限元网格在拉伸或压缩方向上的尺寸。

由此，得到各模式下的能量耗散见表6。

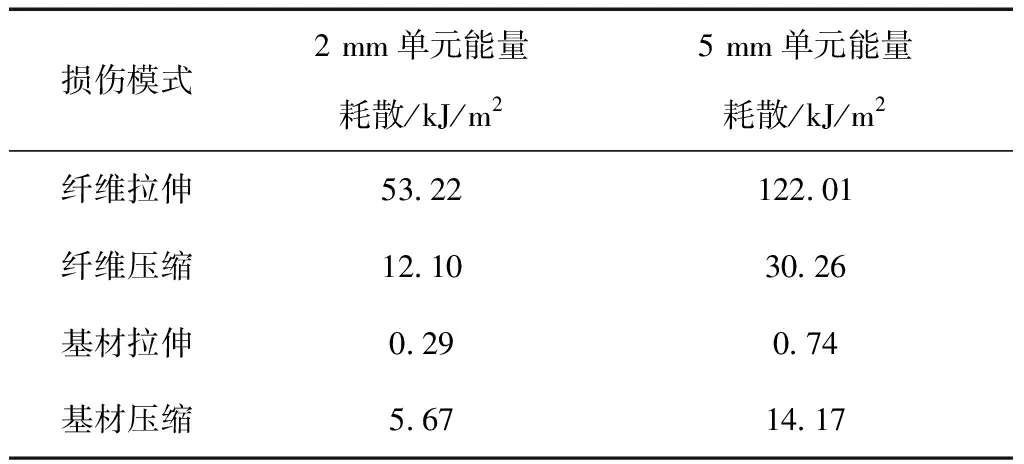
表6 各模式下能量耗散参数

2.2 基于Tsai-Wu准则计算结果

Tsai-Wu准则常用于复合材料结构前期设计中静力学、动力学的强度校核。一般认为，当结构中任一层Tsai-Wu值≥1，复合材料结构即发生失效。基于Tsai-Wu准则得到的单向板及层合板仿真计算结果见表7。单向板及层合板各个工况失效时结构Tsai-Wu值云图如图9、图10所示。其中，弹性模量仿真计算结果由式(3)得到：

表7 基于Tsai-Wu准则仿真计算结果

图9 单向板各工况Tsai-Wu值云图

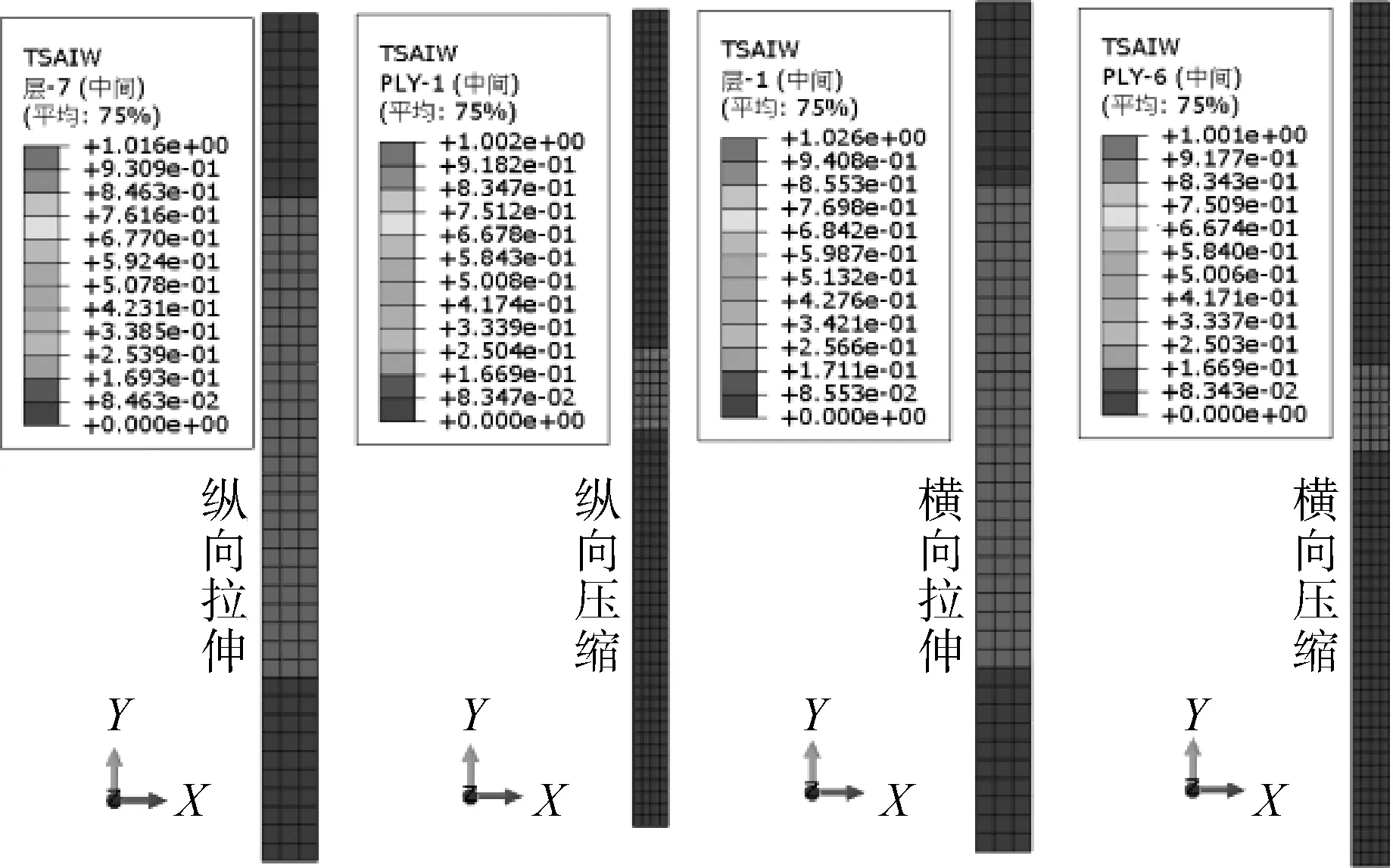
图10 层合板各工况Tsai-Wu值云图

(3)

式中:F——最大载荷仿真值；

A——仿真模型截面积；

Δl——仿真模型长度变化值；

l——仿真模型原长。

根据计算结果，层合板纵向拉伸和横向拉伸工况时，首层出现破坏的是沿试件宽度方向的铺层；层合板纵向压缩和横向压缩工况时，首层出现破坏的是沿试件长度方向的铺层。

2.3 基于Hashin准则计算结果

当基于Hashin准则时，纤维拉伸损伤、纤维压缩损伤、基体拉伸损伤和基体压缩损伤相互独立，可以只出现单个损伤模式，也可同时出现多个损伤模式。当某个损伤模式达到损伤初始值时，材料即出现该方向上的刚度退化。基于Hashin准则得到的单向板及层合板仿真计算结果见表8。

表8 基于Hashin准则仿真计算结果

根据计算结果，层合板纵向拉伸和横向拉伸工况时，在试件彻底失效之前出现两次刚度退化，分别对应图11和图12中力-位移曲线的两次斜率下降。首次刚度退化为沿试件宽度方向的铺层发生基体拉伸失效，第二次刚度退化为45 °铺层发生基体拉伸失效，最终试件长度方向铺层出现纤维拉伸损伤，试件长度方向刚度大幅退化，加载力断崖式下降，试件完全破坏。层合板纵向压缩和横向压缩工况时，首次发生刚度退化的是沿试件长度方向铺层的纤维压缩失效模式，并直接导致试件加载力卸载；在随后极小的位移载荷内，试件依次发生45 °铺层的纤维压缩失效、沿宽度铺层的基体压缩失效，最后发生45 °铺层的基体压缩失效。

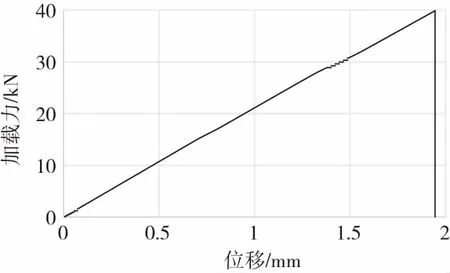
图11 层合板纵向拉伸力-位移曲线

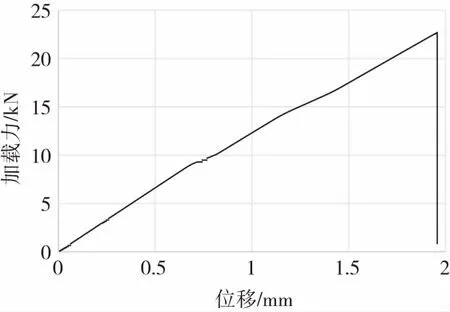
图12 层合板横向拉伸力-位移曲线

2.4 计算结果分析对比

根据仿真分析计算结果，基于Tsai-Wu准则与基于Hashin准则的各工况弹性模量计算结果一致，这是由于在模型出现损伤之前，计算均遵循正交各向异性弹性理论，而试件强度计算结果则有所差异，基于两种强度理论的最大加载力计算结果与试验结果的对比见表9。需要说明的是，各个压缩工况中，试件均未出现屈曲失稳破坏。

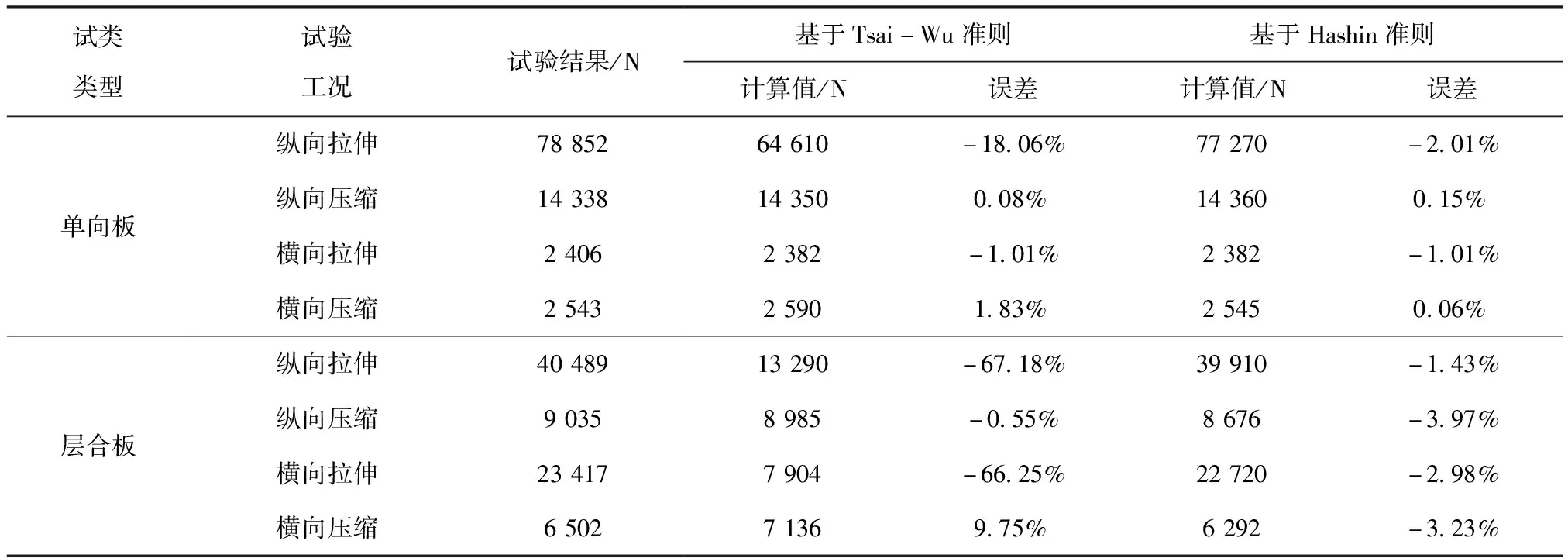
表9 最大加载力仿真与试验结果对比

对于单向板：纵向拉伸时，Hashin准则结果与试验结果吻合较好，而Tsai-Wu准则结果相对试验结果大幅偏小。这表明纤维拉伸强度在Tsai-Wu准则失效判据中所占比例较大，对Tsai-Wu值影响较大，Tsai-Wu准则对于纤维拉伸方向的强度判断较为保守。纵向压缩、横向拉伸和横向压缩时，Tsai-Wu准则结果与Hashin准则结果十分接近，同时均与试验结果吻合较好，误差较小。

对于层合板：纵向拉伸和横向拉伸时，Hashin准则结果与试验值对应较好，误差较小，且失效模式与试验完全一致，即试件长度方向铺层的纤维拉伸失效；而Tsai-Wu准则的强度预测结果大幅小于试验值，这是由于在层合板拉伸试验中，首先出现的是试件宽度方向铺层的基体拉伸损伤，此时根据Tsai-Wu准则，认定结构破坏，而实际上，此时试件在长度方向上刚度降低，但仍可以继续承载。纵向压缩、横向压缩时，Hashin准则结果与试验值同样对应较好，其失效模式为试件长度方向铺层的纤维压缩失效，与试验一致；此时Tsai-Wu准则结果与试验结果也对应较好，但高于Hashin准则，甚至高于试验值，对于试件的强度预测略微激进。

综合对比，无论是单向板还是层合板，基于Hashin准则的强度预测结果均能与试验值对应，且刚度退化方式与失效模式均与试验一致，误差较小，可以很好地预测层合板的纵向拉伸、压缩和横向拉伸、压缩的强度极限值；基于Tsai-Wu准则对层合板的强度进行预测时，拉伸时计算结果大幅偏小，压缩时结果略微偏大，总体来看强度计算结果较为保守。在Tsai-Wu值小于1时，复合材料层合板内部各层不会发生任何模式的损伤。综合考虑，在实际应用中，Tsai-Wu准则更适合于复合材料结构设计过程中的强度校核，保证复合材料的强度及刚度性能；而Hashin准则更适合于必要时复合材料结构极限承载能力的预测，但达到破坏极限之前，复合材料结构内部可能已发生了某些模式的损伤。

3 结论

(1)根据试验结果，复合材料结构的主要承载能力来自于受载方向的纤维，当沿受载方向的铺层全部发生损伤或断裂时，结构承载能力急剧下降，伴随着结构其余方向铺层相继失效，结构破坏。

(2)基于Tsai-Wu准则和Hashin准则进行了强度仿真模拟，Tsai-Wu准则不区分具体失效模式，是复合材料强度的综合考量指标，而Hashin准则区分复合材料的失效模式，并在损伤初始后进行刚度退化，与实际状态更为接近。

(3)给出了基于Hashin准则的复合材料断裂能计算经验公式：

式中：P——断裂能；

X——强度值；

E——弹性模量；

Lc——有限元网格在拉伸或压缩方向上的尺寸。

(4)实际工程应用中，Tsai-Wu准则更适于复合材料结构研发设计过程中的强度校核，结果较为保守并充分保证了结构的刚度、强度性能；Hashin准则更适合于复合材料结构极限承载能力的预测，强度仿真计算结果与试验实测值保持了高度的一致性，预测精度较高。本文的研究和结论为今后复合材料结构强度的预测提供了建议与参考。