基于贝叶斯-零膨胀负二项模型的森林火灾发生预测研究

（中国林业科学研究院 资源信息研究所，北京 100091）

森林火灾带来的危害一次次警醒人们应该全面了解森林火灾以及导致火灾发生的影响因素，森林火灾的发生通常是受火险天气、树种条件、可燃物和地形条件等要素综合作用的效果，其中火险天气与森林火灾的发生关系最为密切。火险天气是一种特殊的气象状况，在此种天气下极有利于引发森林火灾。火险天气中能够影响林火发生的气象因子包括风速、空气相对湿度、气温和降水等，这些气象因子也是判断当地防火期开始和结束的重要依据[1-2]。研究林火发生与气象因子之间的关系，可帮助管理者根据气象变化的情况采取相应的防范措施，同时也能准确监测林火发生后的动态变化规律，更加有的放矢地进行森林防火工作，减少火灾造成的危害。

以往研究森林火灾与气象因子关系模拟的分析方法中，采用非线性（线性）回归和简单的定性描述两种方法较多。但是在实际研究中，相同气象条件下林火发生次数要远远低于未发生次数，即模型中未发生事件出现大量为零的情况，此时模型效果就相对差了许多，还会给分析结果带来失真的解释[3-4]。郭福涛等[5]引入计数模型，包括负二项和零膨胀负二项回归模型研究分析1980—2005年大兴安岭林区气象因素发生与雷击火间的联系，并与传统的方法进行了对比，结果表明模型对雷击火发生次数的预测能力强，但结果存在着一定的不确定性。Xiao等[6]在负二项和零膨胀负二项回归模型的基础上引入随机效应参数分析森林火灾区域的差异，但是结果所拟合出来的森林火灾发生次数存在着一定的不确定性。

虽然人们对森林火灾发生过程和气象因子之间的研究模拟日趋复杂，但是依然不能解决森林火灾发生与气象因子关系模型的不确定性问题。目前，贝叶斯方法是基于贝叶斯理论发展起来的，它不仅是一种解决统计问题和系统阐述问题的方法[7-10]，也是一种评价模型不确定性的好方法，并已广泛应用于生态、水文、医疗、环境等多种研究领域。贝叶斯在林业领域也常被用到，比如用于研究直径生长模型、地上生物量模型等领域。Peter等[11]利用最大似然法和贝叶斯法比较研究树木直径的生长规律，通过贝叶斯方法估算出树木生长-死亡率函数，以此来预测树木的死亡率，贝叶斯法在此领域的应用克服了传统调查方法中所存在的缺限。张雄清等[12]通过贝叶斯法估计杉木林分断面积生长模型，发现预测精度的可靠性远远优于传统方法。张雄清等[13]还利用贝叶斯方法估计杉木人工林树高生长模型，为杉木人工林树高生长模型估计提供了一种新思路。Lu等[14]运用贝叶斯模型平均法研究了杉木竞争、立地指数和气候因子对树木死亡率的影响，为杉木人工林经营管理提供了重要依据。贝叶斯方法在森林火灾方面也做了相关研究。Thomas等[15]考虑到法国地中海的气候和环境以及人为因素等影响条件，利用贝叶斯模型预测当地森林火灾的发生情况，研究提高了预测精度，进而减少了经济损失。刘臣园等[16]通过贝叶斯分类器分析林火监控图像，提高了林火识别方法的准确性。高学攀等[17]基于贝叶斯网络分析气象、地理、植被等对林火发生概率进行了预测，综合历史数据，设计并建立了贝叶斯网络推理系统。

本次研究的实验区是贵州省黔南布依族苗族自治州，研究数据包括发生森林火灾发生数据和火险天气下的气象因子数据，采用模拟发生森林火灾次数的模型，包括ZINB（Zero-inflated negative binomial）、NB（Negative binomial）两种，其中ZINB是指零膨胀负二项模型，NB是指负二项回归模型，结合贝叶斯理论，研究分析发生森林火灾次数与气象因子之间的关系以及评价模型的不确定性，可有效保证研究结果的准确性和可靠性。本研究为该区域森林火灾发生预测提供重要的参考依据，也为森林火灾发生预测模型的构建提供可行性思路。

1 研究区概况与数据来源

1.1 研究区概况

本研究的实验区位于贵州省中南部的黔南布依族苗族自治州（下文简称黔南州），地理位置为106°12′～108°18′E，25°04′～27°29′N，辖都匀市、福泉市、瓮安市、龙里县、贵定县、惠水县、长顺县、罗甸县、平塘县、独山县、荔波县和三都水族自治县12县（市），面积26 197 km2。地势东南部略低，西北部较高，地貌类型呈现多样性，但大多以山地为主。黔南州属于贵州省森林火灾的高发地区，受特殊的地理位置影响，历来冬旱和春旱相连，气候非常干旱且炎热，林火火源复杂，气候长期处于高火险等级。研究区是贵州省所有县市中进入防火期最早且结束防火期最晚的地区，在全省范围内它的防火期持续时间最长。黔南州每年1月至4月为重点森林防火期，其余时期为一般防火期。黔南州气候属中亚热带季风湿润区，其特点是季风气候明显，日照较少，湿度偏大，常年平均气温维持在13.2～19.5℃之间。黔南州近几十年来森林火灾日趋严重，这是由多种因素作用形成的，综合反映了多参数以及海量复杂信息。

1.2 数据来源

本文数据由黔南州林业局、黔南州气象局、科技条件基础平台建设项目国家林业和草原科学数据共享中心提供。本研究数据调查时间为1996—2007年和2012—2017年的1月至3月，实验区数据调查范围包括黔南州的12个县（市），数据内容主要包括火险天气时段各县（市）气象数据以及历史森林火灾数据，其中林火数据包括各县市林火面积和各县（市）林火发生次数。

根据查阅相关文献信息资料，本次研究涉及的气象因子包括：月最高温度（Tmax）、月平均温度（Tm）、月平均相对湿度（Hm）、月最小相对湿度（Hmin）、月平均风速（Sm）、月最大风速（Smax）、月降水量（Ra）、月蒸发量（Ev）。本次研究选取的样本中，数据总计620个，在该区域内防火期的各气象因子统计情况见表1。

表1 研究区域在防火期内各气象因子的统计值Table 1 Statistics of meteorological factors during fire prevention period

1.3 数据分析

森林火灾发生的次数分布见图1。由图1可知，完全没有发生火灾的月份多达197个月，频数分布呈现极度正偏态，说明模型数据中存在大量的零数据，分析可知该数据的结构比较离散，为零过度膨胀的状态。

图1 森林火灾发生次数分布Fig.1 Histogram of the distribution of forest fires occurrence

2 研究方法

2.1 数据多重共线性分析

本文研究模型构建前首先对研究中涉及的所有变量进行多重共线性分析，从而保证变量之间不存在共线性相关，保证模型分析的准确性和可靠性。共线性检验指标的选择有很多，方差膨胀因子（VIF,Variance inflation factor）是本研究选取的检验指标。VIF因子的取值范围说明了自变量与其他自变量间存在共线性的可能性大小，VIF的值越高，说明各变量间存在共线性的可能性越大。当VIF的值大于10时，便判定变量之间存在多重共线性。通过分析，本研究中气象因子的VIF取值最大值为3.5，不存在多重共线性。

2.2 贝叶斯理论分析

贝叶斯基础理论由分析数据、构建概率模型、假设先验信息分布、假设效应函数以及得出决策分析五部分内容组成。贝叶斯理论的推断思路包括四个步骤：第一，将先验信息与样本信息结合起来，其中先验信息是未知的，它来自于主观信念和历史文献资料，是统计推断时不可或缺的一个要素。在林业领域里，上一期调查数据的分析结果常常被作为下一次分析检验调查的先验信息。第二，推测后验信息，推测的依据是贝叶斯定理。第三，推测未知参数[18-19]。本研究将森林发生火灾的次数用向量y=(y1,y2,y3,…)表示，参数用向量φ=(φ1,φ2,φ3,…)表示，计算公式如下：

式中：p为密度函数或者概率分布函数。参数φ通常会利用最大似然估计法或是最小二乘法来估算，而在贝叶斯法中，参数φ的不确定性是通过概率分布来描述的。参数φ的条件概率分布公式如下：

参数的后验分布在使用贝叶斯方法进行模型分析时通常用p(φ|y)表示。在利用贝叶斯法分析问题的过程中，必须要进行先验分布的正确选择[9]。先验分布有两种，分别是有信息分布和无信息分布。通常情况下，无信息分布使用较多，表示数据的分布呈现正态分布，而且均值大小是0，方差足够大；有信息分布主要是基于研究者的主观思想以及发表过的文献资料[12]。

本次研究的森林发生火灾次数的模型中，所采用的参数先验分布是无信息分布，即N(0,1 000)。本研究采用SAS软件的proc mcmc模块对贝叶斯参数进行估计，并设置5万次迭代，1万次退火，保证后验概率值的平稳性。

2.3 模型的选择

本研究通过分析和比较，选择零膨胀负二项模型和负二项模型的其中一种作为黔南州森林火灾发生的模型，模型建立后基于数据进行了偏差分析。

1）负二项模型

负二项分布也被定义为Γ-Poisson分布[20]。当θ→1时，负二项分布退化成为Poisson分布，此时事件发生是随机的。负二项分布的方差偏大，它个体出现的几率一部分要小一些，另一部分的几率要大一些，即负二项分布中的参数λ不是固定而是变化且有规律的，这也是它的个体出现概率不相等的原因[21-22]。

NB的概率密度函数中θ为离散参数，μ为均值，负二项分布的方差为μ+(1/θ)μ2，负二项分布的方差比均值大。均值μ仍然可以加入一些协变量估计出来，即μ=exp(xiTβ),i=1,2,...,n。Γ(·)是Gamma函 数，那么：

如上得到了负二项方程的对数似然函数，进而能求出参数的估计值。

由负二项分布可知，E(Y)=μ+(1/θ)μ2。

其中 (yi,xiT)表示第i组数据，xiT=(xi1,xi2,...,xip)∈Rp是已知非随机设计点列，β=(β1,β2,...,βp)T为未知参数。

2）零膨胀负二项模型

零膨胀模型是以零值来分段建立一个混合的概率分布，它把观察的数据设置为结构零部分和离散部分，并且将两部分内容分别设定为模型，用于处理事件发生数中过多零的问题[23]。所以零膨胀模型中的计数随机变量来自于两个部分：结构零部分和离散分布部分[24]。影响该模型零膨胀部分概率通常来源于各种条件或因素水平的组合，当起火概率很小或不具备起火条件时，比如雨下得很大而温度很低的气象条件下通常很难会发生火灾，而零膨胀部分在这种情况下发生作用的几率会很高。

ZINB的概率函数有：

对于参数μi和pi分别用ln和logit连接函数，即其中，和分别是影响μi和pi的设计阵，β=(1,β1,β2,β3,…,βm1)和γ=(1,γ1,γ2,γ3,…,γm1)分别是未知的参数向量，则

则ZINB分布的期望、方差为：

当1/θ→0时，ZINB模型就退化为ZIP模型。从式（6）可知，E(Y)μ/θ用来描述观测数据中的过离散现象。ZINB回归模型是NB部分引入解释变量后得到的，ZINB的对数似然方程为：

2.4 模型的评价方法

本研究采用偏差信息准则DIC(Deviance information criterion)统计量来进行拟合评价指标，DIC值越小，说明模型拟合的效果越好。

式中：Dbar=Eθ[-2log(p(y/θ))]评价模型拟合的优劣性；pD指参数的有效个数。为了验证贝叶斯模型，对贝叶斯模型和传统回归模型进行了比较，并通过均方根误差（RMSE）进行选择，RMSE越小说明模型表现越好。

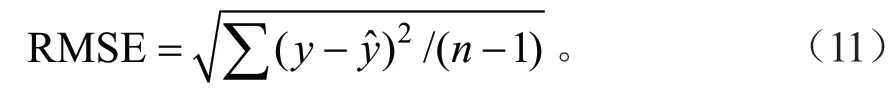
3 结果与分析

3.1 模型的比较

通过参数平整性分析，发现模型中持续存在的气象因子有3个，分别是月最大风速、月蒸发量、月最小相对湿度。根据贝叶斯方法，两类模型的评价指标如表2所示，两种模型中ZINB模型的拟合效果更好。在该模型中，月蒸发量和月最小相对湿度均小于0，则森林发生火灾的次数与二者呈反比关系；反之，若月最大风速的估计值大于0，则森林发生火灾的次数与最大风呈正比关系。由表2中的DIC值可以看出，ZINB的DIC值为2 982.084，而NB的DIC值为3 007.279，DIC值降低了0.8%，结合利用贝叶斯理论，通过比较可发现，ZINB模型拟合的效果比NB模型效果理想。

表2 NB模型和ZINB模型的参数估计及统计检验Table 2 Parameter estimations and statistical test for NB model and ZINB model

基于ZINB模型，通过传统回归方法进行分析并与贝叶斯法进行了比较，结果见表3。由表3可知，传统法的RMSE比贝叶斯法大，由此说明传统模型比贝叶斯模型精度低。

3.2 模型评价

为了分析参数的不确定性，对各项参数都进行了迭代计算，以参数Smax的迭代过程（图2）为例，当去除1万次退火后，该参数的估计值变化比较平稳，无明显波动；在参数Smax的后验图中，参数的估计值变化情况服从正态分布，具有一定的不确定性。

图2 火灾预测模型的参数后验分布Fig.2 Posterior density curves of forest fire occurrence model

4 结论与讨论

4.1 讨 论

本研究基于两种计数模型（负二项和零膨胀负二项模型），采用贝叶斯方法构建森林火灾发生数和气象因子的关系模型。火灾预测模型建立时，发现样本数据中有很多“0”，且离散化现象非常严重，故构建模型前对研究中涉及的所有变量进行多变量共线性分析，此外，对参数进行平整性分析，即对模型的参数迭代计算，发现模型中保留的气象因子有3个，分别是月最大风速、月蒸发量、月最小相对湿度。研究发现空气湿度和蒸发量是影响森林火灾的两个关键因子，气候干燥程度反映一个地区大气水分收支状况，体现了区域水量平衡的变化，空气湿度和月蒸发量都是评价气候干燥程度的一个重要指标。空气湿度是用来表示空气干湿程度和空气中含水量的物理量，所以最小相对湿度的大小关系到可燃物着火和火势蔓延的程度[25-26]。通过研究发现，月最小相对湿度越大，森林火灾发生数的概率就越低。相反，月最小相对湿度越小，当地发生森林火灾的概率就越高。如连续无降水日天数越长，而月蒸发量越大时，空气中的相对湿度就会越小，森林可燃物就越干燥，森林火灾发生的概率就越大。月最大风速也是影响森林火灾的关键因子，风速的大小决定了可燃物水分蒸发的快慢，风速越大可燃物干燥的速率越大，使可燃物变得非常易燃。风速增大的同时还补充了新的氧气，大大增加了可燃物的燃烧条件。通过研究发现，月最大风速越大，森林火灾发生数的概率就越高。相反，月最大风速越小，当地发生森林火灾的概率就越低。

由于不同月份森林火灾发生次数不同，并不是每个月都发生火灾，样本数据中存在着大量的“0”数据，也就是火灾发生次数分布中将会出现多零次（Zero-inflated）现象。如果零次发生的个数超过负二项分布所允许的极限，就可能导致过离散问题，再继续建模研究就很可能会偏离实际。因此，零膨胀模型是拟合零过多数据较好的一类模型。研究表明，两种模型中ZINB模型的拟合效果最好。因为NB模型在建模过程中不能模拟零数据，导致信息不完整，影响预测效果，而ZINB在建模过程中能够对零数据进行分析。此外，研究表明贝叶斯方法可提高预测结果的稳定性和可靠性。

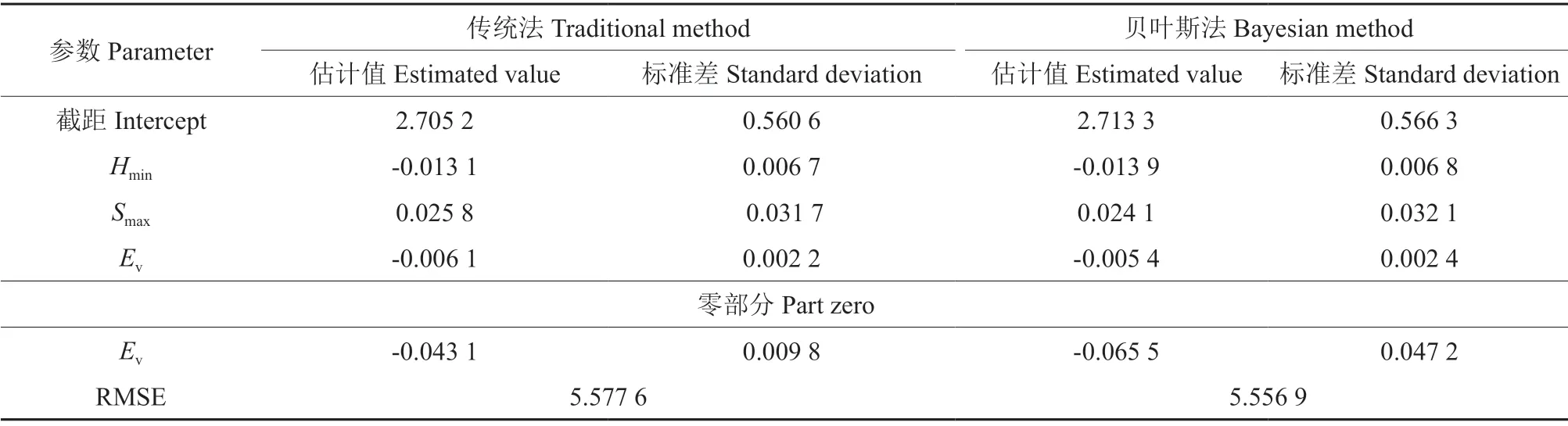
表3 基于传统法和贝叶斯法的ZINB模型参数估计及模型评价Table 3 Parameter estimates and model evaluation statistics of ZINB model using traditional and Bayesian methods

通过本研究结果对比分析，传统方法的RMSE值大于贝叶斯方法，认为贝叶斯推断法优于传统推断法，具体表现为：传统推断法仅仅基于样本信息［12-13］，未知参数的估计值是固定值，不发生变化［13,23］，数据服从高斯分布［24,27］；而贝叶斯推断法基于先验信息和样本信息，并且前者是必不可少的信息，其来源通常是历史文献作者的主观思想，参数和样本数据可以发生变化，而且它的变化是随机的且对模型和参数没有限制。综上所述，采用贝叶斯法估计森林火灾发生模型，可保证预测效果的稳定性和可靠性，对于不确定性的评价比较准确，评价的依据是后验分布。

下一步可以更加深入研究贝叶斯方法在森林火灾模型中的应用，后续可以考虑可燃物等变量的因素，增加先验分布的精确度，通过分层的方法来提高贝叶斯模型的精度，从而使得森林火灾预测模型的模拟效果更加精确。另一方面也要承认可能同时存在几种符合森林火灾发生情况的不同模型，而且这几个模型在不同的地形、不同的森林类型表现出不同的拟合水平。因此，所拟合出来的森林火灾发生在模型结构方面也存在着一定的不确定性。虽然通过模型参数的不确定性反映出了模型的不确定性，但对于模型结构的不确定性还未解决。那么，该如何结合不同模型的预测表现，如何分析评价森林火灾发生模型结构的不确定性很值得下一步继续研究。

4.2 结 论

本研究以贵州黔南布依族苗族自治州为研究区域，采用零膨胀负二项和负二项回归两种模型模拟森林火灾发生次数。研究发现，零膨胀负二项模型由于建模过程中能够很好地对火灾零次发生数据进行分析拟合，模拟精度要比负二项模型好。其次，森林火灾发生数随着月最小相对湿度的增大而减小，与月最大风速的增长而增加。基于零膨胀负二项模型，研究发现贝叶斯法在拟合火灾发生数方面比传统法精度高。利用贝叶斯法估计森林火灾发生模型能够很好地提高模型预测可靠性，并且根据参数的分布评价森林火灾发生数的不确定性，最终得到以下模型：