基于问题导向的极大线性无关组教学设计研究

【摘要】以线性代数中的极大线性无关组教学为例，通过实际生活中的例子引入，从提出问题、分析问题到解决问题的全过程，展示了对极大线性无关组的概念、性质和求法的问题导向型教学设计案例，让学生充分体会到线性代数在实际生活中的应用.

【关键词】线性代数;极大线性无关组;教学设计;问题导向

1 引 言

问题导向型教学设计是最直接有效的一种教学设计模型，在现实的教学操作中也广为教学设计者们喜爱，它清楚明白地展示了如何运用知识解决实际问题，对于像线性代数这种抽象的理论十分适用且效果显著.本节教学设计以培养学生的核心素养为总目标和指导思想，激发和培养学生的数学素养，以情境式教学和探究式教学为主要形式，注重与学生的生活实际相结合.以当下热门的社会现象为课前引入，激发学生的兴趣，使他们积极探讨问题背后的数学知识，最终解决实际问题.从生活中来作开头，到生活中去作结尾，让学生充分体会线性代数在实际生活中的应用.

2 极大线性无关组的教学背景

2.1 教材分析

教育部高等学校大学数学课程教学指导委员会颁布的《大学数学课程教学基本要求》对本节内容的要求为：了解向量组的极大线性无关组的概念，会求向量组的极大线性无关组.

本节内容位于线性方程组这一章中，向量组的秩这一小节.向量是线性代数的重要内容，对研究线性代数的中心内容——线性方程组起到了至关重要的作用，而充分理解向量组的极大线性无关组这一概念，才能理解向量组的本质和内部关系，同时为后面理解线性方程组解的结构和掌握线性方程组的求解方法打下基础.另外，极大线性无关组的常用求法是利用第二章矩阵的初等变换，因此，本节内容对于线性代数前后知识的关联、融合十分重要，学好本节知识有利于学生将全部线性代数内容形成一个体系.

2.2 学情分析

学生在学习本节知识之前，已经学习了向量组的线性相关性和矩阵的初等变换，在线性无关的基础上，本节内容的关键就是理解“极大”这两个字的含义，另外，极大线性无关组的不唯一性是一个难点，这对理解极大线性无关组的本质和作用将是一个障碍.这一障碍是通过引入具体的向量组例子和导入环节中导入现实生活中实际的例子来解决的，从而帮助学生理解不唯一性这一难点.

2.3 教学目标

1.知识与技能：理解极大线性无关组的概念，了解极大线性无关组的性质和作用;掌握利用矩阵的初等变换求向量组极大线性无关组的方法.

2.过程与方法：通过观看图片和视频，让学生增强从生活中发现问题、提出问题的意识;通过现实生活中的例子和极大线性无关组的数学概念，使学生学会理论联系实际的方法;通过抛弃“多余”向量，让学生体验数学中化繁为简的思想方法;通过问题从引入到分析再到解决的全过程，教会学生从实际问题中建立数学模型，并应用数学理论知识解决问题的本领.

3.情感、态度与价值观：通过参与发现问题到最终解决问题的全过程，让学生充分领略数学的魅力和价值;通过引导学生对极大线性无关组概念的理解和性质的推导，培养学生主动思考、积极探究、不怕困难的精神和态度;通过对热门的社会现象的思考，培养学生的创新意识和综合素养.

以上三种目标不是独立存在的，是在教学过程的每一步中有机地统一在一起，相辅相成的.

2.4 教学重、难点

教学重点：用初等变换求极大线性无关组.

教学难点：对极大线性无关组不唯一性的理解，对极大线性无关组的性质和作用的理解.

2.5 教学策略

本课程通过对社会现象的讨论引入实际案例，为解决问题而开启数学理论知识的学习.课程在设计中注重：1.从学生的生活体验出发.学生是体验的主体，生活是体验的情境.2.以问题为中心，带着问题走进教材，靠着解决问题走进生活.以情境式和探究式为主要的学习方式贯串始终.

2.6 教学手段

在引入问题环节，教师通过展示图片和视频增加直观性和趣味性;再通过提问引发学生思考;通过PPT来展示定义和例题;通过板书的形式来展示性质的推导和具体计算，这样一步步的推导体现了数学的严谨性.

3 极大线性无关组的具体教学过程

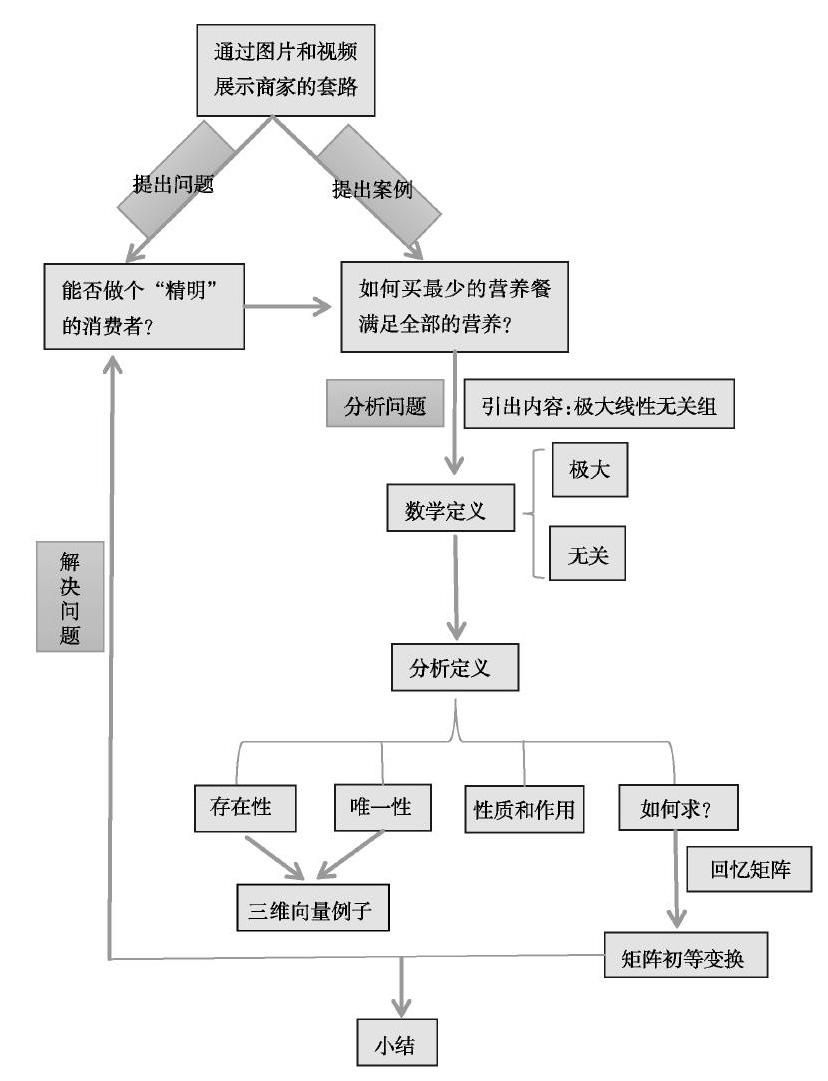
完整的教学过程可简单地用流程图表示如下：

教学过程具体可分为如下的步骤：

1.导入环节

描述现象——首先观看一段网络热门搞笑视频：生活中，商家的促销手段可谓五花八门，令人眼花缭乱，尤其是近些年来电商的蓬勃发展，你一定也经历过各种购物狂欢节中烦冗复杂的规则和套路，有网友吐槽“领到了购物津贴你就领到了数学试卷”.

提出问题——面对“精明”的商家，我们怎样才能不被套进去，做一个“精明”的消费者？

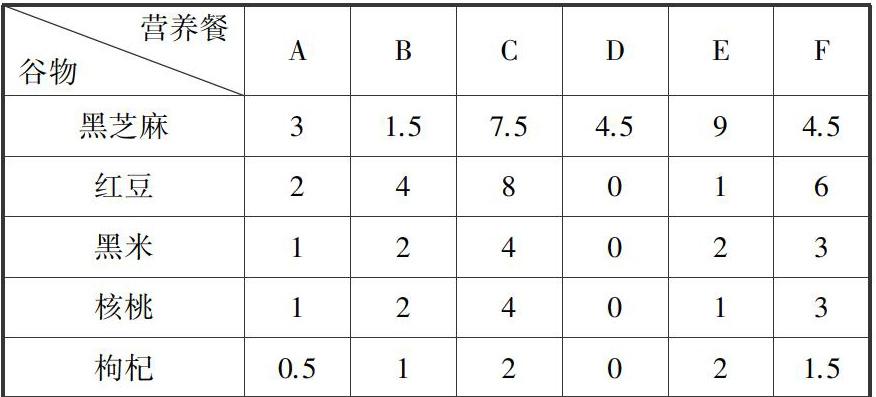
建立模型——某商家打算用5种成分来制造多种谷物营养餐，下表列出了6种营养餐A，B，C，D，E，F每份所需各成分的量（以每10克为单位）.

顾客要想得到全部的营养，当然购买全部的6种营养餐即可，然而是否可以少花些钱，只买其中的一部分，就能搭配出全部的营养餐呢？为了获得全部的营养，需要购买最少的营养餐种类是哪几个？

引出主题——向量组的极大线性无关组.

2.讲授环节

（1）为解决问题，给出线性代数中极大线性无关组的定义，并对定义进行分析.

（2）对于极大线性无关组，我们要研究的问题分为四部分：存在性、唯一性、性质和作用，如何求？对这四部分一一展开讨论.具体来说，按照定义通过对向量组α1=1

0线性相关性的探讨，得出结论——非零向量组的极大线性无关组一定存在，若整个向量组线性相关，则极大线性无关组不唯一，这同时解决了存在性和唯一性两个问题.通过对定义的分析，可以推导出极大线性无关组的性质和作用——与原向量组等价，因而在讨论时可以代替原向量组，不必考虑多余的向量，使问题简化.通过向量与矩阵的联系，启发和引导学生发现极大线性无关组的常用求法——转化为矩阵问题，利用矩阵的初等变换解决问题.

3.巩固环节

利用刚得到的极大线性无关组的求法，对导入环节中的案例进行推导计算，6种营养餐可看作6个向量，求出这6个向量组成的向量组的极大线性无关组，它可以表示所有的向量，因而可以配出全部的营养餐，满足全部的营养成分，问题得到解决.

4.小結环节

在社会现象中思考，经历发现问题、提出问题、分析问题的过程，最终利用数学知识解决问题.

相关的知识点有：极大线性无关组的定义、存在性、唯一性、性质、作用、求法.其中的重点是极大线性无关组的求法.难点是对极大线性无关组不唯一的理解及对性质和作用的理解.

4 教学反思

线性代数中高维的向量是纯理论的概念，没有几何表示，因而极具抽象性.本节教学设计通过实际生活中大家都会遇到的典型例子，让学生对线性代数这一抽象的概念有一个具体的认识.网络上热门的搞笑视频在课程一开始就抓住了学生的眼球，增强了课堂的趣味性，也容易让学生产生共鸣，从而使学生自然而然地提出问题，引发思考.

极大线性无关组是向量的重要概念，相关的计算也是关于向量的重要运算.矩阵的初等变换贯串整个线性代数的始终，更是极其重要的，也是学生必须要熟练掌握的一种计算方法，在教学中要通过实例重点讲解和练习它.对于极大线性无关组的不唯一性这一难点，通过三维向量的简单实例予以解释说明.

从生活中来到生活中去的完整过程，展现了数学建模的思想和发现问题、分析问题到解决问题的全过程，有助于培养学生的自主思考意识，提高学生的核心素养.

【参考文献】

[1]马荣.线性代数[M].南京：南京大学出版社，2018.

[2]赵树嫄.线性代数：第4版[M].北京：中国人民大学出版社，2013.

[3]付苗苗.基于案例的线性代数课堂教学研究[J].科技经济导刊，2019（21）：147.