用双椭圆方法确定反射点位置

李启成，苑树鹏，郑新娟 ，席桂梅，贺翔，吴奎，徐伊豪

1)辽宁工程技术大学矿业学院，辽宁阜新，123000；2)朝阳工程技术学校，辽宁朝阳，122000；3)朝阳师范专科学校，辽宁朝阳，122000

内容提要: 在反射波地震勘探中使用动校正确定反射点位置用到很多假设，如勘探深度要远远大于炮检距；假定倾斜反射界面的反射点与水平反射界面反射点都位于炮检距的中点；近似认为倾斜反射界面的动校正量等于水平反射界面的动校正量；假定反射面倾角固定且较小等，上述假设一定会造成勘探误差。由于反射点位置和反射面倾角未知，所以理论上无法唯一地确定反射点位置。如果反射波传播的介质的波速一定，从炮点发出的地震波，经反射点后，在接收点被接收，其可能的反射点是椭圆的一部分，但还不能唯一确定反射点；再取炮点和另外一个接收点，其可能的反射点是另外一个椭圆的一部分。如果假定反射面是平面，可以是水平面，也可以是有固定倾角的倾斜平面，该平面在地震波射线平面内是一条直线，该直线一定是两椭圆的公切线。把两椭圆方程和切线方程联立，就可以求解出公切点位置，公切点位置就是反射点位置，这就是用双椭圆确定反射点位置的方法。通过建立模型对勘探方法进行了检验，证实了用双椭圆方法确定反射点位置的有效性。双椭圆方法有一个重要的副产品，就是在确定反射面位置的同时计算出反射面的视倾角。

动校正技术在地震勘探中被广泛采用(谢俊法等, 2017; 李江, 2018; 范涛, 2019; Mohammad et al., 2019)。但用反射波确定反射点的动校正会导致许多误差： ①勘探深度要求远远大于炮检距(闫靓, 2007；陆基孟等, 2011; 李洪强, 2014; Sedek et al., 2017)，如果在浅层勘探中一定会产生不可忽略的误差；②假定倾斜反射界面的反射点与水平反射界面反射点都位于炮检距的中点(Larner et al., 2007; 陆基孟等, 2011; 张博, 2012)，实质是假定了反射界面倾角较小，在倾角较大情况下，势必产生较大误差；③近似认为倾斜反射界面的动校正量等于水平反射界面的动校正量(陆基孟等, 2011; 曾忠玉, 2013; 张志明等, 2016)，这也是产生误差的原因；④动校正后经偏移归位确定反射面也会产生误差(Jervis et al., 1996; Docherty et al., 1997; 陆基孟等, 2011; 撒利明等，2015; 芦俊等, 2018; 李广超, 2019; 郑佳梁, 2020)；⑤计算叠加速度过程中采用速度步长不同也会产生误差。基于目前用动校正确定反射点位置误差较大的问题，提出用双椭圆方法确定反射点法线深度方法。

1 用双椭圆确定反射点位置的原理

在反射波勘探中，在射线平面内建立如图1坐标，从炮点x0激发的地震波，在反射点O反射后在x1点被接收，地震波的走时为t1，介质1中的波速为v。地震射线从发射，经过反射，最后被接收，所走的路径长度为vt1，可能的反射面是以x0和x1为焦点，以vt1为定长的椭圆面，该椭圆设为椭圆1。当然，该椭圆面应该位于地面以下，也就是表示反射面位置的纵坐标为负值。再设从炮点x0激发的地震波，在另外一个反射点反射后在x2被接收，可能的反射面在图1中的椭圆2上。设反射面是一个有固定倾角的平面，这样的假设符合目前地震勘探对反射面的认识。椭圆1和椭圆2上的反射点一定同时与该反射面相切，所以反射面在射线平面内，一定位于两椭圆的公切线上。确定地面以下的两个公切点，就是实际的反射点。

如图1，为以后讨论方便，我们重新假设。令x0为炮点，从x0点发出的地震波经O点反射，到达xn被接收，地震波走时为tn，n=1,2,...N-1.n为记录点序号，N为记录点最大序号。设有一个反射面存在，反射面以上为介质1，其波速为V，反射面以下为介质2。地震射线与反射面的交点不是唯一确定的，反射面是分别以x0和xn为焦点，以ox0+oxn为定长的椭圆面，可能的反射点在椭圆上。如图1建立坐标系，水平坐标建立在共炮点勘探的纵测线上，炮点x0与接收点xn连线中点P为坐标原点，纵坐标y′表示在射线平面内反射面的纵坐标。可能反射面的椭圆长轴为an，短轴为bn，焦距为cn。

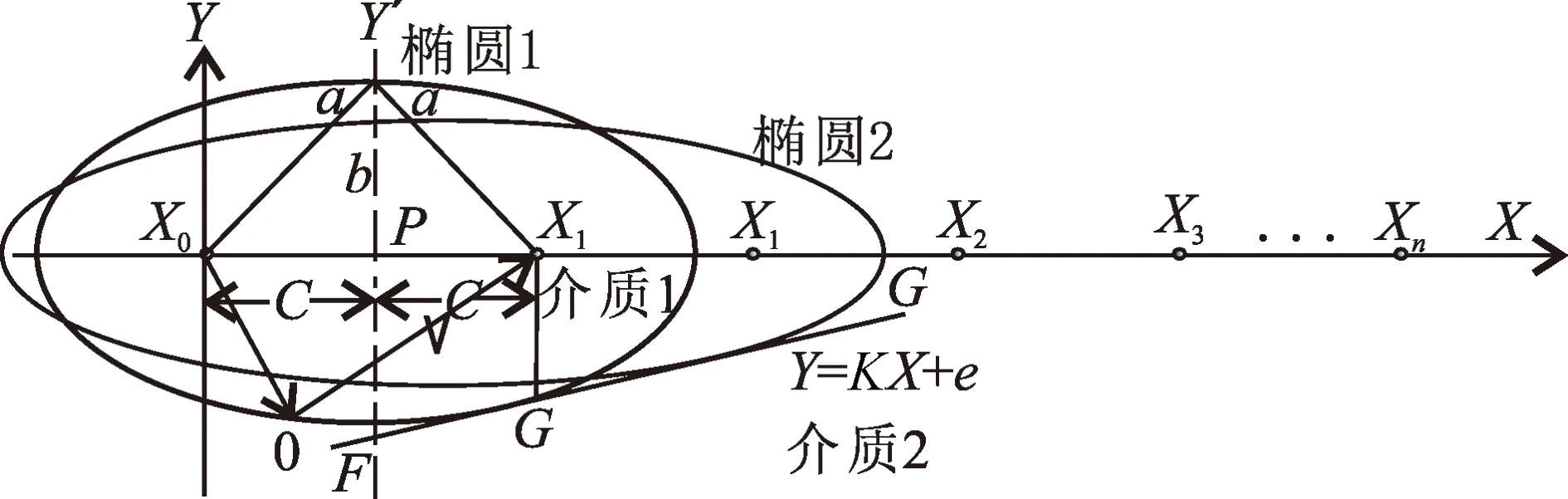
图1 双椭圆确定反射点Fig. 1 The determination of reflective point with double elliptical method

椭圆方程为：

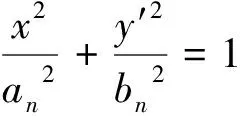
把y′轴平移到x0，令为y轴，则椭圆方程变成：

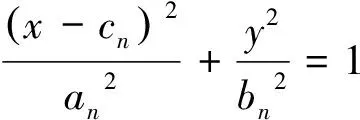
(1)

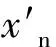
(2)

其中字母含义与公式(1)类似。

设反射面在两次的反射点之间是一个连续的有固定倾角的斜面，设其在地震波发现平面内的直线方程为：

y=kx+e

(3)

其中k为直线斜率，e为截距。

该直线与两椭圆分别有一个交点，也就是该直线在两椭圆的公切线上。把公式(3)带入公式(1)得：

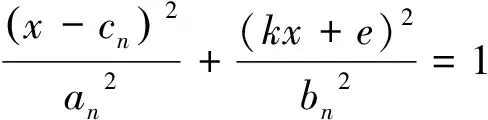
(4)

(5)

方程(3)代表的直线与方程(4)代表的椭圆相切，只有一个交点，一元二次方程(5)是根的判别式，其值应该等于0，所以：

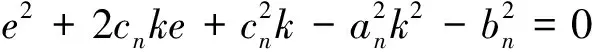
(6)

解方程(6)，得到：

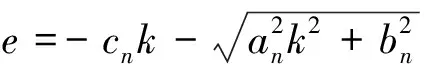
(7)

公式(7)中跟号前取负值原因是反射切面在地下，其截距为负值。

同理，由公式(2)得：

(8)

把k值定在0到tg89°和-tg89°到0之间变化，k的步长为0.0001，对方程(8)进行迭代运算，取得方程中的m最小值对应的k就是反射面的斜率。在把k值带入公式(7)，得到反射面的截距e。

解方程(5)，得到第一个反射点的水平坐标x0n，把值带入方程(3)，得到对应的纵坐标y0n。

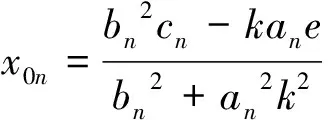
(9)

(10)

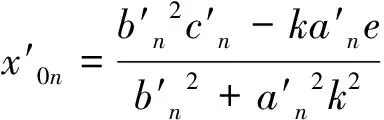
(11)

(12)

据此，提出一种用双椭圆确定反射点准确位置的方法，具体步骤如下：

步骤1：建立纵测线，确定炮点和接收点的位置坐标，在射线平面内，以测线为水平坐标轴，以深度为纵坐标，炮点为坐标原点建立坐标系；

步骤2：激发地震波，记录地震波到时，得到反射波的时距曲线；

步骤3：从第一个接收点开始，取相邻两接收点x1和x2记录数据带入方程(8)，把反射面斜率K值定在0到tg89°和-tg89°到0之间变化，k的步长为0.0001，对方程(8)进行迭代运算，取得方程中的m最小值对应的k就是反射面的斜率。在把k值带入公式(7)，得到反射面的截距e；用公式(9)-(12)计算两个反射点的位置坐标(x01，y01)，(x02，y02)；同理取相邻两接收点x3和x4....,xN-1和xN代入相关公式计算，最后得到反射点坐标序列q=(x01,y01),(x02,y02)，...，(xN,yN)；

步骤4：用坐标序列q绘制反射面位置坐标曲线。

2 双椭圆方法验证

下面结合具体实施实例对用双椭圆方法确定反射点准确位置的方法进行说明，具体流程如下：

步骤1：建立纵测线，确定炮点和接收点的位置坐标，在射线平面内，以测线为水平坐标轴，以深度为纵坐标，炮点为坐标原点建立坐标系；

步骤2：激发地震波，记录地震波到时，得到反射波的时距曲线，如图2所示；

上述地震数据获得过程是：假定如图3的反射面，通过理论计算得到地震波走时随位置坐标的变化关系。图3中反射面倾角φ=30°，首先以O点为炮点，由O到D点取一系列接收点，O点的法线深度取h=300 m，OD之间距离取300 m，每隔10 m取一个记录点，得到图2中的上行波记录；在以D点为炮点，由D到O取相同的记录点记录，D点的法线深度为h=150 m，得到图2中下行波的地震记录。取双向测量的目的是增加数据量以减小误差。

图2 反射波地震记录Fig. 2 The seismic records of reflective wave

获得图3中反射波走时的计算方程为：

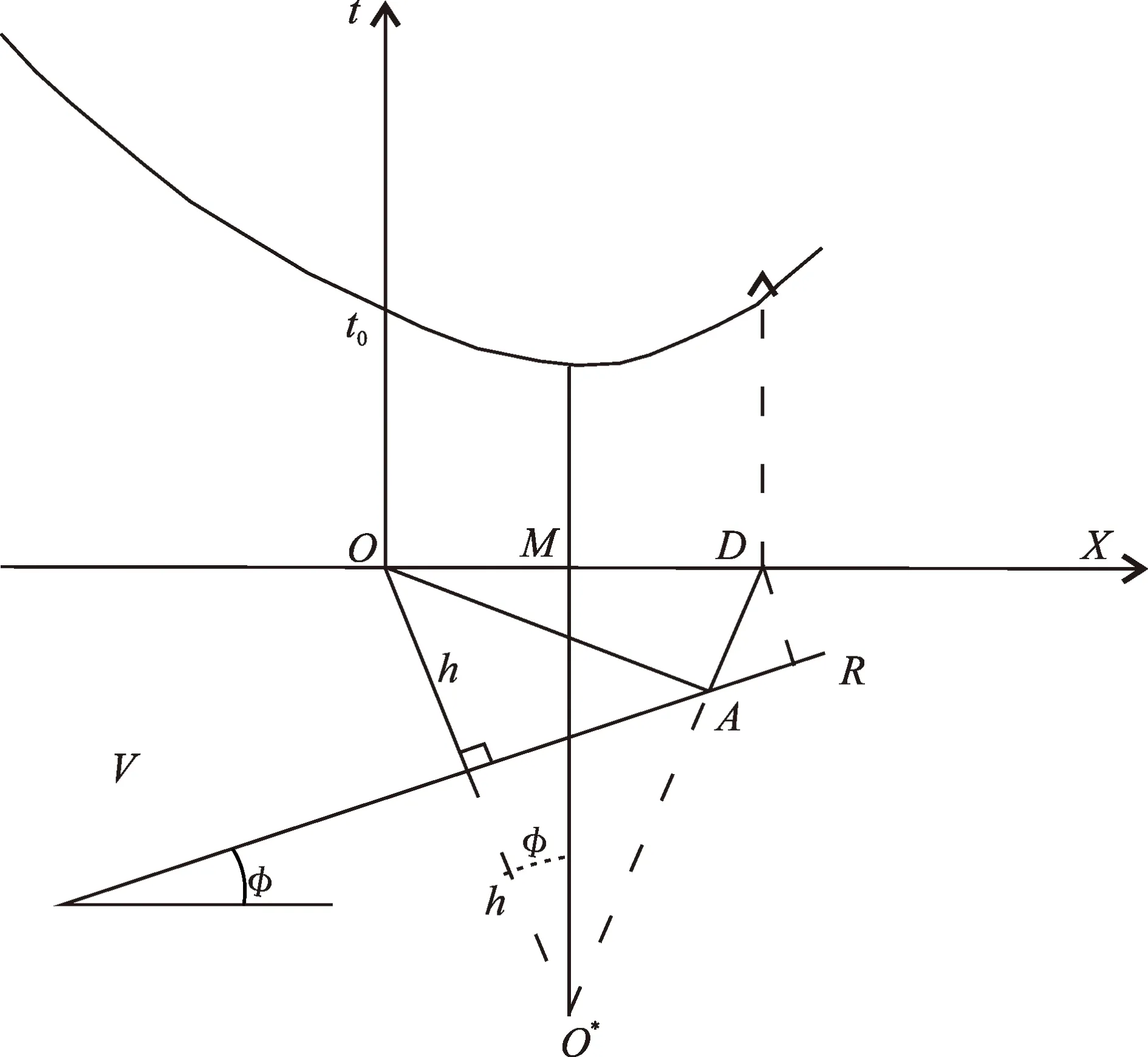
图3 获取地震记录用的反射面Fig. 3 The reflective surface that is used to get seismic records

(13)

公式(13)中h为法线深度，x为检波距，其他字母含义同文中定义。

步骤3：从第一个接收点开始，取相邻两接收点x1和x2记录数据带入方程(8)，把反射面斜率k值定在0到tg89°和-tg89°到0之间变化，k的步长为0.0001，对方程(8)进行迭代运算，取得方程中的m最小值对应的k就是反射面的斜率。在把k值带入公式(7)，得到反射面的截距e；用公式(9)-(12)计算两个反射点的位置坐标(x01，y01)，(x02，y02)；同理取相邻两接收点x3和x4....,xN-1和xN代入相关公式计算，最后得到坐标序列q=(x01,y01),(x02,y02)，...，(xN,yN)；

步骤4：用坐标序列q绘制反射面位置坐标曲线，如图4。

图4 勘探结果Fig. 4 The exploration result

由于地震勘探数据是由理论模型计算得到，很方便对勘探结果进行检验。我们理论模型的反射面倾角为30°，其斜率为0.577，我们勘探得到的反射面斜率为0.580，其它法线深度数据也与预设的基本吻合。

3 讨论

在地震反射波勘探中，从理论上讲，由于反射点位置和反射面倾角未知，如果仅仅已知地震射线走时、炮检距和地震波速度，会有无数个反射点满足条件，如果没有其它限定条件无法唯一地确定反射点位置。作为确定反射点位置的动校正做了较多假设，如假定勘探深度要远远大于炮检距；假定倾斜反射界面的反射点与水平反射界面反射点都位于炮检距的中点；近似认为倾斜反射界面的动校正量等于水平反射界面的动校正量；假定反射面连续变化且倾角很小；速度分析过程中也采用了诸多近似，所以用动校正确定反射点位置必然存在较大的系统误差。

如果假定反射波传播的介质的波速一定，从炮点发出的地震波，经反射点后，在接收点被接收，其可能的反射点是椭圆的一部分，但还不能唯一确定反射点；再取炮点和另外一个接收点，其可能的反射点是另外一个椭圆的一部分。如果假定反射面是平面，可以是水平面，也可以是有固定倾角的倾斜平面，该平面在地震波射线平面内是一条直线，该直线一定是两椭圆的公切线。把两椭圆方程和切线方程联立，就可以解出公切点位置，公切点位置就是反射点位置。这就是我们提出的用双椭圆法确定反射点位置的方法。该方法仅仅有一个假设，就是要求两个反射点之间是连续的反射面，该反射面是任意倾角；动校正中也有类似的假设，假定反射面倾角较小。显然，双椭圆方法唯一的假设包含在动校正方法之中，该假设认为两相邻接收点间的反射面是有固定倾角的平面，由于两反射点间距不大，其对应的反射面有固定倾角的可能性很大，也符合目前对沉积地层的普遍认识，其勘探结果误差一定会相对较小。动校正方法仅仅适用于反射面倾角较小的情况，而双椭圆方法适用于任何倾角的反射平面。

在图3中，O点和D点之间距离为300 m。目前动校正技术中假定倾斜反射界面的反射点位于炮检距的中点。如果按照目前动校正技术勘探，图3中所有反射点都应该位于0～300 m的范围内，但按照我们提出的双椭圆方法勘探，所有反射点集中150～370 m的范围内，如图4。显然我们的勘探结果是正确的，因为我们勘探的反射面倾角30°，假设从O点发出的地震射线，在D点被接收，其反射点一定在D点的右侧，只有OD之间的部分接收点对应的反射点在OD之间。这进一步说明认为倾斜反射界面的反射点位于炮检距的中点的假设是存在误差的，并且当倾斜反射界面倾角较大时，误差是不可以忽略的。

在目前动校正地震成像技术中，要涉及很多速度。在进行时深转换时，用到平均速度(潘宏勋等, 2006; 韩复兴等, 2011; Qadrouh et al., 2014)。在进行偏移处理时，用到射线平均速度。进行岩性解释等情况时，要用到层速度(Mulder et al., 2002; 王珊, 2016; Sedek et al., 2017; 郑佳梁, 2020)。在进行动校正处理或用实测时距曲线拟合时，用到叠加速度(Liu, 1997; Chauris et al., 2002; 秦宁等, 2013; Sedek et al., 2017)。在叠加速度的定义为，一排列上各种检波点记录到某个波不同速度的某种平均值。目前射线物理学中成像原理是对多次覆盖系统的观测结果进行动校正，从而确定共反射点的自激自收时间和叠加速度；在此基础上进行时深转换用的速度是平均速度，但勘探中用平均速度会产生较大误差的，因为平均速度的地震射线是垂直地面传播的，而在实际勘探中，地震射线的传播一般不是垂直地面的，而且随着炮检距的变化而变化。并且，动校正得到的速度既不是平均速度，也不是射线平均速度，而是叠加速度。对于倾斜界面均质介质，叠加速度就是等效速度；对于水平层状介质，叠加速度就是均方根速度。正是由于动校正中的诸多假设导致提出了诸多速度概念，很容易产生理论上的混淆和实践中的应用困难。其表现是在多次覆盖地震勘探资料中直接得到的叠加速度，往往需要换算成均方根速度，再用均方根速度获得层速度，最后用层速度计算得到平均速度或射线平均速度等，才能最终得到接收点对应的真深度，步骤多出现较大误差在所难免。用双椭圆法确定反射点位置不涉及叠加速度等概念，仅仅用到射线平均速度，在理论上是清晰的，在实际勘探中不用考虑各种速度的转换，从而减轻了工作量，有较大实用价值。在实际多地层勘探中，只要准确地拾取各地层反射波到时，并进一步确定各地层中不同接收点的射线平均速度，从而达到用双椭圆法勘探的目的。

在双椭圆方法中的公式(3)中的K就是反射面的视倾角，它可以通过计算反射点的过程中确定，是一个重要的副产品，因为地震勘探必须在掌握反射面真倾角或视倾角的基础上才能计算真深度。目前地震勘探中用另外一套独立方法获得反射面视倾角，而双椭圆法在确定反射点同时就可以确定反射面视倾角。

目前用动校正确定反射点位置方法中，为了减小因理论近似产生的误差，采用多次覆盖技术。我们的双椭圆勘探方法，也可以在同一条测线上采用多次覆盖技术，利用倾角确定的反射面对地震波速度进行校正，并克服覆盖次数少所产生的误差问题。

4 结论

通过建立反射面理论模型，计算得到时距曲线。用上述时距曲线数据作为地震勘探记录检验双椭圆方法，结果表明勘探结果与理论模型吻合得非常好，也初步证明了用双椭圆方法确定反射点位置的有效性。在我们的理论推导和模型计算过程中，不同地震射线用到的射线平均速度是相同的，但在实际勘探中，不同地震射线平均速度一般是不同的，对于水平层状介质，一般炮检距越大，射线平均速度也越大。但这并不影响双椭圆方法的适用，只是要求双椭圆中的第一个椭圆和第二个椭圆的射线平均速度不同而已。今后要做的工作是研究射线平均速度，在地震勘探实践中不断采用双椭圆方法，把用双椭圆方法勘探结果与动校正的勘探结果不断比较，使得用双椭圆方法确定反射点位置的理论得到推广应用。