基于灰狼算法的无线网络组播路由优化*

(中国西南电子技术研究所，成都 610036)

0 引 言

组播路由问题实际上就是在给定的网络拓扑下，设定源节点和目的节点，找出包含源和目的节点的一颗组播树，并且组播树满足约束条件(如链路带宽)，使组播树的开销最短[1-2]。相关学者的大量研究已经证明了组播路由问题是一个NPC(Non-deterministic Polynomial Complete)问题，该问题通常无法直接求得最好结果[3]。在前人研究工作中，早期研究人员侧重于寻找组播树的最短路径，提出了一些基于数学的优化方法，例如Lu等人[4]提出了基于最小生成树的动态贪婪算法,通过该算法产生的多播树的性能在合理的范围之内。这些算法基本上只针对一种QoS约束，应用面较窄。国内外学者结合实际问题，常用一些元启发式算法来求解，以得到一个较优的近似解，例如遗传算法(Genetic Algorithm，GA)、粒子群算法(Particle Swarm Optimization，PSO)等。Chakraborty等人[5]采用了差分进化算法解决了无线网络中多通道情况下的最小代价组播树的构造问题。文献[6]提出一种时延敏感网络下的组播路由算法，通过预处理子图的方式降低计算复杂度，并且缩短组播路径的计算时间。文献[7]基于图论方案建模网络拓扑，提出了一种基于局部邻居信息感知的分布式组播路由算法，并通过真实示例分析验证该算法能够取得良好的性能。文献[8]以最小化多个组播树在共享链路上的组播路由时延为目标，提出了一种基于最短路径树的组播路由算法,致力于降低智能电网应用中多条组播消息同时传输的时延。文献[9]提出了一种在满足带宽约束条件下以最小化能量消耗为目标的组播路由算法，减少维护组播路径状态信息的开销，并设计休眠算法关闭未参与组播路由的节点。目前这类进化算法已经成为求解QoS组播路由问题最主要的研究方向。

本文提出了一种基于模拟灰狼群体狩猎行为的启发式算法，即灰狼优化算法(Gray Wolf Optimization，GWO)[10]，该算法将种群中的个体通过适应度进行排序，选出适应度最好的3个个体，所有个体都向着最优的3个灰狼个体方向进化，通过数次迭代，能够获得一个接近最优解的结果。GWO适用性很强，可以应用到很多不同问题上。本文将该算法做了一定改进，以适用于二进制的编码方式。同时，基于一种个体变异的思想，在GWO狩猎策略执行结束后，对所有个体执行变异策略，一定程度上增强了算法的全局搜索性能。仿真结果表明，相比于遗传算法，本文提出的基于灰狼优化算法的组播路由策略能够得到一棵开销更小的组播树;并且遗传算法优化结果波动较大，算法稳定性较差，而本文提出的灰狼优化算法稳定性更强，同时算法的时间复杂度并没有增加，充分说明了本文提出的灰狼优化算法的高效性。

1 系统模型

本文研究由V个节点构建的多跳无线网络，节点集合定义为V={1,2,…,V}，所有连通节点之间链路集合定义为E={1,2,…,E}。该无线网络的拓扑可以视作一个无向带权连通图G=(V,E)，其中e(x,y)∈E表示网络节点x与网络节点y之间的连通链路。网络中的节点均需要维护本节点与一跳邻居节点的链路连通状态，并通告其他网络节点，使得全部网络节点能够实时获得网络拓扑图G=(V,E)的信息。

假设源节点为s，组播目的节点集合为D={d1,d2,…,dJ}∈V-{s}。组播路由问题就是在给定的网络拓扑G=(V,E)下，设定源节点s和目的节点集合D，找出包含源和目的节点的一颗组播树GT=(VT,ET)，其中VT表示组播树的点集合，ET表示组播树的边集合。

对于网络中任意一个节点v∈V，定义节点度Ws(v)为该节点v在源节点s的组播树参与的链路数。在资源受限的情况下，任意节点v∈V需满足如下节点度约束：

(1)

式中：Tv,th表示节点v的节点度门限值。

对于网络中任意一边e(x,y)∈E，定义边的带宽bandwidth(e(x,y))和边的开销cost(e(x,y))两种属性。其中，边的带宽bandwidth(e(x,y))表示该链路e的最大业务承载能力，单位为Mb/s；开销cost(e(x,y))的值为边所连接两个节点之间的距离。任意一条边e(x,y)∈E，所用拓扑为在城际通信拓扑下的实际距离计算公式如下：

cost(e(x,y))=

(2)

Dlon=Rlonx-Rlony,

(3)

Dlat=Rlatx-Rlaty,

(4)

Rlonx=lonx×π/180°,

(5)

Rlony=lony×π/180°,

(6)

Rlatx=latx×π/180°,

(7)

Rlaty=laty×π/180°。

(8)

式中：lonx和latx分别为节点x的经度和纬度，lony和laty分别为节点y的经度和纬度；Rlatx和Rlaty的单位为rad；ER为地球的半径，取值为6 371 km。latx和latx只用于计算e(x,y)的开销，在网络拓扑已知的前提下它是确定的。令源节点s的链路带宽需求门限值为K，该源节点的组播树中任意链路的带宽均需要大于KMb/s，即

min{bandwidth(e(x,y))|e∈ET}≥K。

(9)

综上，求解最小网络开销的组播路由树的问题可建模为在网络拓扑图G=(V,E)中搜索目标组播路由树GT=(VT,ET)，满足源节点s与组播目的节点集合D={d1,d2,…,dJ}中的任意节点在拓扑子图GT=(VT,ET)中均存在连通路径，并使得∑e∈ETcost(e(x,y))的值最小，同时满足节点度约束(1)和链路带宽约束(9)。由于从源节点到多个目的节点之间存在链路耦合性，典型的单播最短路径算法无法直接应用到求解组播树的问题中，因此求解满足上述条件的目标组播路由树GT=(VT,ET)通常具有较高的复杂度。

2 基于灰狼优化算法的组播路由策略

为了降低求解复杂度，本文采用灰狼优化算法求解目标组播路由树GT=(VT,ET)，解决资源受限的组播路由问题。基于灰狼优化算法的组播路由策略流程如图1所示。

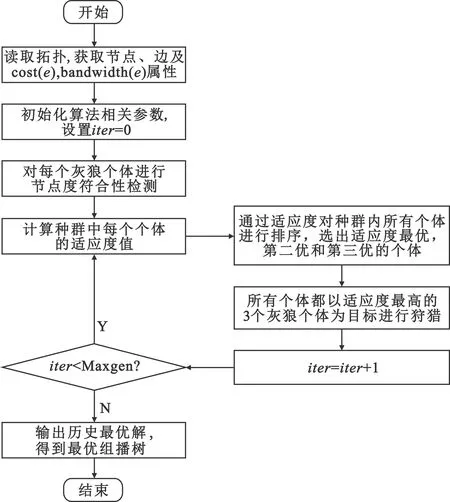
图1 基于灰狼优化算法的组播路由策略流程图

Step1 确定网络参数。通过读取本节点实时维护的链路连通状态信息，确定优化目标和约束条件。

Step2 建立网络拓扑。建立拓扑图G=(V,E)，计算并赋值每条边上的开销cost(e(x,y))，带宽bandwidth(e(x,y))等属性。

Step3 初始化灰狼种群。灰狼种群规模定义为N；初始化第i个个体为二进制向量Li=[l1,l2,…,lM],li∈{0,1}，i=1,2,…,N，其中M的取值等于网络拓扑中的总链路数|E|；算法最大迭代次数为Maxgen；初始化种群历史最优个体为best；其中，N个灰狼个体的所有M个元素均以均匀随机的概率选择0或1。

Step4 灰狼个体的节点度符合性检测。对于任一灰狼个体Li=[l1,l2,…,lM]，根据网络拓扑G=(V,E)，可以得到一个新拓扑GK=(VK,EK)，其中VK∈V,EK∈E。若新拓扑GK=(VK,EK)中存在任意节点v∈VK的节点度Ws(v)=∑y∈VK,y≠v,e(v,y)∈EKe(v,y)大于Tv,th，则将该灰狼个体中从这Tv维非零元素中随机选择Tv-Tv,th维元素重置为零，可以得到一个符合节点度约束的新拓扑GL=(VL,EL)。

Step5 灰狼个体适应值计算。通过适应度函数计算每个灰狼个体的适应度值。个体适应度值表示该灰狼个体对应的满足约束条件的组播路径(即组播生成树)的链路开销之和。如果不满足源节点和任意目的节点连通，将个体适应度置为一个足够大的值。在新拓扑GL=(VL,EL)上，去掉不满足带宽约束的链路后，如果GL=(VL,EL)满足组播源节点到任意目的节点di∈D,i∈{1,2,…,J}均连通(即源到目的地至少有一条可达路径)，则以组播源节点s为起点、EL中各边上的开销为权值，每个目的节点执行1次Dijkstra算法，得到源到任意目的节点的最短路径，用w(s,dj)表示，得到的J条源到目的地的最短路径组合起来，去掉重复边，可以得到一棵组播树GT=(VT,ET)，VT∈V,ET∈E，VT表示组播树中存在的所有节点的集合，ET表示组播树中存在的所有边的集合。灰狼个体Li的适应度计算函数为Fitness(L)=∑e∈ETcost(e)，计算得到组播树GT的开销，即为灰狼个体Li的适应度值。

Step6 个体适应度选优。通过比较个体适应度，选出适应度值最优、第二优和第三优的个体，分别赋值给α、β、δ。

Step7 灰狼狩猎行为。选择α、β、δ个体作为参照目标，当代灰狼群体展开狩猎行为，更新每一个灰狼个体的参数。个体L的每一维li取值表示该目标组播树中是否包含第i条链路，以α=[α1,α2,…,αM]为目标对灰狼个体L的每一条链路选取进行更新，具体步骤如下：

(10)

(11)

(12)

(13)

位置更新后得到新灰狼个体，完成一次灰狼个体的狩猎行为。

Step8 灰狼个体变异。以变异概率Pm对搜索后的每个个体的每一维进行变异操作。若更新后的种群中，当代最优个体优于种群历史最优个体，那么用该个体替换种群历史最优个体，否则保持不变。每一维的变异操作如下：

(14)

Step9 算法收敛判断。判断算法是否达到最大迭代次数Maxgen，满足则算法结束，输出历史最优个体best，以及对应的组播树；否则转到Step 4。

3 性能分析

本文所有实验运行的软硬件环境为：Windows 10 OS，Intel(R) Core(TM) i5-4210M CPU 2.6 GHz+8 GB RAM。所有算法采用Python 3.6 仿真。

3.1 仿真参数设置

为了验证GWO算法在求解组播树问题上的高效性，采用了4个不同的场景与遗传算法进行对比，来说明本文GWO算法的收敛性更好，能够得到更好的优化结果。场景设置如下：

场景1：节点数49，边数84，组播源节点：14，目的节点：{39,20,48,17}，带宽约束为8 Mb/s，不满足带宽约束的链路为1条。算法种群规模都为20，迭代次数为100。

场景2：节点数53，边数89，组播源节点：39，目的节点：{28,42,7,35,49}，带宽约束为8 Mb/s，不满足带宽约束的链路为1条。算法种群规模都为20，迭代次数为100。

场景3：节点数58，边数87，组播源节点：1，目的节点：{50,51,44,35,49}，带宽约束为8 Mb/s，不满足带宽约束的链路为1条。算法种群规模都为20，迭代次数为100。

场景4：节点数145，边数186，组播源节点：98，目的节点：{81,25,52,120,60}，带宽约束为8 Mb/s，不满足带宽约束的链路为2条。算法种群规模都为20，迭代次数为100。

3.2 实验结果分析

两种算法都运行20次，计算在4个不同场景下的历史最优适应度的平均值、历史最优适应度的标准差，以及算法的平均运行时间，如表1所示。

表1 两种算法结果对比

启发式算法是随机搜索的算法，具有一定的偶然误差，通过运行多次，可以在统计学上得到较为准确的性能评估。适应度平均值AVG和适应度标准差STD的计算公式分别如下：

(15)

(16)

式中:N=20，xi表示每一次运算运行得到的最优解。

图2为两种算法的历史最优适应度对比曲线。算法每次迭代过程中，产生一个当代种群最优解，与历史最优解比较，如果比历史最优解好，则替换历史最优解；否则不保留。将GA和GWO分别运行20次，对每次求得的历史最优适应度取平均值，得到最终的历史最优适应度。

(a)场景1

图3为两种算法的平均适应度对比曲线。将GA和GWO分别运行20次，对每次求得的平均适应度取平均值，得到最终的平均适应度。

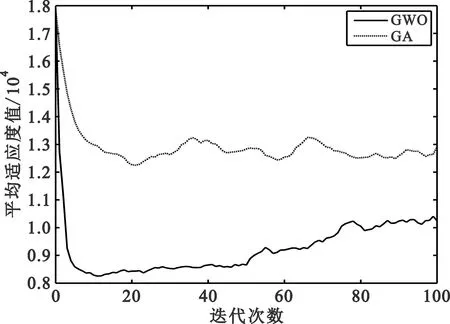
(a)场景1

通过对两种算法运行结果的对比分析，可以得到以下结论：对于节点度约束和带宽约束的组播路由问题，给定一个网络拓扑与种群规模，迭代次数相同的情况下，本文提出的基于灰狼优化算法的组播路由策略可以得到更好的优化结果，能够得到一棵开销更小的组播树。由于GA和GWO算法均是基于随机搜索的启发式算法，因此在算法迭代过程中容易出现性能波动。仿真结果表明，遗传算法优化结果波动较大，算法稳定性较差；与遗传算法相比，本文提出的基于灰狼优化算法的组播路由策略稳定性更强，同时算法的时间复杂度并没有增加，充分说明了本文提出的基于灰狼优化算法的组播路由策略的高效性。

4 结 论

针对无线网络中资源受限的组播路由问题，考虑网络节点的节点度限制和网络链路的带宽约束，以最小化组播路由开销为目标，本文提出了一种二进制编码方式的基于灰狼优化算法的组播路由策略。在给定的网络拓扑下，该策略可以迅速找到一棵包含源和目的节点的组播树，使得开销尽可能小。仿真结果表明，相比于遗传算法，本文提出的基于灰狼优化算法的组播路由策略能够得到一棵开销更小的组播树，并且在相同的时间复杂下具有更强的算法稳定性。