机间数据链系统的功率分配控制方法*

(西安邮电大学 通信与信息工程学院，西安 710121)

0 引 言

现代战争的实质为信息化战争，获胜的条件是对战场信息的掌握。数据链将指挥、控制、武器、探测等平台紧密地联系在一起，是战斗中信息传递的中枢环节。美军的战术目标指示网络技术(Tactical Targeting Network Technology,TTNT)数据链，就是一种高速、宽带、基于互联网协议的动态自组织网(Ad Hoc)数据通信网络系统，主要负责机载网络中的战术边缘网络组网。扩展频谱技术因具有抗干扰、固有的保密性等优势，可将其引入Ad Hoc网络中。因此本文中想定机间数据链模型基于码分多址(Code Division Multiple Access,CDMA)技术的Ad Hoc网络建立，网络节点间通信采用时分双工(Time Division Duplex,TDD)模式，通信节点利用同一时分多址(Time Division Multiple Access,TDMA)帧上的不同时隙收发信号。

功率控制技术[1-3]一方面是减小系统中能量消耗有效手段，一方面是要考虑在系统中多个条件下取得最佳方案。近年来，智能算法被广泛用在实际工程优化中，其中基于启发式多目标优化算法就成为工程优化领域的重要求解工具，它具有灵活度高、适用性广、求解效率高等优势[4]。文献[5]提出多目标灰狼算法解决雷达干扰资源调度多目标优化问题，能够得到最佳的调度方案。文献[6]在空军航材配置中建立多目标优化模型，提出多目标蚁狮算法(Multi-objective Ant Lion Optimizer,MOALO)得到一种有效的优化配置方案。文献[7]为了让无线传感器的网络覆盖率和通信能耗最优，使用引入了量子粒子的多目标粒子群(Multi-Objective Particle Swarm Optimization,MOPSO)优化算法，大幅提升了网络的稳定性。上述研究成果表明，不同群体智能算法应用于工程中行之有效。多目标优化算法有很多，如经典的MOPSO算法[8]、基于分解的多目标进化算法[9](Multi-objective Evolutionary Algorithm Based on Decomposition,MOEA/D)、较新提出的MOALO算法[10]等。这些算法都可解决多目标优化问题，但通常考虑两种优化目标，当目标函数增加，优化结果的Pareto前沿常常会远离真实Pareto前沿或跨度不够广泛等不足。灰狼算法[11](Grey Wolf Optimizer,GWO)有解决优化问题参数少、实现简单和收敛速度快等优点，多目标灰狼(Multi-objective Gray Wolf,MOGWO)算法[12]在此基础上增加多目标处理机制，增强了算法中个体的探索能力和全局搜索能力，在求解Pareto前沿时有一定的优势。

因此，针对想定战场上执行作战任务中机间数据链通信系统，为了抑制各节点的通信干扰，提高系统服务质量(Quality of Service,QoS)，降低被截获性能来保证任务完成，本文提出了一种基于MOGWO的机间数据链功率控制方法，以各节点功率为优化对象，建立多目标优化问题。为了有更快的收敛速度，对MOGWO算法中控制参数a引入指数函数，对于求解出的Pareto解集，利用选择准则取得最优功率分配解。仿真结果表明，与MOPSO、MOEA/D、MOALO、文献[12]原算法和恒定功率方法相比，本文提出的算法能够更好地满足通信需求，减少系统的发射功率并提高射频隐身性能。

1 系统模型

1.1 场景假设

考虑对敌方战场情况的侦察任务，采用以预警机为中心，半径200 km内有5架战机分布[1]的编队。各战机在同一时隙内战机采用全向天线发射向预警机发送信息，存在被敌方无源接收机截获概率。建立通信模型如图1所示。

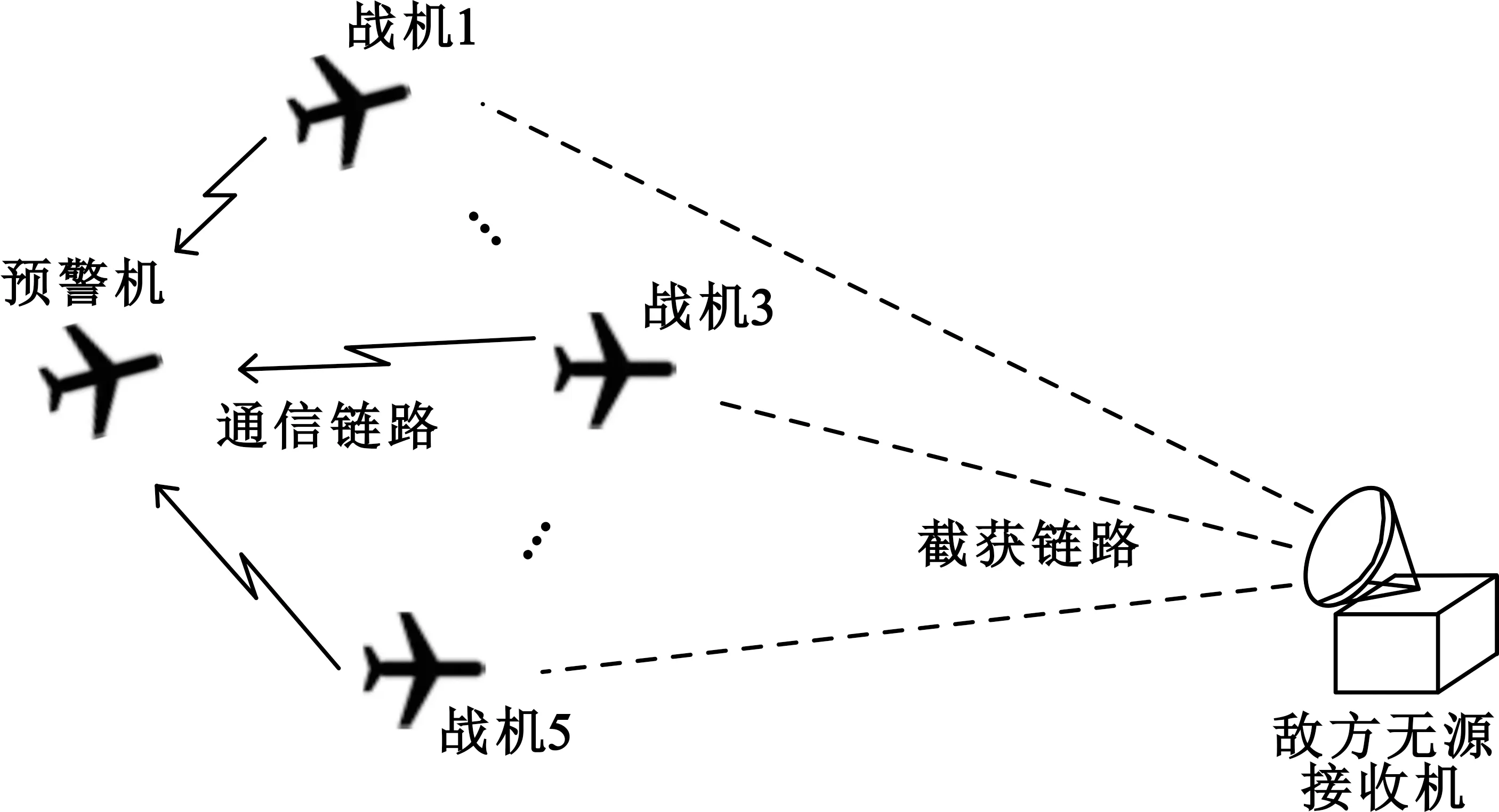
图1 想定数据链网络上行链路通信模型

1.2 截获概率

截获概率(Probability of Intercept,POI)是电子战系统的重要性能指标，即在特定威胁信号最初到达接收机系统位置之时直至接收机系统接收不到它时的时间范围内，接收机系统检测到该威胁信号的概率。

如图2所示的一个多用户数据链网络的场景[7]，存在一个无源接收机对用户传输信号进行截获。

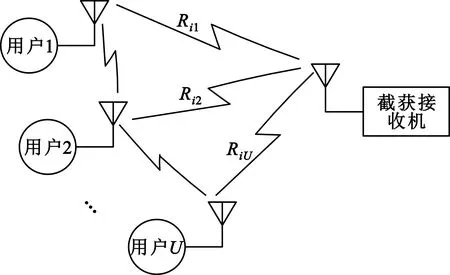
图2 多用户截获场景

图2描述了无干扰时多用户通信的截获场景。属于能量检测器的截获接收机具有从通信网络中处理多用户信号能量的能力，因此进入截获接收机的信号为

(1)

式中：sj(t)是来自第j个发射机的信号，t为时间，U是用户数量，n(t)是高斯白噪声。第j个信号的截获信噪比为

(2)

式中：NSI为噪声的功率谱密度;PTj是在第j个发射机发射信号sj(t)的平均功率;GTjI和GITj分别是发射天线增益和截获接收机天线增益;αIj(f,RIj)为第j个截获链路上的传输损耗;LIj是大气损耗;Tj=min{TI,TSj}，TI是截获时间，TSj为信号的持续时间。

若均为全向天线GC，接收机噪声NSI≈N0，大气损耗大致相等LIj≈LI，当Tj=TSj，公式(2)可写为

(3)

为方便度量，认为进入截获接收机中的总能量由网络中信号能量叠加组成，因此在截获接收机位置处接收到的总信噪比为

(4)

对于固定虚警概率PF和时宽带宽积T1W1，信噪比与探测概率之间的关系如下：

(5)

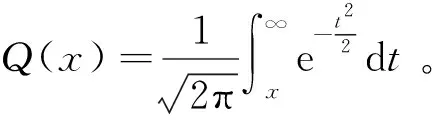
数据链射频信号被无源探测系统截获的概率用PI表示。PI是空间、时间、频率域三重窗口的重合概率和能量域检测概率的乘积。假设截获接收机在空、频域对准，则无源系统对数据链信号的截获概率可以表示为时域窗口的重合概率和能量域检测概率之积，因此，

(6)

1.3 建立数学模型

编队内有N个节点通信，节点i(i∈N)与预警机的距离为di，gi和pi分别表示第i个节点的信道增益和发射功率。考虑某一通信业务，对于此类业务设定目标信干噪比(Signal-to-Interference plus Noise Ratio，SINR)值γtar和最小SINR值。σ2表示接收机背景噪声，G为通信系统内的扩频增益，得到接收节点的SINR表示为

(7)

建立功率控制的数学模型，如式(8)：

(8)

式中：f1表示最小化系统中各节点传输功率和的目标，pmin为最远节点满足通信的功率值；f2表示各个节点能够正常通信来满足QoS需求，各节点的SINR与目标SINR越接近越好；f3表示最小化通信时截获概率。

考虑在求解过程中需要使得那些发射功率大、对系统干扰起严重影响的节点进行惩罚，以保证其他节点的正常通信。对f1的优化如下：

(9)

式中：α为惩罚因子。针对上述优化问题，使用多目标灰狼算法进行求解。

2 多目标灰狼算法

2.1 灰狼算法(GWO)

GWO[11]中依据解决问题的优劣性来模拟划分灰狼的社会等级，最优解作为α狼(头狼)，第二和第三最优解分别命名为β狼和δ狼，剩下的候选解被称为ω狼。在α狼带领下，搜寻猎物并逐渐接近，待确定猎物位置后，形成包围并逐渐缩小范围，最后实施攻击。

在狼群狩猎过程中，按照式(10)进行狼群的位置更新：

(10)

式中：t为目前迭代次数，A和C称为系数，Xp是猎物的位置，X是灰狼的位置。a在整个迭代中线性的从2递减到0，r1和r2是[0,1]中的随机向量。灰狼利用式(10)更新其在猎物周围任意随机的位置。

在灰狼捕获猎物中，会保存灰狼社会等级中前三个α、β、δ狼的解决方案，ω狼按照它们的位置进行更新：

(11)

式中：Dα、Dβ、Dδ分别为t次迭代中α、β、δ狼与ω狼之间的距离。

在迭代中，A为[-2a,2a]之间的随机值。当A在[-1,1]时，狼群会向猎物收敛，当满足最终条件时获得全局最优解。

2.2 多目标灰狼算法(MOGWO)

2.2.1 多目标优化

多目标优化问题是指在一个系统中使多个目标在某种约束条件下同时达到最优的问题。在多目标优化中，通过Pareto支配关系来判断解的优劣性。支配关系定义如下[11]：

对于任意两个解向量x与y，假设在最小化问题f(f1,f2,…,fo)中，称x对y形成支配关系，当且仅当[∀i∈{1,2,…,o},fi(x)≥fi(y)]∩[∃i∈{1,2,…,o},fi(x)≥fi(y)]，就称x支配y，表示解x优于解y，o为目标函数个数。多目标优化问题就是在可行解中找到那些不被其他解支配的解(非支配解)，所有的非支配解集称为Pareto前沿。

2.2.2 MOGWO

相对于灰狼算法，MOGWO主要增加了存档(archive)和领导者选择机制两个部分[12]。

(1)存档

存档用来保存或检索当前的非支配解。存档关键的是解在进入存档前的控制机制。在算法迭代中，将当前得到的非支配解与存档中的解进行比较。另外，网格机制运行方式如下：对存档中的所有解按照目标函数值的距离进行分组，首先计算所有解的目标函数f(f1,f2,…,fo)，分别找到每一个目标函数的极值fimax和fimin；接着对每一个目标函数，以极值为上下界，平均分j个区间(1～j)；最后，每一个解将其对应的目标值fi对应的区间记为ji，即(j1,j2,…,jo)就是该解所在的分段。

(2)领导者选择机制

仅依靠Pareto支配关系难以直接确定出3个非支配解，采用领导者选择机制在存档中来选择头狼，选择是通过轮盘赌方法进行的，每个解被选择的概率与所在分段的个数成反比：

(12)

式中：c是大于1的常数，Ni是第i段中获得的Pareto最优解的个数。

为了保证算法有好的探索能力，将文献[12]中原算法的a从线性递减为0，改为非线性方式递减至0，表达式为a=2-2×(it/Maxit)5。结合上述内容，基于MOGWO的机间数据链功率优化算法流程图3所示。

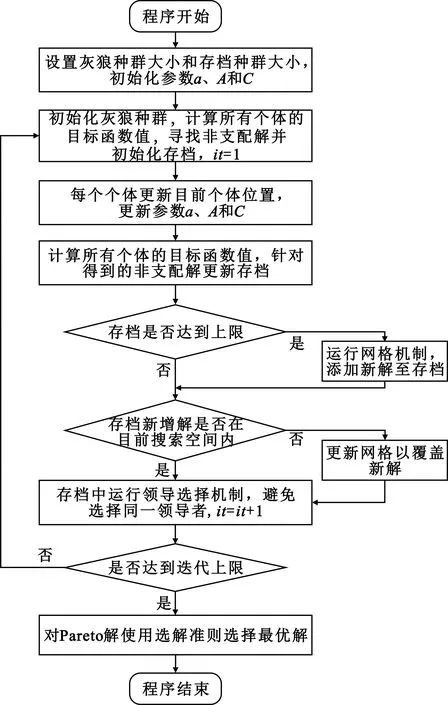
图3 MOGWO算法流程图

2.2.3 算法计算复杂度分析

假设只考虑整个算法在某一次迭代过程中，算法的基本操作模块的复杂度。灰狼种群大小用N表示，若存档与种群大小一致，目标函数的个数用m表示，本文算法的复杂度与文献[12]算法复杂度保持一致，为O(mN2)。文中实验使用经典的MOPSO、MOEA/D和新的MOALO算法进行比较，对它们计算复杂度进行分析。

MOPSO算法通过确定粒子的局部最优值和全局最优值，粒子通过自身的经验和群体中最好的经验来更新下一步的运动，再依据存档中粒子的密度信息选择粒子，得到Pareto解集。计算复杂度方面，N为粒子群数量，存档值与其保持一致，则复杂度为O(mN2)。

MOEA/D由分解算法和进化算法组成。分解算法将多目标问题转化为指定数量的单目标优化子问题(个数为N)；进化算法会对每一个子问题，利用一定数量、与其相邻的子问题(个数为T)的信息，在每次迭代中同时对各个子问题进行优化求解。多次迭代，得到Pareto解集，计算复杂度为O(mNT)。

MOALO是由蚂蚁随机不断探索解空间，它会掉进蚁狮(局部最优解)的陷阱，蚁狮会根据蚂蚁和蚁狮的评价值来更新，从中选取最优评价值的蚁狮为全局最优。利用与MOPSO相似的多目标机制，得到Pareto解集。计算复杂度方面与MOPSO保持一致为O(mN2)，其中N为蚂蚁个数。

3 仿真分析

3.1 参数设定

对模型进行参数设置，部分参数数据参考文献[1-3]。误码率PE为10-3～10-4，采用QPSK调制方式，设置接收处目标SINR为9 dB，最小SINR设为7 dB;pmin为135 W;惩罚因子α为30。表1为具体想定参数内容。

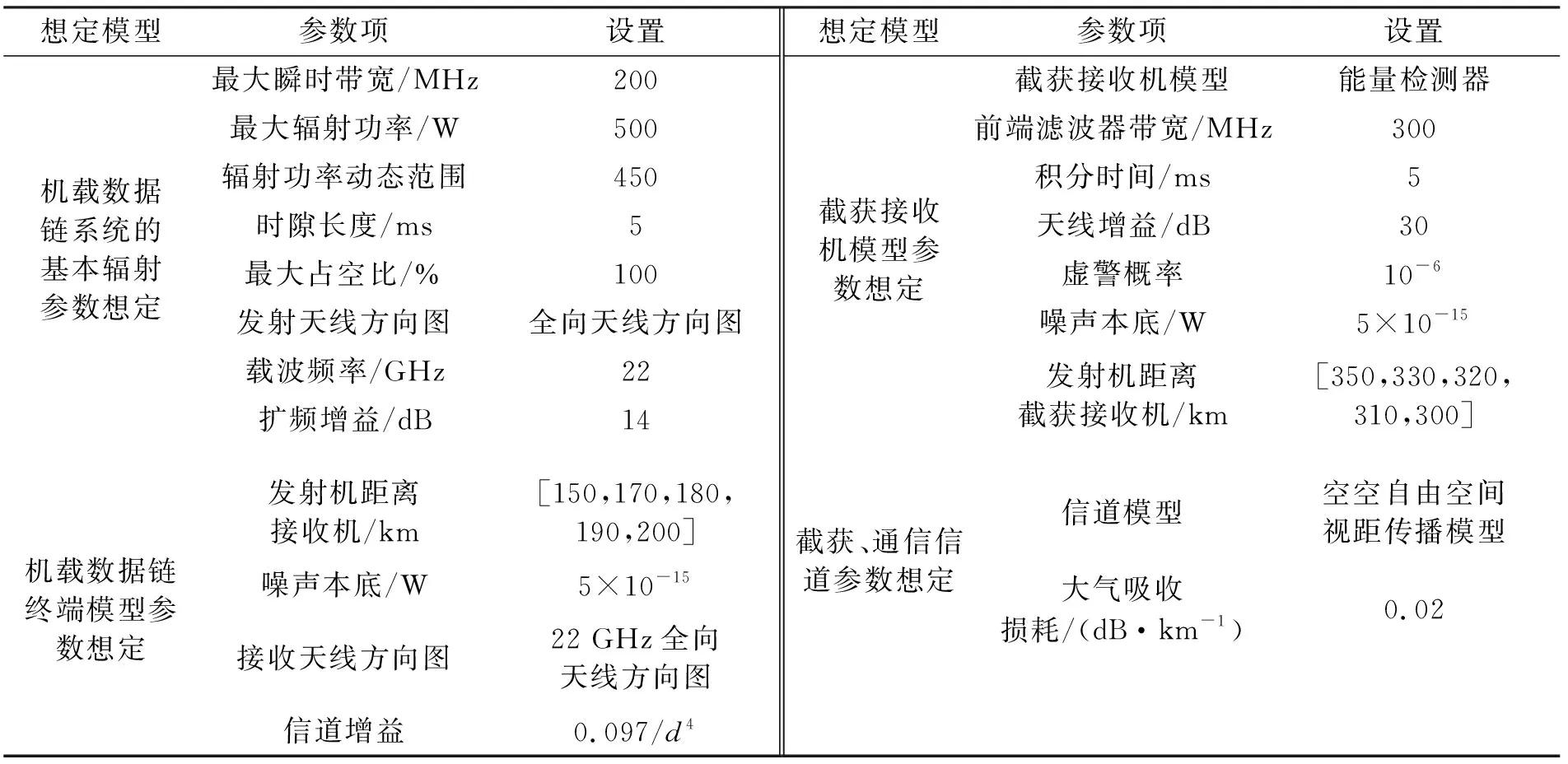
表1 具体想定参数内容

3.2 仿真

利用MOGWO求解多目标问题。仿真环境为Matlab2016a，CPU为i7-4702m，仿真参数见表2。MOGWO一次运行结束所得存档中Pareto解集如图4所示。

表2 四种不同算法的仿真参数

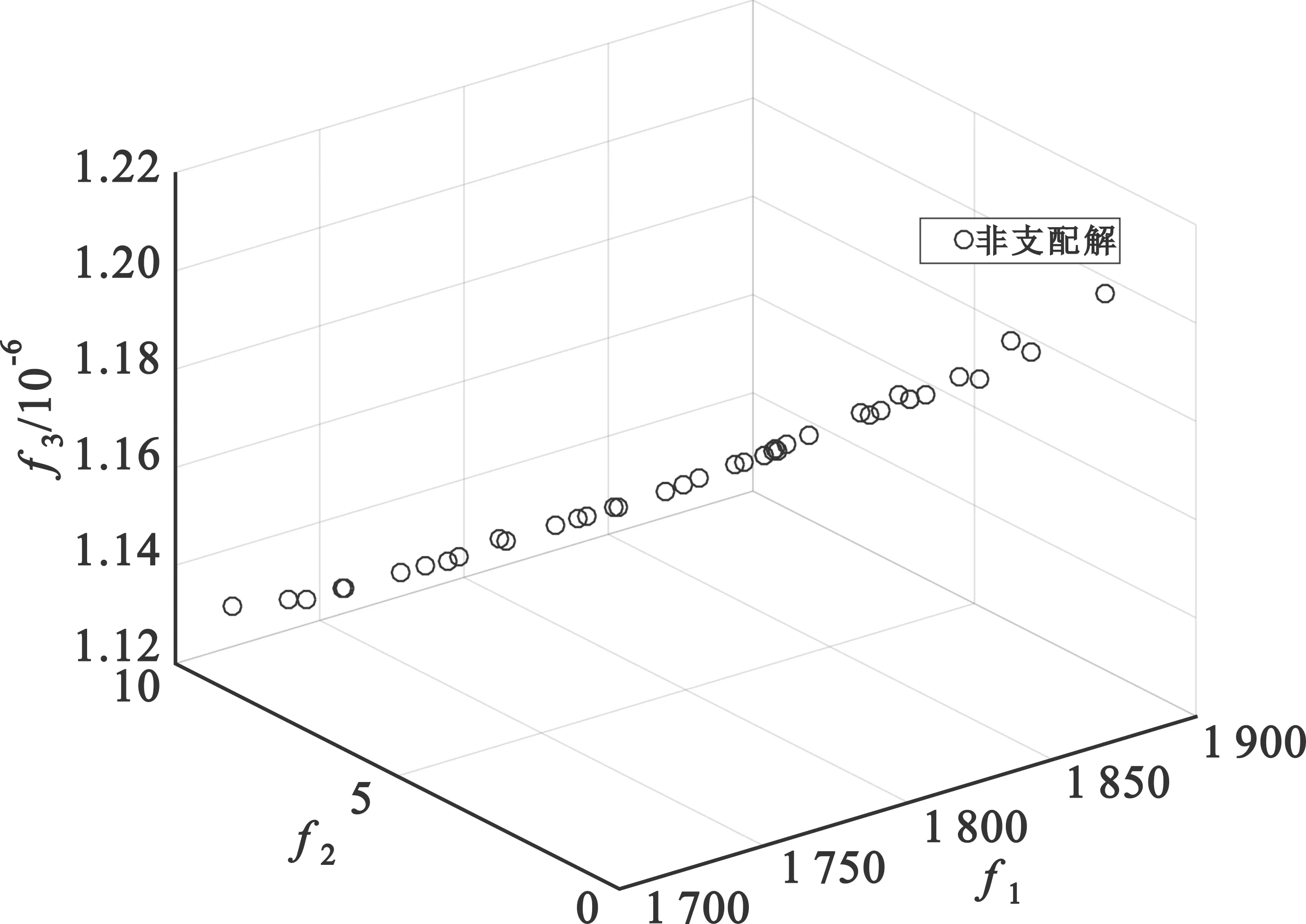
图4 MOGWO的Pareto解集

图4中三个坐标轴分别代表三个目标函数，图中散布的点即为优化所得解。从图中可以看出整个非劣解集分布较为分散，在算法迭代中使用网格机制，将新的解插入到最不拥挤的段上，使得解集更具多样性。

算法结束后会得到Pareto解集，根据对功率、SINR和截获概率的要求设定权重系数。定义选解准则如下：

(13)

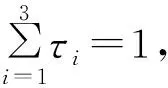
3.2.1 MOGWO与MOPSO、MOEA/D和MOALO算法比较

依次使用不同算法运行求解，再用选解准则分别对各自Pareto解集进行选择，图5给出了不同算法依据准则选出的最优解，图6描述了不同算法解对应的接收机处SINR值与目标SINR值。四种算法对应最优功率解的平均值大小如表3所示。

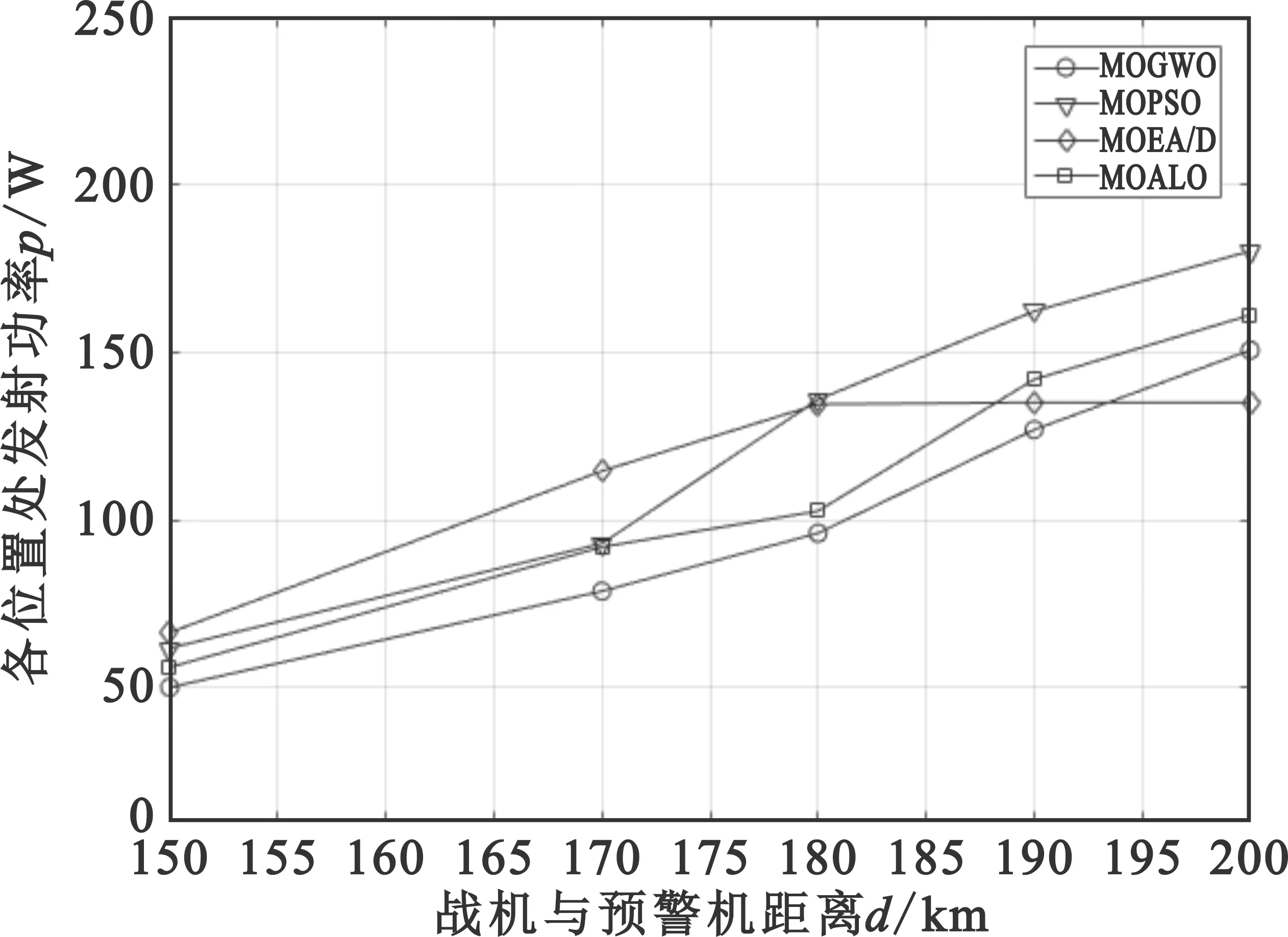
图5 不同算法所得功率分配结果

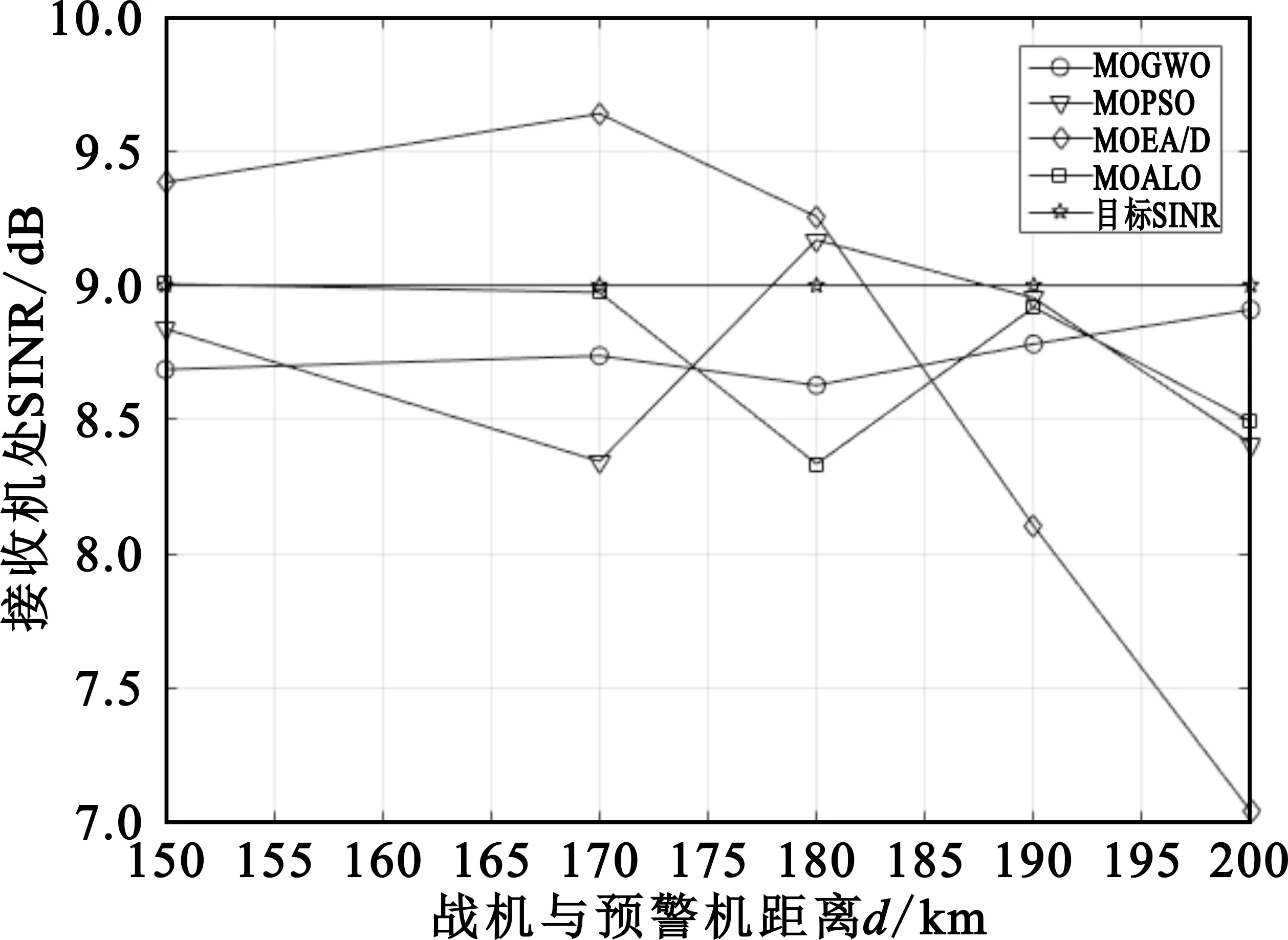
图6 不同算法所得功率在接收机处的SINR值

表3 不同算法对应解得平均值

图5中MOGWO、MOPSO、MOEA/D和MOALO算法求解出的功率分配值在给定无源截获接收机位置下的截获概率分别为1.204 1×10-6、1.218 4×10-6、1.214 1×10-6和1.204 9×10-6，相比之下MOGWO有更低的截获概率。从图5和图6可以看出，与MOPSO、MOEA/D和MOALO算法比较，本文的MOGWO算法能够求解出较小的各节点的功率分配值，有效减小各节点的发射功率，且能保证QoS要求，即各节点的SINR值能在接收机处保持较稳定同时接近目标SINR值。MOEA/D算法由于将多目标问题分解成多个子问题，利用相邻子问题的解同时优化多个子问题，但在此问题下存在容易陷入局部解的情况，求出的解在接收机处的SINR与另三种算法相比有明显波动。在相同仿真参数下MOPSO和MOALO解的收敛性和多样性较为不足，无法得到更优解，所得功率分配值在接收机处的SINR值存在一定幅度的波动情况。

为了比较本文所提算法与其他三种算法求得解的优劣程度与算法的稳定程度，对四种算法重复进行10次独立实验，使用不同算法求解出的解所对应SINR值与目标SINR值的接近程度以及SINR值的波动情况来更加直观地说明，采用均值与标准偏差来比较，定义如下：

(14)

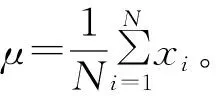
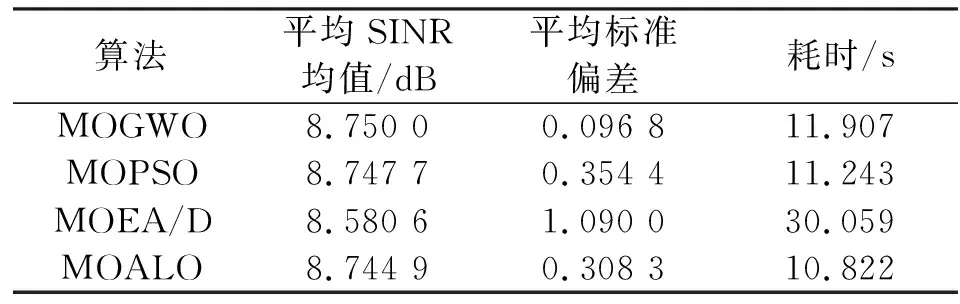
表4 不同算法解的优劣表现

通过表4中的数据可以看出，在算法搜索效率方面，MOPSO、MOALO和MOGWO三者的计算复杂度一致，所以求解时间较为相似。MOEA/D虽然在计算复杂度方面低于其他三种算法，但在寻优时易陷入局部最优解难以跳出以至时间花费较多。在算法的寻优方面和稳定性方面，多次重复实验下MOGWO的平均SINR均值最接近目标值，并且在平均标准偏差上表现最好，即可解出各节点最优的功率分配方案，以及各节点之间干扰情况最小，很好满足各节点的QoS要求。MOALO算法中由于蚂蚁个体的位置更新十分依赖精英蚁狮的信息，会导致问题过早收敛，不利于寻找全局最优解。MOPSO算法计算过程中粒子对于历史最优值和全局最优值的选择有较大随机性，使收敛性和分布性不足，导致这两者算法的解在平均标准偏差方面与MOGWO算法的解相差较大，说明没有很好地分配各节点处的发射功率，各节点之间存在干扰，没有很好保证各节点的通信质量。MOEA/D算法在利用相邻问题的信息对一系列子问题优化时，不容易跳出局部最优解，使得解无法达到最优，体现在有较大的平均标准偏差值，所得平均SINR均值也离目标值最远，即未能得到较好的功率分配方案，导致各节点的相互干扰情况最为严重。本文算法是3只不同的头狼在整个解空间下进行引导搜索，能够对空间充分搜索，有效克服局部收敛的问题，参数a的非线性减小与网格机制和领导选择机制都增强了算法的求解能力，很少出现劣解，提高了算法的稳定性。因此，在相同实验条件下，MOGWO算法求解出解的质量明显好于其他三种算法。

3.2.2 与恒定发射功率方法和文献[12]原算法进行比较

恒定发射功率方法为当机间数据链内各节点以pmin为发射功率，其他条件保持不变。文献[12]原算法的仿真参数与表2中MOGWO一致。三种方法在接收机处对应的SINR值的变化情况如图7所示。

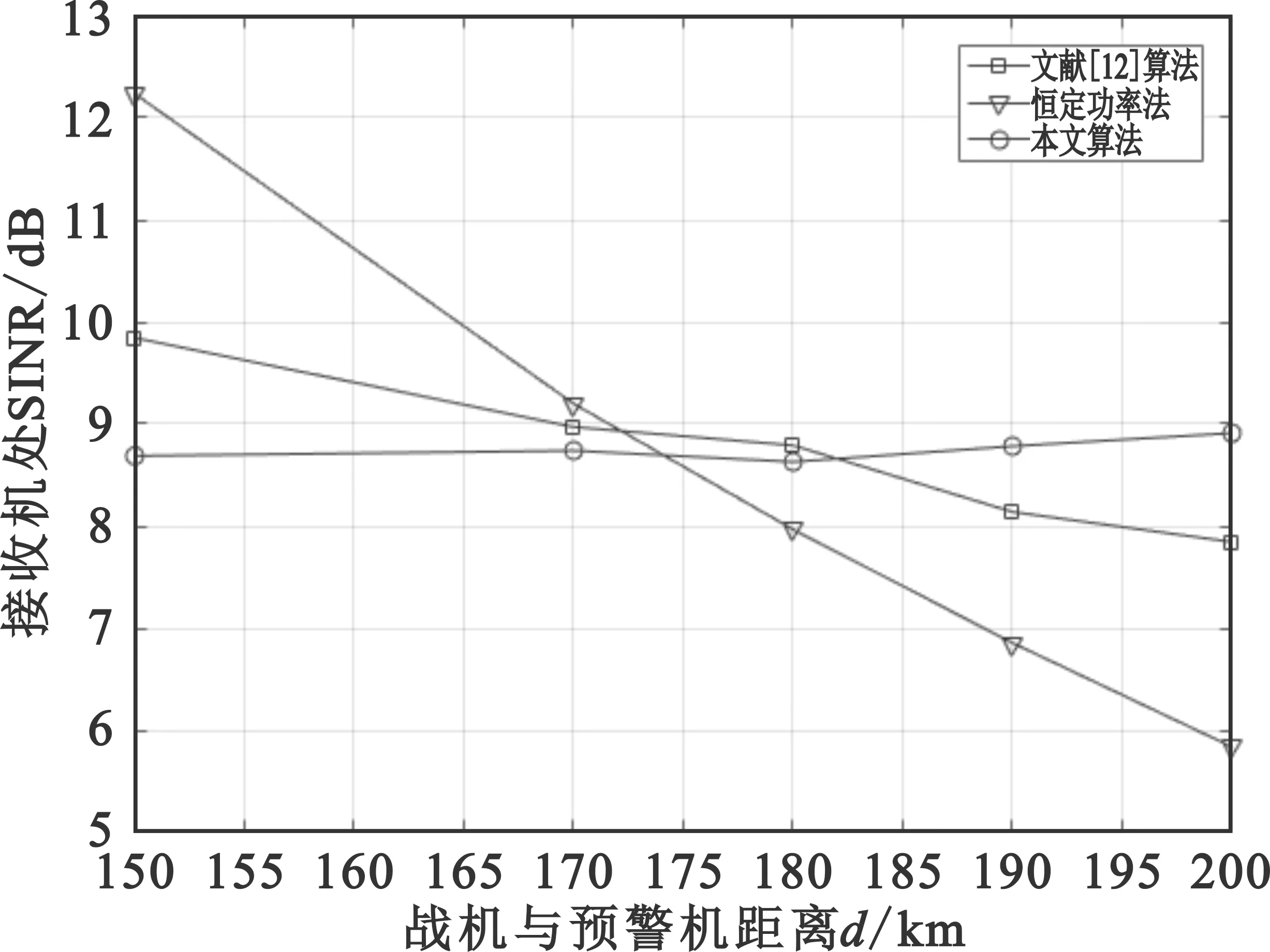
图7 本文算法与恒定功率方法、文献[12]算法对比图

由图7可知，文献[12]算法在解决此模型问题中收敛至局部解，使得各节点之间仍然存在干扰，造成接收机处SINR值分配不合理，而本文算法调整算法参数a为指数函数，前期增加探索，后期加快收敛至最优。在恒定功率下，SINR的值随着距离的增加不断下降，说明在距离近处发射机的功率会严重影响远处发射机在接收机处的SINR，造成其不能接收数据的情况。总体来看，本文MOGWO算法对功率分配更加合理，使在接收机处的SINR波动更小，能更好地保证各位置处的通信能力。

4 结 论

本文想定作战任务中机间数据链系统，从降低系统的功率与保证不同位置处战机通信性能和数据链射频隐身性能入手，提出了基于多目标灰狼算法的数据链功率优化方法。该算法在想定的空间位置处，在上行通信链路的同一时隙内以最小化各战机辐射功率、最小化接收机处各信号SINR与目标SINR和最小化系统截获概率为目标，利用多目标灰狼优化算法对想定模型进行功率控制。仿真结果表明，本文算法与MOPSO、MOEA/D、MOALO相比有更好的寻优能力和稳定性，与文献[12]原算法相比能克服陷入局部解的不足，与恒定辐射功率方法相比能更好地减小SINR波动，满足不同位置处通信能力，且具有较好的射频隐身性能。