基于循环前缀频域自相关的OFDM信号频谱感知*
2021-05-31赵迎新王乐耕赵婉楠刘之洋
赵迎新,王乐耕,赵婉楠,吴 虹**,刘之洋
(1.南开大学 电子信息与光学工程学院,天津 300350;2.天津市光电传感器与传感网络技术重点实验室,天津 300350)
0 引 言
随着高速无线通信技术的发展,人们对无线通信业务的需求日益增长,对支撑无线通信系统演进的关键因素——频谱资源的需求也迅速增长,从而导致频谱资源日益紧张,影响着无线通信研究领域中新技术的应用和发展,成为制约无线通信发展的瓶颈。
目前,由于信道传输性能较好,6 GHz以下频段仍然是信号传输的主要频段,但是该频段的大量频谱已被现有的通信系统占据。依据静态频谱分配机制,即将无线频谱资源以固定的形式划分为互不重叠的频段,并以独占的方式分配给授权用户,频谱资源在时间和空间上将不同程度地被闲置,资源利用率非常低。因此,迫切需要动态频谱共享技术[1]突破固定频谱分配的模式,提高频谱效率,这也是解决频谱资源紧张和频谱资源浪费之间矛盾的有效手段。
认知无线电技术[2-3]利用空闲的授权频谱,是实现动态频谱共享的关键技术之一,能够极大地提高频谱利用率[4]。频谱感知是应用认知无线电进行动态频谱管理的前提和基础。频谱感知在短时间内以较高的检测概率和较低的虚警概率识别频谱占用情况,进而正确检测到空闲频谱,发现频谱接入的机会。频谱感知技术很大程度上决定了认知无线电系统的整体性能。因此,频谱感知,尤其是能够准确快速检测宽频带的频谱感知技术,成为认知无线电领域研究的热点。常见的频谱感知方法有循环相关滤波检测[5-6]、能量检测(Energy Detection,ED)[7-9]、循环平稳检测[10-12]等。但每个检测方法都有一定的不足,例如能量检测算法计算复杂度低,且易于实现,但是算法性能受噪声影响较大,在实际通信系统中很容易受到噪声不确定性的影响;循环平稳检测类算法多在时域进行,适合主用户与频谱感知的带宽相匹配的情况,即整个带宽只存在主用户信号与噪声或者只存在噪声,无法解决宽带信号的频谱检测问题。尤其是一些特殊场景,如湿度的变化、环境的干扰及设备的非线性带来的噪声功率的随机波动,噪声不确定性[13]比较严重时,无论检测时间多长,微弱信号都很难完全识别出来。这种无法知道授权用户先验信息,并且信号受噪声不确定度影响较大的情况,在低信噪比环境下,直接采用能量检测的方式对接收信号进行频谱感知,势必会影响到系统性能,使得检测结果不可靠。
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术可以有效地提高频谱效率,缓解当前较为紧张的频谱资源形势,同时,具有更强的抗多径干扰能力,已经广泛应用于3G、4G、5G[14]、无线局域网等无线通信系统中。未来认知无线电频谱感知过程中,授权用户信号大多数将是得到广泛应用的OFDM信号。可以利用OFDM信号的典型特征完成授权用户信号的检测,从而完成频谱感知。
本文研究一种适用于OFDM系统的频谱感知方法,利用信号区别于噪声的某种典型特征,提出一种抗噪声性能强且复杂度相对较低的频谱感知算法。与能量检测算法相比,本算法具有较强的抗噪声性能,在信噪比较低或噪声不确定度大的场景下,具有更好的检测效果;与时域的循环平稳类算法相比,本算法可以用于主用户与频谱感知的带宽不匹配的情况,因此更加适用于实际的通信系统。
1 系统模型与问题描述
OFDM技术为了最大程度地消除码间串扰(Inter-symbol Interference,ISI),在每个OFDM符号之间插入保护间隔。通常采用循环前缀(Cyclic Prefix,CP),即将OFDM信号尾部对应长度的数据添加到保护间隔内,如图1所示。一个OFDM信号的长度为Ns=Nc+Nd,Nd表示OFDM信号的有效数据长度,Nc表示循环前缀的长度。本文利用循环前缀给OFDM信号带来的循环平稳特征,将循环前缀自相关算法应用到频谱感知技术中。
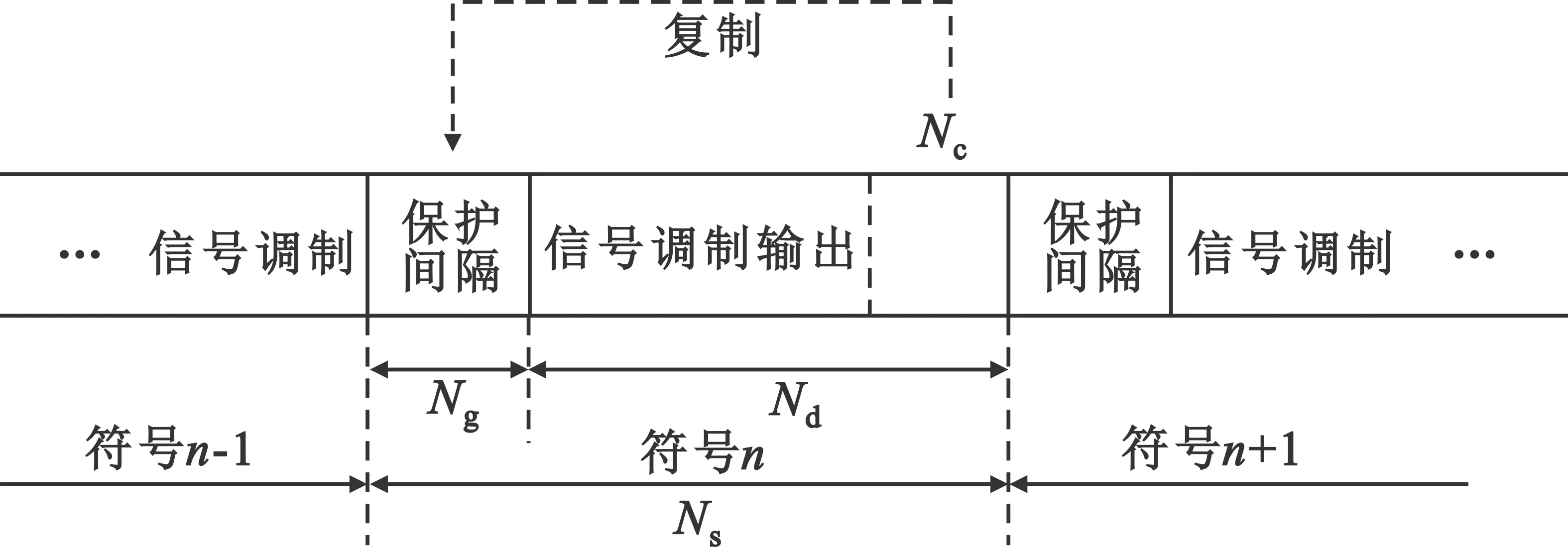
图1 OFDM添加循环前缀示意图
在频谱感知过程中,认知用户检测来自主用户发射的信号,由此确定主用户对频谱的使用情况,并判断是否有空闲的频谱资源可以利用。频谱感知可以根据频谱使用情况建模成二元假设判决过程,H0表示主用户不存在,H1表示主用户存在,则二元假设模型如式(1):
(1)
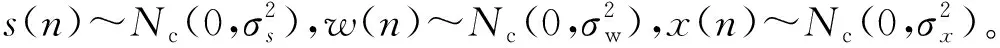
2 算法原理
2.1 单门限频域循环前缀自相关算法
在认知无线电系统中,很可能出现主用户与频谱感知的带宽不匹配,即带宽中既存在主用户信号和噪声又存在认知用户信号,并且信号受噪声不确定性影响严重。此时,认知用户检测一段频谱,该段频谱没有被主用户占用,认知用户接入该频谱;但如果主用户再次出现,将会造成认知用户与主用户信号的重叠,如果有其他认知用户检测该频段,将出现检测统计量太小导致检测不到主用户存在的情况。为解决上述问题,本文提出一种频域循环前缀自相关算法(Frequency Domain Cyclic Prefix Autocorrelation,FD-CP-AC),算法过程如图2所示。
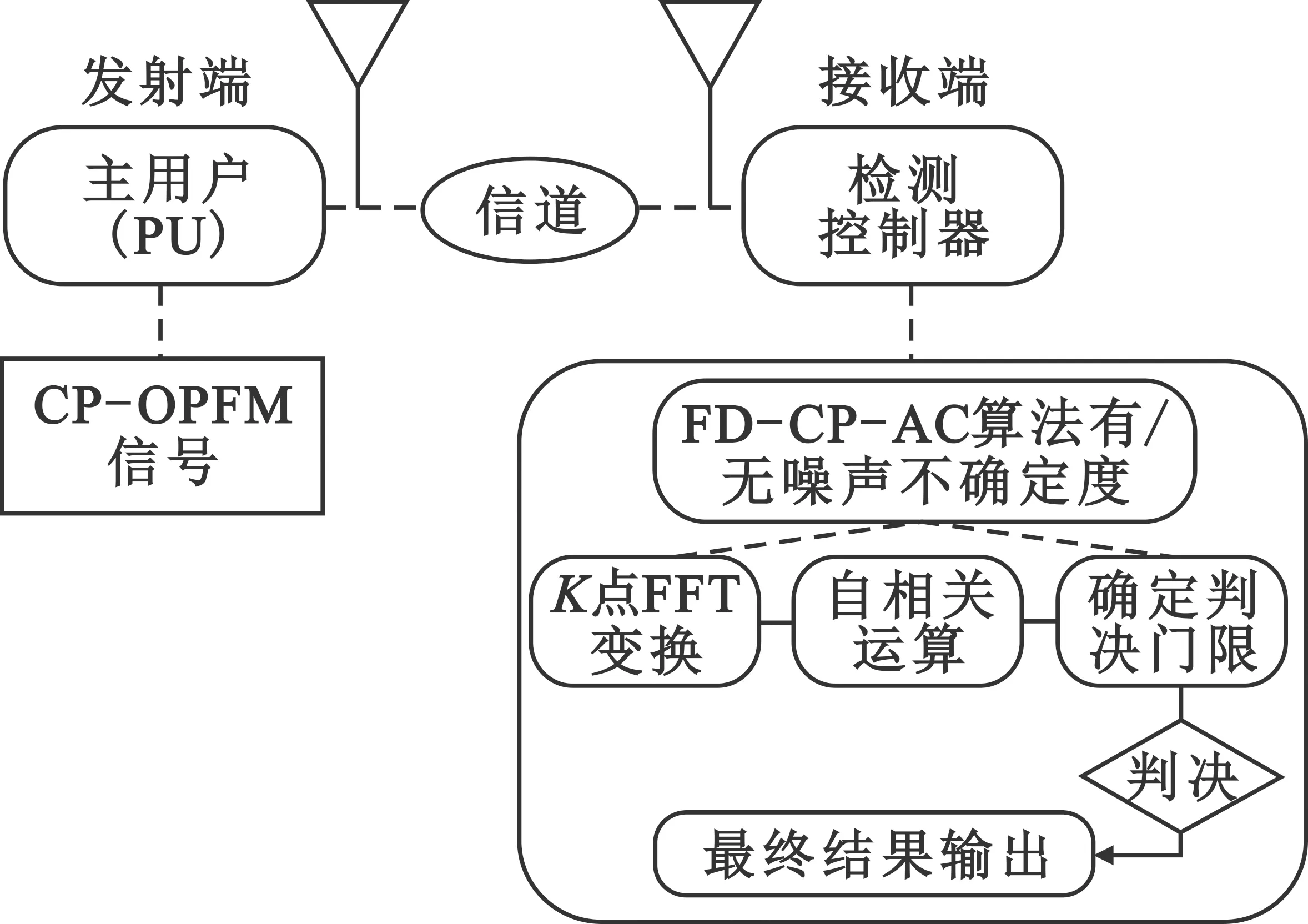
图2 FD-CP-AC算法过程
首先将接收到的时域采样信号分组,然后对每一组数据分别进行快速傅里叶变换(Fast Fourier Transformation,FFT)变换,变换后的数据为yk,m,其中k=1,2,…,K表示频域中每个子带的标号,m=1,2,…,M表示每个子带上采样点的标号。若xk,m表示主用户信号在第k个子带上第m个采样点所对应的数据,则对应的噪声为wk,m。算法根据频谱使用情况,在频域建立二元假设判决模型如下:
(2)
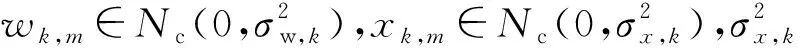
本文频域循环前缀自相关算法的检测统计量为
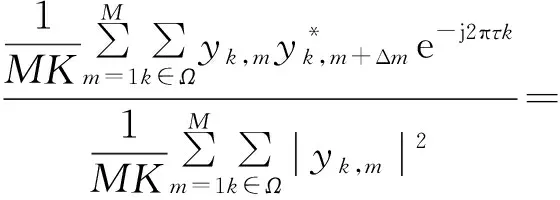
(3)
式中:Ω表示所有子频带集合,M表示每个子频带上采样点的总数量,整个检测频段上采样点数N可表示为N=K(M+Δm)。频域循环前缀自相关算法的检测统计量服从高斯分布。
主用户不存在的情况下,可以表示为
(4)
虚警概率为
(5)
故判决门限γ为
(6)
主用户存在的情况下,检测统计量CY(τ)中包含信号和噪声,故检测统计量服从如下分布:
(7)
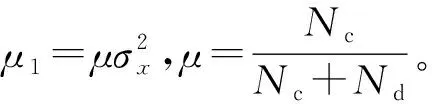
Pd=P(CY(τ)>γ|H1)=
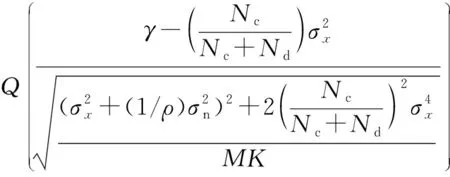
(8)
2.2 双门限频域循环前缀自相关算法
双门限频谱检测是在单门限的基础上增加一个门限,以此提高检测的可靠性。其中设有λH和λL两个判决门限,检测统计量可能出现的范围分为主用户存在、检测失败、主用户不存在三种情况。
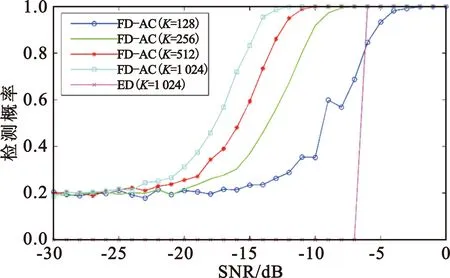
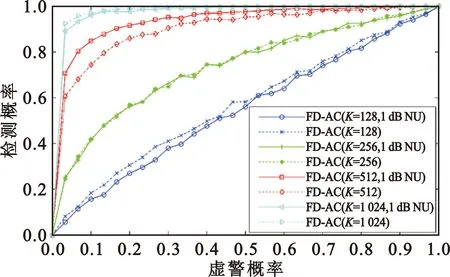
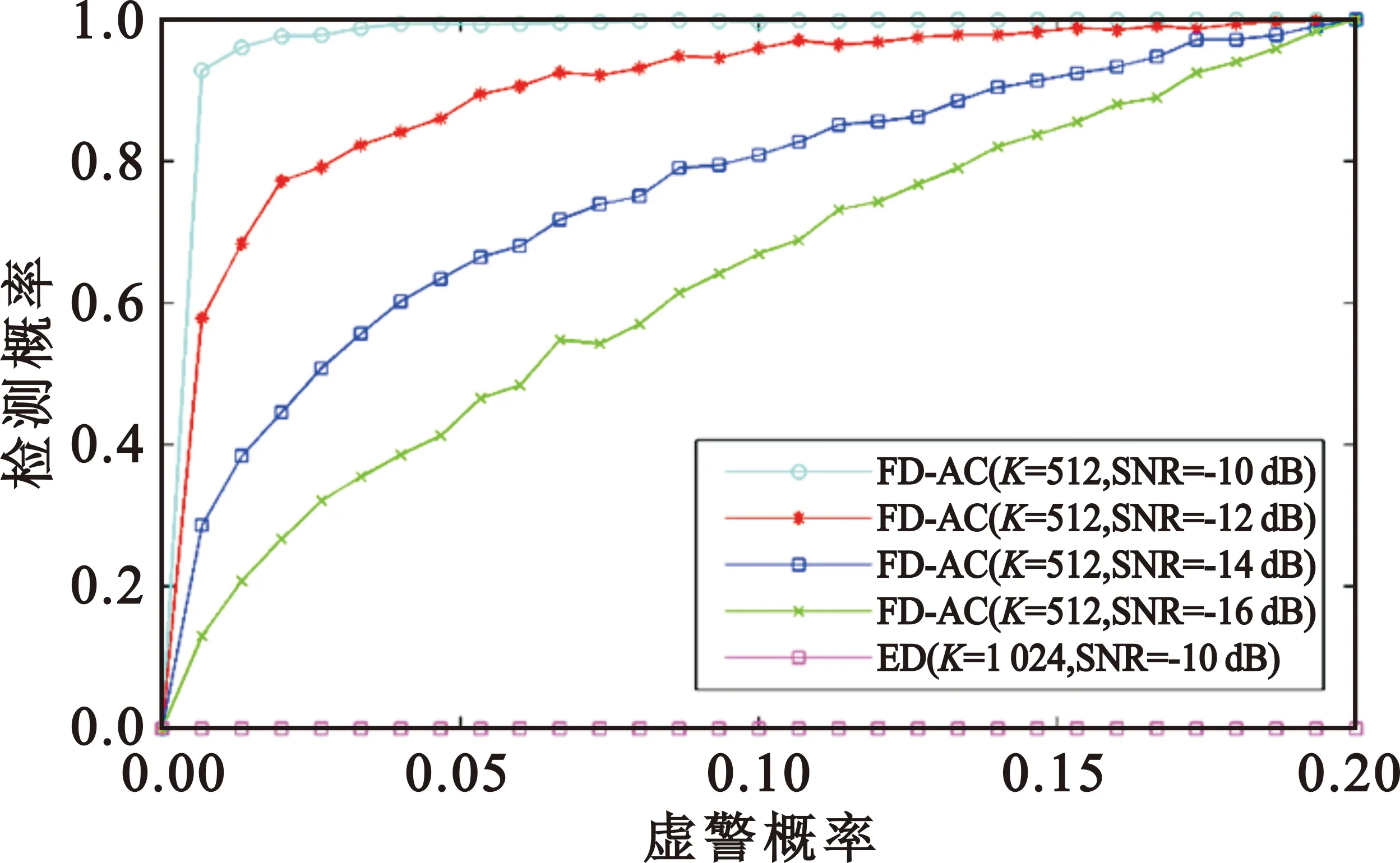
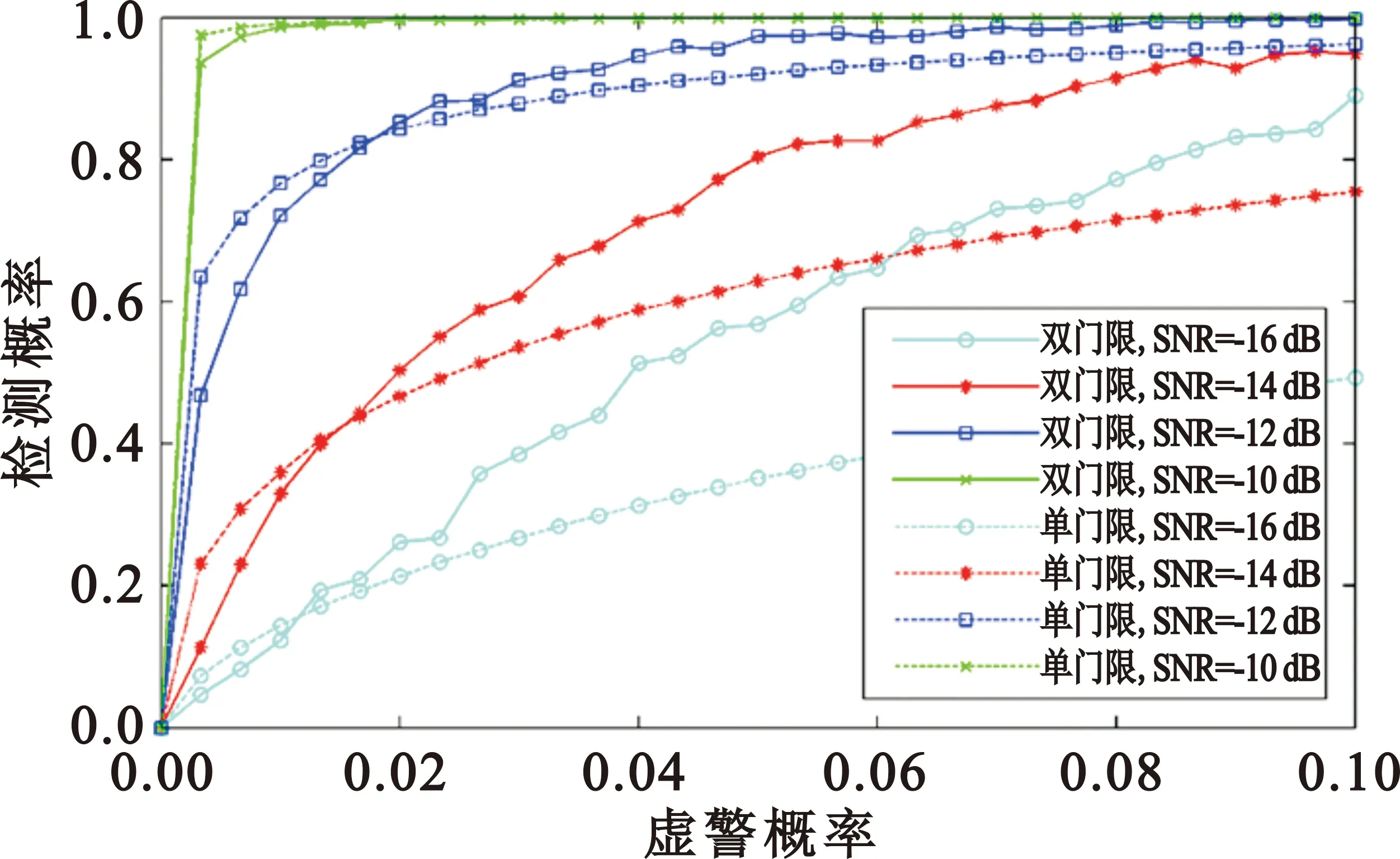
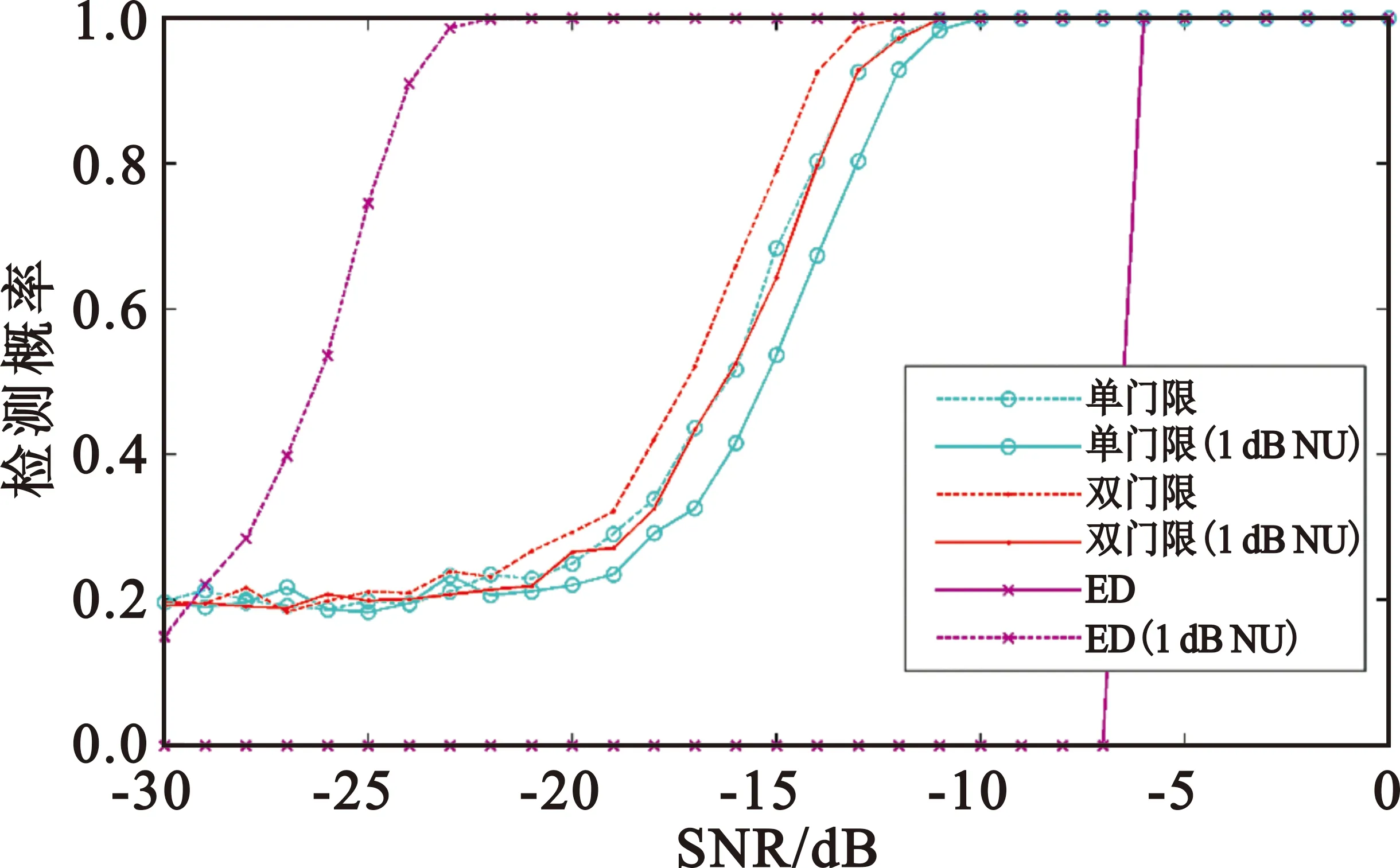
本文建立双门限频域循环前缀自相关检测模型。首先认知用户进行双门限FD-CP-AC检测,当检测统计量T>λH时,认为主用户存在;当T<λL时,认为主用户不存在;当λL 主用户不存在的情况下,该算法存在两种虚警概率。一种是认知用户可以判决,即检测统计量落入可判断区间,推导虚警概率Pf1为 Pf1=P{CY(τ)≥λH|H0}=Qf[1-P1(λL≤CY(τ)≤λH|H0)]。 (9) Pf2=P{λL≤CY(τ)≤λH|H0}= Qf2P(λL≤CY(τ)≤λH|H0)。 (10) 主用户存在的情况下,该算法同样也存在两种检测概率。一种是检测统计量落入可判断区间,推导检测概率为 Pd1=P{CY(τ)≥λH|H1}= Qd1[1-P(λL≤CY(τ)≤λH|H1)]。 (11) 其中: (12) 另一种是认知用户将检测统计量直接与已知设定的判决门限进行比较,推导检测概率为 Pd2=P{λL≤CY(τ)≤λH|H1}= Qd2Pi(λL≤CY(τ)≤λH|H1)。 (13) 其中: (14) 本文分别在不同采样点数、无噪声不确定度和1 dB噪声不确定度,以及不同信噪比情况下,对频域自相关算法进行仿真分析,并与传统的能量检测算法对比说明。考虑OFDM频谱检测的实际场景,本文仿真参数设置为:采样频率20 MHz,OFDM符号有效数据长度为64,循环前缀的长度为16,每个子带上的采样点数为100,子带个数为1 024、512、256、128,子带个数不同,频谱感知算法性能不同。 在虚警概率Pf=0.1、噪声不确定度为1 dB的情况下,检测概率随着划分子带数的增多而增大。由图3可知,在相同的信噪比情况下,K=1 024时的检测概率最高,性能优越,并且远优于能量检测算法;在噪声不确定的应用场景下,能量检测的性能急剧下降,已经失去了判断主用户存在与否的能力。但是通过增大划分的子带个数,算法的计算复杂度会增加,需要在算法复杂度与性能之间平衡。设置信噪比为-12 dB,由图4可知,K值相同时,噪声不确定度为1 dB和没有噪声不确定度的曲线几乎重合,说明FD-CP-AC算法有较强的抗噪声不确定性能,可靠性强,能够克服噪声带来的严重影响。 图3 Pf=0.1、噪声不确定度为1 dB的情况下ED与FD-CP-AC算法性能 图4 -12 dB信噪比时FD-CP-AC算法性能 图5说明当虚警概率相同时,检测概率随信噪比的增加而增加,可以通过增大信噪比来提高算法性能。当K=512、虚警概率为0.1时,信噪比为-10 dB、-12 dB时的检测概率大于0.9,并且性能远优于能量检测算法。在算法应用过程中,可以根据实际信道的信噪比情况,将宽带划分为最佳的子带数,以实现该信噪比下的可靠检测。 图5 不同的信噪比下FD-CP-AC算法的性能曲线(1 dB噪声不确定度) 考虑宽带OFDM信号的频谱感知场景,双门限频域自相关算法仿真参数设置为:采用256正交振幅调制,IFFT点数为512,OFDM符号的有效子载波数为288,信号带宽为64 MHz,采样速率为128 MHz。 由图6可知,在相同信噪比下,当虚警概率相同时,双门限算法的检测概率高于单门限算法,性能较优越;当虚警概率趋于0时,单门限算法性能更好,但并不符合实际情况;当虚警概率为0.1时,单门限算法中只有信噪比为-10 dB、-12 dB时的检测概率大于0.9,但双门限算法在信噪比为-10 dB、-12 dB、-14 dB、-16 dB时的检测概率都大于0.9,满足实际应用中的性能要求,说明双门限算法能够进一步提高频域循环前缀自相关方法的频谱检测性能。 图6 双门限及单门限FD-CP-AC算法检测性能对比 由图7可知,Pf=0.1时,存在噪声不确定的情况下,能量检测算法的性能下降,已经丧失了频谱感知的能力。在相同的信噪比下,双门限频域自相关算法的检测性能都优于单门限算法。 图7 Pf=0.1时双门限及单门限算法检测性能对比 本文提出了基于循环前缀自相关的单门限及双门限频谱感知算法,进行了理论推导和仿真分析,验证了存在噪声不确定度时基于循环前缀自相关的频谱感知算法比能量检测算法具有更好的检测性能,能够有效地抵抗噪声不确定度对检测性能造成的影响,适用于复杂噪声环境低信噪比情况下的认知无线电系统。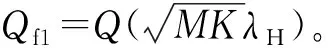
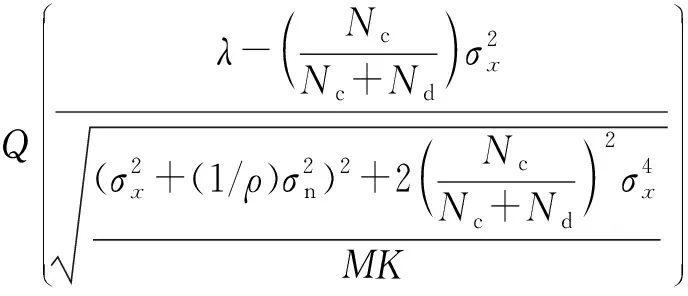
3 仿真与分析
3.1 单门限频域循环前缀自相关
3.2 双门限频域循环前缀自相关
4 结 论
