基于大别造山带电磁测深数据的磁暴感应地电场分布特性分析

2021-05-31王泽忠张廉杰倪政泽郭苏鑫

科学技术与工程 2021年12期

王泽忠，张廉杰，司远，倪政泽，郭苏鑫

(华北电力大学高电压与电磁兼容北京市重点实验室，北京 102206)

磁暴，即太阳活动引起的地球磁场剧烈变化。根据法拉第电磁感应定律，变化的地磁场会在地面感应出电场，进而在有接地系统的人工网络中产生电流，即地磁感应电流(geomagnetically induced currents, GIC)。GIC频率范围为10-4～10-2Hz，这种准直流电流会对人工网络及其配套设备的安全运行构成严重威胁[1-3]。因此，准确求解地磁扰动地电场成为防治地磁暴灾害的关键。

计算电网中GIC分为2个独立步骤：一是根据所需研究电网的地理位置建立大地电性结构模型，研究地磁扰动地电场的分布；二是根据电网结构参数建立等效直流模型，将地磁扰动地电场作为等效电压源施加在网络中计算GIC。与地上电网结构模型相比，由于大地的电性及其构造非常复杂，以及不同地区的差异大，建立准确的考虑大地电性及其构造差异的大地电阻率模型非常困难。文献[4-5]提出建立水平分层的大地电性结构模型，利用平面波法[6]结合地磁台测量得到的地磁场强度计算地磁扰动地电场。但是对于中国特高压长距离输电线路，其空间尺度达到几百甚至上千公里，所覆盖的区域包含多种地质构造。文献[7-8]将大范围区域分解为多个独立的一维结构，对于每一个小区域采用平面波法计算地磁扰动地电场，再将各个小区域拼接起来得到整个区域地磁扰动地电场。这种分区平面波算法没有考虑交界面处电导率突变对地电场的影响。文献[9-10]建立三维分层分区大地电性结构模型，使用有限元法计算地电场，采用自适应剖分时，网格数量多，所需内存大，计算速度慢。

由于确定磁暴感应地电场的数值是计算GIC的前提，磁暴感应地电场的计算又与大地电性特征有关，同时视电阻率又是在大地电磁测深法中用来描述地下电性分布特征的参数，因此引用了视电阻率参数来计算磁暴感应地电场。视电阻率的定义式中包含频率、磁导率、大地表面电场分量和磁场分量，通过大地电磁测深法实测得到的视电阻率数据是特定频率下的视电阻率数据，在磁导率已知的情况下，结合地磁台或地磁测量装置实测出的磁场数据，就可以简单、快速地计算出感应地电场数值。相较于复杂的大地电性结构三维模型建模，免去了大规模、高成本的计算，增加工程计算的经济性和灵活性，对研究磁暴感应地电场的计算和影响具有深远的意义。

1 电磁测深数据在磁暴感应地电场计算中的应用

在大地电磁测深法中引入了视电阻率的概念，以便综合反映大地层状介质的电性参数。大地电磁测深法的基本理论是建立在求解麦克斯韦方程组的基础上，考虑到大地电磁测深应用的观测频率范围及构成地壳浅部介质的电阻率范围，可忽略在大地介质中位移电流对场分布的影响，进而能够得到在谐变场情况下的电磁场波动方程，即亥姆霍兹方程[11]

∇2H-k2H=0

(1)

∇2E-k2E=0

(2)

为了研究大地电阻率和地面电磁场测量值之间的关系，引入波阻抗Z的概念，将其定义为电磁场水平分量之比，即

(3)

式(3)中：波阻抗Z的单位为Ω。

由于电磁场可以分成独立的2种波形，即TE模式极化波和TM模式极化波，所以可以获得2个正交测量轴上的波阻抗[12]：

(4)

(5)

式中：Zxy为TE模式下波阻抗；Zyx为TM模式下波阻抗；Ex和Ey分别为地电场南北分量和东西分量，Hx和Hy分别为地磁场南北分量和东西分量；ρ为电阻率。

在均匀各向同性介质中，由于电场和磁场之间是正交的，所以在地表上沿任意正交测量轴都有

(6)

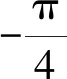
对于二维介质，电磁场可以沿电性主轴(如构造走向和倾向，电阻率分别为ρxy和ρyx)分解为2组相互独立的线性偏振波，这2组线性偏振波就如同分别在电阻率为ρxy和ρyx的均匀各向同性介质中传播，相应的波阻抗为

(7)

(8)

Zxy≠Zyx

(9)

当数据测量测量系统取X轴平行于构造走向，则Zxy=ZTE，即TE模式；Zyx=-ZTM，即TM模式。

在均匀各向同性介质中，通过式(6)，可以得到电阻率与波阻抗的关系

(10)

通过式(10)的电阻率与波阻抗的关系式进而引申得到了视电阻率的概念。

在均匀各向同性介质中，视电阻率的表达式为

(11)

即ρxy=ρyx。

式(11)中：ρs为电阻率；ρxy为TE模式下视电阻率；ρyx为TM模式下视电阻率。

在二维介质中，选取测量轴X平行于构造走向，则视电阻率可表示为

(12)

(13)

因此，每个大地电磁测点可以得到2条相应的视电阻率测深曲线。

通过视电阻率和波阻抗的定义式及其关系，可以看出电场与磁场在特定的频率下成比例关系，即在均匀各向同性介质中，有

(14)

(15)

在二维介质中有

(16)

(17)

通过上述关系式就可将计算感应电场的时域问题转换为频域问题，将多点求解问题转化为单点求解问题，即求解磁暴期间磁场在对应频域分量下的感应地电场频域分量。

2 数据来源

2.1 磁场数据来源

目前能收集到的磁暴数据有分钟级和秒级地磁场三分量(即地磁场总场F、偏磁角D和地磁水平分量H)数据。为了提高计算精度，文章选取秒级数据，求解地磁场的南北分量X和东西分量Y。

通过查阅资料获悉2004年11月7—9日期间发生了KP=8的急始类型的强磁暴，本次磁暴期间的变压器中性点电流幅度明显偏大。剔除因设备而导致的错误数据后，在大磁暴发生所在的2004年11月7—9日能够使用的数据包括黑龙江德都(DED)、广东广州(GZH)、甘肃嘉峪关(JYG)、新疆喀什(KSH)和乌鲁木齐(WMQ)、海南琼中(QGZ)、湖北武汉(WHN)7个地磁台站记录情况,7个台站地理位置信息如表1所示。

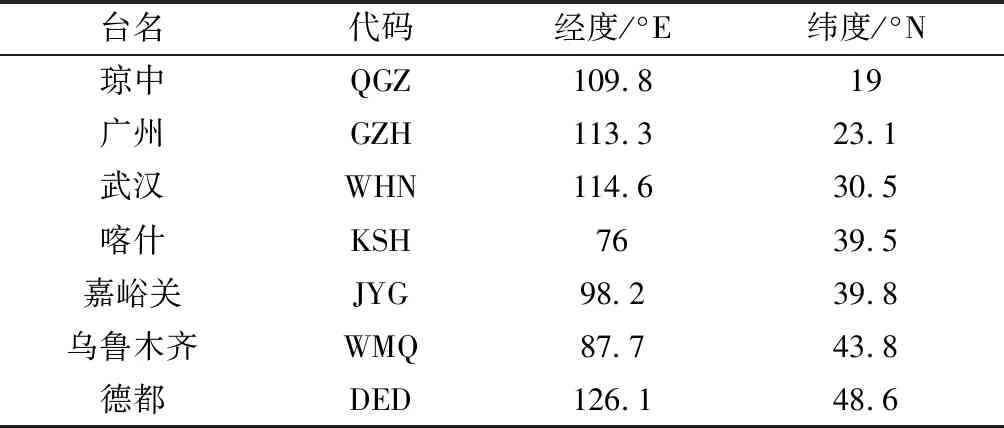
表1 地磁台站地理坐标

2.2 大地电磁测深数据的来源

选取的大别造山带大地电磁测深数据可由文献[13]中获得，该文献在大别造山带，由西往东布置了3条大地电磁测深剖面，剖面LA沿NE26°方向，共12个测点(LA1～LA12),长约153 km；剖面LB沿NE28°方向，共12个测点(LB1～LB12),长约167 km；剖面LC沿NE28°方向，共11个测点(LC1～LC11),长约173 km。3个剖面的测点分布情况如图1所示，这35个测点的大地电磁测深数据对磁暴感应地电场的计算及分析提供了数据依据。

图1 大别造山带大地电磁测深测点位置图Fig.1 Location map of magnetotelluric sounding points in the Dabie orogenic belt

3 数据选取与处理

3.1 磁暴期间磁场数据的选取与处理

为了提高计算的准确度和精度，根据选取同一纬度范围内，距离最近的地磁台站作为地磁场数据来源的准则，选取了与大别造山带纬度最接近、距离最短的武汉(WHN)地磁台站的秒级地磁场数据，求解地磁场的南北分量和东西分量。

在2004年11月7日18:28:08和9日18:50:23的磁暴急始时刻广东岭澳核电站内的变压器中性点电流峰值分别达到-47.2 A和-55.8 A(负号表示电流从大地流入中性点)。在9日22:50:35出现了更高的电流幅值，瞬时最大值达到75.5 A[14]，故选取以上3个时刻的地磁站磁场数据进行分析。

利用视电阻率数据进行磁暴感应地电场计算需在频域内进行，因此需对所选取的地磁场数据进行频谱分析。为了使频谱分析结果更加准确，可对磁场数据的时间区间作一定拓展，各时刻对应的地磁场数据起止时间如表2所示。

对拓展后的3段起止时间区间内的地磁场南北分量和东西分量进行FFT变换，得到的频域下磁感应强度南北分量和东西分量幅值结果如图2～图4所示。

表2 地磁场数据起止时间Table 2 Start and end time of geomagnetic data

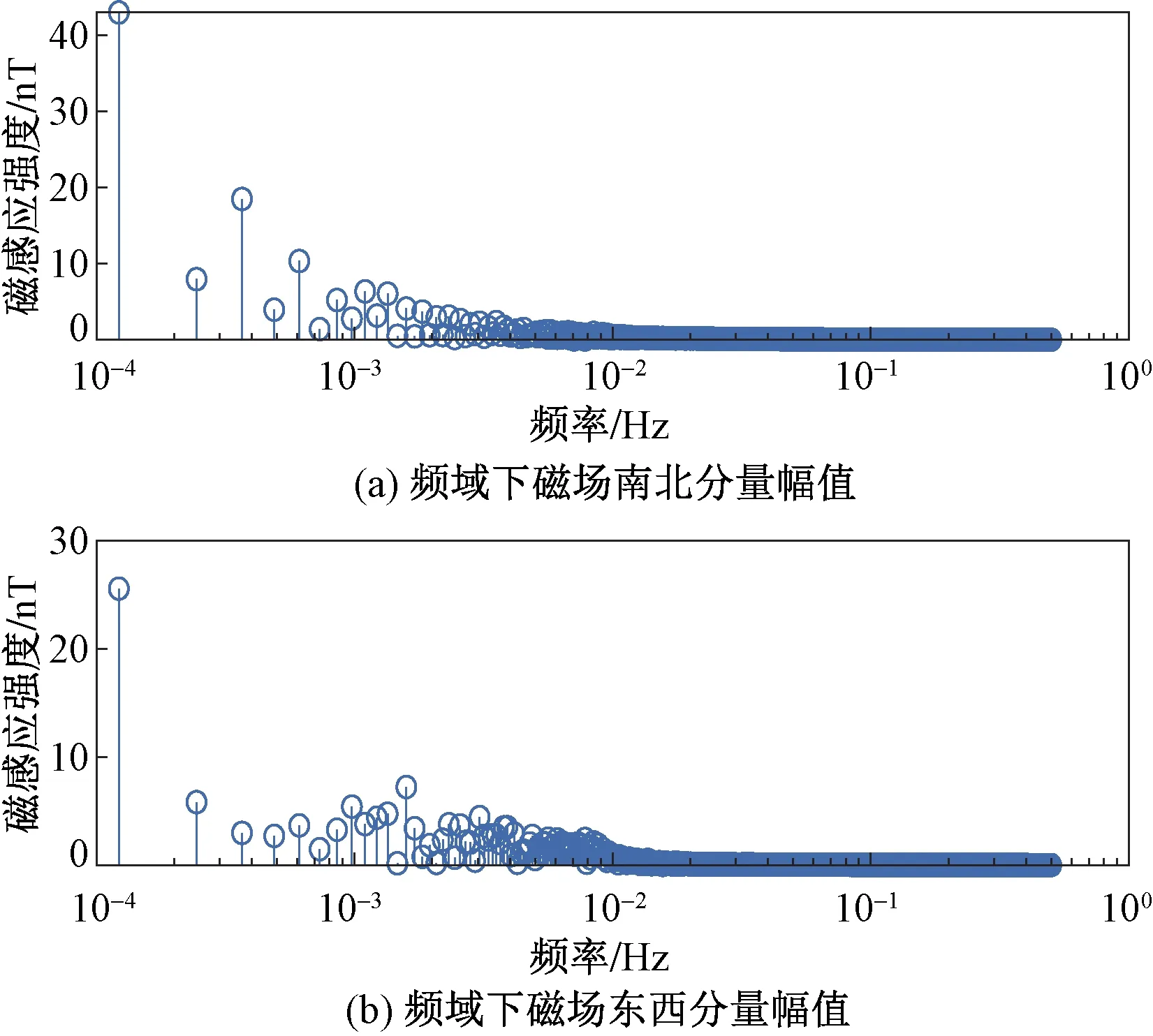
图2 第1段起止时间频域下磁场感应强度Fig.2 Magnetic field induction intensity in the frequency domain at the start and end times of the first segment

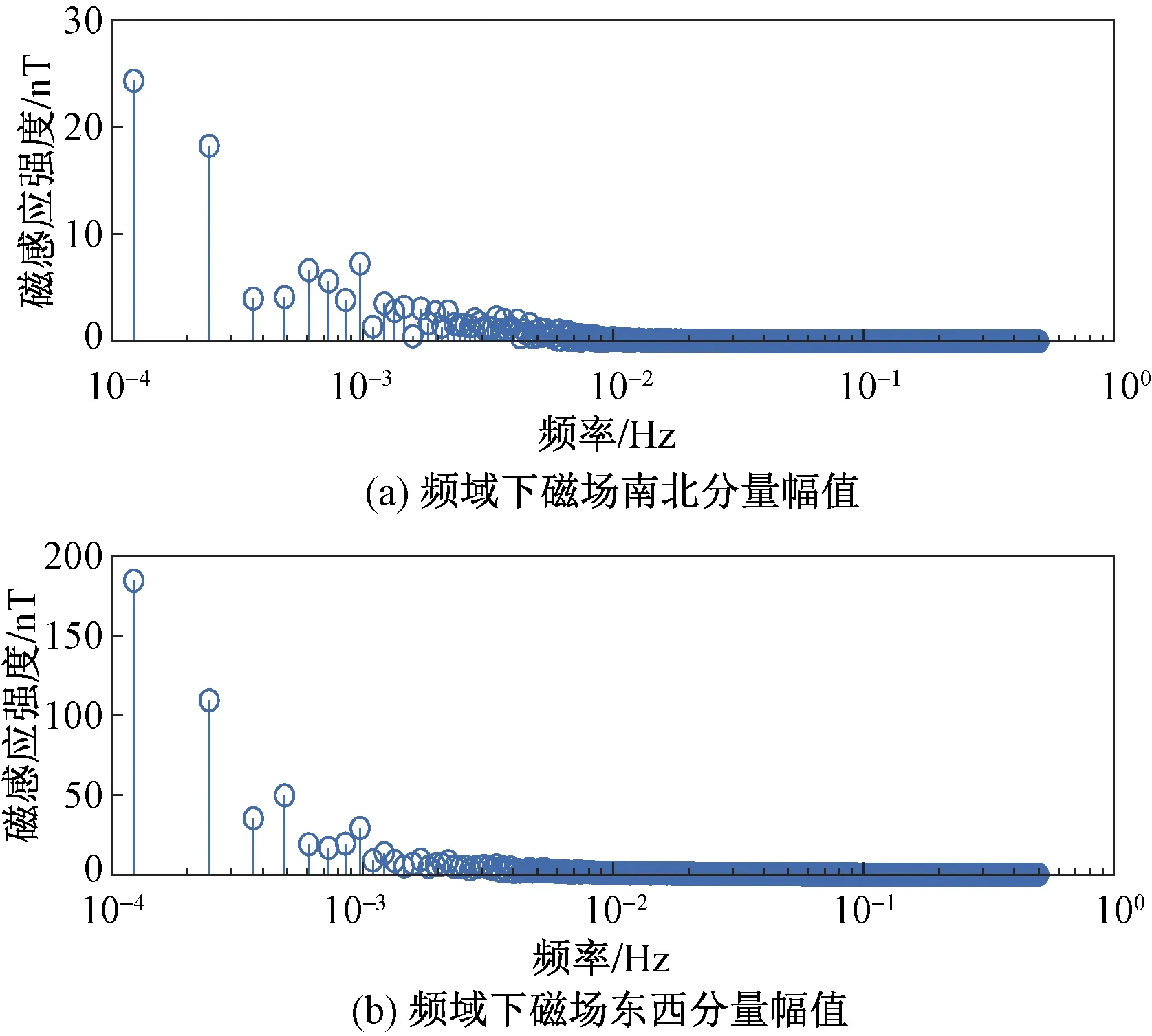
图3 第2段起止时间频域下磁场感应强度Fig.3 Magnetic field induction intensity in the frequency domain at the start and end times of the second segment

图4 第3段起止时间频域下磁场感应强度Fig.4 Magnetic field induction intensity in the frequency domain at the start and end times of the third segment

由图2～图4可以看出，所选取的地磁场数据的主要频率范围与GIC频率范围一致，即10-4～10-2Hz，同时对于10-2Hz以上的频率分量可忽略不计。因此，针对选取的3个起止时间段，若要在频域内进行高精度计算磁暴感应地电场，可只考虑10-2Hz以下的若干频率即可。

3.2 视电阻率数据的选取

由2.2节中对磁场数据进行频谱分析后得出的频率特性，可知基于视电阻率数据进行磁暴感应地电场计算时，通过10-4～10-2Hz范围内的视电阻数据即可进行磁暴感应地电场的频域计算。故选取了对应频率范围内的大别造山带3条剖面35个测点的视电阻率幅值数据进行频域计算，数据曲线如图5～图7所示。

图5 剖面LA视电阻率幅值曲线Fig.5 Curves of the apparent resistivity amplitude of the profile LA

图6 剖面LB视电阻率幅值曲线Fig.6 Curves of the apparent resistivity amplitude of the profile LB

图7 剖面LC视电阻率幅值曲线Fig.7 Curves of the apparent resistivity amplitude of the profile LC

图8 剖面LA频域电场强度幅值最大值计算结果Fig.8 Calculation result of the maximum electric field intensity in the frequency domain of the section LA

图9 剖面LB频域电场强度幅值最大值计算结果Fig.9 Calculation result of the maximum electric field intensity in the frequency domain of the section LB

图10 剖面LC频域电场强度幅值最大值计算结果Fig.10 Calculation result of the maximum electric field intensity in the frequency domain of the section LC

4 频域磁暴感应地电场计算及分布特性

4.1 频域磁暴感应地电场计算

基于10-4～10-2Hz频率范围内的大别造山带LA、LB和LC 3个剖面的实测视电阻率数据和磁暴期间3个起止时间段的武汉站(WHN)的地磁场数据，对上述35个测点进行磁暴感应地电场计算，分别得到每个测点在对应起止时间段内的频域感应地电场的电场强度南北分量幅值和东西分量幅值的最大值，以及对应的频率，计算结果如图8～图10所示。

4.2 磁暴感应地电场频域分量最大值分析

从图8～图10中(a)图、(c)图中磁暴感应地电场频域下电场强度南北分量幅值和东西分量幅值的计算结果能够明显地看出磁暴感应地电场频域分量最大值分布是很不均匀的。其中，磁暴感应地电场频域分量最大值介于2.189×10-4～2.719×10-1V/km，大小各不相同，主要电场强度频域分量最大值范围为10-3～10-2V/km。同时可以看出，第2、3段起止时间内都存在部分测点某一频率的电场强度幅值达到10-1V/km数量级的较大数值，需引起充分关注。

通过对比图8～图10中(a)图、(c)图，可以看出频域下电场强度的南北方向分量幅值最大值普遍大于东西方向分量幅值的最大值。

4.3 磁暴感应地电场频域分量最大值对应频率分析

通过图8～图10中(b)图、(d)图能够明显地看出，对于同一起止时间段内的磁暴感应地电场南北分量幅值、东西分量幅值的最大值基本分布在相同频率上，即磁暴感应地电场频域分量最大值对应频率在相同时间段内分布相对集中。其中，在第1、2段起止时间内的最大值频率集中分布在1.221×10-4Hz，第3段起始时间内的磁暴感应地电场频域分量最大值对应的频率集中分布在5.126×10-3Hz。此外，在2.441×10-4Hz和1.587×10-3Hz的频率上，也存在数量较多的电场强度频域分量最大值分布。对于以上频率下的电场强度，其频率数值较小，更加接近直流，而且分布相对集中，电场强度又是频域下该位置的最大值，可能对各种人工系统产生较大干扰，需引起足够重视。