压电复合材料中正六边形孔边裂纹反平面问题

徐 燕, 杨 娟

(1.宁夏大学新华学院， 银川 750021; 2.宁夏大学民族预科教育学院， 银川 750002; 3.宁夏大学数学统计学院， 银川 750021)

自1880年压电材料被发现具有压电效应以来，已经历了从自然界存在的简单单晶体材料发展到结构复杂的复合多功能材料的过程[1]。压电复合材料，就是由两相或多相材料按照一定的复合模式构成的一种具有压电性能的新型智能材料，它可以成倍地提高材料的压电性能。由于其良好的机-电耦合效应使得压电复合材料可用于制作信号处理器、转换器、传感器、驱动器等电子元器件，在航天航空、自动控制、生物医学等领域发挥着十分重要的作用[2]。

脆性的压电复合材料在加工和使用的过程中难免产生缺陷(如孔洞、缺口及裂纹)。因此，对于压电介质中含复杂缺陷断裂行为的研究从未间断[3-5]，尤其是压电复合材料中含有孔洞且孔边带有裂纹问题的研究成为近年来学者关注的一个热点问题。文献[6]求解了圆孔边裂纹的反平面问题。在电不可渗透和电可渗透边界条件下，文献[7]计算了椭圆孔边非对称裂纹尖端的应力强度因子。文献[8]确定了唇形裂纹在两种电边界条件下裂纹尖端场强度因子和机械应变能释放率的解析表达式。文献[9]对含光滑顶点的正三角形孔边裂纹的反平面问题进行了分析。文献[10]对翼形裂纹的反平面问题进行了研究。文献[11]研究了星形裂纹的断裂行为。在两种电边界条件下，文献[12]对正方形孔带四条裂纹的反平面问题进行了研究，并给出数值算例。文献[13]导出了力-电耦合作用下正三角形孔口裂纹以速度v传播时的动态应力强度因子和电位移强度因子的解析解。综上所述，尽管对于压电复合材料孔边裂纹问题的研究已取得不少的研究成果，但是，利用复变函数方法和Stroh公式研究压电复合材料中含正六边形孔边裂纹的反平面问题尚未见报道。现拟利用平面弹性复变函数方法和Stroh公式研究含有正六边形孔且孔边带裂纹的压电复合材料反平面断裂问题,深入地探索缺陷尖端的场强度因子和能量释放率与材料及其缺陷形状的内在联系，为工程力学分析提供了理论参考和依据。

1 压电复合材料孔边裂纹反平面问题的基本方程

针对横观各向同性压电复合材料，假设x3轴为极化方向，x1-x2平面为各向同性平面。根据文献[14],压电复合材料的反平面问题的本构方程可化简为

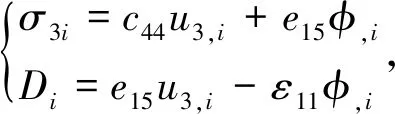
(1)

不计体力的力-电平衡方程

σ3i,i=0，Di,i=0，i=1,2

(2)

式中：重复指标表示求和；下标中逗号表示求偏导数；c44、e15和ε11分别表示压电复合材料的弹性常数、压电常数和介电常数；σ3i、u3、Di、φ分别表示应力、弹性位移、电位移和电势。

将式(1)代入式(2)，得压电复合材料二维反平面问题的最终控制方程为

B0∇2u=0

(3)

式(3)中：∇2是二维拉普拉斯算子，且广义位移向量和系数矩阵分别为

(4)

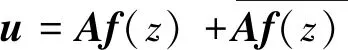
(5)

(6)

式中：f(x)为待定复势向量函数；材料系数矩阵B=iB0，且A=I为2×2的单位矩阵。

2 电不可通边界情况

2.1 力学模型

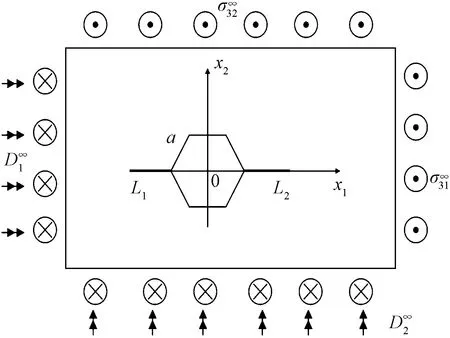
图1 无限大压电复合材料中正六边形孔边裂纹几何模型Fig.1 Geometric model for a crack near a regular hexagonal hole in infinite piezoelectric composites

在压电复合材料中，复势向量函数f(z)具有如下形式[16]：

f(z)=c∞z+f0(z)

(7)

式(7)中：c∞为与远场载荷条件有关的复常向量；f0(z)为未知的解析函数向量，在无穷远处取值为零，即f0(∞)=0。

对式(5)和式(6)两端关于x1求偏导数得

(8)

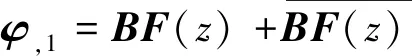
(9)

式中：F(z)=df(z)/dz。

将式(7)代入式(8)和式(9)，当z→∞时可得

(10)

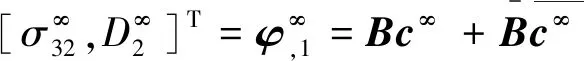
(11)

压电复合材料中正六边形孔边及其裂纹面上的力、电边界条件可表示为

(12)

式(12)中：t3、Dn分别代表沿边界所受的反平面剪切应力、法向电位移。

当裂纹内部的电场很小时，可采用电不可通边界条件，则式(12)可化为

(13)

将式(7)代入式(13)中，可得

(14)

为了便于求解以上边值问题，引入合适的保角映射[17]：

(15)

式(15)中：R为与正六边形边长相关的常数，由点的对应关系求得R≈0.925 8a，a为正六边形的边长。

通过式(15)共形映射原理(如图2所示)可以将正六边形外部区域保角映射到单位圆内部区域。对式(15),再令ζ=ζ-1，将单位圆内部映射变换到单位圆外部，获得正六边形外部区域到单位圆外部区域的共形映射，于是有

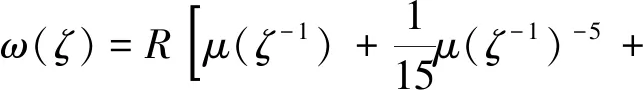
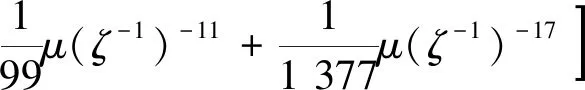
(16)

式(16)中：μ(ζ)为将圆孔边双裂纹外部区域变换到单位圆内部的共形映射函数[18]，即有

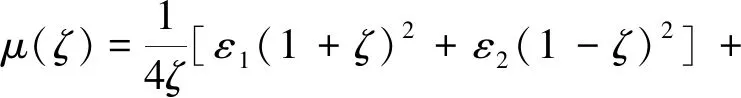
(17)

式(16)将z平面中的正六边形孔边双裂纹外部映射到ζ平面中的单位圆内部。其中ε为正实数，并且有

(18)

图2 保角映射原理图Fig.2 Conformal mapping schematic diagram

将式(17)代入式(16)并进行洛朗级数展开，可以获得ω(ζ)的前四项展开式为

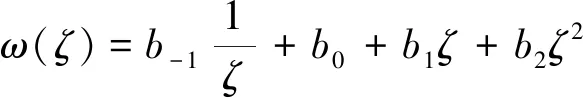
(19)

式(19)中：ω(ζ)洛朗级数展开式前四项系数分别为

在ζ平面上，式(14)可改写为

(20)

式(20)中：

(21)

(22)

因为f0(ζ)是在单位圆外解析的，所以f0(ζ)在单位圆内部是解析的，根据Cauchy积分公式，对于|ζ|<1内任一点ζ有

(23)

由式(19)可知，ω(ζ)在单位圆内除了一个一级极点ζ=0外是解析的，由留数定理可得式(23)右端的积分为

(24)

将式(24)代入式(23)，并对两端关于ζ求导，得

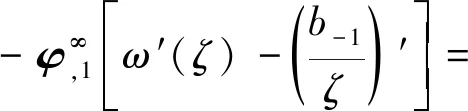
(25)

式(25)中：

(26)

2.2 场强度因子

定义裂纹尖端Ⅲ型场强度因子为[19]

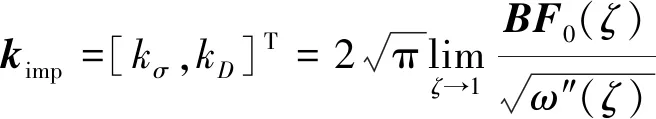
(27)

由式(25)可得

(ε1+ε2)+16(ε1-ε2)ζ}×

[2(ε1+ε2)2]-1

(28)

由式(26)可得

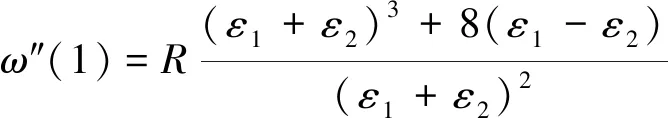
(29)

将式(28)和式(29)代入式(27)，再结合式(11)可得裂纹尖端的场强度因子表达式为

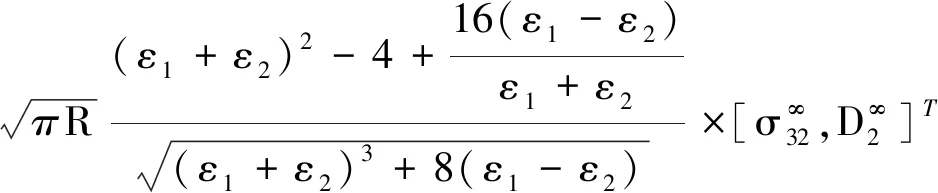
(30)

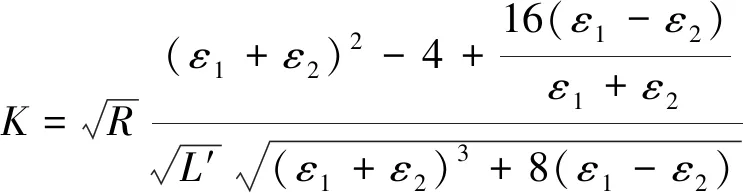
(31)

式(31)中：L′为裂纹的等效长度，L′=(L1+L2+2a)/2。

这与文献[20]中求解的无量纲场强度因子表达式一致。故由式(30)和式(31)，可得反平面问题正六边形孔边裂纹尖端的场强度因子的解析表达为

(32)

2.3 能量释放率

在电不可通边界条件下，根据文献[21]能量释放率的公式可定义为

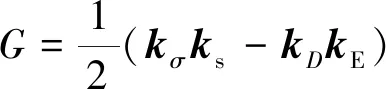
(33)

式(33)中：ks和kE分别表示应变强度因子和电场强度因子，可根据如下关系确定

(34)

将式(30)和式(34)代入(33)，并考虑到式(31)，得到裂纹尖端总能量释放率的表达式为

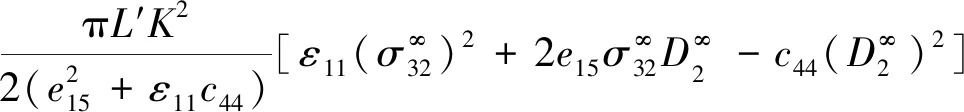
(35)

这与文献[12]中在电不可通边界下求解的能量释放率的表达式一致。

3 电可通边界情况

3.1 场强度因子

对于电可通边界条件可表示为

(36)

则得到电可通边界条件下场强度因子的解析表达式为

(37)

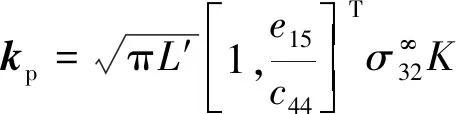
(38)

3.2 能量释放率

对于电可通边界条件下的能量释放率为

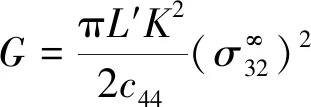
(39)

这与文献[12]中在电可通边界下求解的能量释放率的表达式一致。

4 数值算例

本文以压电陶瓷材料PHT-5H为例，根据文献[22]知其弹性常数、压电常数、介电常数、临界能量释放率分别为c44=3.53×1010N/m2，e15=17 C/m2，ε11=1.51×10-8C/(V·m)，Gr=5.0 N/m。图3给出了等效场强度因子K随着左裂纹L1/a的变化曲线。从图3很容易看到，等效场强度因子随着左裂纹长度的增大而增大，然后趋于一个定值。并且当左裂纹的长度一定时，左尖端的等效场强度因子随着右裂纹的增大反而减小。这说明左裂纹促进裂纹的扩展，右裂纹抑制左裂纹的扩展。

图4给出了等效场强度因子K随孔口边长a/L2的变化曲线。从图4可以看出等效场强度因子随孔口边长的增加而增加，先急剧增长然后趋于一个常数，这表明裂纹扩展到一定程度时孔口边长对等效场强度因子的影响较小。另外，在边长一定的情况下，等效场强度因子随着左裂纹增大而增大。

图5给出了在电不可通和电可通两种边界条件下，能量释放率G/Gr随L1/a的变化曲线。从图5可以观察到，在电不可通和电可通两种边界条件下，当孔口边长和右裂纹长度固定时，能量释放率随左裂纹长度的增加而增加；在同一边界条件下，当左裂纹长度给定时，右裂纹长度越长，对应的能量释放率反而越小。另外，在相同条件下，电可通边界条件的能量释放率比电不可通边界条件下的能量释放率稍大一点。

图6给出了在电不可通和电可通边界条件下，能量释放率G/Gr随a/L1的变化曲线。从图6可以看到，在电不可通和电可通两种边界条件下，当左、右裂纹长度固定时，能量释放率随孔口边长的增大而增大；在同一边界条件下，当孔口边长给定时，左裂纹长度越长，对应的能量释放率越大。另外，在相同条件下，电可通边界条件的能量释放率比电不可通边界条件下的能量释放率大一些。

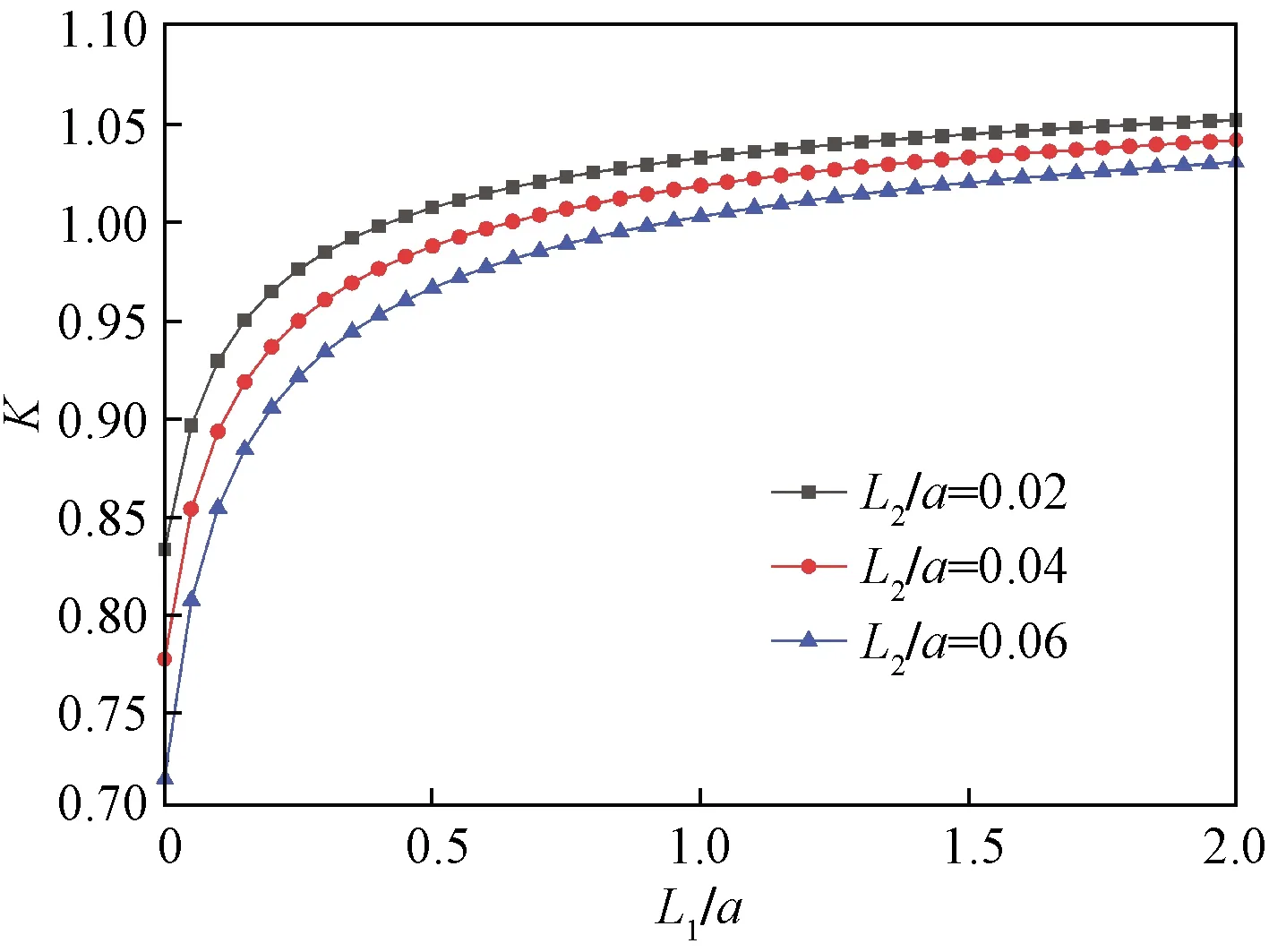
图3 等效场强度因子K随L1/a的变化关系Fig.3 Variation ofK with L1/a

图4 等效场强度因子K随a/L2的变化关系Fig.4 Variation of Kwith a/L2

图5 能量释放率G/Gr随L1/a的变化关系 Fig.5 Variation ofG/Grwith L1/a

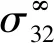
图6 能量释放率G/Gr随a/L1的变化关系Fig.6 Variation ofG/Grwith a/L1

图7 能量释放率G/Gr随 的变化关系Fig.7 Variation ofG/Grwith

图8 能量释放率G/Gr随的变化关系Fig.8 Variation ofG/Grwith

5 结论

基于解析函数边值理论，运用广义复变函数方法和Stroh公式研究了压电复合材料中正六边形孔边裂纹反平面问题。结合压电复合材料面内应力、电位移的复势表示及边界条件，将压电复合材料力学问题转化为边值问题。通过引入一个合适的广义保角变换和逆变换，充分利用柯西积分公式和留数定理等工具推导得到缺陷尖端的应力、电位移强度因子以及能量释放率的显示表达式。数值算例分析了几何参数、裂纹尺寸及力电载荷对等效场强度因子的影响，并探讨了在电不可通和电可通边界条件下能量释放率随孔口边长、裂纹尺寸及机械载荷、电载荷的变化规律。结论揭示了压电复合材料在受到外载荷时破坏的机理，为压电复合材料及元器件的制备、设计和应用提供理论基础及科学依据。