浅谈课堂教学中学生的局限性发展

顾燕琪

（江苏省昆山高新区美陆小学 江苏昆山 215300）

11月底听了一年级的“6、5、4、3、2加几”一课，上课老师的板书是课题下面写了“凑十法和联想法”，很明显，本课的重点是突出了凑十法和联想法的计算方法。教学难点是让学生会运用这两种方法正确计算20以内进位的加法。整节课，教师的重难点突出，条理清晰，层次分明，练习形式多样，学生计算的题量也较多，每个环节都处理得很到位。通过课堂教学，学生能够正确地计算20以内进位的加法算式，完成了本课的教学目标。放大视角，将这节课放回整个单元中，登高望远。学生的语言表达能力真正地发展了吗？思维能力真正地提高了吗？基础知识真正掌握牢固了吗？让我有了新的想法。

一、局限学生语言的完整性表达

[片段1]在例题教学“6+5”时，上课老师的多媒体课件上出示：

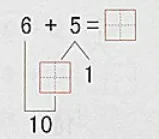
师：我们可以用之前学过的什么方法进行计算？

生：凑十法

师：你能填一填吗？

生：填一填

师：能说一说吗？多媒体课件上出示：

生：……

[片段2]

师：3+8怎么计算？

生：我想8+3=11。

师：那么3+8就等于？

生：11.

师：为什么？

生：指着黑板上的板贴：联想法。

……

通过教师的教学，学生能运用所学的方法正确计算。但不难看出，学生的数学语言能力得到发展了吗？在片段1中，学生照着样子完整地说计算过程，学生是真正地能完整地表达？何况“凑十法”三句式表达不是本课的新知，如果教师让学生看着算式，主动完整地表达6+5的凑十法过程，学生的语言表达能力才能够得到发展。在片段2中，教师的这种提问，让学生“只知其一，不知其二”，即知道用的计算方法是“联想法”，却不知道联想法是什么方法，这时，教师要再问下去：也就是什么方法？要让学生完整地表达出“交换加数的位置，和不变”就是联想法的方法。在两个片段中，教师注重教法，侧重计算的正确结果，却忽略了学生的学法，忽略了学生对计算过程的完整性描述，局限了学生语言的完整性表达。因此，在课堂教学中，教师要准确地把握教材的知识内容，提高提问的有效性，使学生的语言发展不再受到局限。

二、局限学生思维的连续性发展

[片段3]出示：4+9

师：你是怎么计算的？得数是多少？

生：凑十法

师：怎么凑的？

生：把4分成3和1，1加9凑成10，3加10等于13。

师：为什么4要分成3和1呢？

生：4的后面是9，4里面分出1来才能与9凑成10。

师：说得真好。还可以怎么想呢？

生：计算4+9，可以想9+4。

师：怎么想9+4呢？

生：把4分成1和3，1和9凑成10，10加3等于13。

师：这种交换加数的位置，和不变，我们叫什么？

生：联想法。

……

课堂上，经过老师的连续提问和引导，学生能运用“凑十法”和“联想法”计算出4+9的得数。然而，这节课的教学内容是建立在“9加几”“8、7加几”的基础上学习的。凑十法是“9加几”中学生学习的一种计算方法，联想法是“8、7加几”中学生学习的又一种计算方法。我认为，今天的课堂教学中，并不是两种计算方法的教学再现，灵活地运用是重点。在计算“4+9”时，首先，让学生讨论：运用什么方法可以直接得出结果，能又对又快地算出？接着小组交流，得出：运用凑十法能计算4+9等于13，也可以运用联想法能计算4+9等于13，通过比较，运用联想法，计算4+9等于13的速度更快一些。然后，让学生明确：我们已经学过了9+4，运用了凑十法能很快地说出得数了，那么现在计算4+9，你能很快地直接说出得数吗？最后，让学生练习1：算一算：3+9、2+9、3+8、4+8：；练习2：找一找。学生自己找能运用这种方法直接计算的几加几。

在课堂中，学生在老师的指向性引导下，对“凑十法”和“联想法”的运用能力得到了充分的发展，老师训练得很到位。纵观全单元，学生的思维在这节课中出现了片段性的重复性的发展。学生已经掌握了运算方法，为什么不让学生去灵活地运用呢？为什么不让学生自己体会比较呢？学生的思维是连贯的，今天的课堂，是学生连续性发展、递增性的发展的最佳平台。通过比较，学生的计算思维不局限在方法同等的水平上，体会了“联想法”的计算优势，既快速又方便，学生的思维发展提高了。通过“算一算”“找一找”的练习，使学生的计算方法上升到了直接口答这高一级的计算目标，学生的思维发展连续性了。所以，在课堂教学中，教师不能局限学生的思维发展，要“大处着眼，小处入手”，不仅要关注学生知识能力的发展，还要关注学生思维的连续性发展，触动学生的思维神经，促使其在不断的练习中得到延伸和发展。

三、局限学生知识的系统性构建

教师将教科书上的习题一一练习结束后，又增加了青蛙跳伞等游戏互动的环节，可以说学生的计算练习量达到了教学目标，计算的能力得到了更进一步的提高，课堂的最后，学生的积极性也调动了起来，激发了学生的学习兴趣。但从知识纵向看，学生掌握的知识局限在本课的习题上，只是单一地完成每道练习题，如果在课堂练习的同时，首先，让学生将计算的习题分类，明确新旧知的内容，如例题教学时，6+5、5+6是新知，试一试4+9、3+9、2+9通过联想法计算可以说不是新知。在课堂的总结练习中，教师有序地罗列本课计算过的算式，学生再填补20以内进位加中没有计算到的算式，形成一张本单元的进位加的算式表：

9+2 8+3 7+4 6+5 5+6 4+7 3+8 2+9

9+3 8+4 7+5 6+6 5+7 4+8 3+9

9+4 8+5 7+6 6+7 5+8 4+9

......

9+9

最后，让学生完整地诵读加法算式表，找出表中的规律，激发学生直接说出得数的积极性。在这样的课堂教学中，算式的分类与罗列，是对计算题进行完整化，既见树木，又见森林。有序地排列和找规律，是对进位加法这一单元知识进行系统化。学生诵读计算表，对这个单元的加法算式进行了整理，形成自有的加法计算网，上升到一定的系统层面时，对计算的知识认知不再片面化。由单一知识到整体知识的学习型课堂教学，通过教师的放大、点燃，学生获得了学习进位加的基本性理解，打破了整体知识构建的局限性，完善建构了系统性知识。

课堂教学好比“一叶落知天下秋”，虽是短短的一节课，却是整个单元的点点星光；虽是处处的思维碰撞，却是学生成长的滴滴雨露。要让学生的学习不受局限，教师先要打破自身的种种“局限”。在平时，我们不仅要关注学生语言能力的表达，更要关注学生语言能力的完整性表达；不仅要关注学生思维能力的发展，更要关注学生思维能力的连续性发展；不仅要关注学生基础知识的掌握，更要关注学生基础知识的系统掌握。要让学生站得高，教师绝不能站得“矮”。教师钻研好教材，备好课，才能上好课。教师把握好全局，运筹帷幄，学生才能上好课。