基于耦合过程的抽水含水层压缩线性预测方法研究

2021-05-31吕伟华杨帅辛文青孙信张继周薄冠中

林业工程学报 2021年3期

吕伟华，杨帅，辛文青,孙信，张继周，薄冠中

(1. 南京林业大学土木工程学院，南京 210037；2. 水能资源利用关键技术湖南省重点实验室，长沙 410014；3. 公路地质灾害防治工程技术研究中心，银川 750004；4. 中交一公局第二工程有限公司，江苏苏州 215011；5. 江苏交通控股有限公司，南京 210016)

地面沉降已成为我国各大城市的主要工程地质问题之一。其中，上海最大沉降中心已达2.6 m多，沉降超过2 m的城市还有天津、太原、西安等，苏锡常地区最大沉降中心甚至达到2.8 m。国际上如墨西哥、日本和美国等国家的很多城市也都存在严重的地面沉降问题[1]。地下水的过量开采是引发地面沉降问题的最主要因素，而含水层的压缩变形量不可忽略[2-3]。因此，如何科学评估含水层压密变形是抽水地面沉降问题研究的重要课题之一。

开采地下水引起地下水位下降，地层的有效应力增加进而发生压密变形，从而导致地面沉降发生[4-7]。但地质条件的复杂性和差异性、地下水位波动以及地表荷载作用使得要准确预测地面沉降非常困难。依靠抽水地面沉降实测数据统计规律进行预测分析是一种可靠的有效研究方法[8-9]，在基坑工程中也常根据降水实测统计数据资料对含水层的变形特性进行规律分析[10-13]，但这类方法往往需要长期观测且易忽略土性本质；当采用不同概化模型数值计算分析进行地面沉降的预测[14-16]时，虽然参数选择容易但合理性不易满足，结果的可靠性难以令人信服。

本研究采用设计模型箱模拟含水层弱透水层交替地层系统，研究特定抽水控制条件下的含水层压缩特性，通过水位降深与含水层变形的规律分析，建立基于水力坡降含水层压密孔隙变化的耦合关系，针对地面沉降中含水层的变形规律进行趋势预测。

1 模型试验与结果

模型箱如图1所示，侧面为矩形，尺寸为60 cm×50 cm×100 cm，选用高强有机玻璃板和三角钢条焊接加固，不考虑侧向变形。槽内壁均匀涂抹凡士林作隔水边界。含水层选用长江底清淤砂，弱透水层选用亚黏土，物理性质见表1，颗粒分析见图2。如图1所示，以PVC管在模型中心处模拟抽水井对底部含水层非完整井式抽水，底边10 cm设进水口，纱布包扎以防堵塞，管壁与土层间隔套管允许自由滑动但不透水；通过槽侧壁钻孔，于含水层内部较低位置处设细水位管并定时开阀测水头，在各层位交界处分别铺设沉降板。模型填筑完成后沿抽水管慢速回注61 kg地下水，至填筑体顶面水体浸润，覆盖保护层以防水分散失。

图1 模型槽试验Fig. 1 Layout of the physical model of aquifer systems

表1 含水层系统填土物理性质参数Table 1 Physical property parameters of tested soil in aquifer system

图2 砂土、黏土颗粒分析曲线Fig. 2 Particle size distribution of sand and clay

采用虹吸原理从含水层系统埋设的模拟抽水井中以定速/定量按一定间隔时间分级抽水，并将抽出的水密封保存，待整个系统最终沉降稳定后，按原方式全部注水回灌。完整的抽水注水时程曲线如图3所示，为了让试验系统中的土层因释水发生的缓慢变形得以充分发展，分级抽水的间隔时间较长。含水层的变形-水位降深-历时曲线如图4中黑色散点球所示，各坐标平面投影线为相对变化关系曲线。

图3 抽水、注水时程曲线Fig. 3 Distribution of dewatering and recharging

图4 抽水含水层变形-水位降深-历时曲线Fig. 4 Diachronic curve of the pumped aquifer-water level dropdown

很明显，抽水期结束后含水层的变形仍发生了缓慢增长。参考文献[16]所用的统计方法，模型试验所得的水位降深与抽水层的压缩变形满足双线性关系，其斜率可以用来确定抽水含水层的储水系数。因此，将抽水期的含水层变形进行拟合归一得到如图5所示的含水压缩层累计变形时间半对数曲线。根据Cooper-Jacob半对数直线方法[17]有：

(1)

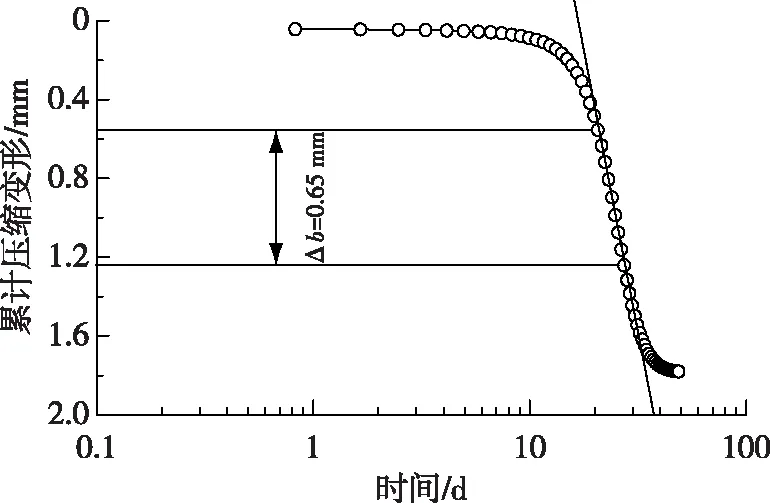
图5 压缩变形-时间半对数拟合曲线Fig. 5 Fitting curves between compression deformation versus time semi logarithmic

式中：s为某时段t所对应的水位降深，m；q为抽水井抽水速率，m3/d；T为含水层的导水系数，m2/d；r为与抽水井的距离，m；Ss为承压含水层储水系数，无量纲。

在短时间t1～t2之间水位降深Δs可表示为：

(2)

对于一维固结问题，含水层储水系数即为：

(3)

式中：Δb为含水层的变形量，m；Δh为抽水层的水位降深，m。抽水含水层的储水系数可表示为：

(4)

如图6所示，基于抽水期含水层水位降深与压缩变形统计后明显满足双线性关系，即达到临界水位降深时有效应力为含水层砂土层前期固结压力。据前期固结压力后的水位降深压缩变形斜率即可得到抽水含水层储水系数值。表2所示分别为采用Cooper-Jacob法、双线法得到的抽水含水层储水系数与薛禹群[18]、Marsily[19]所给参考值的比较，就系数量级而言，可认定本次模型试验得到的抽水含水层储水系数基本合理，模型试验是有效的。

图6 水位降深-压缩变形曲线Fig. 6 Curves between water level dropdown and compression deformation

表2 含水层储水系数计算对比Table 2 Calculation and comparison of water storage coefficient of pumped aquifers

2 考虑耦合过程的含水层变形

基于大量砂土渗透试验的数据统计及规律分析，Lambe等[20]给出了初始孔隙比为e0的含水砂层渗透系数与孔隙比之间存在如下经验关系：

(5)

式中：e为孔隙比，无量纲；k0为初始孔隙比为e0时的渗透系数，cm/s；k为孔隙比为e时的渗透系数，cm/s。

考虑一维流固耦合过程是基于渗流特性与固结条件关系的联合作用，即可通过含水层储水系数与砂土的压缩性指标之间建立定量联系实现。鉴于含水层的抽水与回灌从力学机制角度理解为对含水层的加载与卸载，其实质相当于在e-lgp曲线中水位降深引起含水层有效应力的增加从而导致抽水含水层砂颗粒间的压密变形，而压密后的含水砂层空隙比减少，反映了抽水水位降深的作用影响效果。令cc为超过前期固结压力后的压缩指数，建立水头高度与孔隙比的关系式如下：

cc(lgh-lgh0)=e0-e

(6)

式中：h为对应孔隙比为e时的水位降深，m；h0为初始状态孔隙比为e0时的水位降深初值，m。根据式(6)可以得到：

e=e0-cclg(h/h0)

(7)

将式(7)代入式(5)并乘以含水层厚度H可得到其导水系数表达式：

T(h)=Hk0[1-cclg(h/h0)/e0]3×

{1+e0/[e0-cclg(h/h0)]}

(8)

为实现对超过含水层前期固结压力后的水位降深的简化计算，将公式(8)基于数值计算方法就水位降深与导水系数间的定量关系进行线性等效，可得到如图7所示的直线表达式：

T(h)=Ah+B

(9)

图7 导水系数与水位降深关系简化Fig. 7 The simplified relationship between water conductivity coefficient and water level dropdown

式中，A、B为考虑抽水含水层初始状态、压缩性、抽水水位降深关系的常系数，无量纲。

将式(9)代入式(1)，含水层抽水引起的渗流与竖向变形过程耦合，反映了孔隙的减小与渗透性减弱同步发展过程，得到抽水含水层计算的水位降深表达式为：

(10)

根据Newton迭代法，先构造一个迭代函数代替原方程进行求根计算，而后得到新的求解迭代格式，取某一个时刻t0的初始水位h0进行迭代试算，至任一时刻ti的水位降深为hi，直至迭代计算误差限ε(如可取为0.001)满足要求即止，满足收敛性要求。

其中，某计算时刻的水位降深迭代解计算式合理数值解的表达式如下：

(11)

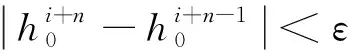
(12)

该方程对抽水含水层压密变形计算是基于水位降深表达式(11)的迭代，即反映了简单一维条件下水头变化的渗流与固结变形的耦合过程。通过模型试验实测数据分析所得的含水层物理力学和抽水指标参数(表3)，对该计算方法进行合理性验证。对比结果如图8所示，明显可知考虑耦合过程的计算结果较非耦合值与实测结果更加接近。

表3 抽水含水层计算参数Table 3 Calculation parameters of pumped aquifer

图8 含水层变形-水位降深-历时曲线对比Fig. 8 Comparison between calculated results and monitored data of aquifer deformation-water level dropdown-diachronic curves

作为苏锡常地区地下水主采层，第Ⅱ承压水水位动态完全受开采控制。从开采层次看，区内地下水以第Ⅱ承压水为主，据统计该层内开采井共2 978 眼，占总井数的70.28%，年开采量约2.2×108m3，占总开采量的65.42%，主要分布在沪宁线两侧，平均单井开采量约为1 000～2 500 m3/d。为进一步验证上述方法合理性，选取常州清凉小学抽水水位降深、地面沉降历时监测数据进行计算对比，所选计算参数如表4所示。

表4 原位含水层计算所取参数Table 4 Calculation parameters of pumped aquifer in situ

含水层水位降深和累计压缩变形如图9和图10所示。由图可见，发生的水位降深与累计压缩变形的非耦合计算值与耦合计算值都较实测值偏大，但后者更接近实测结果，显然更合理。与模型试验相比，清凉小学的水位降深-压缩变形的双线性关系此处未见，仅呈现单向趋势规律发展，原因是该处地下含水层系统已经历长期抽水水位降深累积作用，即水位降深值早已超过前期固结压力。综上分析，本研究方法可为后续提出一种含水层压缩量评估的预测方法提供基础。

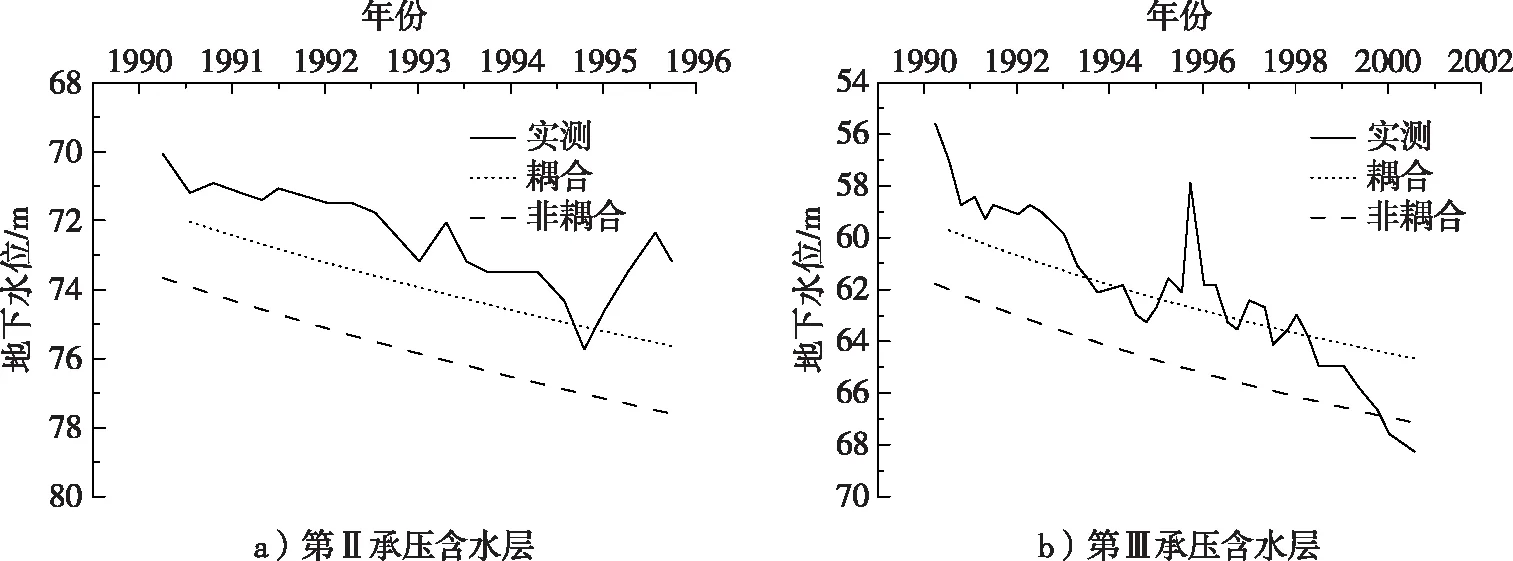
图9 含水层水位降深历时曲线计算对比Fig. 9 Comparison between water level drawdown-diachronic curve of pumped aquifer

图10 含水层累计压缩变形历时曲线计算对比Fig. 10 Comparison between cumulative compression deformation-diachronic curve of pumped aquifer

3 地面沉降预测方法

抽水含水层的水位降深本质上可等效为对砂颗粒骨架的加载，含水砂层颗粒间孔隙被挤压而体积缩小，整个土层发生压缩变形，其渗透水能力将减弱。为考察水位降深对含水砂层渗透系数影响敏感性，设计一组理想计算模型试验。基于公式(10)，令含水层中某一抽水井的抽水量q=45 m3/d，含水层平均厚度H=100 m，其储水系数设为常数Ss=10-5，初始孔隙比为e0=0.756，当抽水时间为365 d时，渗透系数从8.8×10-4cm/s变化为1.2×10-5cm/s，导水系数从76 m2/d变化为1.0 m2/d，发生水位降深37.25 m。

距抽水井r=50 m处，水位降深、渗透系数随抽水时间变化关系如图11所示。以某一速率抽水，水位降深随时间不断增加，而降深较小的初段渗透系数减小显著，当超过某水位降深后，其变化不是很明显。图12所示为理想抽水试验模型的含水层压缩变形、水位降深受抽水量影响的关系曲线。

图11 理想计算模型变化曲线Fig. 11 Change curve of ideal calculation model and results

抽水是引起地面沉降的根本原因，因此基于沉降随抽水量的发展变化规律，通过如图13所示控制抽水速率和抽水时间从而限制总抽水量以达到控制地面沉降的目的。

图13 抽水地面沉降预测方法Fig. 13 Prediction method of land subsidence

基于上述研究对常州清凉小学第Ⅲ承压含水层进行实例分析，所选计算参数同上。基于实测值预测、非耦合计算预测与耦合计算预测结果3部分组成的对比情况见图14，实线部分为已知的统计数据，虚线部分为预测。如果仍按2000年结束时的抽水速率，而不采取控制开采地下水量的措施，则至2010年左右，第Ⅲ承压含水层的实际水位将降深至70 m，考虑耦合的计算预测为70.8 m，而不考虑耦合的计算预测水位则达到73.5 m；同理，至2010年，该含水层发生的累计压缩变形根据实测数据预测为163.2 mm，根据耦合计算值预计将达到191 mm，而非耦合计算结果预测为223.9 mm。