含电学边界的压电层合梁的非线性弯曲波1)

赵希宁 杨晓东 张 伟

(北京工业大学机械结构非线性振动与强度北京市重点实验室,北京 100124)

引言

在工程实际与科学实践中都存在大量的非线性因素,其中很多因素都可归纳为非线性波问题,因此对非线性弹性波理论的研究有着重要的理论和实际意义[1-2].孤立波和冲击波现象的研究最早可以追溯到1834 年,英国科学家Russell 偶然发现了一种在行进的过程中波形和速度没有明显变化的波,并称这种波为孤立波[3].1895 年,Korteweg 等[4]在研究浅水波的运动时,得到了能产生孤立波的浅水运动的非线性方程,并求得了孤立波解,首次证实了孤立波的存在.1965 年,Zabusky 和Kruskal[5]运用仿真手段研究了两个孤立波的碰撞特性,发现孤立波在碰撞前后,波形特性不发生变化,说明了非线性理论中不存在线性叠加原理.1970 年,Taylor 等[6]解释了没有色散项只有非线性项的孤立波现象,证明了只有非线性项的孤立波波形比较尖陡,而加入色散项后孤立波的波形变得平缓.1980 年,国内朱位秋[7]研究了弹性杆中非线性波的传播行为[7].

21 世纪以来,科学家们推导出了固体中非线性演化方程的孤立波解和冲击波解[8-12].Duan 等[13]基于非线性弹性杆的纵波运动方程,利用摄动理论证明了非线性弹性杆中存在孤立子.Parkes 等[14]利用雅可比椭圆函数展开法构造并求解了非线性波动方程的精确周期解.研究表明,用该方法可以得到许多新的周期解,且在其极限条件下可以得到更多的激波解或孤立波解.Dai 等[15-16]分别研究了可压缩和不可压缩杆中的非线性波传播问题,导出了一类新的非线性色散方程,证明了这两类系统中存在冲击波、孤立波、周期冲击波等.Zhang 和Liu[17-20]在考虑有限变形、黏性效应和横向惯性的影响时,得到了弹性圆柱壳和杆的非线性薛定谔方程,证明了孤立解和激波解的存在.Xue 等[21-22]建立了磁电弹杆的非线性波动方程,并通过雅可比椭圆函数展开法进行求解,结果表明在磁电弹杆存在孤立波.Bulut 等[23]建立了磁电弹杆的非线性纵波方程,并运用sinh-Gordon 展开法对其求解,得到了拓扑孤子解、非拓扑孤子解和奇异孤子解.Lpbal 等[24]研究了含有泊松效应的弹性杆中的非线性纵波扩散问题.

除了对弹性杆非线性纵波的研究之外,对梁结构非线性弯曲波的研究也取得了很多进展[25-28].Zhang 等[29-30]考虑了横向、轴向和旋转惯性效应,导出了大挠曲梁的非线性波动方程,得到了孤立波解和冲击波解.Wei 等[31]建立了压电层合梁的弯曲波方程,利用拓展的F-展开法和约化摄动法得到了冲击波解、孤立波解以及亮孤子和暗孤子解.然而,到目前为止,关于压电耦合效应以及电学边界条件下压电层合梁模型非线性弯曲波的研究还没有报道.

本文提出了含有电学边界条件的无限长压电层合梁模型,研究了非线性弯曲波的传播问题.首先,考虑梁的大挠度引起的几何非线性效应、压电耦合效应和电学边界条件,利用欧拉−拉格朗日方法建立了无限长矩形压电层合梁弯曲波的非线性模型.其次,采用椭圆函数展开法对非线性弯曲波方程进行求解,得到了非线性弯曲波动方程的精确周期解及在极限情况下对应的冲击波解和孤波解.最后,利用约化摄动法得到了非线性薛定谔方程,进一步得到了亮孤子和暗孤子解,且具体研究了外加电压、压电层厚度等参数对冲击波、孤立波以及孤子特性的影响.

1 压电层合梁模型建立

图1 给出了矩形压电层合梁的简化几何模型,压电层合梁由均匀压电材料和基体材料组成,梁的横截面在变形前后均保持平面.不考虑泊松效应,以x方向为轴向方向,z轴为弯曲变形方向,其他两个方向梁不受任何力.基体厚度hs,压电材料厚度hp,基体梁和压电层的宽度都是b.压电层合梁上表面压电层的极化方向沿z轴正方向,受到电势V作用,下表面压电层的极化方向与上表面相反,沿z轴负方向,下表面压电层接地且电势为0,压电层合梁的振动方向沿厚度方向.

图1 矩形压电层合梁的示意图Fig.1 Schematic of the rectangular piezoelectric laminated beam

取梁变形前的轴为x轴,梁发生横向弯曲的方向与中性面垂直,在x方向没有外力作用的情况下,可以采用下列位移表达式

式中W为z方向的挠度,考虑有限挠度的情况下,梁截面上任意点处的应变可以表示为

基体梁和压电层的本构方程分别为

注意到方程(26) 是含三次非线性的弯曲波方程,因此需要考虑由梁的大挠度引起的非线性效应,色散效应以及压电耦合效应.当非线性效应和色散效应相互作用并达到平衡时,就会出现孤立波或者冲击波解.

2 椭圆函数展开法

Jacobi 椭圆函数展开法是一种求解非线性方程孤立波解和冲击波解的有效方法[18].下文将运用Jacobi 椭圆函数展开法对该模型下的非线性波动方程进行分析求解.Jacobi 椭圆函数展开形式可以是正弦函数snξ、余弦函数cnξ 和第三类Jacobi 椭圆函数dnξ.首先利用Jacobi 椭圆函数正弦展开法,将w(ξ)展开为snξ 的级数

其中n为解展开的项数,aj为待定系数.为了确定展开项数n的值,需要满足非线性方程最高阶导数项和最高阶非线性项的次数相等,且满足

方程(28)两式平衡可以得到n=1,因此对Jacobi 椭圆正弦函数做一阶展开,就能得到非线性方程的精确解,此时解的形式具体可以表示为

设方程(26)的解为

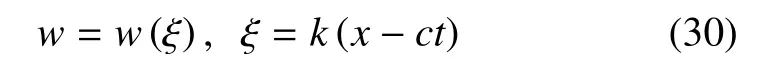
其中k是波数,c是波速.将解的形式(30)代入到非线性方程(26),可以得到非线性常微分波动方程

非线性弯曲波方程解的具体形式可以写为

方程(45) 是非线性弯曲波方程的另一个精确解,显然当δ1<0 且δ3>0 时,上式成立.根据椭圆函数的性质,当模数m趋于1 时,cnξ 趋于sechξ,则方程(45)可以退化为孤立波解形式

特别地,如果运用第三类Jacobi 椭圆函数展开法,当模数m趋于1 时,也可以得到孤立波解.

3 约化摄动法

进一步运用Jacobi 椭圆函数展开法求解非线性薛定谔方程,得到非线性薛定谔方程的振幅为

解(70)和(71)的形式与文献[16]类似,但是方程中系数的含义有很大差别,尤其是在考虑压电效应和电学边界条件以后,孤子解的特性也会受到这些参数的影响,下面将着重讨论.

4 冲击波和孤立波分析

在数值计算中,基体梁采用铝,压电层为PZT 压电陶瓷,压电层合梁的结构参数和压电片的材料参数如下表所示.

表1 压电层合梁参数Table 1 Parameters of the piezoelectric laminated beam

图2 分别给出了线性方程下的色散关系以及对应的相速度曲线和群速度曲线.通过图2(a) 可以看出,随着波数k的增大,频率也随着增大,并且增大的速率越来越快.图2(b) 可以看出,随着波数的增大,群速度大于相速度,也就是说,此时弯曲波有反常的色散.

图2 (a)色散曲线;(b)相速度和群速度与波数的关系Fig.2 (a)Dispersion curves;(b)relationship between phase velocity and group velocity and wave number

首先,考虑压电层厚度和基体梁厚度均为0.05 m,此时可以求得纵波波速c0=2905.4 m/s.图3 分别给出了冲击波解和孤立波解随时间t和空间x的变化,如图3(a)所示.当波速c等于20 m/s 时,结构产生冲击波解,当波速c等于4000 m/s 时,结构产生孤立波解,且冲击波解和孤立波解是非周期的.

图3 不同波速下的冲击波和孤立波Fig.3 Shock wave and solitary wave under different wave velocities

图4 给出了没有加外电压时不同波速下冲击波随空间x的变化曲线.从图4(a) 可以看出,当波速分别为200 m/s 和500 m/s 时,冲击波的振幅分别为0.1 m 和0.25 m.说明随着波速的增大,冲击波的振幅增大.但是当波速c=500 m/s 时,冲击波的波面要比波速c=200 m/s 时的波面要陡,说明冲击波的波宽降低.同样图4(b)给出了不同压电层厚度对冲击波的影响.可以明显看出,当压电层厚度为0.05 m 时,冲击波的振幅大约为0.1 m,当压电层厚度为0.01 m时,冲击波的振幅大约为0.08 m,说明冲击波的振幅和波宽都略有降低.

图5 给出了没有外加电压情况下不同波速下的孤立波解的曲线.由图5(a)可知,当波速c=3000 m/s时,冲击波的振幅约为1.5 m,当波速c=4000 m/s时,冲击波的振幅约为2 m,说明随着波速的增大孤立波振幅增大,同样可以看出孤立波的波宽有所增大.图5(b)给出了压电层厚度对孤立波的影响,可以看出,当压电层厚度为0.05 m 时,孤立波的振幅略大于压电层厚度为0.01 m 时的孤立波振幅,但是当压电层厚度为0.05 m 时的孤立波波宽小于压电层厚度为0.01 m 时的波宽.通过分析图4 和图5 中不同时刻下的冲击波和孤立波的行波曲线,发现冲击波和孤立波都是右行波.

图4 不同(a)波速和(b)压电层厚度下的冲击波Fig.4 Shock wave at different(a)wave velocities and(b)thicknesses of the piezoelectric layer

图5 不同(a)波速和(b)压电层厚度下的孤立波Fig.5 Solitary waves with different(a)wave velocities and(b)thicknesses of the piezoelectric layer

图6 分别显示了波速和压电层厚度对冲击波振幅的影响.由图6(a)可以看出,随着波速的增大,冲击波的振幅增大,当波速较小时,外电压也会对冲击波的振幅产生影响,随着外电压的增大,冲击波的振幅也随之增大.图6(b) 给出了压电层厚度对冲击波振幅的影响,随着压电层厚度的增大,冲击波的振幅增大,且波速较小时,冲击波振幅变化不明显.图7 给出了波速和压电层厚度对冲击波波宽的影响.由图7(a)不难发现,随着波速增大,冲击波波宽有所降低.当波速较小时,随着外电压的增大,冲击波的波宽增大.图7(b) 讨论了压电层厚度对冲击波波宽的影响,随着压电层厚度的增大,且当波速较小时,冲击波的波宽会先减小后增大,对于波速较大的情况,冲击波的波宽变化不明显.总的来说,冲击波的波宽和振幅主要受波速的影响较大,当波速较小时,外电压对冲击波的振幅以及波宽影响较大.

图8 分别给出了不同波速和压电层厚度下的孤立波振幅的变化.由于孤立波产生的条件,所需波速必须大于纵波波速c0,通过图6 和图7 的分析可以确定:外电压的影响在波速较小的情况下对冲击波的振幅和波宽影响较大,当波速较大的时候,压电的影响可以忽略.如图8(a)所示,随着波速c的增大,孤立波的振幅近似为线性增大,且随着电压的增大,孤立波的振幅基本不变.通过图8(b)可以看出,随着压电层厚度的增大,孤立波的振幅逐渐增大,但是增大的幅度逐渐减小,随着波速的增大,孤立波的振幅增大.通过图9(a)和图9(b)可以看出,随着波速和压电层厚度的增大,孤立波的波宽也随之增大,外加电压对孤立波波宽几乎没有影响.

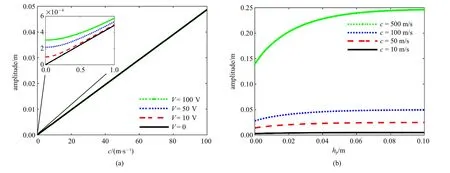
图6 (a)波速和(b)压电层厚度对冲击波振幅的影响Fig.6 Influences of(a)wave velocity c and(b)piezoelectric layer thickness hp on the amplitude of the shock wave

图7 (a)波速和(b)压电层厚度对冲击波波宽的影响Fig.7 Influences of(a)wave velocity c and(b)piezoelectric layer thickness hp on the width of the shock wave

图8 (a)波速和(b)压电层厚度对孤立波振幅的影响Fig.8 Influences of(a)wave velocity c and(b)piezoelectric layer thickness hp on the amplitude of the solitary wave

图9 (a)波速和(b)压电层厚度对孤立波波宽的影响Fig.9 Influences of(a)wave velocity c and(b)piezoelectric layer thickness hp on the width of the solitary wave

5 亮孤子和暗孤子分析

根据亮孤子和暗孤子存在条件,可试图通过调节外电压或者压电层厚度来分别实现亮孤子和暗孤子的条件,所以有必要研究色散系数α 和非线性系数β随压电层厚度hp和外电压V的变化.下面着重分析外加电压和压电层厚度对色散系数的影响.图10(a)给出了外加电压对色散系数的影响,可以看出,随着外加电压V的增大,色散系数呈线性增大.观察到色散系数随着外加电压的增大出现正负变化,当色散系数α >0 时,结构有亮孤子解;当色散系数α <0时,结构有暗孤子解.另外,当压电层厚度hp=0.01 m时,色散系数与外加电压的斜率更大.图10(b)可以看出,随着压电层厚度的增大,色散系数的绝对值先增大后减小,但是色散系数的符号不发生变化.当取不同外加电压时,色散系数的符号才会发生变化,且外加电压对亮孤子解和暗孤子解的影响更大,因此可以通过调整作用在压电层合梁上的电压来实现亮孤子和暗孤子.

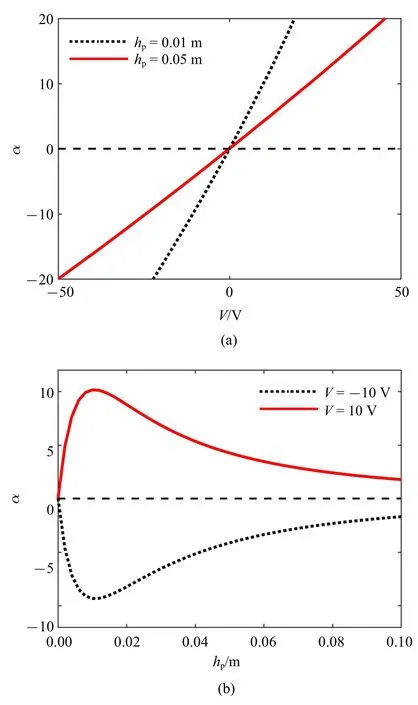
图10 (a)外加电压和(b)压电层厚度对色散系数的影响Fig.10 Influences of(a)external voltage and(b)the thickness of the piezoelectric layer on the dispersion coefficient

接下来给出了不同参数下的亮孤子解和暗孤子解.图11(a)给出了波数k=0.02,外电势V=10 V 和压电层厚度hp=0.05 m 时的压电层合梁中亮孤子解随慢变τ 和ξ 的变化关系,可以看到振幅较大的范围分布主要集中在中心附近的狭小区域内,最大振幅为0.01 m,当离开中心区域,振幅很快下降到零,且随着τ 的变化,亮孤子解的振幅和波形均不发生变化.图11(b)给出了当波数k=0.02,外电势V=−10 V 和压电层厚度hp=0.05 m 时的压电层合梁中暗孤子解随τ 和ξ 的变化关系,可以看到在中心点附近,振幅最小且为零,离开中心点,振幅很快增大并达到最大值,此时最大振幅约为0.01 m.

图11 亮孤子解和暗孤子解Fig.11 Bright soliton and dark soliton

图12(a)给出了不同压电层厚度下亮孤子解的特性,当hp=0.05 m 时,亮孤子解的振幅约为0.021 m;当hp=0.01 m 时,亮孤子解的振幅大约为0.031 m.τ=0 时刻,亮孤子位于中心,τ=5 s 时刻,亮孤子发生右移,且压电层厚度hp为0.05 m 时亮孤子移动的幅度比压电层厚度hp等于0.01 m 时要大,且在移动后亮孤子振幅不发生变化,波形不发生改变.同样通过观察图12(b) 可以发现,当V=10 V 时,亮孤子的振幅约为0.021 m;当V=50 V 时,亮孤子解的振幅大约为0.048 m.在τ=0 时刻,亮孤子位于中心,τ=5 s 时刻,亮孤子发生右移,且外加电压V为50 V时亮孤子移动的幅度比外加电压V等于10 V 时要大,且在移动后亮孤子振幅和波形同样不发生改变.综上,可以得出结论:压电层厚度和外加电压对亮孤子特性有明显的影响.

图12 不同(a)压电层厚度和(b)外加电压的亮孤子解Fig.12 Bright soliton at different(a)thicknesses of the piezoelectric layer(b)external voltages

图13(a) 给出了不同压电层厚度下暗孤子解的特性,当压电层厚度hp=0.05 m 时,暗孤子解的振幅约为0.021 m;当hp=0.01 m 时,暗孤子解的振幅大约为0.031 m.在τ=0 时刻,暗孤子位于中心;τ=5 s时,亮孤子发生左移,且压电层厚度hp为0.05 m 时亮孤子移动的幅度比压电层厚度hp等于0.01 时要大,且在移动后暗孤子振幅不发生变化,波形不发生改变.同样由图13(b)可以看出,当V等于−10 V 时,暗孤子解的振幅约为0.021 m;当V等于−50 V 时,暗孤子解的振幅大约为0.048 m.在τ=0 时刻,暗孤子位于中心;τ=5 s 时刻,亮孤子发生左移,且外加电压V为−50 V 时暗孤子移动的幅度比外加电压V等于−10 V 时要大,且在移动后暗孤子振幅和波形同样不发生改变,因此,压电层厚度和外加电压对暗孤子特性也有明显的影响.

图13 不同(a)压电层厚度和(b)外加电压的暗孤子解Fig.13 Dark soliton at different(a)thicknesses of the piezoelectric layer(b)external voltages

继续研究了压电层厚度和外电压对亮孤子振幅的影响.通过图14(a)和图14(b)可知,随着压电层厚度的增大,亮孤子解的振幅均有所减小,同时减小的幅度随压电层厚度的增大而减小;而随着电压的增大,亮孤子解的振幅增大.

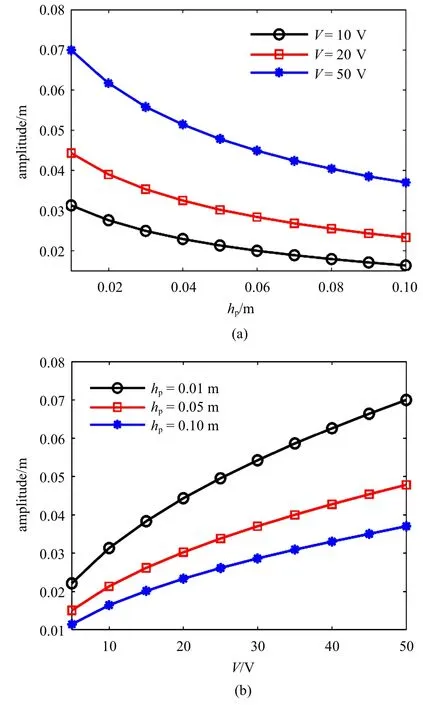
图14 (a)压电层厚度和(b)外加电压对亮孤子振幅的影响Fig.14 Influences of(a)the thickness of the piezoelectric layer and(b)external voltage on the amplitude of the bright soliton

6 总结

本文将矩形压电层合梁简化为一维无限长模型,导出了含有电学边界条件下的矩形压电层合梁的非线性弯曲波动方程.用传统的Jacobi 椭圆函数展开法得到了相应的冲击波解和孤立波解.并用多尺度摄动方法求得了相应的亮孤子解和暗孤子解.得到如下结论:(1)随着波数k增大,频率随之增大,且增大的速率越来越快;随着波数k增大,群速度大于相速度,此时弯曲波有反常色散.(2) 当波速c和小于纵波波速c0时,存在冲击波解,且随着波速c的增大,冲击波的振幅增大,波宽减小;随着压电层厚度hp增大,冲击波振幅增大,波宽先减小后增大;外加电压对波速较小时的冲击波的振幅和波宽有一定影响,随着电压的增大,冲击波的振幅增大,波宽减小.(3)当波速c和大于纵波波速c0时,存在孤立波解,随着波速c的增大,冲击波的振幅和波宽增大;随着压电层厚度hp的增大,冲击波振幅和波宽增大;外加电压对孤立波几乎没有影响.(4)随着外加电压V增大,色散系数α 增大,且外加电压V对色散系数的影响比压电层厚度hp对色散系数的影响更大,可以通过调整作用在压电层合梁上的电压来改变色散系数的符号,得到亮孤子和暗孤子.(5) 随着压电层厚度hp的增大,亮孤子和暗孤子的振幅均有所减小,随着外加电压V增大,亮孤子和暗孤子的振幅增大.