基于流形切空间插值的折叠翼参数化气动弹性建模1)

詹玖榆 周兴华 黄 锐

(南京航空航天大学机械结构力学及控制国家重点实验室,南京 210016)

引言

近年来,世界航空界正着力发展具有飞行环境(如高度、速度、气候等) 自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器.这类飞行器可根据飞行任务需要自主改变结构和气动布局,在复杂的飞行环境条件下保持良好的飞行性能[1-5].在众多变体飞行器设计方案中,折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势,受到了广泛的关注.然而,在机翼受控变体过程中,不仅非定常气动力会随着机翼形状改变而发生变化,机翼的惯性、弹性和阻尼特性也同时发生变化,极易诱发不同结构模态参与的参变颤振现象,给变体飞行器的飞行安全带来挑战.针对不同折叠构型下变体机翼的气动−结构耦合动力学系统的参变特性,如何建立以折叠角为参数的参数化气动弹性模型,在全参数空间内实现气动弹性力学行为的高效、高精度预测,是变体飞行器研制过程中亟待解决的动力学问题.

当前变体飞行器动力学建模研究可分为两大类:一类是多刚体动力学模型(如Newton-Euler 方法[6-8]、Lagrange 方法[9-10]、Kane 方法[11-13]等);另一类是柔性体动力学模型(如浮动坐标法[14]、绝对节点坐标法[15-16]等).相较于多刚体动力学模型,柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析,因此受到更广泛的关注.例如Snyder 等[17]研究了Goland 折叠翼的颤振特性,发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大.Selitrennik 和Karpel[18]对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法.该方法采用虚拟质量法建立系统的结构动力学方程,并通过动力学方程和CFD 技术相耦合的方式,建立了可折叠式变体机翼的气动弹性方程.数值结果表明,瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响.对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题,Lee 等[19]提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法.

上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模,计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为.参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案.Zhao等[20]和倪迎鸽等[21]采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型,分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响.Huang 等[22]提出了一种参数化的气动伺服弹性建模方法,高效地获得了不同折叠角下的机翼气动伺服弹性数学模型,实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析.

然而,上述参数化建模方法均基于子结构综合方法,即根据折叠过程中内外翼结构动力学模型在全局坐标系中的约束关系,采用坐标变换实现全局坐标系下折叠翼结构动力学的快速生成.该参数化建模方法并未从根本上解决不同折叠构型下模态坐标不一致的难题.本文基于流形切空间插值方法,建立以折叠角为参数的折叠翼参变结构动力学模型,并耦合基于偶极子网格法的参数化非定常气动力模型,进而建立折叠翼的参变气动弹性模型.为了验证该参数化模型的准确性,本文选取一小展弦比折叠翼模型为研究对象,通过对结构自由振动分析和颤振边界的预测,考核本文提出的参数化建模方法.

1 折叠翼参数化气动弹性建模

不同于常规机翼的气动弹性分析,折叠翼的气动弹性分析需要在每一个角度重新建立结构动力学模型和气动模型,并将之耦合得到气动弹性模型.为了高效、准确地分析折叠翼的气动弹性力学行为,本节介绍基于流形切空间插值的参数化气动弹性建模方法.模型建立过程分为参数化结构动力学建模、参数化气动力建模和参数化气动弹性建模3 部分.

1.1 折叠翼模型描述及参数化建模目标

折叠翼的几何构型如图1 所示,折叠翼由机身和两个能独立旋转的内外翼组成.折叠翼折叠过程如图2 所示(下标α,β 和γ 分别表示机身结构、内翼结构和外翼结构).内翼可以进行0◦∼120◦的旋转,同时外翼始终保持水平.机身和内外翼的材料均为铝板,其杨氏模量为71 GPa,泊松比为0.33,密度为2.7×103kg/m3,厚度分别为2.0 mm,1.0 mm 和1.0 mm.

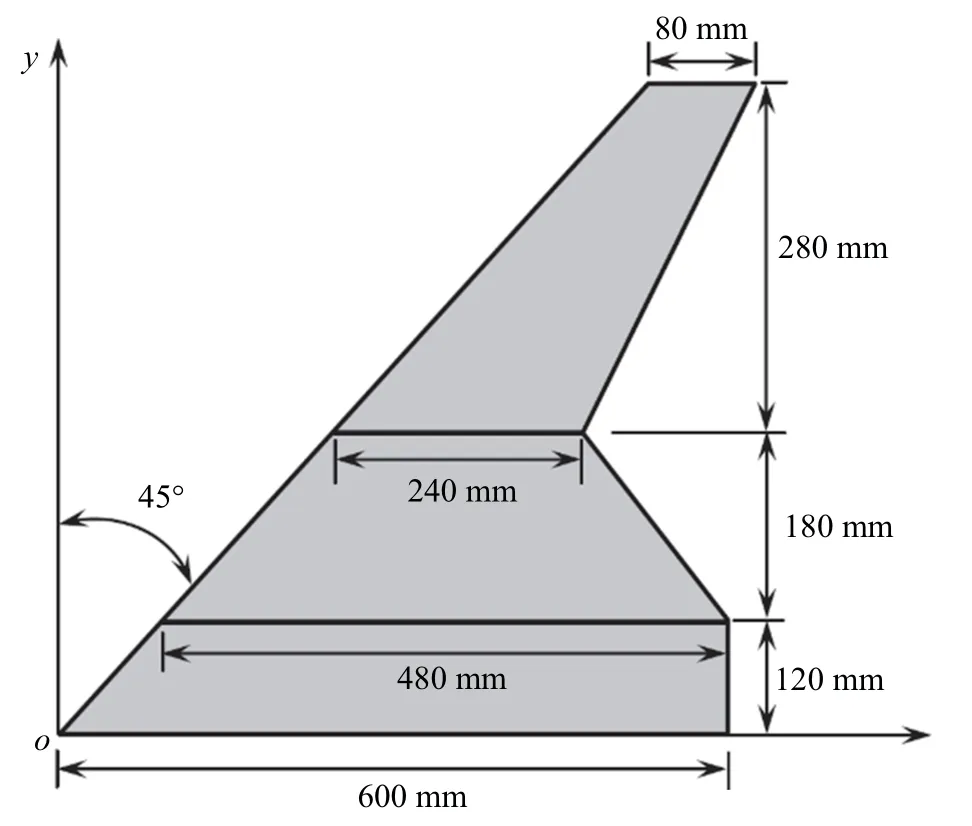
图1 折叠翼几何尺寸及构型Fig.1 Configuration of folding wing

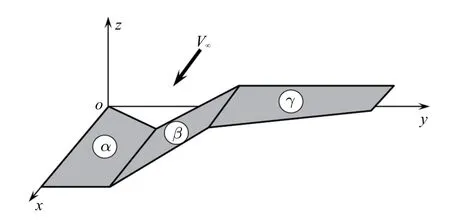
图2 折叠翼折叠过程Fig.2 Morphing process of folding wing

通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵,然后通过子结构综合法[23-24]得到折叠翼结构动力学方程如下

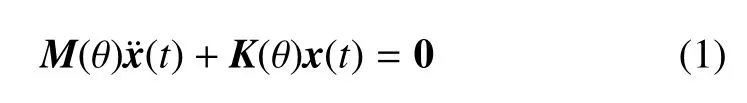
式中,θ 是折叠角,M(θ)是折叠翼的质量矩阵,K(θ)是折叠翼的刚度矩阵,x(t) ∈Rn为物理坐标,值得注意的是,本文没有考虑折叠翼的结构阻尼.因为实际飞行器的阻尼特性难以获得,所以建立参数化的阻尼模型更加困难.由结构动力学方程可以得到折叠翼的振型矩阵Φ(θ)=[φ1(θ) φ2(θ) ··· φn(θ)],取Φ(θ)前m列得到降阶矩阵φ(θ)=[φ1(θ) φ2(θ) ··· φm(θ)],令x(t)=φ(θ)ξ(θ,t),ξ(θ,t)是广义坐标,同时对式(1)左乘φ(θ)T,得到折叠翼的低维结构动力学方程

折叠过程中质量矩阵、刚度矩阵、振型矩阵和气动力矩阵都发生了显著变化,如果要对折叠翼进行气动弹性分析,就需要对每个折叠角进行重复有限元建模和气动力建模,建模效率低下.参数化建模即给出相应参数(如折叠角θ)能快速得到结构动力学模型和气动力模型,这既能提高分析折叠翼气动弹性行为的效率,也为后续折叠翼的颤振主动控制研究打下良好的基础.

1.2 基于流形切空间的结构动力学

矩阵流形是指具有特殊性质(正定性、对称性、正交性或非奇异性)的矩阵组成的流形.在流形上插值得到的矩阵仍具有原矩阵的特殊性质.正因为这一特点,有学者提出基于流形矩阵的插值方法[25-32].令表示由一系列折叠角度所组成的集合,矩阵Pi表示折叠角θi对应的系统矩阵(如质量矩阵、刚度矩阵和振型矩阵),Pi张成的空间Si可视为矩阵流形M 上的一点.参数化建模即对于一个新参数θN,获得其对应的矩阵PN.显然,矩阵流形插值是一个可行的方法,但是通常矩阵流形不是“线性”的,因此需要将矩阵流形上的点映射到“平直”的切空间,在切空间中进行插值,然后再从切空间映射回流形上,其推导过程如下.

图3 给出了流形切空间插值方法的示意图.由于在参数化结构动力学建模中涉及两种不同流形,上述的指数映射和对数映射使用抽象的数学表达形式,下面将具体给出这两种不同流形的插值方法.

图3 流形切空间插值示意图Fig.3 Sketch map of manifold tangent space interpolation

在折叠翼低维结构动力学方程中,Mr(θ)和Kr(θ)均为SPD(symmetric positive definite)矩阵,张成的空间为SPD 流形.SPD 流形的对数映射为

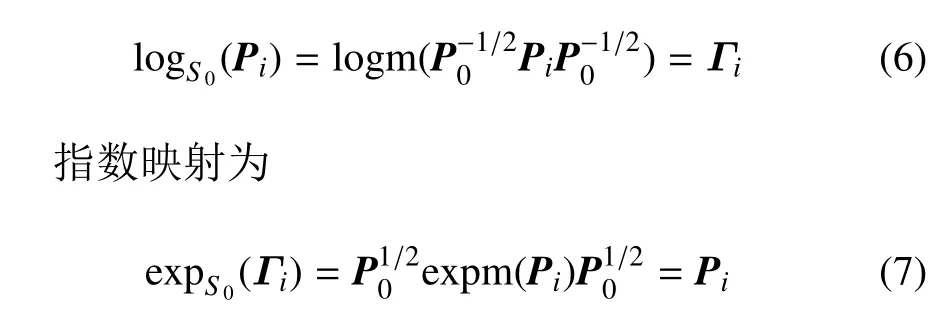
式中,logm 和expm 分别指矩阵对数和矩阵指数.

在气动弹性计算中,还有必要对振型矩阵φ(θ)进行参数化建模.但是φ(θ)是n×m维矩阵,不再适用于SPD 流形切空间插值.同时φ(θ)的列向量表示折叠翼结构的某阶模态,因此参数化振型矩阵的每一列也应该表示折叠翼的某阶模态.为得到参数化振型矩阵,本文引入约束矩阵ϕ(θ),其满足约束条件

1.3 参数化气动力建模

本文基于偶极子网格法(DLM) 建立折叠翼的参数化非定常气动力模型.偶极子网格法通过求解无量纲法洗速度与压差系数的函数来确定空气动力影响系数,从而获得气动网格上的气动力,计算方程如下

Fa是作用在结构网格点上的等效力向量,于是我们得到了由气动力引起的作用在个有限元节点上的参数化的空气动力等效力,如下

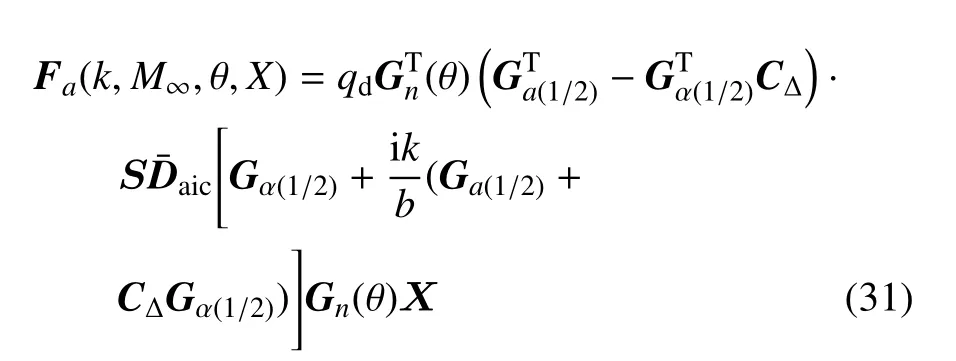
1.4 参数化的折叠翼气动弹性模型

模态空间下,折叠翼参数化气动弹性方程如下

通过参数化的状态空间方程,可求解不同风速、不同折叠角下的气动弹性系统的响应,也可以进行气动弹性稳定性分析.

2 算例验证

本节以小展弦比折叠翼模型为研究对象,分别从结构动力学和气动弹性稳定性两个方面验证本文所提出的参数化建模方法的准确性.结构动力学模拟方面,重点关注参数化模型预测固有频率、固有振型等结构特性随折叠角的变化规律.气动弹性稳定性分析方面,预测折叠翼的颤振临界速度和颤振频率随折叠角变化的规律.

2.1 折叠翼结构动力学特性分析

参数化结构动力学模型的准确性是变体飞行器参数化气动弹性建模的前提.本文首先建立了0◦,10◦,25◦,50◦,80◦,100◦和120◦七个折叠角下的折叠翼有限元模型,通过流形切空间插值得到基于以上角度的参数化结构动力学模型.

如图4 所示,参数化建模方法计算得到的前8 阶模态频率和直接法计算得到的前8 阶模态频率吻合较好.相较于其他折叠角度,基于流形切空间插值的参数化建模方法在预测115◦折叠角下的第8 阶固有频率(预测频率为101.27 Hz)与直接法(计算频率为102.86 Hz)存在一定差异,误差约为1.5%,仍处于工程可接受范围.

图4 参数化建模方法与直接法计算频率对比Fig.4 Comparison of natural frequency between parametric model and direct method

除了结构固有频率之外,折叠翼的结构固有振型对广义气动力的计算以及气动弹性分析的精度也有重要影响.图5 给出了5◦折叠角下参数化建模方法得到的固有振型与直接法得到的振型(蓝色为参数化建模计算的振型,红色为直接法计算的振型)的对比.对比结果表明,参数化建模方法所计算的前8阶固有振型与直接法的计算结果吻合较好.

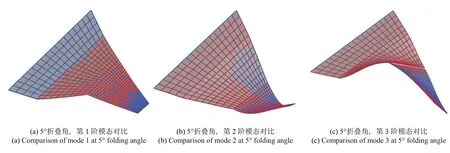
图5 5◦折叠角时,各阶模态对比Fig.5 Comparison of modes at 5◦folding angle

图5 5◦折叠角时,各阶模态对比(续)Fig.5 Comparison of modes at 5◦folding angle(continued)

MAC(modal assurance criterion)值是检验振型函数预测误差的重要指标.为了验证参数化建模方法所预测的固有振型与真实振型的偏差,本文分别给出了在5◦,30◦,65◦和105◦折叠角下折叠翼前8 阶固有振型的MAC 值分布.如图6 所示,除第6 阶弹性模态外,其余各阶模态MAC 值均大于0.99.第6 阶模态出现误差的原因是该插值方法在两个较小的参数值之间可能形成拐点,使得插值结果与真实值产生较大差异.

图6 4 个典型角度下振型的MAC 值Fig.6 MAC values of mode shapes under four specific folding angles

图6 4 个典型角度下振型的MAC 值(续)Fig.6 MAC values of mode shapes under four specific folding angles(continued)

2.2 折叠翼参数化气动弹性建模分析

为了进一步验证该参数化气动弹性模型的准确性,本文采用参数化建模方法计算了折叠翼的颤振边界.如图7 所示,参数化气动弹性模型成功预测了折叠翼颤振边界随折叠角的变化规律:随着折叠角变化,折叠翼的颤振模态发生了复杂的模态切换现象.在0◦∼30◦折叠角区间,折叠翼的第2 阶模态发生颤振.当折叠角位于35◦∼80◦区间时,结构的第3 阶模态发生颤振.在85◦∼105◦折叠角区间,折叠翼发生颤振的是第4 阶模态.当机翼折叠角进一步增大到110◦∼120◦范围时,折叠翼的第3 阶模态再次发生颤振.

此外,本文将参数化气动弹性模型对颤振边界的预测结果与直接法预测的结果进行了对比研究.如图7 所示,在大部分折叠角下,参数化折叠翼模型所预测的颤振临界速度和颤振频率均与直接计算结果吻合较好,频率误差最大值小于1%,颤振临界速度误差最大值低于4%.然而,图示结果表明,在105◦的折叠角处,参数化建模方法所预测的颤振临界速度和颤振频率与直接法计算结果存在较大差异.从颤振频率随折叠角变化的曲线(图7(a)) 来看,发生较大差异的主要原因是参数化建模方法预测的颤振模态分支与直接法计算得到的颤振模态分支不同.为了深入探究引起颤振模态分支变化的原因,图8 分别给出了105◦折叠角下直接法和参数化建模方法计算得到的气动弹性系统根轨迹分布图.如图所示,该折叠角下两种计算方法所预测的根轨迹分布图相似,主要差异在于直接法预测了两种颤振形态.第一类颤振形态是第4 阶模态发生颤振,颤振临界速度是54.6 m/s;第二类颤振形态是第3 阶模态发生小阻尼颤振,颤振临界速度为32.3 m/s.本文提出的参数化建模方法预测的第4 阶模态发生颤振的临界速度是54.2 m/s,与直接法结果吻合较好.

图7 参数化建模方法与直接法气动弹性计算对比Fig.7 Comparison between parametric modeling and direct method in aeroelasticity

图8 参数化模型与直接法计算根轨迹图对比Fig.8 Comparison of root locus calculated by parametric modeling and direct method

和直接法相比,本文提出的基于流形切空间插值的参数化建模方法无须重复进行固有模态分析,计算效率远高于直接法.表1 展示了使用两种方法分别计算图7 所示的颤振边界所需的时间成本对比.直接法是指通过MSC.Nastran 对给定折叠角度下的折叠翼进行有限元模型的设计,并使用商业软件对气动和结构网格进行插值、进行非定常气动力的计算以获得此构型下的颤振速度;而参数化建模的方法不需要手动地重复有限元建模、结构和气动插值,仅仅改变参数即可得到此时结构的刚度、质量矩阵,单次时间为0.7 s,可忽略不计,因此其总时间花费仅为传统方法54.3%.

表1 两种方法计算时间对比Table 1 Comparison of the time cost for the two methods

3 结论

本文提出了一种基于流形切空间插值的折叠翼参数化气动弹性建模方法,实现了折叠翼的气动弹性模型的高效建立.相较于现有的参数化建模方法,本文提出的参变建模方法有效解决了变体过程中存在的模态坐标不一致性.为了验证该参数化模型在预测折叠翼气动弹性力学行为的准确性,本文以折叠翼为研究对象,分别从折叠翼结构固有频率、模态振型、颤振边界等方面进行了算例验证.结果表明,该参数化建模方法可高效、高精度预测可折叠式变体机翼的固有频率和颤振边界随折叠角的演变规律.在后续工作中,可将该方法扩展到解决快速变体过程的时变动力学建模,重点围绕模态坐标一致性问题和时域非定常气动力计算等方面开展研究.