儿童抑郁水平与学业成绩的发展轨迹：基于平行潜变量增长模型 *

2021-05-30姚文玉张思敏丁雪辰徐刚敏

心理与行为研究 2021年2期

姚文玉张雯刘影张思敏丁雪辰,3 徐刚敏

(1 上海师范大学心理学系，上海 200234) (2 华东政法大学文伯书院，上海 200042) (3 上海市中小学在线教育研究基地，上海 200234) (4 华东师范大学心理与认知科学学院，上海 200062)

1 引言

作为一种常见的情绪问题，抑郁是指人们对自我、生活和未来产生消极思维的主观体验，它通过影响个体的思维方式使其始终沉浸于负性情绪之中无法自拔，进而对个体的学习、工作与生活产生负面影响（Hammen, 2018）。已有研究发现，抑郁水平与其他精神疾病风险及自杀等行为均有关（O’Beaglaoich, McCutcheon, Conway,Hanafin, & Morrison, 2020），这给社会带来了一系列沉重的负担（Hoffman, Dukes, & Wittchen,2008）。同样，对于儿童而言，抑郁也是一个持久且频繁出现的公共卫生问题，通常与一系列适应指标相关，如与情绪调节能力呈负相关，与同伴侵害呈正相关，破坏儿童社会功能以及产生严重的家庭问题（郑沁怡, 丁雪辰, 刘影, 万旋傲, 桑标,2019; Wakefield, Bowe, Kellezi, Butcher, & Groeger,2020）。更重要的是，如果儿童的抑郁水平未得到及时有效的干预，则会一直持续至成年期并继续危及工作与生活，甚至导致自杀风险（Ngin et al.,2018; Poznanski, Krahenbuhl, & Zrull, 1976）。鉴于此，关注儿童抑郁水平的发展并探讨其与其他因素间的关联具有重要的意义。

需注意的是，学业成绩可能是影响儿童抑郁发展的一大因素（Andrews & Wilding, 2004）。已有研究发现，学业成绩与抑郁水平呈负相关（丁雪辰, 施霄霞, 刘俊升, 2012; Ding, Fu et al., 2020），但在二者关联的预测方向上仍存一定争议。一方面，较低的学业成绩会导致抑郁水平升高。学业成绩通常与内外化行为指标均存在关联，不良的学业成绩可能会阻碍个体的良好适应（丁雪辰, 邓欣媚, 桑标, 李丹, 2018; Vaillancourt, Brittain,McDougall, & Duku, 2013）。同时，中国社会高度重视儿童的学业成绩，倾向于将教育看作提升个人与家庭社会经济地位、获得成功以及追求更美好生活的重要途径（郑沁怡, 胡娜, 丁雪辰, 2020;Liu, Bullock, & Coplan, 2014），这使得儿童和青少年面临更大的学业压力，并成为抑郁水平的快速发展期（侯金芹, 陈祉妍, 2016）。另一方面，抑郁水平也会影响学业成绩。抑郁情绪会诱发学生对学习的一系列消极态度，包括学习兴趣低、学习拖延以及对学习的情绪紧张感（如考试时头脑空白）等，进而导致学业成绩的下降（Kayani et al.,2018; Kınık & Odacı, 2020）。目前，少数研究通过纵向设计发现了二者间不同的预测方向，包括抑郁水平负向预测个体未来的学业成绩（Verboom,Sijtsema, Verhulst, Penninx, & Ormel, 2014），以及学业成绩负向预测个体未来的抑郁水平（Wallin et al.,2019）。综上，以往研究结论各异导致无法准确把握抑郁水平与学业成绩间的预测关系及其方向。因此，在个体发展过程中进一步探索二者之间的动态关系是有必要的。

以往横向研究的结论无法推断二者之间明确的预测关系，目前的纵向研究也通常仅有两个时间点的数据收集，且传统方法只比较平均值变化并把个体之间的差异作为误差方差，舍弃了误差差异中可能包含的更有价值的信息，无法提供变量完整发展变化的速率（Duncan & Duncan, 2009）。从这一层面来讲，基于更多时间点进行测查并探讨抑郁水平与学业成绩的发展轨迹及相互作用模式，可以进一步揭示变量之间动态发展的关系。潜变量增长模型（latent growth modeling, LGM）是探究变量发展轨迹的一种重要统计方法，一般通过三次及以上时间点的数据来建立模型（Meredith &Tisak, 1990）。相比于仅能体现多变量间静态关系的线性回归模型，潜变量增长模型则能够考察多变量之间的发展轨迹与动态相互作用模式并对个体间的差异有所关注。近年来，已有研究开始尝试通过该方法探讨抑郁水平与其他因素间的关联，发现早期物质滥用可促进早期抑郁水平的发展，并随着时间的推移反过来增加物质滥用的风险，进一步提高未来抑郁水平的风险（Felton,Kofler, Lopez, Saunders, & Kilpatrick, 2015）。

综上，本研究基于三个时间点对儿童的抑郁水平和学业成绩进行测查，同时建立交叉滞后模型与潜变量增长模型，以期从动态视角更好地解释二者的变化趋势及其之间的相互作用模式。基本假设如下：（1）三个时间点上儿童抑郁水平与学业成绩之间呈纵向相互预测关系；（2）儿童抑郁水平和学业成绩发展轨迹的初始水平可以相互预测彼此的发展速率。

2 研究方法

2.1 研究对象

采用简单随机整群抽样法，选取江苏省某小学三年级（331 人）和四年级（204 人）儿童作为研究对象，对10 个班级共535 人（平均年龄9.98±0.83 岁）进行三次测量（各间隔一年），最终纳入分析的被试包括男生286 名，女生249 名。在第二次和第三次施测中分别有约9%和15%的被试因转学、病假、事假等原因流失，MCAR 检验表明被试流失为完全随机缺失，χ2(8)=11.21，p＞0.05。根据Duncan，Duncan 和Li（1998）的建议，采用Mplus 的全信息最大似然法（FIML）处理缺失值。

2.2 研究工具

2.2.1 儿童抑郁量表

采用由Kovacs（1992）编制、俞大维和李旭（2000）修订的儿童抑郁量表以测量儿童的抑郁水平，其中共包含14 个项目，包括悲观、睡眠障碍、疲劳、自我贬低、自杀意向等典型的抑郁症状描述。该工具已被以往研究证实具有良好的信效度，内部一致性为0.88，重测信度为0.81，与应激事件（r=0.43,p＜0.01）和焦虑（r=0.44,p＜0.01）显著相关，适用于考察中国儿童的抑郁水平（吴文峰, 卢永彪, 谭芙蓉, 姚树桥, 2010）。在本研究中，儿童抑郁水平三次测量的内部一致性系数分别为0.80、0.80、0.81。

2.2.2 学业成绩

学业成绩通过教师评价获得，教师对每位学生当前语文、数学和英语的学习成绩进行评分，每个项目均为5 级计分。计算时将每名儿童的语文、数学和英语得分在班级内进行标准化转换，之后合并Z分数值作为用于计算的最终指标。以往研究证实该方法具有良好的信效度，重测信度为0.60，与同伴欺负（r=−0.23,p＜0.01）和孤独感（r=−0.27,p＜0.01）显著相关，适用于考察中国儿童学业成绩的指标（Ding, Chen, Fu, Li, & Liu, 2020;Liu et al., 2014）。

2.3 研究程序

以班级为单位进行集体测试，主试为经过培训的发展与教育心理学专业研究生。施测前，委托教师给每位学生发放介绍本研究的家长知情同意书，获得家长同意并签字后由儿童带回学校，教师统一收回并转交给研究人员。指导语中向被试说明测试目的并作出保密承诺，测试之后立即回收问卷。由于本研究为追踪研究，三次测量之间各间隔一年，三次的测验程序相同，施测总时长均在30 分钟左右。在测验的过程中，所有儿童被试均未表现出对测量项目的理解困难。

3 结果

3.1 描述性统计结果

不同阶段的抑郁水平、学业成绩的相关如表1所示，三次测量中抑郁水平与学业成绩间均呈显著负相关，且在三次测量中表现出较高的稳定性。

表 1 抑郁水平与学业成绩的描述统计及相关分析结果

3.2 抑郁水平与学业成绩的交叉滞后回归分析

采用Mplus 7.4 构建交叉滞后回归模型考察抑郁水平与学业成绩之间的相互预测关系。模型拟合良好，χ2/df=2.07，RMSEA=0.05，CFI=0.99，TLI=0.98。结果如图1 所示：抑郁水平和学业成绩在三次测量中均保持较高稳定性。在控制了自身的稳定性之后，三年中抑郁水平均显著负向预测下一年学业成绩，而学业成绩则只在T1 阶段显著负向预测T2 阶段抑郁水平。

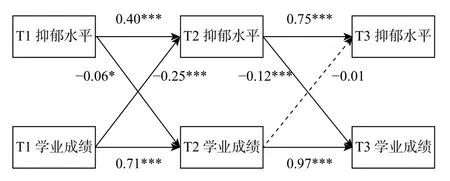
图 1 抑郁水平与学业成绩的交叉滞后模型

3.3 抑郁水平与学业成绩的平行潜变量增长模型

潜变量增长模型可用于考察某一变量的发展轨迹（Meredith & Tisak, 1990），不同于传统方法，该模型可以对发展过程中的个体变异和群组变异同时进行估计（Fan & Konold, 2009）。其中，截距和斜率因子分别代表每个个体的初始水平以及发展速率。在单变量潜变量增长模型的基础上，本研究借助Mplus7.4 构建平行潜变量增长模型（parallel latent growth modeling），通过设置增长因子间的回归方程以更好地揭示抑郁水平与学业成绩的发展轨迹及两者之间的动态相互作用（王孟成, 毕向阳, 2018）。

为检验抑郁水平的发展轨迹，首先构建抑郁水平的潜变量增长模型。抑郁水平的无条件模型拟合结果：χ2/df=0.84。模型的截距即抑郁水平的初始水平为1.33，显著高于0（p＜0.01）。抑郁水平在三次测量期间较为稳定（β=−0.01,p=0.21）。截距的变异（σ2=0.06,p＜0.001）和斜率的变异（σ2=0.02,p＜0.001）均显著高于0，即抑郁水平的初始水平及变化速率存在显著的个体差异。截距与斜率之间（σ2=−0.02,p＜0.001）存在显著负相关，即个体初始抑郁水平越高，其抑郁水平增长的速度越慢（见图2）。

图 2 儿童抑郁水平的发展轨迹

图 3 儿童学业成绩的发展轨迹

其次检验学业成绩的变化轨迹，学业成绩的无条件模型拟合结果：χ2/df=0.02。模型的截距即学业成绩的初始水平为0.00，未显著高于0（p=0.93）。学业成绩在三次测量期间较为稳定（β=−0.01,p=0.58）。截距的变异（σ2=0.67,p＜0.001）显著高于0，而斜率的变异（σ2=−0.05,p=0.15）没有显著高于0，即学业成绩的初始水平存在显著的个体差异，但变化速率的个体间差异不显著。截距与斜率之间（σ2=0.04,p=0.41）无显著相关（见图3）。采用平行潜变量增长模型将抑郁水平和学业成绩作为两个平行的发展过程，通过设置增长因子间的回归方程考察二者间的影响过程，并将性别作为协变量控制。如图4 所示，该模型的拟合良好，χ2/df=1.76，RMSEA=0.04，CFI=0.99，TLI=0.98。初始水平下，抑郁水平与学业成绩呈负相关（r=−0.08,p＜0.01），即个体初始抑郁水平越高，其学业成绩越差。初始抑郁水平负向预测抑郁水平的变化速率（β=−0.55,p＜0.001），即初始抑郁水平高的个体，抑郁水平的增长速率越慢，呈现出补偿效应。学业成绩的初始水平负向预测抑郁水平的发展速率（β=−0.21,p＜0.01），即初始学业成绩越高的个体，其抑郁水平的发展速度越慢，起到保护作用。抑郁水平及学业成绩的初始水平对学业成绩的发展速率均无显著影响。

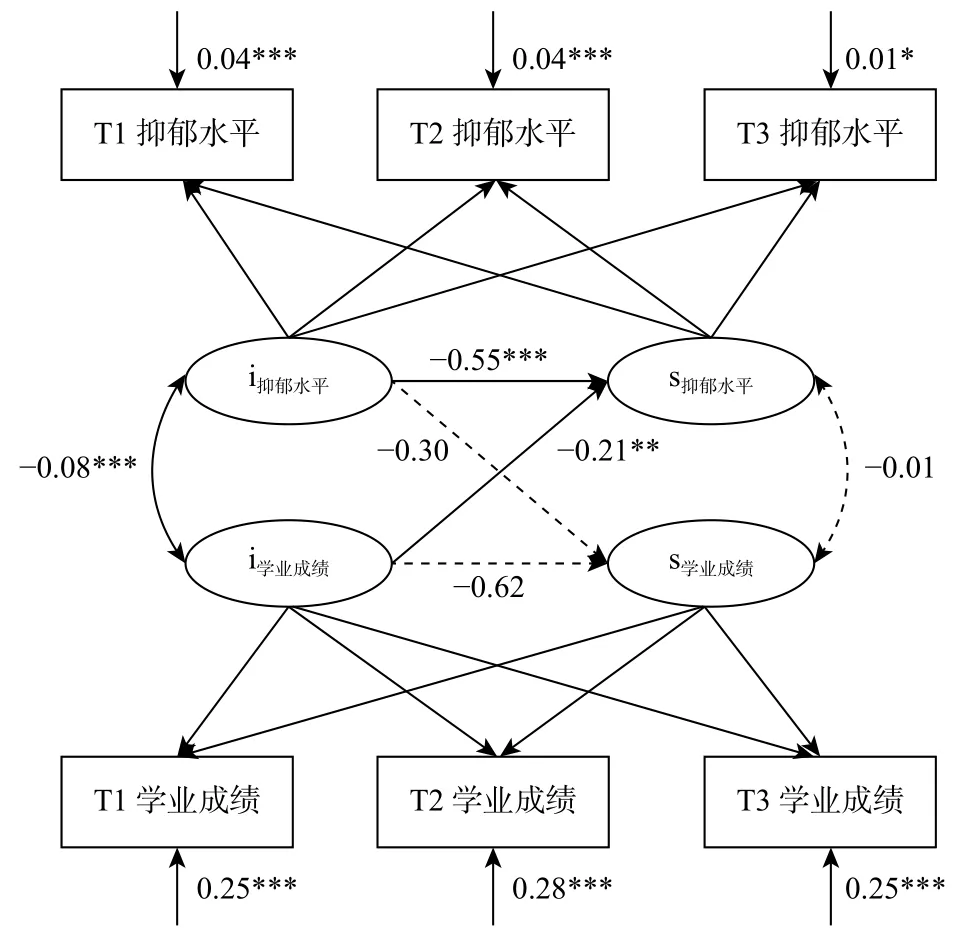
图 4 抑郁水平与学业成绩的平行潜变量增长模型

4 讨论

4.1 儿童抑郁水平和学业成绩的相互预测关系

本研究通过构建交叉滞后回归模型发现，三年测量中抑郁水平均可以负向预测后一年学业成绩，但仅第一年的学业成绩能够显著负向预测第二年的抑郁水平。一方面，儿童抑郁水平越高，其未来的学业成绩越低，这与已有研究结果相一致（Verboom et al., 2014）。抑郁情绪会使个体出现兴趣减退、动力不足等情况（American Psychiatric Association, 2013），高抑郁水平儿童可能出现逃课或上课注意力不集中等行为，从而致使学业成绩下降。另一方面，与已有研究结果一致（丁雪辰等, 2012），儿童第一年的学业成绩越低，第二年的抑郁水平则越高，这可能由学业压力导致，中国文化下学业压力通常由学校考试、课业及家庭作业所引起，并进一步影响抑郁情绪（Wallin et al., 2019）。此外，这也可能受自我认知的影响，学业成绩对学业自我知觉的影响在低年级时更为明显（Fu, Lee, Chen, & Wang, 2020），加之儿童从社会环境中得到的负面反馈，加剧了其已感受到的抑郁症状。然而，第二年学业成绩不能显著预测下一年抑郁水平，这可能是由于随着年龄增加，儿童开始逐渐关注于不同领域的自我知觉且更易受此影响，如体育锻炼、人际交往等（张雯,周同, 丁雪辰, 周楠, 2020; Harter, 2012）。当然，这也可能受先前路径的影响，在学业成绩影响个体抑郁水平升高后，抑郁情绪会表现于兴趣消退或动力不足之上，使得学业成绩的直接影响不再显著。

4.2 儿童抑郁水平和学业成绩的发展轨迹及其动态关系

本研究的主要目的在于通过构建平行潜变量增长模型考察儿童抑郁水平与学业成绩的发展轨迹及其之间的动态相互作用。研究结果发现，儿童的抑郁水平保持较为稳定的状态，即小学儿童抑郁水平的形成将会影响其后续水平的高低，这为预防抑郁水平升高的必要性提供了一定的理论基础。

在初始水平下，儿童的抑郁水平与学业成绩之间呈负相关，即初始抑郁水平越高的个体，其学业成绩越差，这与前人研究结果基本保持一致（Liu et al., 2018; Wallin et al., 2019）。这种负相关可能通过同伴侵害的路径实现（Liu et al., 2018）。儿童受到身体伤害或关系伤害后会引发内外化问题，进而降低个体对学业的投入程度，最终造成学业成绩的下降（Hoglund, 2007）。同时，高抑郁水平个体会出现兴趣减退及认知功能损害等问题，这可能使其无法积极参与到课堂之中，易出现经常缺课或注意力分散等不良情况，导致学业成绩的下降（Kayani et al., 2018; Verboom et al.,2014）。另一方面，抑郁水平的胜任力模型（the competency-based model of depression）（Cole, 1991）认为，在一个或多个功能领域表现不佳的儿童会收到他人的消极反馈，从而引发儿童的消极自我认知，影响其抑郁水平。学业成绩优异的儿童通常得到他人的一致赞赏与尊重，而成绩较差的个体可能会得到来自父母、同学、老师和其他人的消极评价（Phillipson & Phillipson, 2007），易引发其消极的自我认知，进而引发抑郁问题（Fu et al.,2020; McLeod, Uemura, & Rohrman, 2012）。最后，在中国集体主义文化下，学业成绩更受重视且对获取有限高等教育资源较重要，因此自幼儿时代起，父母便对儿童的学业成绩提出多种要求与期望（丁雪辰等, 2012; 郑沁怡等, 2020），而父母期望又与抑郁水平相关联（王明忠, 范翠英, 薛娜, 周宗奎, 2015），这使得儿童抑郁水平与学业成绩之间建立起关联。

本研究发现初始抑郁水平较高的儿童在后续抑郁水平的发展速度上更慢，更重要的是，初始学业成绩较高的儿童在未来抑郁水平的发展速度上更慢，这为学业成绩作为抑郁水平的保护因素提供了重要证据。资源增长模型（resource-potentiating model）（Kupersmidt, Griesler, DeRosier, Patterson, &Davis, 1995）认为，理想条件会增强个人能力或社会资源，有助于个体的适应性发展，而不利条件则会抑制适应性发展，这可用于解释学业成绩对抑郁水平的保护作用。学业成绩的高低作为影响个体适应性发展的重要资源，随着时间的推移，学业成绩较好的儿童在社会、学校和心理上的适应能力可能会逐渐增强，使得抑郁水平的发展速度变慢。此外，由于中国文化中人们对学业成绩的普遍重视，学业成绩能够在一定程度上帮助存在内化问题的儿童避免受到同伴侵害等适应问题（丁雪辰等, 2018; 丁雪辰等, 2012），从而助使抑郁水平的发展速度放缓。基于此，在重视学业成绩的中国文化背景下，该结果对设计预防儿童抑郁水平升高的干预措施具有启示意义。具体而言，若学校和家长能及时发现儿童在学业成绩上的不足，就更有可能提前感知到儿童抑郁水平的升高，进而通过对儿童进行及时、合理、有效的学业辅导来降低儿童的抑郁水平。不同于以往的认知干预，促进学业投入和动机的干预模型可以更直观便捷地为儿童抑郁水平的降低提供独特的成效（Hudley, Graham, & Taylor, 2007）。

4.3 研究局限与展望

本研究通过为期三年的追踪研究考察了中国儿童抑郁水平的发展轨迹及学业成绩在其中的重要作用，其研究意义包括：第一，中国文化下学业成绩更受重视，儿童容易承担更大的学业压力继而诱发一系列潜在的心理健康问题，这是值得关注的一个社会性发展问题。第二，由于以往采用横断设计以及基于两个时间点的追踪研究均无法准确把握抑郁水平与学业成绩间关系的预测方向以及可能的动态变化（Ding, Fu et al., 2020;Verboom et al., 2014），本研究采用平行潜变量增长模型从动态视角更好地揭示了二者发展轨迹及其之间的相互作用模式，提供了实证依据。第三，本研究具有一定实践意义。学业成绩被发现是抑郁水平的一大保护因素，这给予教育工作者及养育者一定启示，即在日常的学习生活中，对较高抑郁水平的学生应从学业成绩上给予更多鼓励与支持（Chirkov & Ryan, 2001），对于学业成绩较低的后进生也应给予足够关怀以预防其抑郁水平的发展。

本研究也存在一些不足之处。例如，在个体进入青春期后，抑郁水平出现明显上升趋势（侯金芹, 陈祉妍, 2016），而由于学习环境的变化、自我意识的发展、心理生理的变化（Paul & White,1990），抑郁水平与学业成绩间的动态作用模式可能会发生变化。未来研究可将研究对象扩展至初高中以探究二者间关系的发展。此外，本研究虽基于三个时间点的测量建立了平行潜变量增长模型，但三次测量仍无法提供更为详实的证据。未来可通过延长追踪时间来建立非线性潜变量增长模型以更全面地探讨二者间的长期动态关系。