滚针凸度修型对滚动轴承应力分析的影响
2021-05-29姚芳,程林
姚 芳,程 林
滚针凸度修型对滚动轴承应力分析的影响
姚 芳,程 林
(滁州职业技术学院,安徽 滁州 239000)
针对滚针凸度修型及修型半径对滚动轴承应力分布的影响,课题组以KIRD234021型滚动轴承为研究对象,分别建立滚子无凸度和相切圆弧修型两种模型,当修型R弧半径在300~1000mm范围内时,分别计算其轴承内圈滚道应力。研究结果表明:当滚子为无凸度修型时,内圈滚道最大接触应力为6404MPa,此区域亦为形变及磨损最严重处,其数值超过材料热处理后的许用接触应力4000MPa,极易导致轴承滚子及滚道产生点蚀及剥落进而失效;当滚子为相切圆弧修型、直母线L为5mm及R弧为300~800mm时,滚道最大接触应力普遍较低,此时对应滚针凸度范围为0.002~0.006mm。
滚动轴承;凸度修型;R弧半径
自20世纪60年代以来,“边缘效应”引起轴承过早疲劳失效的问题受到了各国学者的广泛关注,并成为摩擦学研究的一个重要课题——凸度设计[1]。轴承滚子凸度设计包含两大部分:合理的凸度量和有效的凸型。设计出合理的凸型是研究轴承滚子的灵魂所在。滚子凸型一般有5种样式,即:直线型、圆弧半凸型、圆弧全凸型、修正线型和对数型[2]。Lundberg[3]最早给出了理论对数凸度方程,可使得滚子应力分布较为均匀,但存在滚子端部不连续的缺点。Johns等[4]改进了Lundberg曲线端部不连续的缺点,提出了近似理论对数凸度方程,但改进后滚子很难获得均匀的应力分布。Horng等[5]提出了圆弧凸型滚子的设计公式,对不同工况下圆弧凸型的参数选取进行了分析。马家驹等[6]通过对Johns-Gohar凸度方程增加一个系数提出了工程对数凸度方程,这种凸度设计方法可以在一定程度上避免边缘应力。Hiroki等[7]提出了优化对数凸度方程,引入了3个系数,由于这3个系数难以精确控制,因此该对数凸度方程没有得到推广应用。
以上研究人员主要从理论出发,缺乏与实践相结合。本文主要针对工程实践,以某企业现有的具体轴承型号为例,主要研究2种滚子凸型(直线型和相切圆弧修型母线),对同种模型的不同凸度值进行受力分析。最终给出在工程实际加工中,同种类型的圆柱滚子轴承,当滚子为相切圆弧修型母线时最合理的凸度范围,可为圆柱滚子轴承的设计和实际生产提供参考。
1 有限元模型
图1分别为滚子直线型和相切圆弧修型模型。两模型均利用CATIA软件建立三维数模,导入Nastran中的Sweep模块进行网格前处理,对其模型进行六面体网格划分,分别获得有限元模型节点数量286351、302542,单元数量86542、89627。
图1 不同修型方式有限元模型
2 滚子凸度修型方式
本文以圆柱滚子轴承KIRD234021的滚子与内圈之间的接触为例,分析滚子不同修型方式的应力分布情况,轴承主要几何参数见表1[8]。

表1 KIRD234021轴承主要参数
图2为轴承滚子两种修型方式。图2(a)为最为常见平头滚子(滚子无凸度)。传统的滚子轴承在设计时,其母线大多采用直母线型,期望轴承滚子承受的载荷能沿着滚子母线方向均匀分布。但在实际使用时发现滚子端面存在较为严重的边缘效应,因此,在实际加工过程中常常对直母线滚子进行修型处理。
在实际运行过程中,滚子在载荷作用下,极易产生偏载现象。因此,人们就提出了相切圆弧修型母线,如图2(b)。轴承滚子母线由中间直线和两端圆弧曲线构成。因此,边缘效应较轻,且有效接触长度较长,高达滚子本身长度的70%左右。
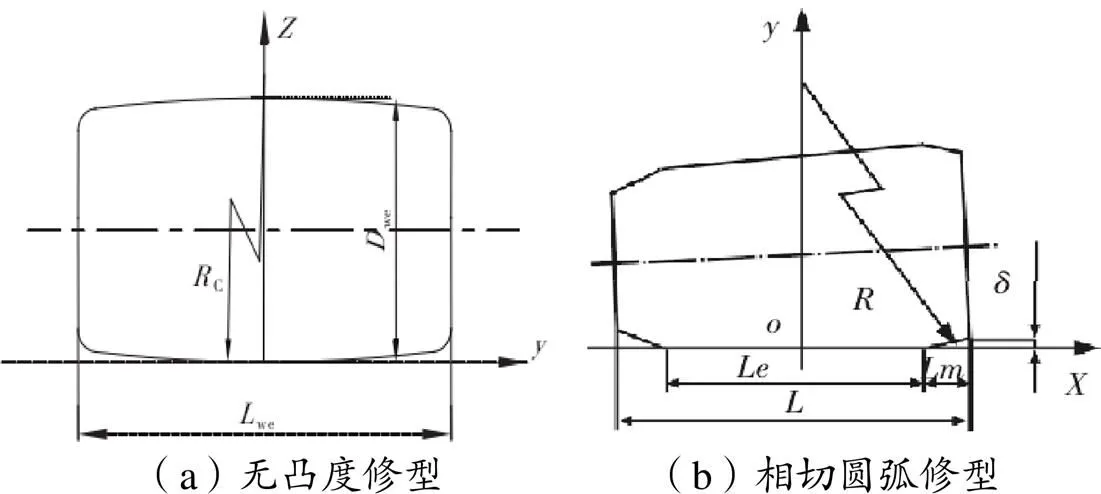
图2 轴承滚子修型方式
3 有限元仿真分析
3.1 滚子无凸度修型时内圈滚道接触应力
图3为滚子无凸度修型时内圈滚道接触应力云图。内圈尽可能按照图纸尺寸建模,其固定端采用刚性轴承固定,该结构为悬臂梁结构[9]。

图3 滚子无凸度内圈滚道接触应力云图
由图3可知,内圈滚道下沿右侧(图3圆圈区域)最大接触应力为6404MPa,此处为接触应力最大区域,亦为形变及磨损最严重处,其数值超过了材料热处理后的许用接触应力4000MPa,致使轴承内圈滚道及滚子端部,极易产生疲劳、点蚀及剥落,进而失效。
3.2 滚子相切圆弧修型(直母线5mm)
图4是直母线为5mm时,不同R弧修型时内圈滚道接触应力云图。
图4(a)为R弧300mm时内圈滚道应力云图。由图可知,轴承滚道两侧的边缘有明显的应力集中。
图4(b)为R弧400mm时内圈滚道应力云图。由图可知,滚道最大接触应力为1391MPa,较图4(a)略有下降,且应力集中带呈现上移的趋势,存在少量偏载现象。

从图4(a)到图4(e)可知,内圈滚道最大接触应力值不断降低,由最高的1406MPa下降至1357MPa,应力集中带不断上移,且存在少量的偏载现象。
从图4(e)到图4(h)可知,内圈滚道最大接触应力值不断上升,由1357MPa激增至2886MPa,虽然应力值上升了,但应力集中现象有所缓解,几乎不存在偏载现象。
3.3 滚子两端修行中间4mm直母线
图5是直母线为4mm时,不同R弧修型时内圈滚道接触应力云图。
图5(a)为R弧300mm时内圈滚道应力云图。由图5(a)可知,此时滚道最大接触应力值为1477MPa,且滚道两侧的中间区域存在较为明显的应力集中现象。
图5(b)为R弧400mm时内圈滚道应力云图。由图5(b)可知,滚道最大接触应力为1468MPa,较图5(a)略有下降,且应力集中带呈现向两侧扩展的趋势,存在局部偏载的现象。
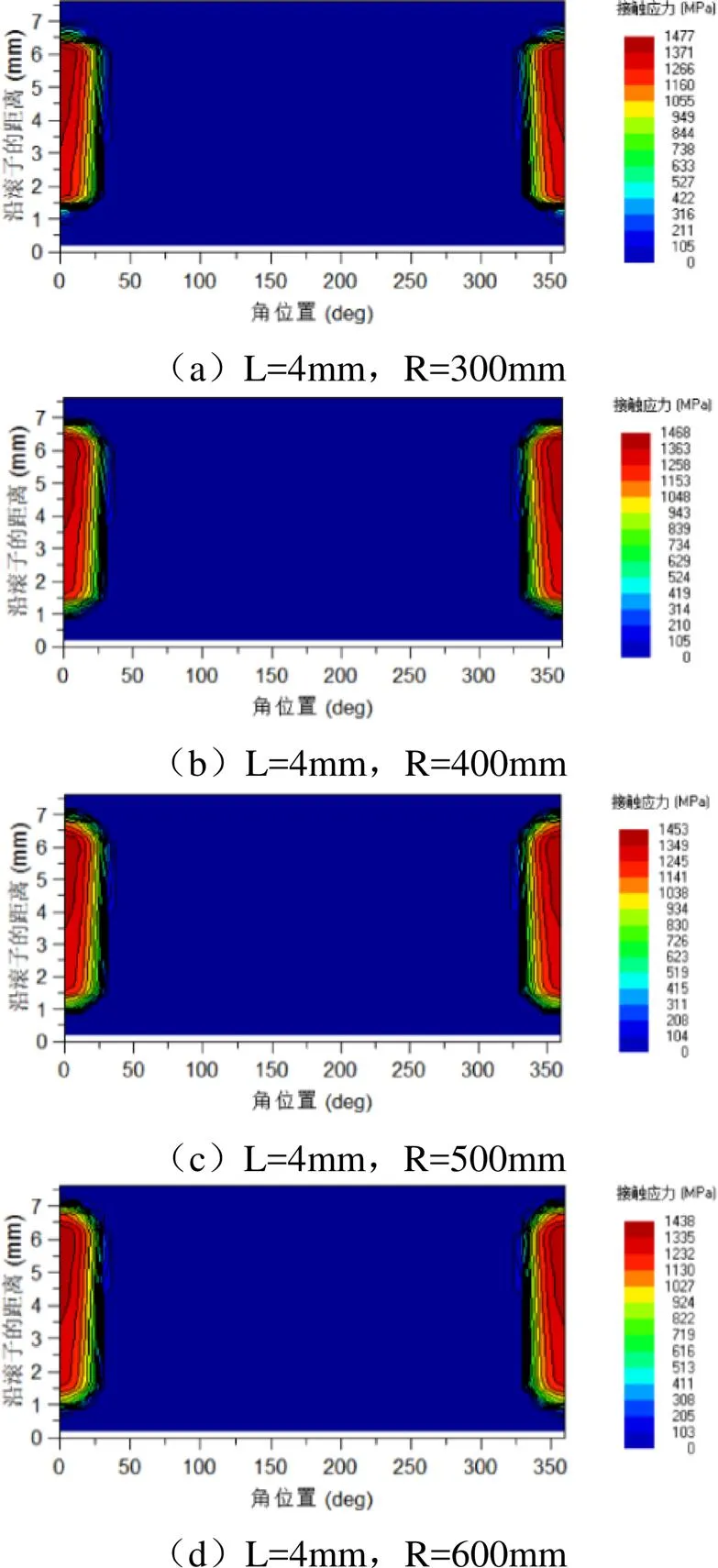
从图5(a)到图5(h)可知,内圈滚道最大接触应力值不断下降,由最初的1477MPa下降至1398MPa,且应力集中带呈现向两侧扩展的趋势,存在少量的偏载现象。
表2为相切圆弧修型时,不同修型R弧时内圈滚道最大应力值。

表2 内圈滚道最大接触应力计算值
由表2可知,当直母线L为4mm时,滚道最大接触应力值随R弧的增大而降低,但根据工程实际情况,R弧不能过大,否则影响加工工艺及生产效率。
当滚子直母线L为5mm及R弧半径为300~800mm时,内圈滚道最大接触应力普遍较低。而R弧半径为900~1000mm时,最大接触应力激增,因此,实际生产加工中应避开此范围。
4 结论
本文结合工程实际,以某企业现有的具体轴承型号为例,主要研究2种滚子凸型(直线型和相切圆弧修型母线),对同种模型的不同凸度值进行受力分析。发现:(1)对滚子进行凸度修型,能够有效提高应力分布均匀性,缓解应力集中现象;(2)当滚子直母线L为5mm及R弧半径为300~800mm时,滚道最大接触应力值普遍较低,此时滚子对应凸度范围为0.002~0.006mm。研究结果可为生产提供参考。
[1] 刘良勇, 孙朝阳, 张延彬. 滚子不同修形母线接触应力分布对比[J]. 哈尔滨轴承, 2015 (1): 6–8.
[2] 王世峰, 段富宣, 姚志国. 制造技术与机床[J]. 制造技术与机床, 2018(7): 91–92.
[3] LUNDBERG G. Elastic contact between two semi-infinite bodies[J]. Forschung auf den gebiete des ingenieurwesen, 2016(5): 201–211.
[4] JOHNS P M, GOHAR R. Roller bearings under radial and eccentricloads[J]. Tribology international, 2017, 14: 131–136.
[5] HORNG T L, JU S H, CHA K C. A deformation formula for circularcrowned roller compressed between two flat plate[J]. ASME journal of tribology, 2017, 122: 405–411.
[6] 马家驹, 徐文, 刘双表. 对数滚子的工程设计[J]. 轴承,2018(6): 2–5.
[7] HIROKI F, TATSUO K, TAKUJI K. Optimized logarithmic roller crowning design of cylindrical roller bearings and its experimental demon-stration[C]// Proceedings of the ASME/ STLE 2017 international joint tribology conference, memphis, TN, USA: American society of mechanical engineers, 2017: 217–219.
[8] 王超. 高铁圆锥滚子轴承滚子与滚道间的接触分析[J]. 北京交通大学学报, 2017(4): 91–97.
[9] 温丽超. 航空发动机中介轴承滚子端磨故障分析及轴承改进设计[D]. 哈尔滨: 哈尔滨工业大学, 2019.
Influence of Needle Roller Profile Modification on Stress Analysis of Rolling Bearing
YAO Fang, CHENG Lin
(Chuzhou Vocational and technical colleges,Chuzhou, Anhui239000, China)
For the influence of needle roller profile modification and modification radius on stress distribution of rolling bearing, the KIRD234021 rolling bearing is taken as the research object to establish two modification models of roller: zero-convexity and tangent arc, and calculates the bearing inner ring raceway stress respectively when the radius of modification R arc is in the range of 300~1000mm. The research results show that: when the rollers are zero-convexity, the inner ring raceway deformed and worn out mostly with a maximum contact stress of 6404MPa, exceeding the allowable contact stress of 4000MPa after heat treatment, which would easily lead to a breakdown due to the bearing roller and raceway pitting and spalling; in tangential arc model, when the straight busbar L is 5mm and R arc in the range of 300~800mm, the maximum contact stress of raceway is generally low, and the corresponding crowning range of needle rollers is 0.002~0.006 mm.
rolling bearing; profile modification; R-arc radius
TH133.33
A
2095-9249(2021)06-0031-04
2021-06-21
安徽省自然科学基金项目(KJ2021A1411);滁州职业技术学院自然科学项目(YJY-2020-23)
姚芳(1987—),女,安徽桐城人,讲师,硕士,研究方向:测量学、仿真学。
〔责任编校:吴侃民〕
