学好高中数学的一点思考

甘肃 陕西

笔者从事高中数学教学已经三十多年，并且教出了一些高材生，但是对于如何让高中生轻松愉快地学好数学，还是感到一筹莫展.众所周知，初中数学只要练熟，就能得高分，但是高中数学只靠“刷题”还是远远不够的，全国名师葛军老师也不赞成无谓的“刷题”.根据教学经验，笔者总结了学好高中数学的三字诀:背，悟，练.

一、“背”

一是要在理解的基础上，灵活记忆，可起到巧“背”的目的.要背定义、定理、公理、公式和一些常用的二级结论，只有将这些基础知识烂熟于心，才能在解题的时候想起要用的内容，反过来做题的过程也是对这些基础知识加深理解的过程.如2016年全国卷Ⅱ理科第12题的条件f(-x)=2-f(x)，如果不熟悉下面的二级结论“对于函数f(x)，如果满足f(a+x)+f(a-x)=2b(即f(2a-x)+f(x)=2b)，则函数f(x)的图象关于点(a,b)对称”，那么就不知道该题的题意是已知函数f(x)的图象关于点(0,1)对称，也就不会灵活运用函数图象的对称性去完美的解决问题，只能靠“蒙”.

二是要“背”每个知识点的命题方向有哪些，并梳理出解决各类题型的常用方法.这样做虽然看起来有点死板，但是有助于培养学生归纳总结的能力，不然遇到每个题目都是新问题，需要重新思考，这样就浪费了时间.由于高考数学考试仅有120分钟时间，所以要考出好成绩，绝对不能浪费每一分钟.例如:在解三角形问题中，如果已知三角形的一边及其对角，那么目标问题的设置常有两类:一类是求三角形的面积的最大值(详见例1)；另一类是求解与边有关的问题(详见例2).

【例1】(2013·全国卷Ⅱ理·17)△ABC的内角A,B,C的对边分别为a，b，c，已知a=bcosC+csinB.

(Ⅰ)求B；

(Ⅱ)若b=2,求△ABC面积的最大值.

解析:(Ⅰ)因为a=bcosC+csinB，所以由正弦定理得sinA=sinBcosC+sinCsinB，则sin(B+C)=sinBcosC+sinCsinB，

即sinBcosC+cosBsinC=sinBcosC+sinCsinB，化简得cosBsinC=sinCsinB.

【例2】(2020·全国卷Ⅱ理·17)△ABC中，sin2A-sin2B-sin2C=sinBsinC.

(Ⅰ)求A；

(Ⅱ)若BC=3，求△ABC周长的最大值.

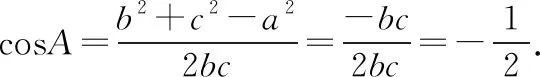
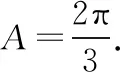
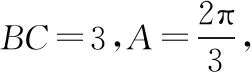
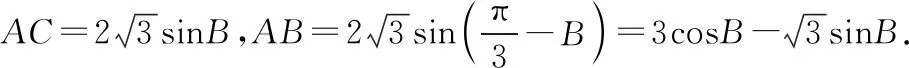
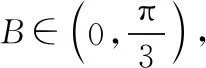
一般地，与边长有关的问题，还有如求2b-c,b2+c2等取值范围的问题，采用正弦定理转化为三角函数问题讨论比较方便.

三是要“背”一些题型的常用解题方法和技巧.要考出好成绩，既要做“学霸”，又要做“考霸”.全国名师四川代尔宁老师说:他和一些高考命题人交谈过，一些高考题，尤其是选择题和填空题基本上都会有其独特的解题方法.基于此，教师在解题教学过程中，既要教给学生常用的通性通法，又要有意识地去引导学生掌握一些解题的高招妙法，这样不但让学生牢固掌握了基础知识，又启迪开发了学生的智慧，同时可以提高学生处理非解答题的速度与准确性.诚如此，我们何乐而不为呢？

()

A.30° B.45°

C.60° D.120°

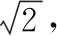
二、“悟”

初中数学一般情况下都是已知条件和要求的结论非常明确，只要功底扎实，解答问题一般不会出错；但是高中数学的已知条件和要求的结论有的非常隐蔽，需要自己“悟”.

【例4】已知定义在R上的奇函数f(x)，当x>0时，函数为f(x)=lnx，则函数y=f(x)的零点个数是

()

A.1 B.2

C.3 D.4

剖析:这道题是一道非常简单的题目，但出错率不低，就是没有“悟”出隐含条件:若函数f(x)为奇函数，且在x=0处有定义，则f(0)=0.许多学生只考虑奇函数的图象关于原点对称，而得到2个零点，故选B，这是个错误答案.实际上，本题应该选C.

【例5】已知定义在R上的函数y=f(x)为增函数，且函数y=f(x+1)的图象关于点(-1,0)成中心对称，若实数a,b满足不等式f(4a-a2)+f(b2-2b-3)≤0，则当2≤a≤4时，a2+(b-1)2的最大值为________.

解析:定义在R上的函数y=f(x)为增函数，且因为函数y=f(x+1)的图象关于点(-1,0)成中心对称，所以函数y=f(x)的图象关于坐标原点对称，所以y=f(x)为奇函数.于是，根据不等式f(4a-a2)+f(b2-2b-3)≤0，先由y=f(x)为奇函数得f(b2-2b-3)≤f(a2-4a)，再由y=f(x)为增函数得b2-2b-3≤a2-4a，所以a2+(b-1)2≤2a2-4a+4.

从而，当2≤a≤4时，根据2a2-4a+4≤2×42-4×4+4=20，可得a2+(b-1)2≤20.故所求a2+(b-1)2的最大值为20.

()

A.{1} B.(-∞,-2]∪[4,+∞)

C.[-4,2] D.[-2,4]

因为函数y=f(x-1)的图象关于点(1,0)中心对称，所以函数f(x)图象关于点(0,0)中心对称，即函数f(x)为R上的奇函数.

又因为实数s,t满足不等式f(s2-2s)≤-f(2t-t2)在1≤s≤4时成立，所以f(s2-2s)≤f(t2-2t)，即s2-2s≥t2-2t.又因为当1≤s≤4时，s2-2s∈[-1,8]，所以t2-2t≤-1，即(t-1)2≤0，所以t=1,故选A.

上面两道题表面上是函数y=f(x+1)的图象关于点(-1,0)成中心对称，函数y=f(x-1)的图象关于点(1,0)成中心对称，但是通过反思得出它们实际上是一回事，均表示函数f(x)的图象关于原点对称，即函数f(x)为奇函数.进一步提炼可给出其隐藏的具有一般性的内在规律:函数f(x+a)的图象关于点(-a,0)成中心对称⟺函数f(x)为奇函数.这就是我们“悟”出的道理，可见反思的重要性！

三、“练”

要学好数学，做练习题，必须有一定的量，但也不是练得越多越好.实际上，我们做一道题的真正目的是不再做这类题，做会了没有必要反复再做.要练，必须努力做到以下几点.

一是要规范.数学学科自身特点要求严谨、规范、准确，而许多学生平时练题，为了赶时间而随便做题，久而久之养成了不严谨、不规范的习惯，导致在考试中处理解答题时失分较多.因此，我们平时练习时一定要规范完成，养成良好习惯，打好扎实的数学基本功.

二是要归类.古人云:学而不思则罔，思而不学则殆，可见归类总结在学习过程的重要性.学习数学如果只练不总结，这样学得很累，效果一定不佳，只有在学习的过程中不断总结，才可以迅速提高学习效率，提升解题能力.如函数中有一类关于“任意”和“存在”的问题，这类问题常常体现为“相等”和“不相等(即大于或小于)”问题.通过归类，可用自己的语言总结出解法.如，相等问题可归纳总结为:任意的值域包含于存在之中(详见例7)；不等式问题可归纳总结为:都是任意处理，再将存在改写为其对立面(详见例8).

【例7】设过曲线f(x)=-ex-x上的任意一点处的切线l1，总存在过曲线g(x)=ax+2cosx上的一点处的切线l2，使得l1⊥l2，则实数a的取值范围是

()

A.[-1,2] B.(-1,2]

C.[-1,2) D.(-1,2)

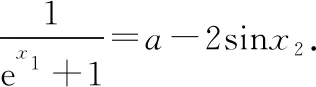
因为-2≤-2sinx2≤2，所以a-2≤a-2sinx2≤a+2.

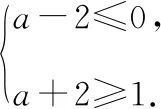
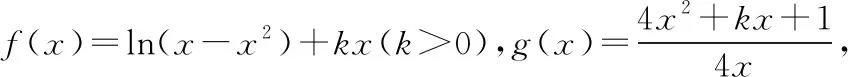
显然，通过以上归纳总结，降低了处理此类问题的难度，并且使学生能够轻松掌握，达到事半功倍之效.

三是要纠错.会学习的学生，基本上都有个错题本.学生们在做数学练习题时，只注重做新的练习题，而忽略反思平时做错的题目，好多学生根本没有记错题的习惯.实际上，将易错问题利用错题本记录下来，经常演练，反复思考，可以有效避免以后再出现类似的错误！

错因探究:太大意啦，只注意到△ABC，而没有考虑它是锐角三角形.

错因探究:虽然细心、认真，但还没有达到足够的细心、认真，没有充分利用一个三角形为锐角三角形的充要条件.

反思感悟:(1)本题极易出错，不但要对cosA+sinC准确变形，而且要准确分析内角A的取值范围.

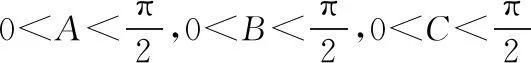
【例10】(Ⅰ)已知0

当然，还可以考虑其他的思路:先消元再放缩；或者对求证式中的“1”先利用题设条件作等量代换，再实施放缩等等.但最终均因没有彻底解决目标问题，而深感无奈！

反思感悟:(1)对于本题第二问，大部分学生的思路可能都是直接针对该问具体分析的，而没有注意考虑第一问与第二问之间的紧密联系，即缺乏灵活运用“联系”的观点去分析、解决问题的思想意识.最终，导致第二问不能顺利获证，认为较难.

(2)由于许多数学解答题设计多问的目的就是降低试题的难度，而各问之间又往往存在着某种紧密的联系，因此将“联系”的观点灵活运用于解题中，往往能够出奇制胜，将问题简洁明了地解决.