基于“隐”圆背景下的一类平面向量模长问题

浙江

1.问题缘起

平面向量模长取值范围问题是平面向量知识的一个重要考查方向.笔者发现这类问题常常会让所求向量的终点落在一个定圆上,但问题表述的过程较为委婉,不会直白地指出这个圆的存在,给我们分析问题解决问题增加了难度.下面笔者就自己的解题感受,来谈谈如何把背后的“隐”圆找出来,进而窥视一下命题者命题时的想法.

2.平面几何刻画下的四类“隐”圆

在平面几何中刻画圆有四种方法:第一是到定点的距离等于定长的点的轨迹；第二是定线段所对的角为直角,那么直角顶点的轨迹为圆；第三是定线段所对的角为定值,其顶点的轨迹为一个圆,即圆周角和弦长确定,可以确定一个圆；第四是一个凸四边形对角互补,可以产生四点共圆,这个凸四边形可以确定一个圆.平面向量问题中的“隐”圆基本就是四种形式的向量表示,下面分别举例加以说明.

2.1向量模长为定值下的“隐”圆

例题1:(2017年浙江省数学竞赛)已知平面向量a,b,c，满足|a|=1,|b|=2,|c|=3,0<λ<1,若b·c=0,则|a-λb-(1-λ)c|所有取不到的值的集合为________.

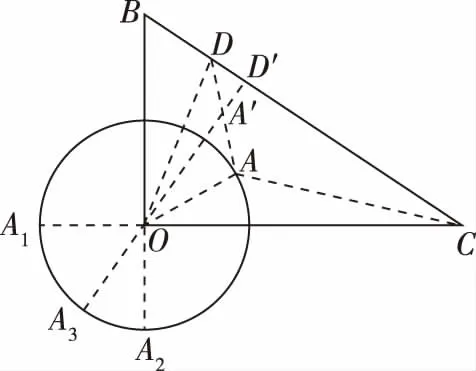
2.2向量垂直下的“隐”圆

例题2:(2018年4月杭州市高三二模第9题)记M的最大值和最小值分别为Mmax和Mmin,若平面向量a,b,c满足|a|=|b|=a·b=c·(a+2b-2c)=2.则

()

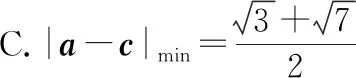
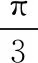
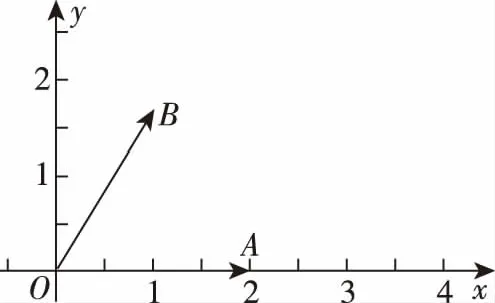
图1

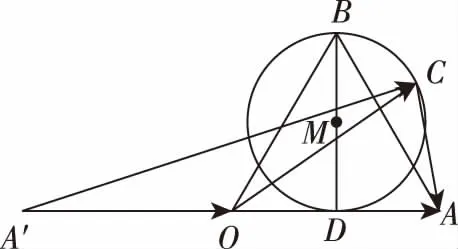
图2

通过条件的代数变化,得到向量垂直的代数结构,确定C点的轨迹为圆,这个圆本质上就是一个直径确定的圆.而我们需要做的是把问题中隐含的几何关系解读出来,那么结果就可以看出来了,下面我们再看一例.

例题3:(2019年1月绍兴上虞高三期末考试填空压轴题)向量a,b,c满足|a|=|b|=|a-b|=c·(2a+b-c)=1,求|c-a|的取值范围为________.

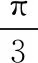
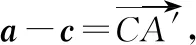
命题者的思维过程无非就是把这个几何结构用向量的代数关系式进行表示,并进行了一定的伪装.

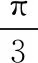
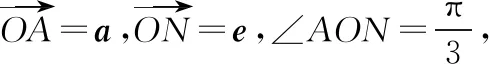
当然我们也可用运算的方式来刻画阿波罗尼斯圆,由条件得|b|2=|2b-3e|2,化简得b2-4b·e+3e2=0,所以(b-e)·(b-3e)=0.

事实上和阿波罗尼斯圆相关的向量代数结构,都可以转化成这样的形式.如果把这个问题中的b2-4b·e+3e2=0写成b2-4b·e+3=0后,就变成了浙江省2018年高考的第9题:

()

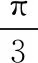
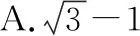
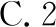
由例题4分析我们知答案为A.

2.3定弦对定角下的“隐”圆

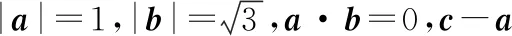
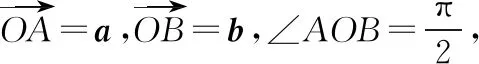
回归到初中的几何知识同弧(弦)所对的圆周角相等.

2.4四点共圆下的“隐”圆

例题6:(浙江省2019学年第一学期五校联考16题)已知向量a,b,c,其中|a-b|=2,|a-c|=1,b,c的夹角为60°,(a-b)(a-c)=-1,则|a|的最大值为________.

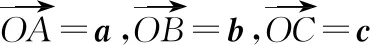
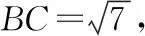
利用四点共圆,结合三角形正(余)弦定理,让我们可以通过简单的计算便可以获得最终的结果,真所谓数形结合百般好.

3.写在最后

事实上“隐”圆是命题者构造问题的几何背景,命题的过程是将这个圆的几何特征用代数的语言来进行描述.对于解题者来说,根据向量的代数关系通过建系用解析法来处理固然可以,但此时重在向量的计算能力的考查.

但如果解题过程中强调数学几何结构背景分析,可以发现以上四类问题共同的“源”是“隐”圆,无非是借助了圆本身蕴含的几种不同的几何性质.解题教学的过程中要借助直觉思维和逻辑推理达成解题者对数学的整体理解,进而实现对数学本质的认识,追求结构体系的至精至简.