连乘积函数求导法则的探究及应用

陕西

对于两个以上函数的连乘积导数问题,通常都是转化为两个函数之积的形式按照积的导数法则求导,或者展开化为多项式函数再求导,这两种思路学生很容易想到,但有时计算量较大,且容易出错.由此引发我们进一步思考:是否有更具操作性的解决连乘积函数求导的法则？于是,笔者在学习了复合函数求导法则后,又引导学生对两个函数之积的求导法则进行了再探究,试图探寻得到两个以上连乘积函数的求导法则,并结合实例进行了应用体验,取得较好效果.

1.两个函数积的求导法则再探究

普通高中课程标准实验教科书《数学(选修2-2)》(以下简称教材)通过特殊探路、合情推理得到了两个函数积的求导法则.

法则1:若两个函数f(x)和g(x)的导数分别是f′(x)和g′(x),则有

[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x).

由于知识所限和教材编排等原因，教材中并没有相应的证明,而是让学生思考能否用导数定义证明法则1.学习了复合函数求导法则后,笔者及时组织学生对两个函数积的求导法则进行了再探究,小组代表向全班交流了思考研讨结果,引起了大家的强烈共鸣.

证明1:设y=f(x)g(x),则由导数定义可得,

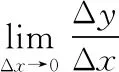
=f′(x)g(x)+f(x)g′(x).

在学生思考分享中,能看出配凑导数定义的变形恰当绝妙,但是还有个别学生对某些细节及求极限的法则不是很理解,为此,我们引导学生走出导数定义的束缚,尝试用教材现有知识加以论证.

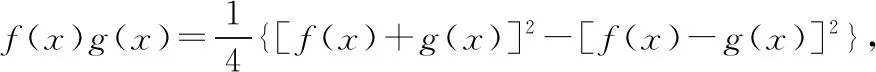
所以由复合函数求导法则可得

证明3:不妨设f(x)>0,g(x)>0,则对y=f(x)g(x)取自然对数得lny=lnf(x)+lng(x),

由复合函数求导法则可得

两边同乘f(x)g(x)得[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x).

评析:证法1依赖于导数定义,证法2、证法3完全依赖于复合函数求导法则.教材虽然是按照先导数的四则运算法则后复合函数求导法则编排,但是借助复合函数求导法则对两个函数积的求导法则的再探究,对加强学生对导数定义、复合函数求导法则的理解和应用大有裨益.

2.两个函数积的求导法则再联想

联想1:观察两个函数积的求导法则结构特点,能否猜测出三个函数积的求导法则？大部分学生认同如下结果.

法则2:若三个函数f(x),g(x)和h(x)的导数分别是f′(x)、g′(x)和h′(x),

则有[f(x)g(x)h(x)]′=f′(x)g(x)h(x)+f(x)g′(x)·h(x)+f(x)g(x)h′(x).

证明1:因为f(x)g(x)h(x)=f(x)[g(x)h(x)],

所以由法则1可得,

[f(x)g(x)h(x)]′={f(x)[g(x)h(x)]}′

=f′(x)[g(x)h(x)]+f(x)[g′(x)h(x)+g(x)h′(x)]

=f′(x)g(x)h(x)+f(x)g′(x)h(x)+f(x)g(x)h′(x).

证明2:不妨设f(x)>0,g(x)>0,h(x)>0,则对y=f(x)g(x)h(x)取自然对数得,

lny=lnf(x)+lng(x)+lnh(x),

由复合函数求导法则可得,

两边同乘f(x)g(x)h(x)得,

[f(x)g(x)h(x)]′=f′(x)g(x)h(x)+f(x)g′(x)h(x)+f(x)g(x)h′(x).

评析:由两个函数积的求导法则引导学生再联想,感悟其中的合情推理、化归转化等思想方法,深刻认识了三个函数积的求导法则.

联想2:能否将法则2推广到更一般的情形呢？我们引导学生大胆猜想得到如下推论.

证明:(1)当n=2时,结论成立；

所以当n=k+1时结论也成立.

由(1)(2)可知,对任意的n∈N*结论都成立.

评析:在三个函数积求导法则探究的基础上,引导学生产生更深入的联想,感悟其中的合情推理、数学归纳等思想方法,让学生深刻认识多个函数积的求导法则,拓宽了学生的视野,有利于提高学生的数学素养.

3.多个函数积的求导法则例析

有了对多个函数积的求导法则的探究,我们及时引导学生在一题多解的练习中进行算法对比,从算法化的高度认识多个函数积的求导法则,减少以往将多个函数积的问题按条件合理组合,转化为两个函数积的求导问题而导致的烦琐和失误.

例1.求下列函数的导数.

对教材的这三个问题进行不同的处理,(1)引导学生利用转化法和直接法进行如下对比:

(2)(3)引导学生利用直接法求导,进一步体会其优越性.

在分组交流环节中,有同学提出(2)也可以先化简再求导,这样运算更简单.

评析:通过分组练习,学生基本熟悉了多个函数积的求导方法,经过讨论也认识到求导之前的化简十分必要.第(3)题留作学生课后练习.

解析1:由法则3可得fn′(-i)=(-i+1)(-i+2)·(-i+3)…[-i+(i-1)][-i+(i+1)]…(-i+n),

从而f100′(-2)=-1×1×2×3×…×98,

又f100(0)=100!,

解析2:令gn(x)=(x+1)(x+3)…(x+n),则f100(x)=(x+2)gn(x),从而有

f100′(x)=gn(x)+(x+2)gn′(x),

所以f100′(-2)=g(-2)=-1×1×2×3×…×98,

又f100(0)=100!,

评析:此题属一次因式连乘积函数,可直接用法则3求导再求值,也可根据一次因式的数据特征转化为两个函数积的形式求导,从而引导学生理解法则3的本质.

之后,我们用变式练习对学生掌握情况进行了限时检测,正确率达98%以上,解答中方法多样,直接使用连乘积函数求导法则的较多,还有根据问题特点设置辅助函数转化为两个函数积的形式,达到了简化运算的目的,显现出了对连乘积函数求导问题的灵活处理.

变式:(1)已知函数f(x)=x(x-1)(x-2)(x-3)(x-4)(x-5),求f′(0).

(2)设f(x)=x(x+1)(x+2)…(x+n),求f′(0).

解析:(1)f′(x)=(x-1)(x-2)(x-3)(x-4)(x-5)+x[(x-1)(x-2)(x-3)(x-4)(x-5)]′,所以f′(0)=-120.

(2)令g(x)=(x+1)(x+2)…(x+n),则f(x)=xg(x),f′(x)=g(x)+xg′(x),所以f′(0)=g(0)=n!.

例3.已知f(x)=(x2-3x+2)(x2+ax+b),若y=f(x+3)是偶函数,且函数y=f(x)+m有4个零点,试求m的取值范围.

解析1:由题意可知,x=1,x=2是f(x)的两个零点,且f(x)图象关于x=3对称,所以x=5,x=4也是f(x)的两个零点,从而有

f(x)=(x-1)(x-5)(x-2)(x-4)

=[(x-3)2-4][(x-3)2-1]

=(x-3)4-5(x-3)2+4,

f′(x)=4(x-3)3-10(x-3)=2(x-3)[2(x-3)2-5],

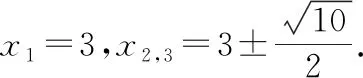
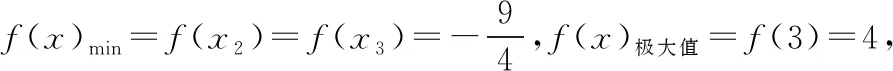
解析2:由题意可知,x=1,x=2是f(x)的两个零点,且f(x)的图象关于x=3对称,所以x=5,x=4也是f(x)的两个零点,从而有f(x)=(x-1)(x-2)(x-4)(x-5),由法则3可得,

f′(x)=(x-2)(x-4)(x-5)+(x-1)(x-4)(x-5)+(x-1)(x-2)(x-5)+(x-1)(x-2)(x-4)

=(2x-6)(x-1)(x-5)+(2x-6)(x-2)(x-4)

=2(x-3)[2(x-3)2-5].

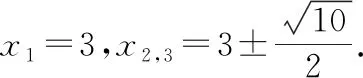
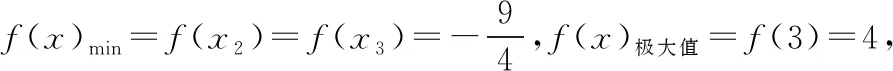
解析3:由题意可知,x=1,x=2是f(x)的两个零点,且f(x)的图象关于x=3对称,所以x=5,x=4也是f(x)的两个零点,从而有

f(x)=(x-1)(x-5)(x-2)(x-4)=[(x-3)2-4]·[(x-3)2-1]=(x-3)4-5(x-3)2+4,

令(x-3)2=t(t≥0),则由题意可知t2-5t+4+m=0有两个正实根,

评析:要求得m的范围,就要搞清楚f(x)的变化趁势和极(最)值,然后考虑以形助数解决问题.其中的关键是一次因式连乘积函数求导,可直接用法则3求导,这是基于算法化理念的认知规律的应用.当然,也可根据一次因式的数据特征转化为两个函数积的形式f(x)=[(x-1)(x-5)]·[(x-2)(x-4)],再根据两个函数积的求导法则求导,这是基于教材知识灵活应用的通法.比较而言,解析2明显好于解析1,而解析3通过换元将问题直接转化为一元二次方程区间根问题,其充要条件也易于求得,避免了连乘积的高次函数求导之忧.可见,多角度审视数学问题,引导学生深刻领悟本题所蕴涵的函数与方程、数形结合、化归与转化等思想方法,不仅有利于提升学生核心素养,而且有利于发挥数学问题的教育价值.

事实上,从算法化理念看,连乘积函数求导问题可转化为两个函数积的求导问题,然后多次使用两个函数积的求导法则不难使问题获解,这种算法基于教材,学生易于接受,体现了化归与转化的思想方法.同一问题可能会有不同的算法设计,自然会有优劣之分和繁简之别,因此,探寻多个函数连乘积的求导法则,是基于让算法思想统领数学学习全程的自然需求,也是算法优化的具体步骤.