圆锥曲线综合题的解答思路与方法分类例说

山东

圆锥曲线的综合问题主要包括:圆锥曲线中的定点、定值、最值、参数问题和探索性问题,它是解析法的应用,数形结合思想方法的良好体现.圆锥曲线与圆锥曲线的位置关系、圆锥曲线知识的纵向联系、圆锥曲线与三角、函数与方程、不等式、数列、平面向量等知识的横向联系也是圆锥曲线的综合问题的重点内容.解决此类问题的分析思想与方法是可循的,重要的是要善于掌握圆锥曲线知识间的横向与纵向联系,解答这部分试题,需要较强的代数运算能力和图形认识能力,要能准确地进行数与形的语言转换和运算、推理转换,并在运算过程中注意思维的严密性,以保证结果的完整.解决圆锥曲线综合题,关键是熟练掌握每一种圆锥曲线的定义、标准方程、图形与几何性质,注意挖掘知识的内在联系与规律.

题型一、圆锥曲线中的定点问题

圆锥曲线中的定点问题往往与圆锥曲线中的“常数”有关,如椭圆的长、短轴,双曲线的虚、实轴,抛物线的焦参数等.解答这类题要大胆设参,推理运算,到最后参数必清.

(1)求E的方程；

(2)证明:直线CD过定点.

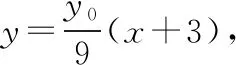
解:(1)依据题意作出如下图象:

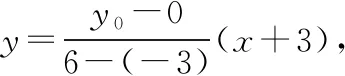
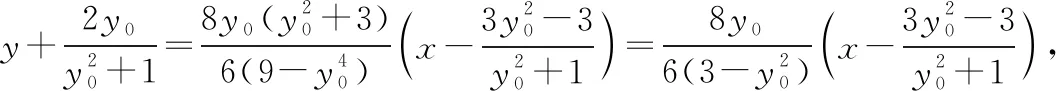
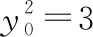
总结提升:

圆锥曲线中定点问题的两种解法:

1.引进参数法:引进动点的坐标或系数为参数,用参数表示变化量,再研究变化量与参数何时没有关系,找到定点.

2.特殊到一般法:根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.

题型二、圆锥曲线中的定值问题

圆锥曲线中的定值问题往往与圆锥曲线中的“常数”有关.定值问题的求解与证明类似,在求定值之前,已经知道定值的结果(题中未告知,可用特殊值探路求之),解答这类题要大胆设参,运算推理,到最后参数必清,定值显现.

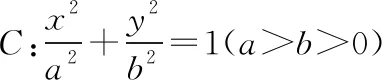
(1)求C的方程:

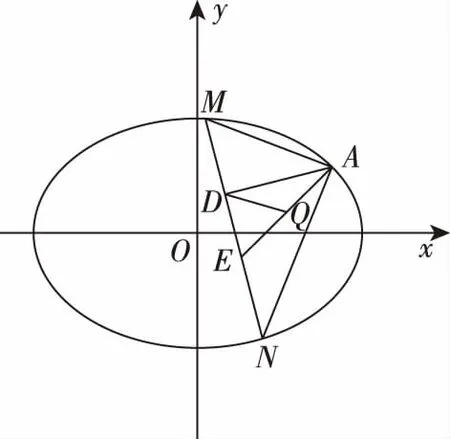
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

分析:(1)由题意得到关于a,b,c的方程组,求解方程组即可确定椭圆方程.

(2)设出点M,N的坐标,在直线斜率存在时设方程为y=kx+m,联立直线方程与椭圆方程,根据已知条件,得到m,k的关系,进而得直线MN恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q的位置.

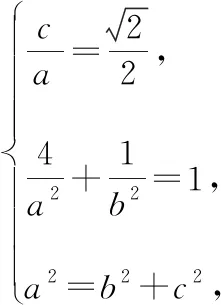
(2)设点M(x1,y1),N(x2,y2).

当直线MN的斜率存在时,设方程为y=kx+m,如图.

将直线MN的方程代入椭圆方程消去y并整理得(1+2k2)x2+4kmx+2m2-6=0,

将y1=kx1+m,y2=kx2+m代入①整理可得(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0.

整理化简得(2k+3m+1)(2k+m-1)=0,

因为A(2,1)不在直线MN上,所以2k+m-1≠0,

所以2k+3m+1=0,k≠1,

当直线MN的斜率不存在时,可得N(x1,-y1),如图.

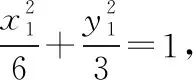
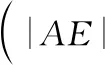
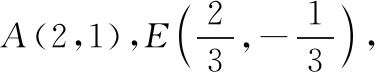
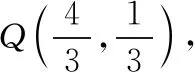
总结提升:

1.圆锥曲线中定值问题的常见类型及解题策略:

(1)代数式为定值:依题意设条件,得出与代数式参数有关的等式,代入代数式,化简即可得出定值;

(2)点到直线的距离为定值:利用点到直线的距离公式得出距离的关系式,再利用题设条件化简、变形求得;

(3)求得某线段长度为定值:利用长度公式求得关系式,再依据条件对关系式进行化简、变形即可求得.

2.两种解题思路

(1)从特殊入手,求出定值,再证明这个值与变量无关；

(2)引进变量法:其解题流程为:

题型三、圆锥曲线中的最值与范围问题

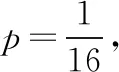
(2)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.

分析:(1)将p代入方程求得抛物线方程即可得到焦点坐标；

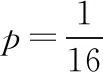
(2)设点A(x1,y1),B(x2,y2),M(x0,y0),l:x=λy+m,

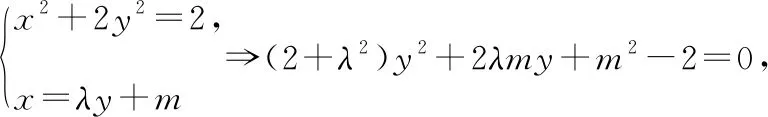
所以y1+y0=2pλ,

所以x1+x0=λy1+m+λy0+m=2pλ2+2m,

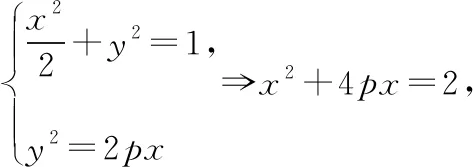
总结提升:

1.处理圆锥曲线最值问题的求解方法

圆锥曲线中的最值问题类型较多,解法灵活多变,但总体上主要有两种方法:一是利用几何法,即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数法,即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解.

2.解决圆锥曲线中的取值范围问题应考虑的五个方面:

(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围;

(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系;

(3)利用隐含的不等关系建立不等式,从而求出参数的取值范围;

(4)利用已知的不等关系构造不等式,从而求出参数的取值范围;

(5)利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.

题型四、圆锥曲线中的探索性问题

【例4】(2019·全国卷Ⅰ文·21)已知点A,B关于坐标原点O对称,│AB│=4,⊙M过点A,B且与直线x+2=0相切.

(1)若A在直线x+y=0上,求⊙M的半径;

(2)是否存在定点P,使得当A运动时,│MA│-│MP│为定值?并说明理由.

解:(1)因为A在直线x+y=0上所以设A(t,-t),则B(-t,t)，

因为⊙M过点A,B，所以圆心M必在直线y=x上，

设M(a,a),圆的半径为r，

因为⊙M与x+2=0相切，所以r=|a+2|；

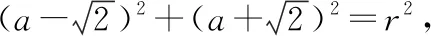
当a=0时,r=2；当a=4时,r=6，

所以⊙M的半径为2或6.

(2)存在定点P(1,0),使得|MA|-|MP|=1,说明如下:

因为A,B关于原点对称且|AB|=4，

所以直线AB为必过原点O的直线,且|OA|=2；

①当直线AB斜率存在时,设AB的方程为y=kx，

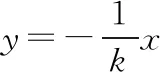
设M(-km,m),⊙M的半径为r，

因为⊙M与x+2=0相切，所以r=|-km+2|；

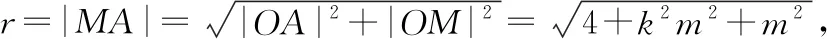
整理可得m2=-4km，

即M点轨迹方程为y2=4x,准线方程为x=-1,焦点F(1,0).

因为|MA|=r,即抛物线上点到x=-2的距离，所以|MA|=|MF|+1，

所以|MA|-|MF|=1，

所以当P与F重合,即P点坐标为(1,0)时,|MA|-|MP|=1；

②当直线AB斜率不存在时,则直线AB方程为x=0，

所以M在x轴上,设M(n,0)，

若P(1,0),则|MA|-|MP|=2-1=1;

综上所述,存在定点P(1,0),使得|MA|-|MP|为定值.

总结提升:

解析几何中存在性问题的求解方法:

1.通常采用“肯定顺推法”,将不确定性问题明朗化,其步骤为:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于特定参数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则(点、直线、曲线或参数)不存在;

2.反证法与验证法也是求解存在性问题的常用方法.

题型五、直线、圆及圆锥曲线的交汇问题

(1)求椭圆C的标准方程；

(2)求点E的坐标.

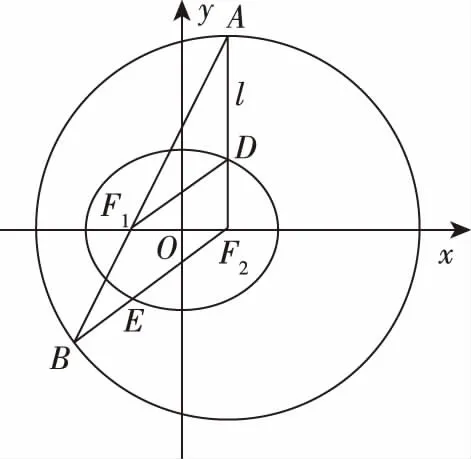
分析:(1)由题意分别求得a,b的值即可确定椭圆方程；

(2)解法一:由题意首先确定直线AF1的方程,联立直线与圆的方程,确定点B的坐标,联立直线BF2与椭圆的方程即可确定点E的坐标；

解法二:由题意利用几何关系确定点E的纵坐标,然后代入椭圆方程可得点E的坐标.

解:(1)设椭圆C的焦距为2c.

因为F1(-1,0),F2(1,0),所以|F1F2|=2,c=1.

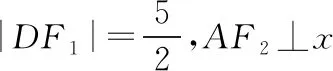
因此2a=|DF1|+|DF2|=4,从而a=2.

因为AF2⊥x轴,所以点A的横坐标为1.

将x=1代入圆F2的方程(x-1)2+y2=16,

解得y=±4.

因为点A在x轴上方,所以A(1,4).

又F1(-1,0),所以直线AF1:y=2x+2.

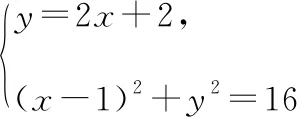
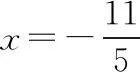
又因为E是线段BF2与椭圆的交点,所以x=-1.

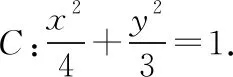
如图,连结EF1.

因为|BF2|=2a,|EF1|+|EF2|=2a,所以|EF1|=|EB|,从而∠BF1E=∠B.

因为|F2A|=|F2B|,所以∠A=∠B,

所以∠A=∠BF1E,从而EF1∥F2A.

因为AF2⊥x轴,所以EF1⊥x轴.

总结提升:直线、圆及圆锥曲线的交汇问题,要认真审题,学会将问题拆分成基本问题,然后综合利用数形结合思想、化归与转化思想等思想来解决问题,这样可以渐渐增强解决综合问题的能力.

题型六、轨迹问题

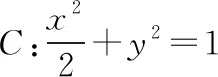
(1)求点P的轨迹方程；

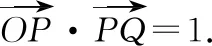
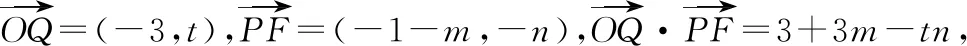
又由(1)知m2+n2=2,故3+3m-tn=0.

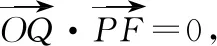
又过点P存在唯一直线垂直于OQ,

所以过点P且垂直于OQ的直线l过C的左焦点F.

总结提升:

求轨迹方程的常用方法:

(1)直接法:直接利用条件建立x,y之间的关系F(x,y)=0;

(2)待定系数法:已知所求曲线的类型,求曲线方程;

(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程;

(4)代入(相关点)法:动点P(x,y)依赖于另一动点Q(x0,y0)的变化而运动,常利用代入法求动点P(x,y)的轨迹方程.