基于落点预测的双旋火箭弹末段飞行控制方法研究
2021-05-28曹小兵徐伊岑常思江钱晓忠
曹小兵,徐伊岑,常思江,钱晓忠
基于落点预测的双旋火箭弹末段飞行控制方法研究
曹小兵1,徐伊岑2,常思江3,钱晓忠1
1. 无锡职业技术学院控制技术学院, 江苏 无锡 214121 2. 无锡商业职业技术学院机电技术学院, 江苏 无锡 214153 3. 南京理工大学能源与动力工程学院, 江苏 南京 210094
针对某双旋火箭弹的末端弹道控制问题,本文提出了一种基于落点预测的弹道控制算法。分析了舵机控制力及控制力矩,建立了该火箭弹的六自由度弹道模型。在匀加速运动假设下,利用三自由度质点弹道方程推导了落点坐标预测解析式及剩余飞行时间计算式,给出了偏差控制方位确定算法,并通过算例仿真分析了不同启控时间和不同控制方位角作用下火箭弹攻角的变化规律,得到了有效控制范围,并针对多个不同目标点应用所设计的控制算法对偏差控制效果进行了计算。结果表明,在有效可控范围内,该控制方法能够有效修正偏差,提高落点精度。
火箭; 落点预测; 飞行控制
火箭弹作为各国军队列装的一种武器装备,在战场上执行面压制、打击敌方重要工事等作战任务,得到了广泛的应用。常规火箭弹在发射及飞行过程中由于受到各种扰动的作用,命中精度较低,而现代战争形势的新变化则对火箭弹的打击精度提出了较高的要求,因此以相对较低的成本对常规无控火箭弹进行适度的制导化改造,以期取得较好的效费比,成为当今弹箭领域技术发展的重要研究方向[1]。
针对火箭弹的制导控制及稳定性等问题,国内外学者开展过相关研究并取得一些成果。张敬敏等人[2]针对单兵火箭,提出了利用捷联激光导引头探测目标位置,并通过脉冲推力器修正弹道的方案。杨靖等[3]以落角作为终端约束,最大化末速作为目标函数,对方案弹道进行了优化。王志刚等[4,5]采用凯恩方法建立了双旋火箭弹的动力学模型,理论分析与仿真结果表明,该模型减少了微分方程的求解数量,同时也能够精确展现弹丸的飞行特性。卞伟伟等[6]基于最优控制理论,应用非线性预测控制方法设计了火箭弹的姿态控制器并分析了控制阶数的影响,结果表明该控制器具有良好的控制效果。贾晓玲等[7]分析了制导火箭弹启控时间对规划弹道的影响,结果表明启控时间对中制导阶段弹箭末速影响比较明显。De Celis R等[8,9]提出一种制导控制算法,利用140 mm火箭弹进行控制仿真,结果表明该算法能够有效大幅减小弹着点散布。Tyan F[10]通过设置约束条件分析了一般比例导引制导律的捕获区域,并通过数值实验证明该技术能够将捕获区域存储在机载火控计算机中。文献[11,12]则通过弹道预测的方法,实现对弹道的修正。
本文以某双旋式火箭弹为研究对象,无控飞行时,带有固定舵的前体相对于后体自由旋转;有控飞行时,前体在反旋电机作用下相对于大地空间静止,固定舵面产生控制力,修正弹道。在弹道末段,利用匀加速直线运动假设,结合三自由度质点弹道方程,建立了解析形式的落点坐标预测模型,推导了剩余飞行时间估算公式,给出了控制力作用方位确定方法,再此基础上通过仿真计算分析了该火箭弹的修正能力,验证了所设计控制方法的可行性和有效性。
1 双旋火箭弹六自由度弹道模型材料与方法
1.1 控制力和控制力矩
控制力由一对同向安装的舵面产生,方向与前体坐标系O1轴平行,用F表示,其表达式如下:

式中,为空气密度,为弹箭速度,为弹箭参考面积,c为舵面升力系数导数,为马赫数的函数,δ为舵面固定舵偏角,δ为总攻角。
将鸭舵控制力F对弹体质心取矩则得到控制力矩,记为M。设舵面压心到弹体质心的距离为l,则有:
M=F·l(2)
1.2 六自由度运动方程组
双旋火箭弹全弹道由滑轨段和自由飞行段组成,其中自由飞行段包括主动段和被动段。本文所研究制导火箭弹在滑轨段和主动段运动方程与常规无控火箭弹相同,被动段则需加入舵控制力及控制力矩的作用。参考文献[11]中所定义的相关坐标系及无控状态下的外力与外力矩,加入舵控制力及控制力矩,即可得到标量形式的质心动力学方程组与绕心动力学方程组
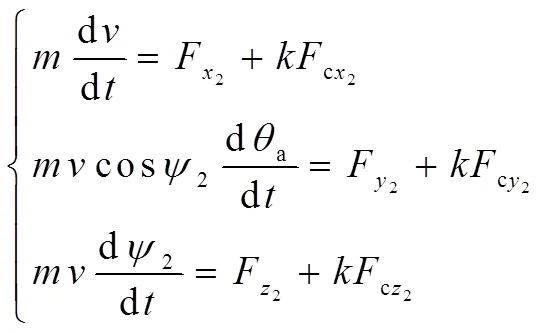
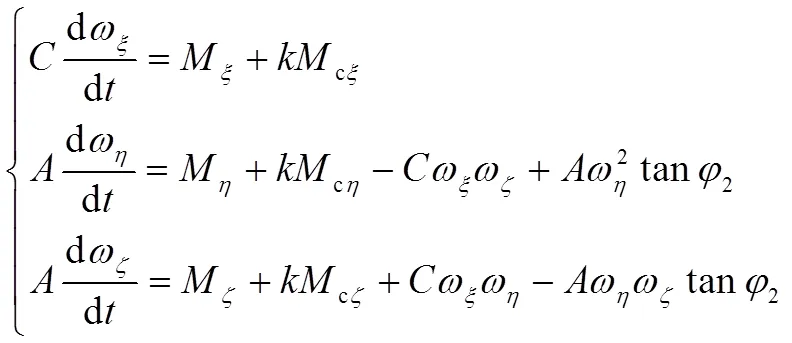
式中,为弹箭质量,θ为弹道倾角,2为弹道偏角,为极转动惯量,为赤道转动惯量,2为弹轴方位角;F2、F2、F2为除控制力外的合外力在弹道坐标系的分量,F2、F2、F2为控制力在弹道坐标系上的分量;ɷ、ɷ、ɷ为弹轴角速度在弹轴坐标系上的分量,M、M、M为除控制力矩外的合外力矩在弹轴坐标系上的分量,M、M、M为控制力矩在弹轴坐标系上的分量;无控飞行时=0,有控飞行时=1。
在方程组(3)、(4)的基础上加入质心运动与绕心运动运动学方程组即可得到完整的双旋火箭弹六自由度弹道模型。
2 落点预测弹道控制算法
出于成本考虑,本文所研究的双旋火箭弹是在弹道末段通过外推方法估算落点坐标,以此与目标点坐标相比较获得偏差大小与偏差方位,从而操纵鸭舵修正弹道,引导弹体飞向目标点。考虑到末段弹道控制的实时性要求,为快速预估落点坐标,此处利用匀加速运动假设,结合三自由度质点弹道方程,可建立落点预测解析模型如下:

式中,m、m、m为火箭弹的预测落点坐标值;、、、v、v、v为预测时火箭弹瞬时弹道诸元;D为阻力系数,t为剩余飞行时间。


求解该一元二次方程,并舍去发散解,可得到剩余飞行时间的估算公式:

设目标点坐标为(x,z),预测落点P与目标点之间有一偏差矢量,如图1所示。在地面坐标系内将该偏差矢量的分量表示为(e,0,e),则有:

为了修正偏差,控制力的作用方位应在偏差对应方位,根据偏差所在方位的不同,可求出所需控制方位角ø的值,如表1所列。

表 1 不同ex、ez对应的øc
3 算例仿真与分析
本文对制导火箭弹的飞行仿真流程为:首先设定目标位置(偏离无控弹道的落点)、发射仰角以及启控时间t。火箭弹发射后,通过比较当前飞行时间和设定的启控时间,判断是否进入有控飞行状态。进入有控飞行后,将每个控制节拍点(0.5 s)的弹道诸元计算值作为实时测量值用于弹道预测,在火箭弹落地之前,采用式和式,输入、、θ、2等参数求解剩余飞行时间,进而利用式和式,输入、θ、2、、、等参数求解火箭弹的预测落点坐标及其与目标的偏差量,最后根据表1查出偏差量所对应的控制方位角ø,据此可计算出作用在火箭弹上的控制力和控制力矩,从而实现对火箭弹的弹道修正。上述过程在每一个控制节拍点上不断重复,直至火箭弹落地。
将上述仿真流程所得落点(含射程与侧偏)与设定的目标位置对比,可验证弹道控制算法的精度。此外,通过记录火箭弹飞行过程中的攻角响应曲线,可对受控条件下制导火箭弹的飞行稳定性进行评估。需要说明的是,上述仿真流程中将计算所得弹道诸元作为弹道测量值,并未人为加入噪声,主要目的是单纯验证弹道控制算法在该类固定舵面制导火箭弹飞行控制中的应用效果。在实际工程中,弹道测量噪声可以通过增加滤波环节予以大幅消除,这一技术已较为成熟,这里不再赘述。
3.1 控制作用下弹道特性与修正能力分析
图2为不同启控时间下攻角变化曲线,t=∞表示无控,仿真条件为θ=45°,ø=0°;图3为不同控制方位角下攻角变化曲线,仿真条件为θ=45°,t=25s;图4为不同启控时间和不同控制力方位角下落点散布图,仿真条件为θ=45°,ø以45°的步长从0°递增。由图2可知,在启控瞬时,攻角变化幅度较大,随后变化幅度逐渐减小,攻角趋于收敛,弹箭运动趋于稳定。由图3可知,在不同的控制方位角下,攻角的变化有所差异,这是因为在不同方位角下,高低攻角和方向攻角的变化趋势不同,从而改变弹箭的运动轨迹。由图4可知,控制方位角不同时,对弹道的修正效果不一致,其落点大致以无控落点为圆心分布;在启控时间不同时,落点分布半径不同,启控时间越早,落点分布半径越大,控制能力越大。

图 2 不同tc下攻角变化曲线
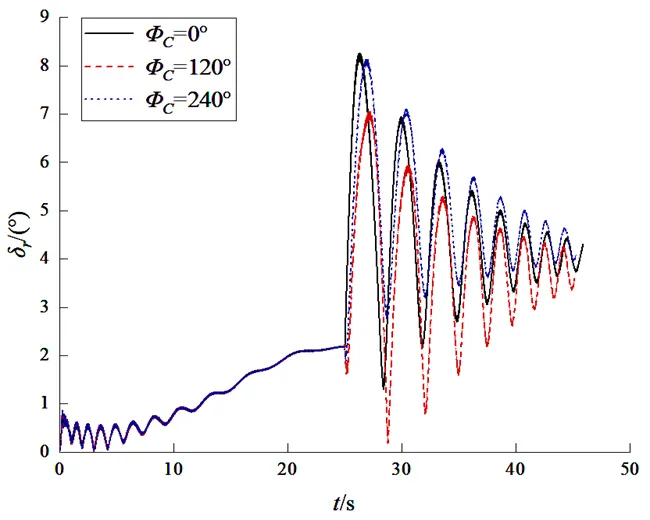
图3 不同øc下攻角变化曲线

图 4 不同tc和øc下落点散布图
3.2 控制精度与弹道特性分析
在弹道控制能力范围内选取任意目标点,采用前文设计的落点预测弹道控制算法进行有控弹道进行仿真,得到了不同目标点下的最终控制效果,如表2所示,其中和表示实际落点与目标点的偏差量。
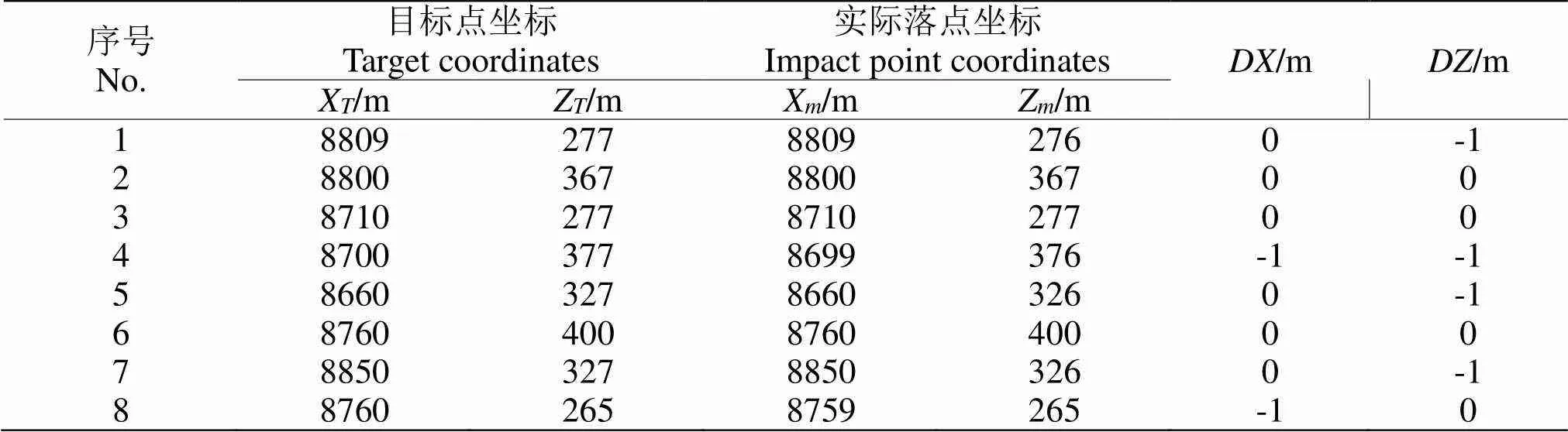
表 2 不同目标点的有控弹道仿真结果
由表2可知,当目标点在弹箭有效控制范围内时,误差范围控制在1 m以内。以目标点1为例,分析其弹道诸元在有控条件下的变化规律。图5为弹箭的攻角变化曲线,图6为弹箭的速度变化曲线,图7为控制力方位的变化曲线。

图 5 攻角曲线

图 6 速度曲线
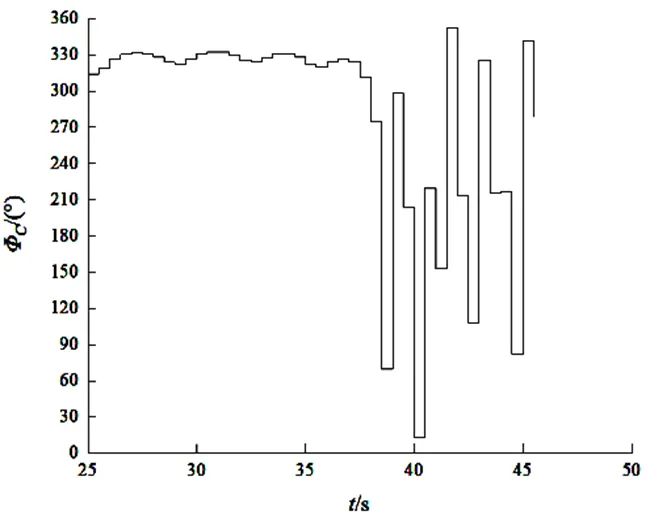
图 7 øc变化曲线
由图5可知,启控之后,弹箭攻角增大,且变化很快,在接近目标点时,攻角变化更快。这是因为在火箭弹飞行过程中不断预测弹道落点并计算偏差量进行姿态调整,越接近目标,对偏差量的估计误差越小,因此控制机构的微小动作也会造成偏差量的增大,鸭舵不断调整控制方向,从而对弹箭的攻角产生很大影响。由图6可知,启控之后速度有所降低,这是因为弹箭攻角增大,飞行过程中的阻力随之增加,从而引起速度减小。由图7可知,在启控之后的初始段,的变化保持在一个定值附近变化,而在接近目标点的末段,ø的变化幅度较大。这是因为初始阶段火箭弹与目标偏差相对较大,在控制的作用下弹箭大致向目标方向靠近,接近目标后,偏差量减小,控制的瞬时作用都会使偏差量增大,此时鸭舵快速调整方向,使偏差量始终保持在较小的状态。
4 结 论
本文通过对某火箭弹进行制导算法研究和仿真分析,得出以下结论:
(1)在弹道下降段,启控时间越早,火箭弹修正能力越强,控制作用使火箭弹攻角产生较大变化,且在不同控制力方位角下攻角变化不同;
(2)在控制算法作用下,火箭弹越接近目标,控制力方位角变化越快,攻角变化越快,速度相比无控减小;
(3)基于弹道预测法设计的控制方法能够使该火箭弹的打击误差限制在1 m量级,具有相当的可靠性和快速性,从一定程度上证明了其可行性和合理性。
[1]陈永超,高欣宝,李天鹏,等.远程制导火箭弹发展现状及关键技术[J].飞航导弹,2016(9):71-74
[2]张敬敏,章浩飞,刘佳兴.一种近程简易制导火箭方案设计和仿真[J].兵器装备工程学报,2019,40(11):40-44
[3]杨靖,毛瑞,杜凤怀,等.基于高斯伪谱法的制导火箭弹总体优化设计研究[J].弹箭与制导学报,2018,38(5):23-26
[4]王志刚,李伟,张振宁.双旋制导火箭弹动力学建模[J].兵工学报,2013,34(7):910-915
[5]李伟,王志刚.双旋制导火箭弹运动特性分析[J].固体火箭技术,2014,37(2):143-149
[6]卞伟伟,王良明,修观,等.制导火箭弹非线性最优预测姿态的控制器设计[J].海军工程大学学报,2013,25(1):59-63
[7]贾晓玲,田晓丽,范旭,等.制导火箭弹起控时间对规划弹道的影响[J].海军航空工程学院学报,2019,34(1):36-41
[8]De Celis R, Cadarso L, Sánchez J. Guidance and control for high dynamic rotating artillery rockets [J]. Aerospace Science and Technology, 2017,64:204-212
[9]De Celis R, Cadarso L. Hybridized attitude determination techniques to improve ballistic projectile navigation, guidance and control [J]. Aerospace Science and Technology, 2018,77:138-148
[10]Tyan F. Analysis of General Ideal Proportional Navigation Guidance Laws [J]. Asian Journal of Control, 2016,18(3):899-919
[11]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014
[12]常思江,曹小兵,刘铁铮,等.基于弹道预测的脉冲修正弹末段控制方法[J].海军工程大学学报,2012,24(6):84-88
[13]普承恩,王良明,傅健.基于EKF落点预测的二维弹道修正弹制导方法[J].兵器装备工程学报,2018,39(6):52-57
Study on the Flying Control Method at Terminal Flight of a Dual-Spin Rocket Based on the Prediction for the Impact Point
CAO Xiao-bing1, XU Yi-cen2, CHANG Si-jiang3, QIAN Xiao-zhong1
1./,214121,2./214153,3./,210094,
A trajectory control algorithm based on the prediction of the impact point was proposed to solve the problem of the terminal trajectory control of a dual-spin rocket. The control force and torque of the canards were analyzed, and the six degrees of freedom equations were established. Under the assumption of uniform acceleration motion, this paper deduced the analytic expressions of the predicted impact point coordinates and the calculation formula of the remaining flight time, based on the three degrees of freedom equations. The algorithm of the control azimuth was given. Simulations for a certain rocket were carried out. The change of the attack angle of the rocket under different start control times and different control azimuths were analyzed. The effective control area was obtained. The control results based on the control algorithm for different assumed targets were presented. The results indicate that the control method can effectively correct the deviation and improve the precision of the impact point.
Rocket; impact point prediction; flying control
TJ765.3
A
1000-2324(2021)02-0308-05
10.3969/j.issn.1000-2324.2021.02.027
2019-01-05
2019-03-06
国家自然科学基金(11402117);江苏省第五期“333高层次人才培养工程”资助(2018Ш-1893)
曹小兵(1982-),男,博士,副教授,主要从事导航、制导与控制相关研究. E-mail:caoxb99@163.com
