基于场论的汽车避撞方法研究

贺启才，蔡少康，王康

（1.中汽研汽车检验中心（武汉）有限公司，湖北 武汉 430056； 2.中国人民解放军陆军军事交通学院汽车士官学校，安徽 蚌埠 233010）

前言

随着先进驾驶辅助系统（Advanced Driver Assistant System，ADAS）的提出，车辆主动避撞技术得到了极大的发展。紧急情况下，系统会通过警示灯来提醒驾驶员采取避撞措施，甚至取代驾驶员完成相应的避撞操作。主动避撞系统通常包括环境感知、信息融合、决策规划和自动控制等方面的内容[1]，其中决策规划层又为四者之重，只有对车辆的安全度进行合理的评价后，才能以此为基础进行后续执行机构的控制。文献[2-4]借鉴人工势场的思想，充分考虑了道路边界和障碍物对行车安全的影响，并建立了对应的势能场，采用最优控制理论和非线性模型预测控制理论对目标函数进行优化，并通过实车试验验证了算法的有效性。文献[5-7]基于APF（Artificial Potential Field，APF）的思想建立车辆跟驰模型，将车辆行驶的环境看作一种场，影响行车安全的各交通因素会对车辆产生引力和斥力，并以此为基础建立关于场能的李雅普诺夫函数，来控制车辆的横向运动。但此种方法仅限于纵向跟车模型，局限性很大。而基于人工势场理论的思想为车辆智能安全技术的研究提供了一种新的思路和方法，只是考虑的交通要素过于单一，难以体现人－车－路闭环系统对行车安全大的影响。

本研究以行车安全场模型作为避撞决策，基于模型预测控制理论，分别建立了避撞轨迹规划控制器和轨迹跟踪控制器，以前轮转角作为控制变量来实现对期望避撞轨迹的跟踪。

1 基于场论的汽车安全评价方法

车辆主动安全决策的评价方法很多，但大部分都是基于纵向临界安全距离来评价，通常只是考虑了车辆自身状态信息以及与周围车辆的相对运动信息等[8-11]。其优点在于模型简单、计算方便，但却鲜少有考虑到人－车－路组成的闭环系统各因素间的相互作用对行车安全造成的影响。因此，“行车安全场”概念[12]应运而生，其充分考虑了交通环境中各交通因素对行车安全度的影响，为车辆智能安全技术的研究提供了一种新的思路和方法。

行车安全场模型主要由交通环境中静止物体形成的势能场、运动物体形成的动能场以及驾驶员心理、行为等各种因素综合形成的行为场组成。其数学模型表达如下：

式中，Es为行车安全场，表示交通环境中各交通因素对行车风险影响程度的大小；ER表示道路上静止物体形成的势能场；Ev表示道路上运动物体（车辆）形成的动能场；ED表示驾驶员行为特性形成的行为场。

物体i（xi，yi）在其周围（xj，yj）处形成的安全场函数如下：

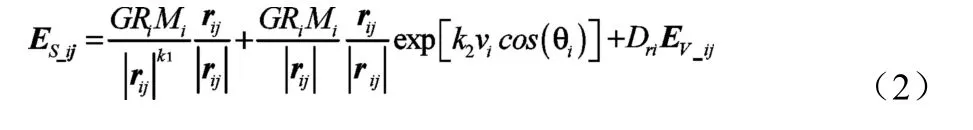
式中：Ri为道路条件影响因子，与道路附着系数、曲率等有关；Mi为等效质量，与物体本身属性、速度等有关；rij为两者间矢量距离；vi为运动物体速度；θi为运动物体速度方向与rij的夹角；G、k1、k2为待定常数。

2 主动避撞控制系统总体结构

汽车主动避撞系统集各种现代高新技术于一体，通过现代传感技术不断增强驾驶员的感知能力，并将获取到的外界信息（包括自身车辆信息与外界车辆、周围环境信息等）实时传递给驾驶员，提醒驾驶员甚至代替驾驶员做出正确的判断和操作。要想实现车辆的主动避撞，就需要实时地获取车辆的行驶状态并做出正确的判断。因此，构建了如图1所示的分层控制结构。基于行车安全场模型的避撞规划层，通过对目标函数的优化求解，得到一系列行车风险最小的轨迹点，并将其拟合作为期望行驶轨迹；下层控制器为对期望行驶轨迹的轨迹跟踪层，以达到避撞的目的。

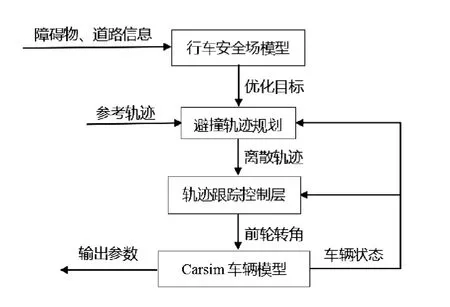
图1 避撞控制结构图

3 避撞轨迹规划与跟踪控制器设计

3.1 避撞规划层控制算法

考虑到避撞规划层的实时性要求相对来说较低，对车辆动力学模型精度要求不高，因此避撞规划层采用点质量[13]模型作为预测模型，参考文献[14]中目标函数的设计，以行车风险最小为优化指标，设计目标函数如下：

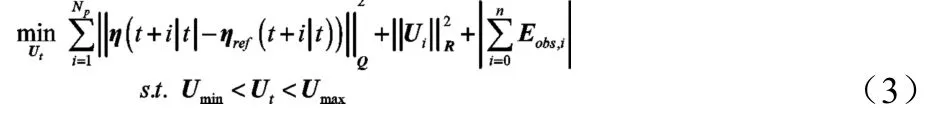
式中，Eobs,i表示i个障碍物形成的行车安全场场强，Q、R均为权重矩阵。

第一项表明在预测时域Np内，将系统的实际输出与参考值进行比较，偏差越小，则表明系统的跟踪能力越强；第二项主要是对控制所需的控制变量的大小进行要求，防止控制变量的大小超出约束范围；第三项是对行车风险的大小进行评估，以获得期望的行驶轨迹。

3.2 轨迹跟踪层控制算法

3.2.1 控制目标的确定

对于一个控制系统而言，控制目标的确定显得尤为重要。选取合适的控制变量，建立能准确描述车辆运动关系的动力学模型是设计控制器的基础。

考虑到太过复杂的模型会大大增加控制算法的计算量，而太过简单的模型又难以体现车辆的动力学特性。因此，建立包括纵向、横向以及横摆三个自由度的车辆动力学模型，如图2。

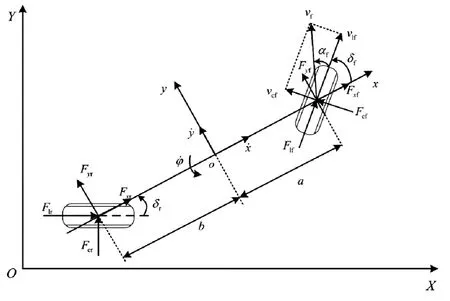
图2 三自由度车辆模型示意图

其微分方程为：

式中，a，b分别为车辆质心到前后轴的距离；m为车辆质量；Iz为车辆转动惯量；φ为车辆横摆角；Fxf、Fxr分别为前后轮胎在x方向的受力；Fyf、Fyr分别为前后轮胎在y方向的受力。

考虑到轮胎力是与轮胎的侧偏角、滑移率、路面附着系数以及垂直载荷有关，而当轮胎的侧偏角与滑移率较小时，对应的轮胎力变化几乎呈线性的，因此经过相应的变换[15]可以得到小角度假设下的车辆动力学模型：

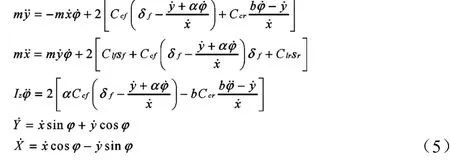
将丄式可转换为状态空间表达式如下：

3.2.2 预测方程

模型预测是一种基于模型的控制方法，因此预测方程是实现算法的基础。考虑到式（5）表达的非线性车辆动力学模型并不适用于复杂车辆动力学控制系统，所以参考文献[16]中的线性化方法对其进行离散处理得到线性离散时变方程：

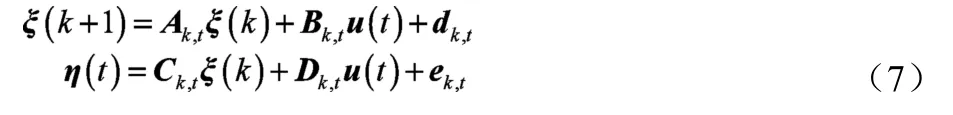
对雅可比矩阵Ak,t、Bk,t求解有：

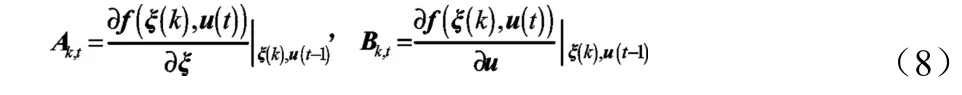
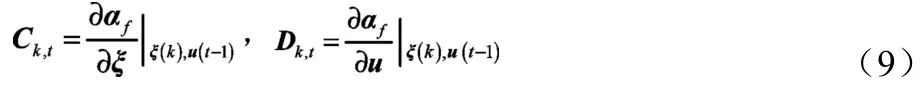
若系统的预测时域为Np，控制时域为Nc，则系统在未来时刻的输出以矩阵的形式表达如下：

式中：

3.2.3 约束优化问题及求解

为了保证轨迹跟踪控制系统的控制性能，需要设定合理的优化目标函数对其进行优化求解，便可达到在控制时域Nc内男足约束条件的有罪控制序列。选取的目标函数表达式如下：

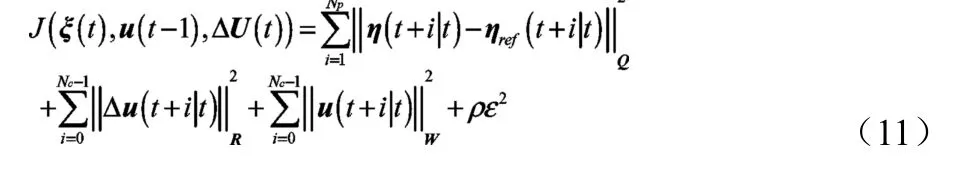
式中，Np为预测时域；Nc为控制时域；Q，R，W均为权重矩阵；ρ为权重系数；ε为松弛因子。

公式（11）第一项表示对期望轨迹的跟踪能力；第二项表示对控制变量增量的大小要求；第三项表示对控制变量极值的要求。

为保证控制性能的最优化，还需要根据实际情况，考虑执行机构的约束条件，对控制变量及其增量施加约束：

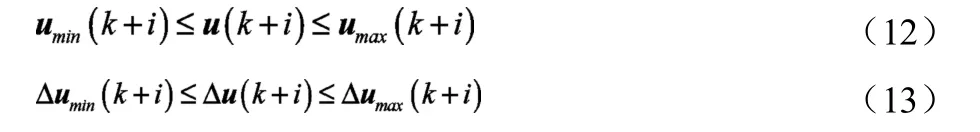
式中，u=[δf]

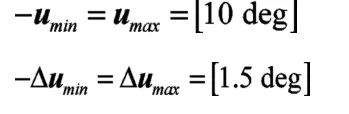
由上述分析可知，这是一个典型的带约束条件的优化问题，可以根据文献[17]转化为标准二次规划问题进行求解。

4 离线仿真结果分析

为了验证所设计避撞控制算法的有效性，基于Carsim与Matlab/Simulink联合仿真平台，在不同障碍物工况下进行了避撞试验。车辆模型基本参数如表1所示，控制器相关参数如表2所示。

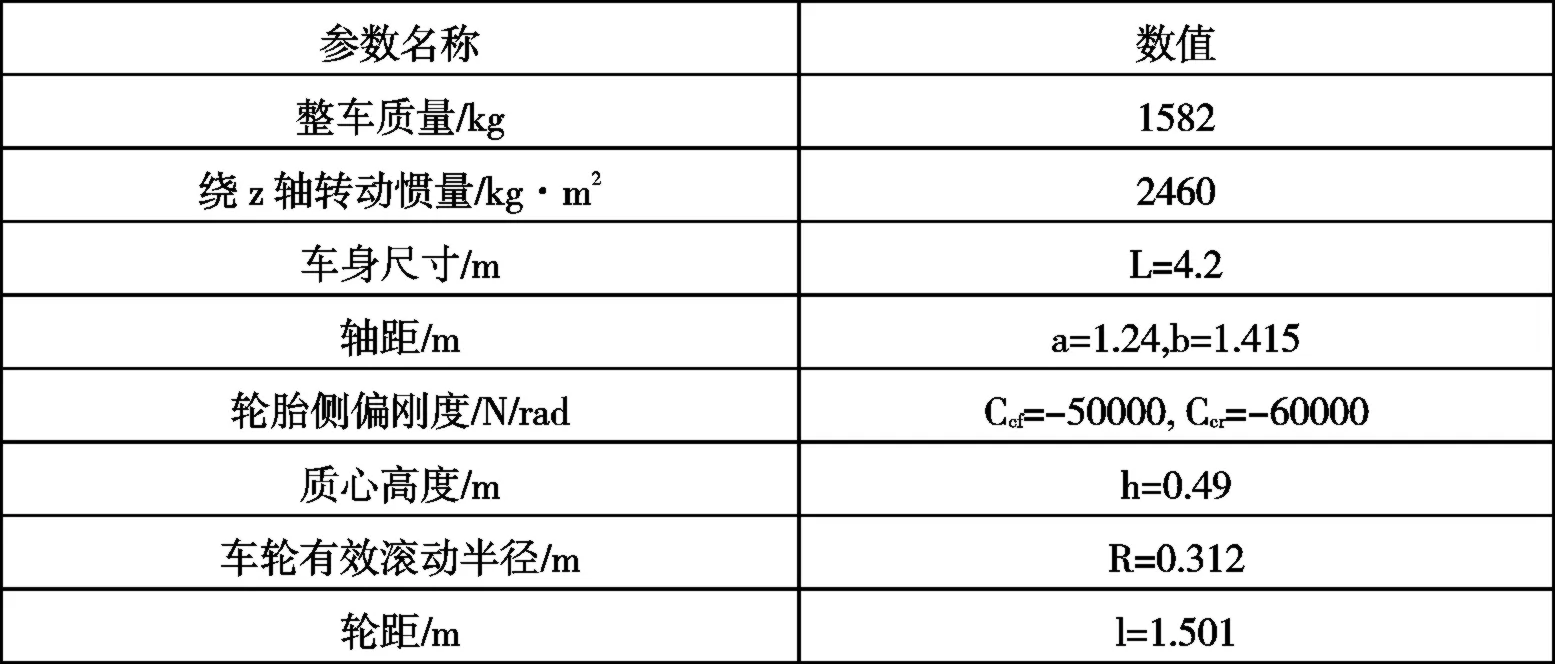
表1 车辆模型主要参数

表2 控制器主要参数

试验工况一：在全局参考轨迹30m处设置1个静止障碍物，角点坐标为（30，0.5），其尺寸大小为5m×2m，势能场参数如下：G=100，RR=1，M=1480，k1=0.5，自车速度为36km/h，道路附着系数μ=0.85。

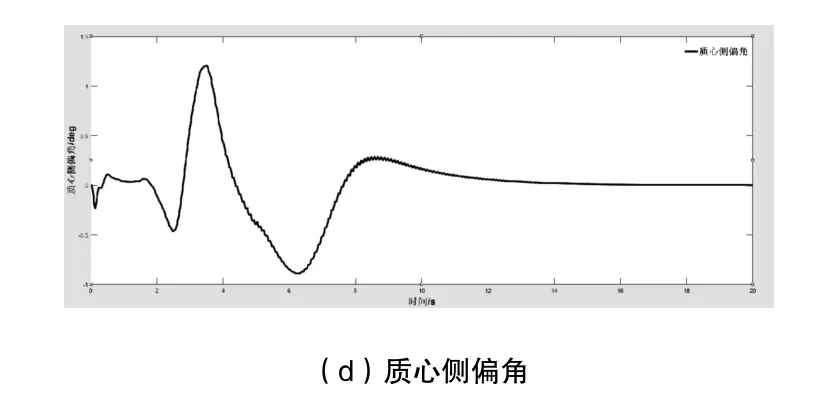
图3 仿真结果

试验工况二：设置障碍物的角点坐标分别为（70，-0.8）、（115，0）、（150，-1.5），尺寸大小分别为5m×2m、5m×0.5m、5m×2m，其中坐标为（115，0）的障碍物为动态障碍物，速度为10m/h，自车速度80km/h，道路附着条件良好。

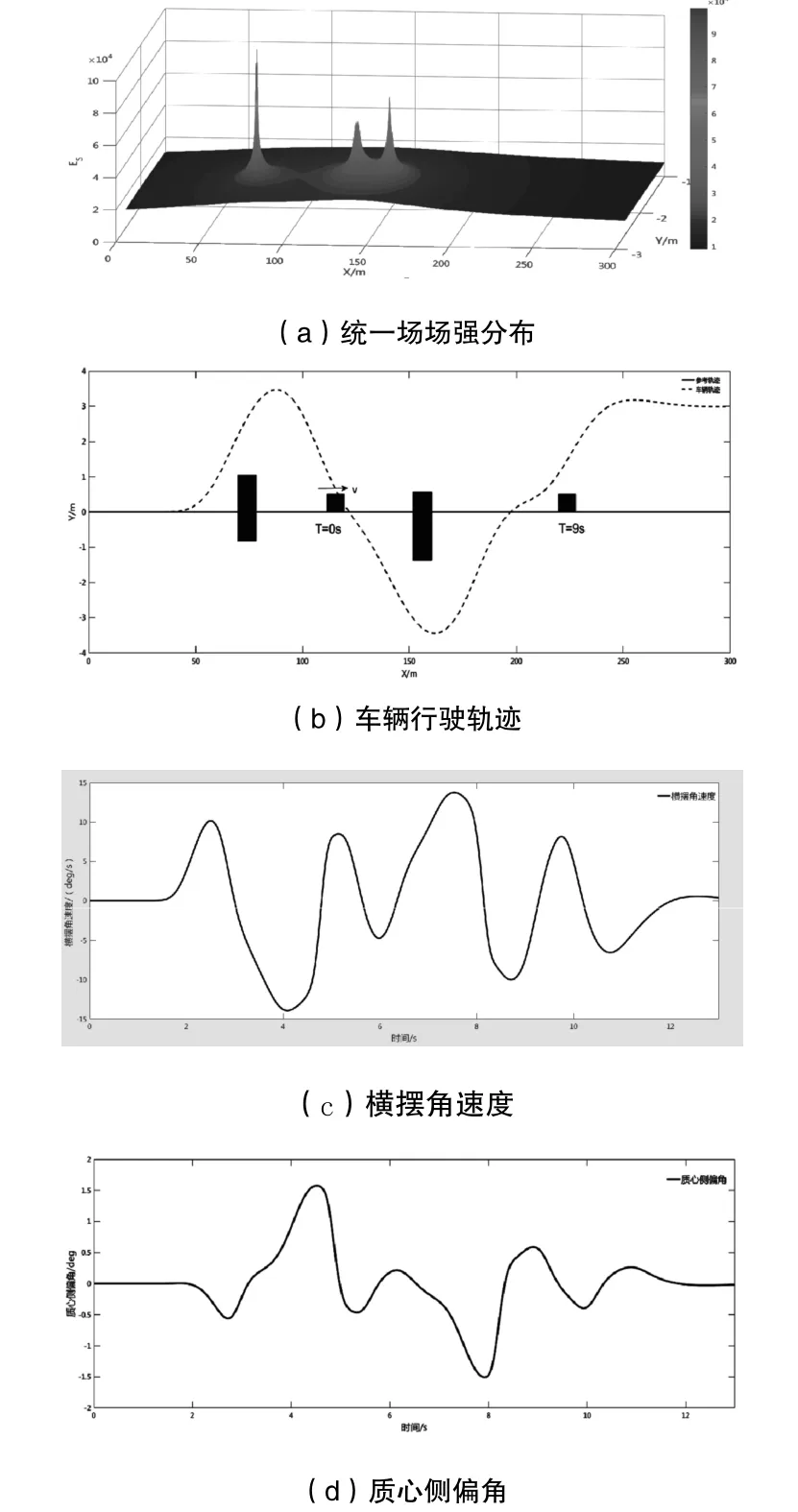
图4 仿真结果

仿真结果如图3、图4所示，（a）为障碍物形成的场强分布，其凸起部分表明了车辆靠近其周围时所具有的行车风险大小，数值越大，表明行车风险越高，那么车辆撞上障碍物的可能性就越大，之所以出现尖端是因为此时已必然发生碰撞，其数值大小是由数学模型决定的。从（b）可以看出，在控制系统的作用下，车辆很好地避开了障碍物。图4中（b），当T=0s时，动态障碍物处于吃屎位置115m，沿直线开始向前行驶；当T=9s，行至205m处，此时车辆位于200m处，开始进行转向操作避撞。从（c）和（d）可知，车辆在避撞的过程中始终保持稳定行驶状态。

5 结论

本文针对带有主动前轮转向的避撞的系统进行了研究，提出了分层控制结构框架，避撞规划层以行车安全场场强为优化指标，基于非线性模型预测控制算法计算求解得到一系列行车风险最小的轨迹点并将其拟合成期望行驶轨迹；下层控制器为轨迹跟踪层，对期望的避撞轨迹进行跟踪。基于Carsim与Matlab/Simulink搭建的仿真平台，结果表明在不同障碍物工况下车辆都能安全稳定避撞。