惯组小系统动力学建模与非线性特性分析

商 霖，张海瑞，赵晓宁

（中国运载火箭技术研究院，北京 100076）

惯组小系统是由惯组、基座和减振器等组成。飞行器飞行过程中，惯组小系统将经历长时大振动、短时强冲击和持续高过载及高温等恶劣环境，严重影响了其测量精度和使用寿命。惯组陀螺信号受外界角振动环境的影响会迭加基座和减振器的角振动分量，导致陀螺测量出现误差，直接影响到飞行稳定性。惯组加表信号受外界线振动环境的影响会叠加基座和减振器的高频振动分量、引入虚假的运动，导致加表测量出现误差，进而影响到导航精度。工程上，通过将基座设计为刚性平台以消除其负面影响，由此惯组小系统线/角传递特性主要取决于减振器环节的合理布局[1,2]和优化设计[3-5]。

减振器作为一种弹性元件，主要用于降低惯组承受的振动和冲击等环境。当前在减振器研究中，往往采用线性化模型进行相关设计和分析[1-6]。实际的减振器是一个非线性的渐软系统，忽略非线性效应的线性化模型不能体现系统的非线性软化特征，也就无法准确地进行非线性特性的研究，甚至导致错误的结果，因此有必要开展惯组小系统非线性动力学建模和非线性特性分析工作。

非线性动力学的研究最早可以追溯到Rosenberg[7]的工作，他提出了非线性模态的概念，奠定了相关理论。Shaw[8]和Nayfeh[9]等相继拓展了非线性模态的定义，推动了该领域的研究发展。Sun[10]等采用复化平均法得到了由简谐外力和非线性能量阱组成的非线性振动系统在稳态响应下的解析解，并通过数值模拟对解析模型进行验证，得到了系统动态失稳的初步认识。Mezghani[11]等提出了一种非线性参数识别方法用于识别非线性振动系统的刚度和阻尼系数。Noël[12]则综述了从2006年来近十年间非线性系统参数辨识领域出现的关键技术，通过讨论实验模型在工程结构设计中的核心作用，为这一领域的发展提供了一个更为广阔的视角。王丹[13]等利用试验结果辨识得到非线性恢复力模型，并将其应用于橡胶减振器的动力学分析。杭超等[14]利用振动台扫频测得了两类橡胶减振器的动刚度和阻尼比。唐安特等[15]采用Mooney-Rivlin 模型和Maxwell 模型叠加组成的非线性粘弹性本构模型计算了橡胶减振器的高频动态特性。

为了研究高量级振动环境对惯组小系统非线性特性的影响，本文将减振器简化成具有立方刚度的三自由度非线性系统，建立了基础激励下的动力学模型，方程中的物理参数取自于真实产品的惯组小系统。随后，采用单自由度激励方式进行惯组小系统传递特性试验，利用仿真模拟结果验证本文非线性动力学模型的正确性。最后，采用龙格-库塔法对不同激励幅值下减振器的非线性动刚度特性进行了数值模拟，采用虚弧长延拓方法给出了不同激励幅值下惯组小系统的非线性频响函数和传递特性及惯组减振器可以适应的飞行振动边界。

1 惯组小系统动力学模型

1.1 模型简化

惯组小系统基本组成如图1所示。其中，将惯组视为刚体；基座处理为刚性基础面；四个减振器（编号分别为1、2、3、4）采用平面四点布局的方式均布在惯组的四个边角，构成整个惯组小系统的减振系统。图1 中，直角坐标系oxyz的坐标原点o位于惯组质心处，惯组质量为4m；坐标轴xyz为过惯组质心的主惯性轴以消除刚体惯性积，其相应的转动惯量分别为4Ix、4Iy和4Iz；四个减振器均简化为无质量的单向弹簧-阻尼元件，其安装位置相对xy和xz面对称，若选用同一规格的减振器，即可实现惯组质心、形心和减振器弹性中心的“三心重合”设计，由此保证了对称面内线、角运动的线性解耦，从而获得理想的减振系统。

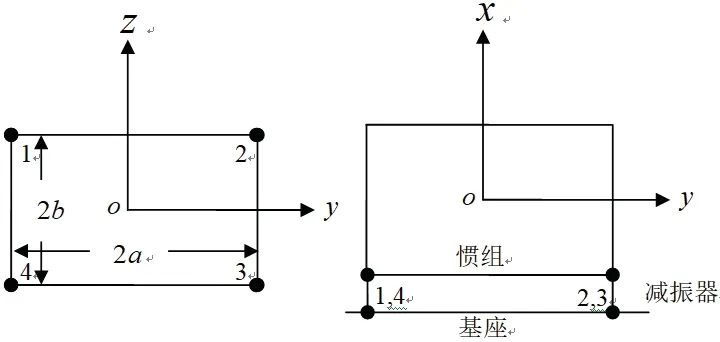
图1 惯组小系统模型Fig.1 The combined model of inertial navigation system

1.2 运动方程

根据飞行姿态需求，仅考虑惯组x垂向、Rz或α俯仰和Ry或β偏航等三个自由度/方向的刚体运动。由此，可令基座的基础激励输入为xi、αi和βi，惯组的刚体响应输出为x、α和β。当基座相对惯组运动时，减振器将阻止这样的运动，按多体动力学方法，则可得到惯组小系统的运动方程：

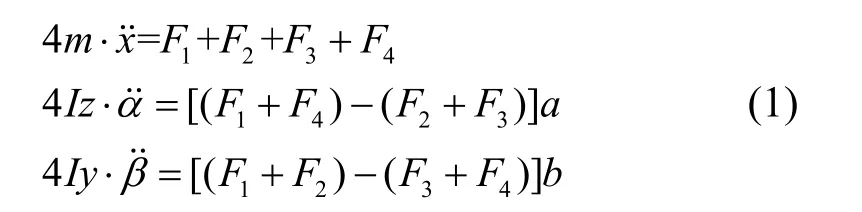
考虑小平移和小转动情况，此时转动是可交换的（即最终位置与转动分量的顺序无关），由此基座和惯组在四个减振器位置的位移就是其平动线位移加上转动角位移的切向分量，可分别表示为：

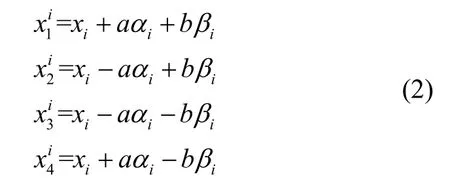
和

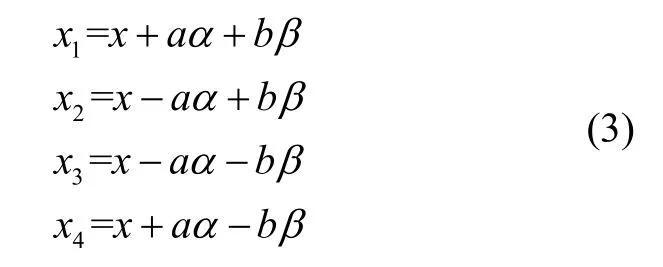
进而，由式(2)和式(3)可以得到四个减振器的变形（且规定压为正），即

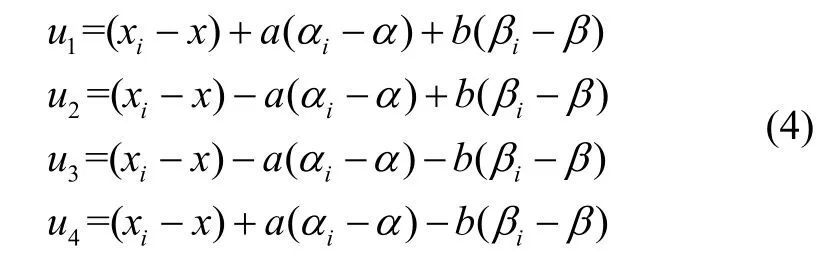
1.3 非线性动力学方程

振动过程中，惯组小系统的减振系统通常选用同一规格的减振器，且严格要求其刚度和阻尼特性保持一致。

因此，这里令ci=c、ki1=k1和ki2=k2，其中i=1,2,3,4。将式(4)代入式(1)可得到如下运动方程：

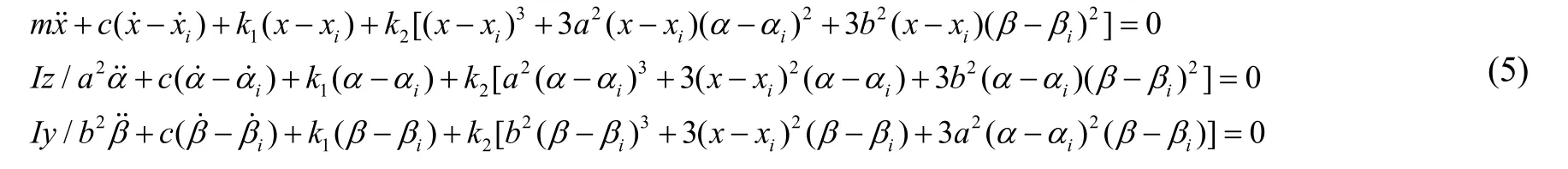
若用xr=x-xi、αr=α-αi和βr=β-βi表示惯组相对于基座的运动，则式(5)可表示为

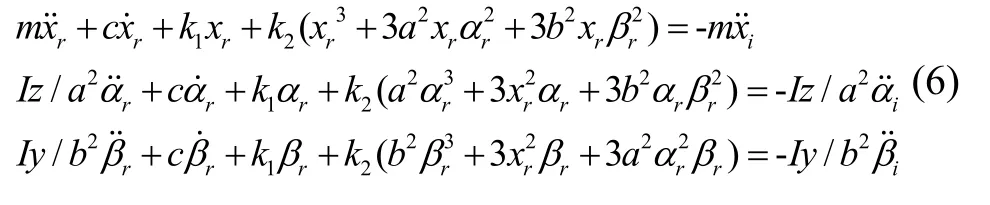
由式(6)所示的含立方项非线性减振器的动力学方程可知，惯组小系统的质量、阻尼和线性刚度项是解耦的，此时若非线性刚度系数k2=0则系统退化为三个单自由度系统，可以独立求解，即实现了线、角振动的分离。若k2≠0则非线性刚度项在线、角位移上引入了耦合关系，k2>0表征为渐硬特性系统，k2<0表征为渐软特性系统。

2 惯组小系统传递特性试验

2.1 试验原理

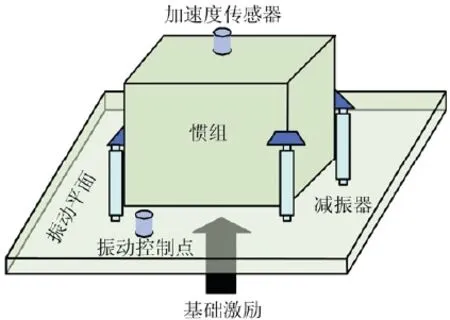
图2 惯组小系统基础激励原理性试验系统Fig.2 Basic excitation principle test system of inertial navigation system

针对某型惯组小系统，工程研制初期搭建了纯线/角振动的原理性试验系统，采用单自由度激励的方式研究其传递特性。如图2所示[16]，惯组通过橡胶减振器连接在振动平台上，电动振动台对振动平台施加正弦扫频激励。振动控制点在振动平台上，通过控制加速度传感器的安装位置和响应量级实现线/角振动的常幅激励。惯组上安装加速度传感器测量减振后信号，或直接采集惯组陀螺或加表的数据。

2.2 试验结果

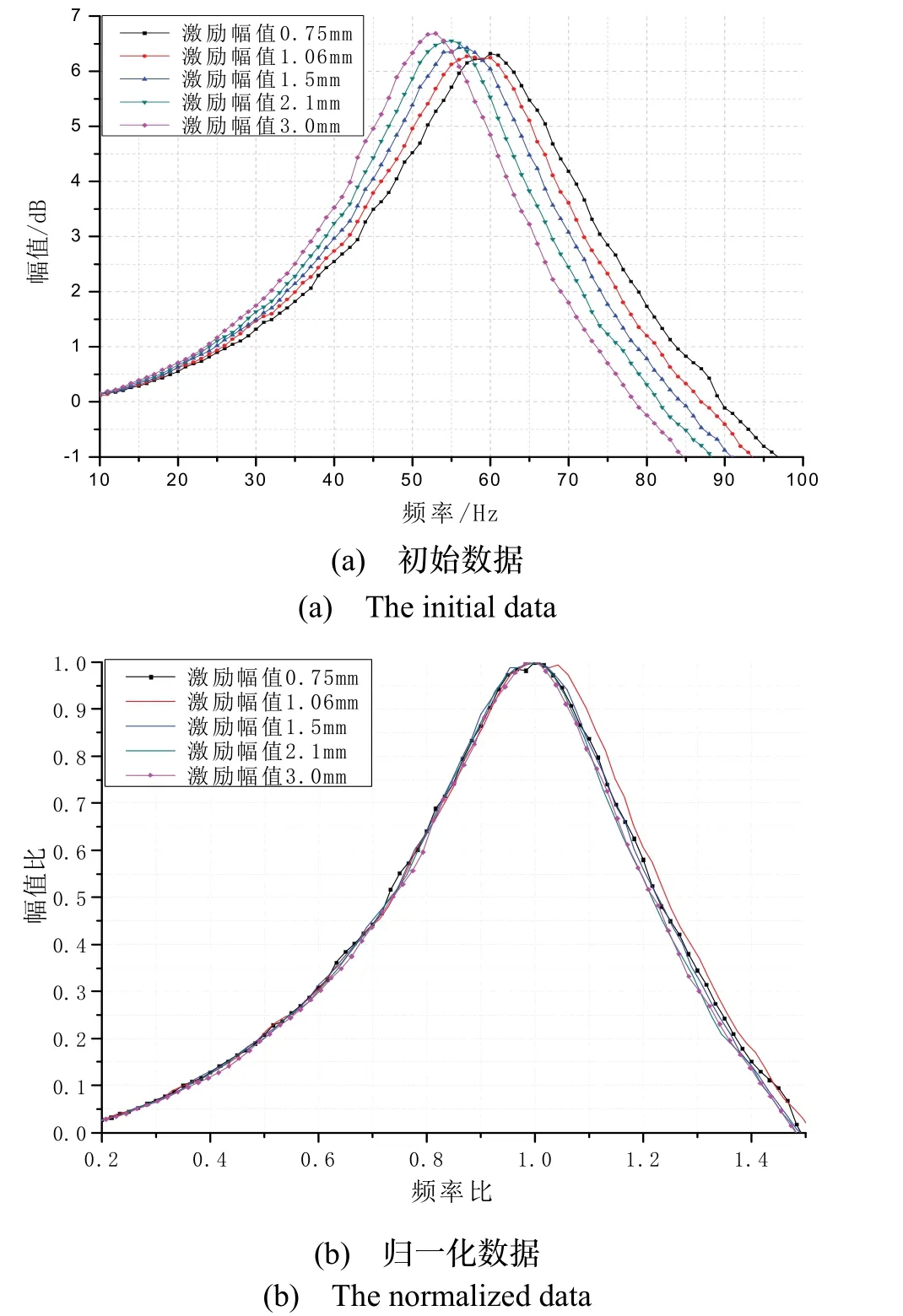
图3 惯组小系统传递特性Fig.3 Transfer characteristics of inertial navigation system

图3 给出了利用正弦扫频激励法得到的惯组小系统线振动传递特性。角振动传递特性试验结果类同线振动。考虑篇幅所限，相关图示略去。图3(a)中，随着激励幅值的逐级增大，系统峰值频率逐渐减小，这表明橡胶减振器呈现出含有渐软刚度的非线性特征。通过对图3(a)中不同激励幅值传递曲线进行归一化处理，即频率相对峰值频率归一化、幅值相对峰值幅值归一化，可以得到图3(b)。

图3(b)中，不同激励幅值下惯组小系统传递特性曲线完全重合，由此表明：1）图3(a)中系统峰值频率的变化，是由于激励幅值的不同导致减振器动刚度不同；2）不同激励幅值下，减振器的阻尼比系数基本不变。

2.3 数值模拟

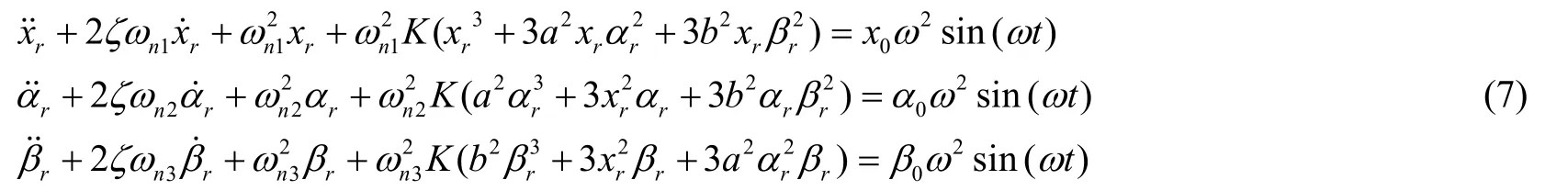
式中，ξ是阻尼比系数，是垂向线频率，是俯仰角频率，是偏航角频率，是刚度系数比，x0是线激励幅值，α0是俯仰角激励幅值，β0是偏航角激励幅值，ω是线/角激励频率。

若模拟纯线运动的正弦激励，则可令x0≠0，而α0=0和β0=0。若模拟纯俯仰的正弦激励，则可令α0≠0，而x0=0和β0=0。同理，也可模拟纯偏航的正弦激励。由此，式(7)中垂向线运动、俯仰和偏航角运动的独立表示可以统一采用如下单自由度非线性运动微分方程

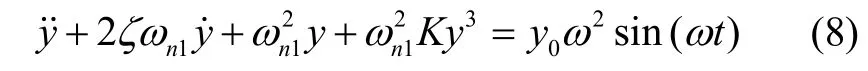
式中，y可分别用于代替垂向线位移xr、俯仰角位移αr和偏航角位移βr。为节省篇幅，下文仅对惯组小系统纯线振动传递特性进行分析。纯角振动传递特性的分析可据此进行。

本文研究中，橡胶减振器的基本参数：线性刚度系数k1=2.15 ×104N/m，非线性刚度系数k2=-3.2 ×107N/m3，阻尼系数c=18.9 N ·s/m ；惯组质量特性参数m=0.16kg 。

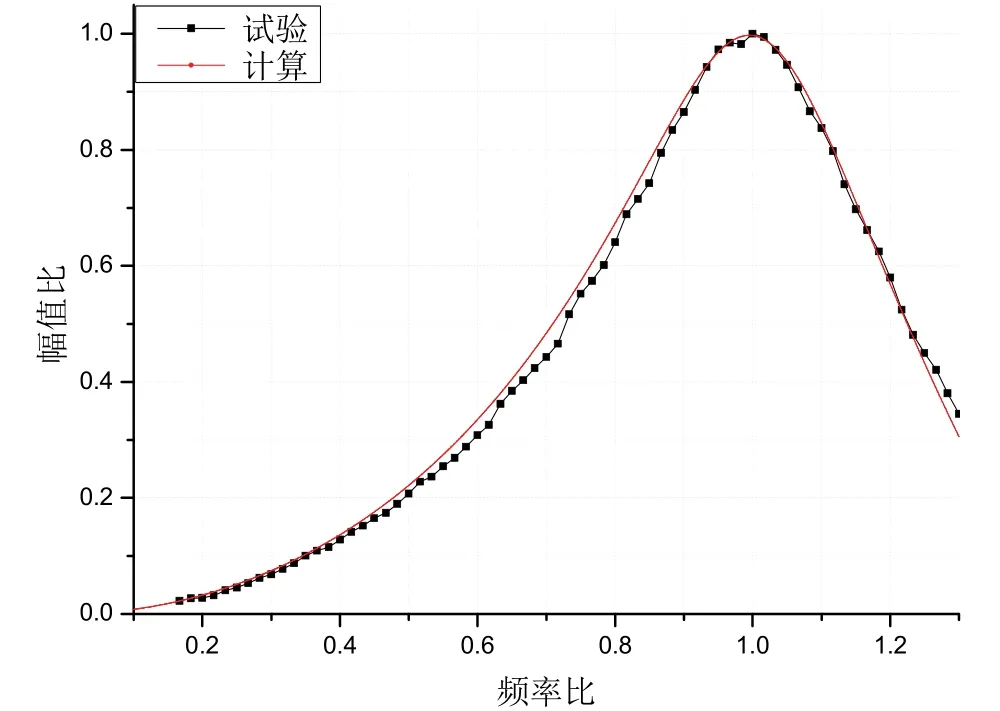
图4 惯组小系统试验结果与数值计算结果的比对Fig.4 Comparison of test results of inertial navigation system with numerical results

图4 给出了采用龙格-库塔数值方法计算式(8)所得数值结果与图3(b)正弦扫频试验结果的对比，二者吻合良好。利用数据统计分析可得，计算结果与试验结果均值偏差仅为1.73%，矢量偏差约1.95%，二者相关度达到了99.9%，吻合度为96.5%。由此表明，惯组小系统非线性动力学模型和模型参数可以真实地表征系统传递特性。

3 非线性特性分析

上文试验结果表明橡胶减振器具有“软弹簧”特性，但缺乏直观的动刚度曲线的验证，也并未真正地表现出非线性动态特性。试验过程中橡胶减振器运动范围在线性、小变形范围内，其力学特性仍是线性的。式(8)中表征橡胶减振器非线性特性的主要参数是刚度系数比K，而诱发这一非线性特性的最直接的因素则是激励幅值y0。下文研究大激励幅值下，橡胶减振器的非线性动刚度特性和惯组小系统的非线性频响函数及传递特性。

3.1 系统动刚度与减振器动刚度

文献[13-15][17]从试验分析、理论推导和数值计算等多个方面研究了非线性系统的动刚度，这些研究工作出发点各不相同，对动刚度的理解和定义也不尽相同。

本文认为惯组小系统包含着两个层级的动刚度，即系统层级的动刚度和橡胶减振器层级的动刚度。系统动刚度包含了惯组质量、减振器刚度和阻尼等，其可表示为

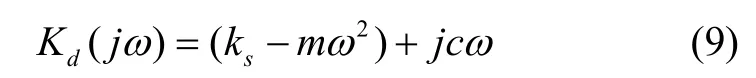
式中，ks为减振器静刚度。橡胶减振器动刚度则由弹性回复力-位移曲线表征，其可表示为

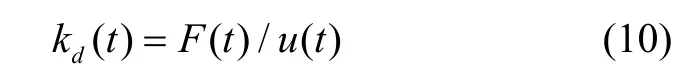
式中，F(t)是减振器的弹性回复力，u(t)是减振器的位移。

采用龙格-库塔积分算法得到式(8)的数值解，并对系统动刚度和减振器动刚度进行分析。计算中，激励幅值y0分别取为0.75 mm、1.5 mm、3 mm、4.5 mm、6 mm 和10 mm 等6 个量级，激励频率ω取值范围为0.1 Hz～120 Hz，扫频速率2 Oct/min。

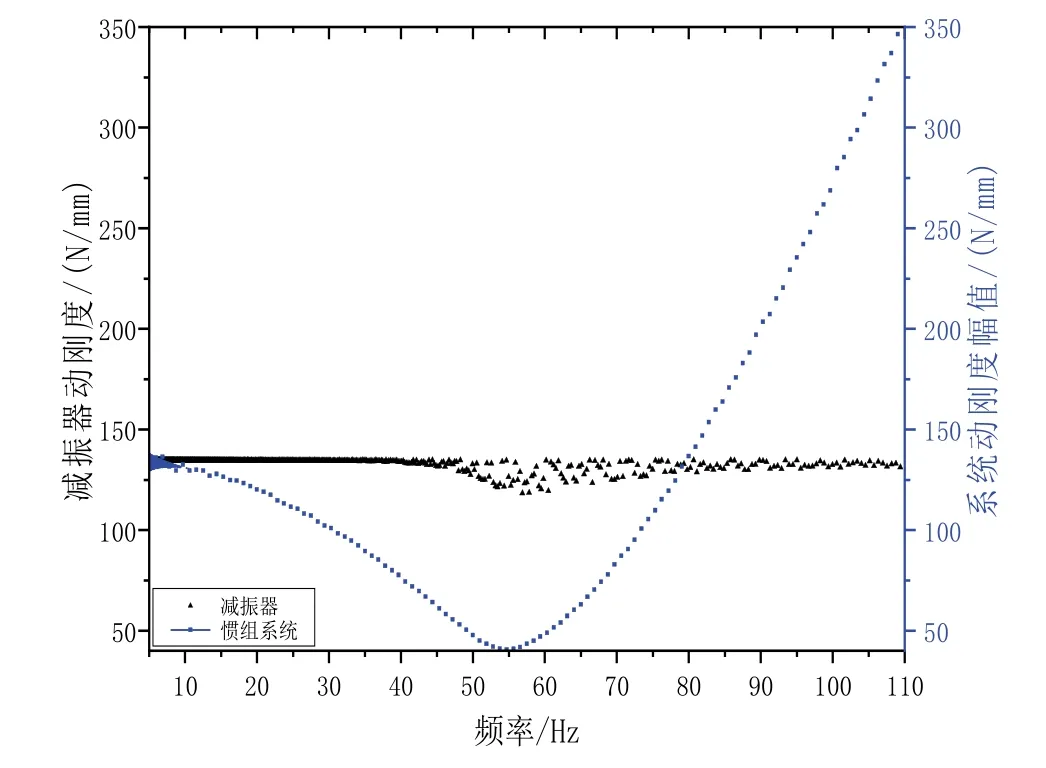
图5 系统动刚度和减振器动刚度的比对Fig.5 Comparison of dynamic stiffness of inertial navigation system and rubber damper

考虑篇幅所限，文中仅从众多计算结果中选出激励幅值3 mm 时系统动刚度幅值与减振器动刚度的比对，如图5所示。从图5 中可看出，相同振幅下系统动刚度随激励频率的变化比较明显，在共振频率点达到最小，表明共振频率附近系统特性主要由阻尼项控制；在低频段动刚度基本等于静刚度，表明共振频率以下系统特性主要由占主导地位的刚度项来描述；在高频段动刚度随激励频率的增加持续变大，表明共振频率以上系统特性主要由占主导地位的质量项来描述。同一振幅下减振器动刚度几乎不受激励频率的影响，在低频段其动刚度接近静刚度，在系统共振频率附近波动明显、相对量较小。已有计算结果还表明，激励幅值越大、波动越明显，但波动规律性不强。

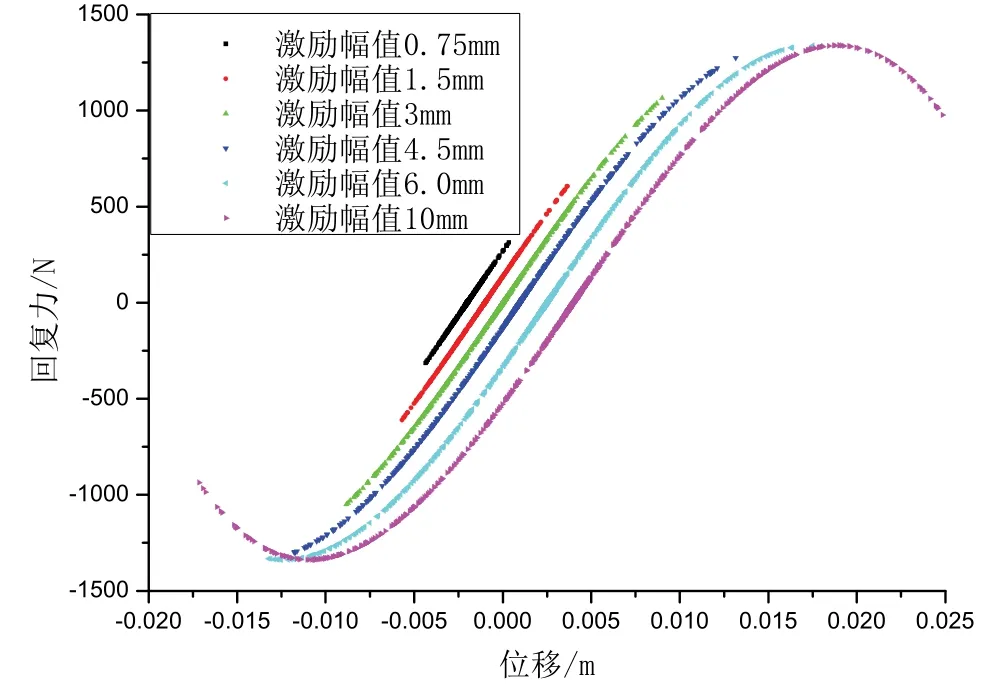
图6 不同激励幅值下减振器回复力-位移曲线Fig.6 Restoring force-displacement curve of rubber damper under different excitation amplitudes

图6 给出了不同激励幅值下减振器回复力-位移曲线的比对。为便于观察，图6 曲线在位移轴方向作了人为的整体移动，即人为改变不同激励幅值下位移零点，简单来说，0.75 mm 激励时位移零点调整为0.001 m，1.5 mm 激励时，位移零点调整为0.002 mm，以此类推。若不作移动，6 个激励幅值下的回复力-位移曲线将完全重合。由图6 可见，激励幅值小于3.0 mm时，载荷-位移曲线近似呈一条直线，表明减振器处于弹性范围内；激励幅值大于3.0 mm 时，随着激励幅值的增加，减振器表现出渐进软化的非线性特性。

3.2 频响函数与传递特性

实际飞行过程中，橡胶减振器不可能仅停留在小变形工况下，大变形工况也是不可避免的。为了探究橡胶减振器在更为严酷飞行环境下的使用能力，了解其特性的稳定性，是否会出现分岔的现象[10,18,19]。本节重点研究不同激励幅值下橡胶减振器的非线性传递特性和频响函数。

针对橡胶减振器这类具有较强非线性特性的系统，传统打靶法在求解其周期解时往往会遇到在分岔点处雅克比矩阵奇异的情况，此时就需要用到延拓算法。本文利用虚弧长延拓方法编制计算程序对式(8)进行求解，获得惯组小系统的传递特性和频响函数，分别见图7 和图8。

计算中，激励幅值y0取值同3.1 节，激励频率ω取值范围为5 Hz～300 Hz。为了区别于传统意义上的扫频试验，这种沿频率范围延拓的方法，可称为数值上的“扫频法”。

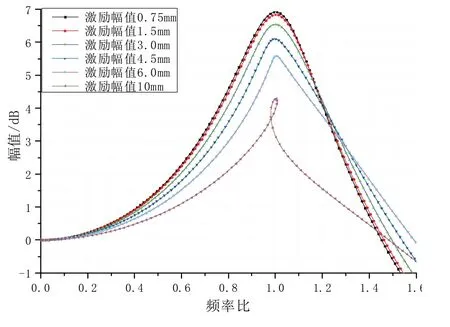
图7 惯组小系统非线性传递特性Fig.7 Nonlinear transfer characteristics of inertial navigation system

图7 计算结果表明，激励幅值3.0 mm 时减振器开始表现出轻微的非线性特性，在非线性范围内激励幅值越大，系统损耗越大、峰值变尖，半功率带宽变小。激励幅值10 mm 时，传递曲线发生了扭曲、变形，形成了一个回路转折点，表明系统特性不太稳定。

图8 中，激励幅值3.0 mm 时，频响曲线的共振峰出现了明显的偏左弯曲，在非线性范围内激励幅值越大，系统的软化特性越明显。对于激励幅值10 mm的情况，当激励频率ω缓慢增加时，振幅沿着曲线上点1、2、3、4、5 变化，并且振幅在曲线上由点3 跳跃到点4，出现了一个激励频率对应两个位移数值解的情况。当激励频率ω缓慢减少时，振幅沿着曲线上点5、4、6、2、1 变化，并且振幅在曲线上由点6 跳跃到点2，此时真实的位移解将依赖于系统的初始状态。两种情况下均发生了系统特性跳跃的现象，即任何微小的扰动都会导致系统响应在两个位移解之间跳跃，说明系统特性已经失稳了。通过数值计算结果分析可知，惯组减振器适应的飞行环境振动位移不应超过3 mm。

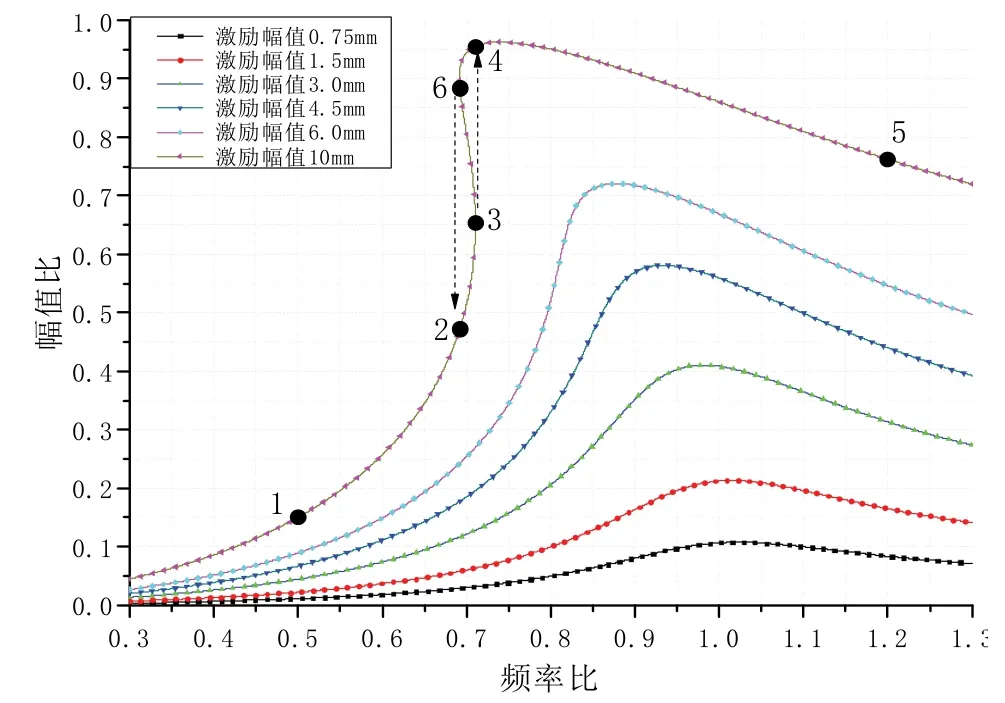
图8 惯组小系统非线性频响函数Fig.8 Nonlinear frequency-response functions of inertial navigation system

4 结论

研究了不同激励幅值对惯组小系统非线性动刚度特性和频响函数及传递特性的影响。基于“三心重合”的设计思想和飞行器的姿态需求，构建了含立方项非线性刚度的惯组小系统非线性动力学方程。采用正弦扫频激励的方式获取惯组小系统传递特性，得到了橡胶减振器动刚度受振幅影响的结论，试验结果验证了其具有渐软刚度的非线性特性。扫频法计算结果与正弦扫频试验结果的吻合度达到了96.5%，检验了非线性动力学模型的正确性。基于构建模型，采用龙格-库塔法计算得到的动刚度曲线直观地表征了减振器的渐进软化的非线性特性，发现了减振器动刚度存在对激励幅值和激励频率的敏感区域。采用虚弧长延拓法通过频响函数和传递特性的非线性分析预示了高量级振动环境下惯组小系统会出现动力失稳的现象。

本文模型工程应用简便，对惯组小系统非线性特性的预示具有较高的精度，供飞行器姿控系统设计时参考。针对大过载飞行环境，建议采用预压缩设计合理调整减振器预压缩量。预压缩设计会影响系统的静平衡位置，通过将坐标系原点选在静平衡位置就可以简化系统运动方程，适当调整本文模型参数即可用于相关环境下非线性特性的预示。

飞行器实际飞行时处于一个多自由度激励的环境，后续建议开展多自由度激励下惯组小系统非线性特性的研究。