一种半球谐振陀螺振幅控制方法

李建朋，武志忠，刘吉利，付明睿，李 恺

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190）

半球谐振陀螺仪是一种具有高精度、长寿命、高可靠性、天然抗辐射的新型固态振动陀螺。迄今为止，半球谐振陀螺已参与小行星登陆、土星环绕、水星探测和深度撞击等宇航空间探测项目，并表现出优异的性能[1,2]。在美国，Northrop Grumman 公司的半球谐振陀螺仪已在超过200 颗航天器上成功应用，在轨运行时间超过5000 万小时，任务成功率100%。在欧洲，Safran 公司新研制的半球谐振陀螺(HRG CrystalTM)已向市场提供超过15000轴，应用覆盖陆海空天领域[3]，在空间应用方面，也有超过100 轴的成功在轨应用[4-6]。

半球谐振陀螺是一种通过哥氏效应来获取检测对象旋转角度或角速度信息的振动陀螺[7]。在该类陀螺中，敏感结构的振动幅度控制是陀螺工作的基础环节，也直接影响陀螺的性能指标。针对半球谐振陀螺的振幅控制环节，文献[8]建立了力平衡模式半球谐振陀螺仪振幅控制稳态模型；文献[9]提出了一种力平衡模式半球谐振陀螺仪振幅控制优化方法。然而，上述文献均未研究振幅控制环节中被控对象模型以及振幅控制启动等内容。

本文针对半球谐振陀螺振幅控制回路设计问题开展研究。首先建立振幅控制回路设计中驱动力与陀螺振动幅度的传递函数，提出被控对象模型；其次针对陀螺如何起振的问题，提出一种半球谐振陀螺的起振方法；然后基于上述的研究基础，设计一种半球谐振陀螺振幅控制回路方案，并对振幅控制闭环回路的传递函数模型进行推导；最后采用数字器件对振幅控制回路进行物理实现，并对实现效果进行评估。

1 振幅控制理论分析

1.1 工作特性

半球谐振陀螺正常工作时，作为敏感结构的谐振子处于四波幅振动状态，谐振子上的振型可以沿相距45 °的两个电极轴（X 轴、Y 轴）进行正交分解和合成。根据文献[10]可知，半球谐振陀螺的数学模型可用式(1)表示：

假设激励电极放置在X 轴上，X 轴为振幅控制轴（驱动轴），分析X 轴的振动特性。在忽略非理想因素的条件下不影响振动特性，将式(1)中的X 轴动力学方程简化表示为：

其中，Q为品质因数，该参数一般大于107，ω为谐振频率，该参数一般为5 kHz 左右。

分析式(3)的频域特性（如图1所示）可知，半球谐振陀螺正常工作时，陀螺是在谐振频率点工作，而不是一个频率范围内工作，如图1 中工作点，该工作点的相位滞后90 °。基于半球谐振陀螺的“点”工作特性，陀螺要正常工作需要一种启动方法让陀螺从静止状态过渡到正常工作的谐振点上；本文第1.3 节将针对这个问题提出一种半球谐振陀螺的启动方法。

此外，根据图1 还可知，半球谐振陀螺驱动轴的幅频特性与带通滤波器的特性一致，因此可将半球谐振陀螺驱动轴频域特性理解为选频网络，在振幅控制回路设计中可以利用该特性。

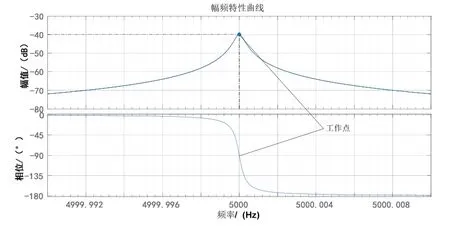
图1 半球谐振陀螺驱动轴幅频特性示意图Fig.1 Amplitude-frequency characteristic of driving axis for Hemispherical Resonator Gyro

在力平衡工作模式下，半球谐振陀螺振幅控制回路的作用是将X 轴（驱动轴）维持在恒定幅值振动。

假设X 轴的振动方程为：

在力平衡工作模式下，0y=，同时忽略振型频率差、离心力等因素，根据式(1)，可知陀螺输出为：

陀螺的标度因数为：

由式(6)可知，在力平衡工作模式下，驱动轴的振动幅度与陀螺标度因数成正比关系，振动幅度控制的稳定性直接决定陀螺标度因数的稳定性，因此陀螺振幅控制的稳定性是评价振幅控制回路设计优劣的核心指标。

1.2 控制对象模型

根据上节可知，半球谐振陀螺正常工作时，陀螺工作在谐振频率点而非一个范围，本节将推导驱动力到陀螺振动幅度的传递函数模型，为振幅控制回路的设计提供理论基础。

在不影响推导结果的前提下，暂不考虑频差和阻尼不均匀性等非理想因素，假定驱动力为：

其中，F为驱动力幅度，为驱动力频率。

将式(7)代入式(3)，可得

求解微分方程(8)可得:

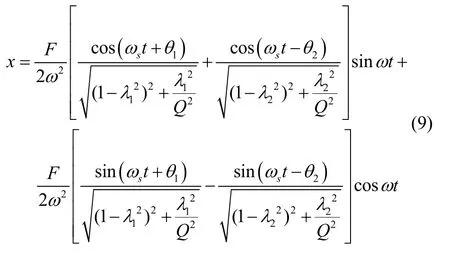
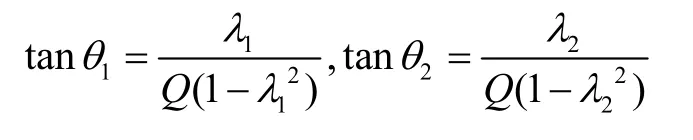
半球谐振陀螺正常工作时，频率跟踪回路将陀螺驱动工作在谐振频率点，振幅控制中信号处理采用“解调”模式，利用频率跟踪回路提供的参考信号对公式(9)进行幅值解调，可得：

其中，

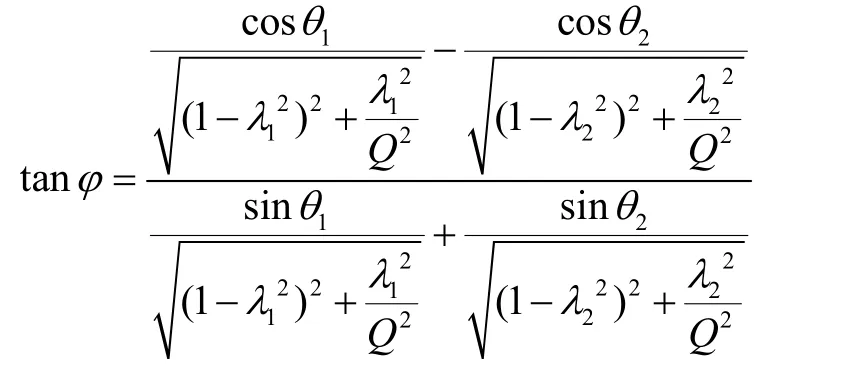
根据公式(7)假设条件和公式(10)可知，驱动力与陀螺振动幅度的幅频和相频特性为：

根据幅频特性和相频特性与系统模型的关联性，可知驱动力与陀螺振动幅度的传递函数为：

1.3 扫频起振方法

通常，振动陀螺的起振方法有自激振荡法、锁相环法等方法[11]。本文针对半球谐振陀螺高品质因数（Q值）的特性，提出一种基于高品质因数值特性的扫频起振方法。

半球谐振陀螺的敏感结构谐振子采用高品质因数的熔融石英材料加工而成，同时谐振子被密封在高真空度的密封腔体内，因此谐振子的品质因数极高，一般可达107。

根据式(12)可知，

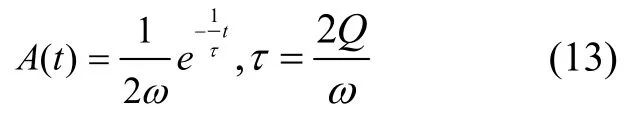
半球谐振陀螺的振动幅度A0自然衰减到A0/2.718的时间为：

半球谐振陀螺极低的能量衰减率和超长的衰减时间是本文扫频起振方法的基础之一。

从1.1节的半球谐振陀螺驱动轴的幅频特性可知，半球谐振陀螺具有很好的选频特性，该特性是本文扫频起振方法的基础之二。

本文提出的半球谐振陀螺起振方法类似于敲击“酒杯”（谐振子）的方式，本质是利用共振原理。根据式(3)，假定驱动力为：

可知式(3)的稳态解为：

本文提出的扫频起振方法的流程图如图2所示，在起振控制流程中，以一定的步进频率步长（fΔ ）激励陀螺，当激励信号频率完成一次扫频范围后，进行陀螺起振状态检测，如果此时陀螺已经起振，则进入振幅闭环控制；如果没有起振，则循环上述过程，直到陀螺启动。

陀螺起振检测方法，采用幅度和频率双元检测方法。只有当幅度和频率均满足以下条件时，才判定陀螺已起振。

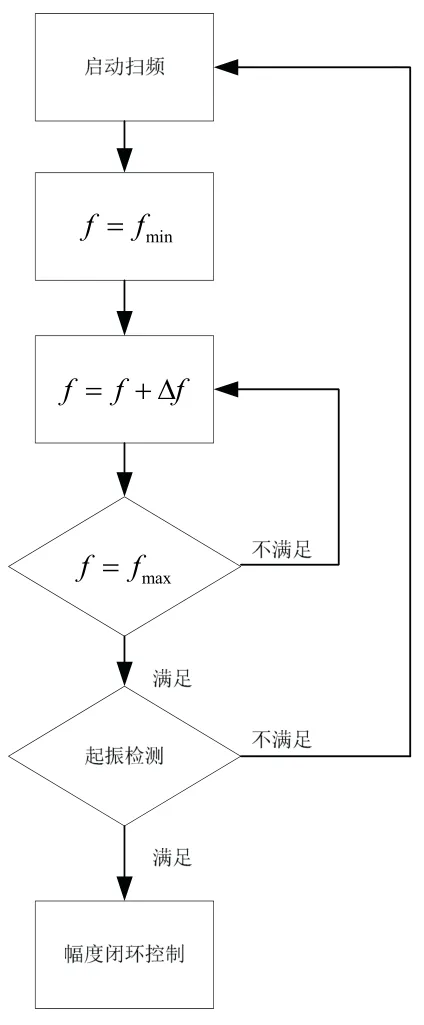
图2 陀螺起振流程图Fig.2 Flow chart of starting vibration for gyroscope

2 振幅控制方案及设计

根据上节的分析与推导，本文针对半球谐振陀螺的振幅控制，设计一种陀螺的振幅控制回路方案，如图3所示。

图3 半球谐振陀螺幅度控制方案框图Fig.3 Block diagram of amplitude control for hemispherical resonator gyro

本文设计的半球谐振陀螺振幅控制方案由两部分构成，一是陀螺起振控制部分，另一是陀螺振动幅度稳定控制回路。陀螺起振控制部分采用本文1.3 节提出的方法实现；陀螺幅度稳定控制回路以式(12)作为被控对象，控制回路包括信号预处理、信号解调和PI控制等部分。

半球谐振陀螺振动检测采用电容检测方式，检测电容可近似用平板电容表示，该环节的传递函数为：

振动敏感信号处理采用“解调”模式，半球谐振陀螺振动检测信号解调增益为：

半球谐振陀螺驱动激励采用静电电容方式，该环节的传递函数可表示为：

根据图3 和幅度控制回路中各环节的数学模型建立幅度控制回路传递函数方框图，如图4所示，控制器采用PI 控制。

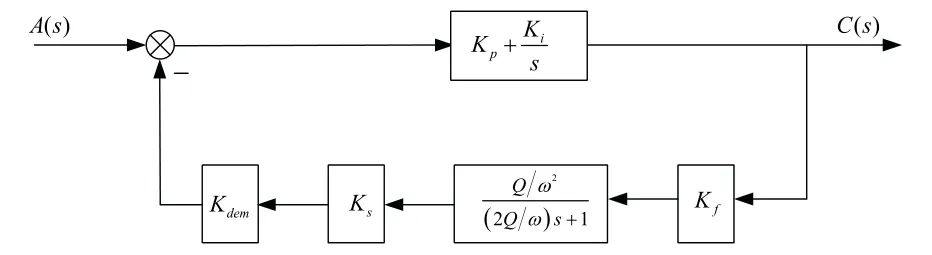
图4 幅度控制回路传递函数方框图Fig.4 Block diagram of amplitude control loop transfer function

综上可得，振动幅度控制回路的闭环传递函数为：

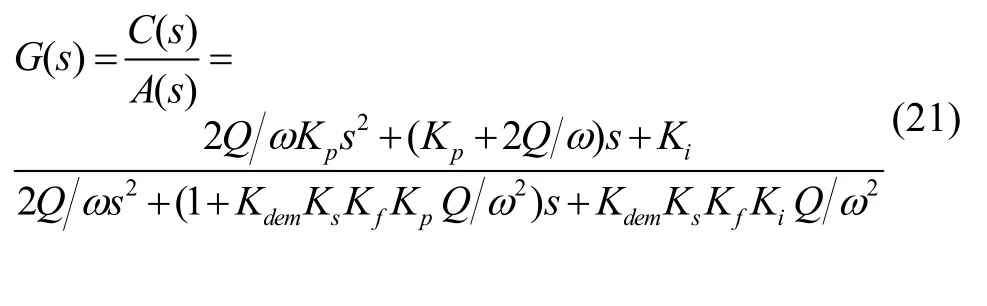
3 振幅控制实现与验证

根据第2 节振动幅度控制回路的设计方案，采用基于AD、DA、FPGA 等数字电子器件的全数字控制方式实现控制回路，控制回路的实现框图和电路如图5所示。

振动幅度控制回路首先从0 °电极检测振动信号，经检测信号处理电路对信号进行滤波和放大处理，再用ADC 进行模数转换送入FPGA。在FPGA 中对采集的数字信号进行数字相敏解调，解算出采集信号的幅值信息，并与幅值设定值求误差，然后误差值经PID控制器调节后，将调节量进行DAC 数模转换，经信号放大电路处理后反馈至180 °电极完成闭环控制。

图5 幅度控制回路实现框图及电路实物图Fig.5 Principle block diagram and circuit diagram of amplitude control loop

以力平衡工作模式为例，进行振幅控制回路性能评估。在力平衡工作模式下，振动幅度控制回路控制陀螺进行恒定幅值振动，设定振幅控制回路的带宽大于10 Hz，采集幅度控制遥测数据如图6所示（约1 h数据）。统计计算幅度控制稳定性优于0.5 ppm，完全满足陀螺性能指标对振幅控制稳定度的要求。

图6 幅度控制值实测曲线Fig.6 Measured Curve of amplitude control value

4 结论

本文针对半球谐振陀螺振动幅度控制问题开展研究，建立了振幅控制回路设计中驱动力与陀螺振动幅度的传递函数，提出了被控对象模型；提出了一种半球谐振陀螺的扫频起振方法；设计了一种半球谐振陀螺振幅控制回路方案，并对振幅控制回路进行数学建模推导，最后采用全数字控制方式实现了振幅控制硬件电路。通过对实验数据进行分析，结果表明本文研究的振幅控制回路的幅值控制稳定性优于0.5 ppm，完全满足陀螺性能指标对振幅控制稳定度的要求。