一种高精度自主式组合导航系统滤波算法
2021-05-27杜学禹王茂松崔加瑞吴文启何晓峰
杜学禹,王茂松,崔加瑞,吴文启,何晓峰
(国防科技大学 智能科学学院,长沙 410073)
捷联惯导系统(Strap-down Inertial Navigation System,SINS)与全球卫星导航系统(Global Navigation Satellite System,GNSS)的组合是车载导航定位系统中最常用的组合方式[1-3],可以提供长时间的高精度输出,满足车辆对实时定位的要求。然而,GNSS 设备的抗干扰能力较差,当处于复杂电磁干扰或信号遮挡环境下时难以提供有效和连续的测量信息,不能满足车辆适应性与自主性的要求。
与GNSS 相比,轮式里程计(Odometer,OD)能自主地测量载车的行驶速度和里程,抗干扰性能较好,与SINS 进行组合有助于提高车载导航系统的自主导航能力和复杂环境下的定位精度[4-6]。但是,传统的SINS/OD 组合导航系统中,高程定位结果在缺乏外源信息约束的情况下,容易随着时间的推移或路程的累积而逐步发散。同时,基于EKF 的惯性基组合导航系统在动态环境下易出现方差估计不一致的问题[7]。
为解决上述问题,本文提出了一种基于状态变换卡尔曼滤波(State Transformation Extended Kalman Filter,ST-EKF)的惯性/里程计/气压高度计组合导航算法。与传统的SINS/OD 组合导航算法相比,该算法首先是采用滤波鲁棒性更好的ST-EKF 替代扩展卡尔曼滤波(Extended Kalman Filter,EKF)。ST-EKF 对系统的速度误差方程进行了更严格的定义[8-12],消除了易受动态环境干扰的比力项,能有效避免方差不一致问题的产生;其次是利用气压高度计(Barometer,Baro)的量测信息对组合导航系统的高程通道进行阻尼。气压高度计利用气压表测量载体周围的大气压力,与测量基准点的表面温度和压力进行对比进而估算载体的高度信息,具有较好的高程测量精度,能有效约束导航系统的高程定位结果,解决传统的自主导航算法高程定位误差易发散的问题。
1 基于ST-EKF 的惯性/里程计/气压高度计系统方程
状态变换卡尔曼滤波(ST-EKF)在文献[8]中首次提出,并被扩展应用在SINS/GNSS、SINS/OD、捷联惯性/多普勒测速仪(SINS/DVL)等组合导航系统中[8-11],实验表明,ST-EKF 在动态环境下比EKF 具有更好的滤波鲁棒性[8-12]。本节推导解释了ST-EKF 框架下的新的速度误差方程,并依此重新定义了系统的状态转移矩阵,建立了基于ST-EKF 的SINS/OD/Baro组合导航系统的误差状态模型[8-12]。
1.1 基于ST-EKF 的速度误差定义
常用的线性速度误差微分方程可以定义为:
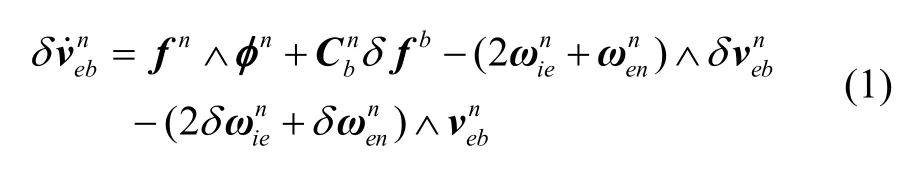
ST-EKF 中将速度误差在同一坐标系下进行了更严格的定义[8-12]:
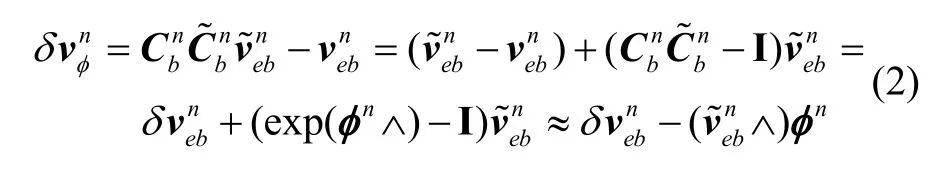
对新的速度误差定义求微分可以得到:

从式(3)中可以看出,ST-EKF 中的速度误差微分方程用重力相关项替代了比力项,而对于一般的车载导航过程来说,几乎为常值,可以有效避免动态环境中比力量化噪声和姿态的剧烈变化带来的计算不精确的问题,提高滤波的鲁棒性。
1.2 基于ST-EKF 的系统误差状态模型
定义SINS/OD/Baro 组合导航系统的21 维误差状态向量x:
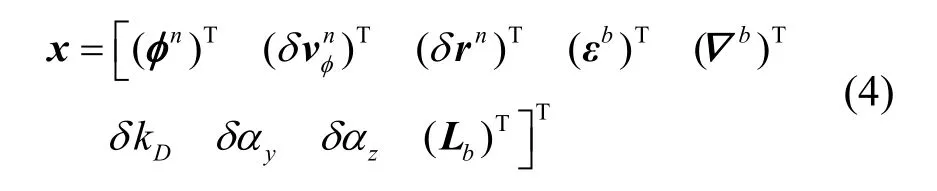
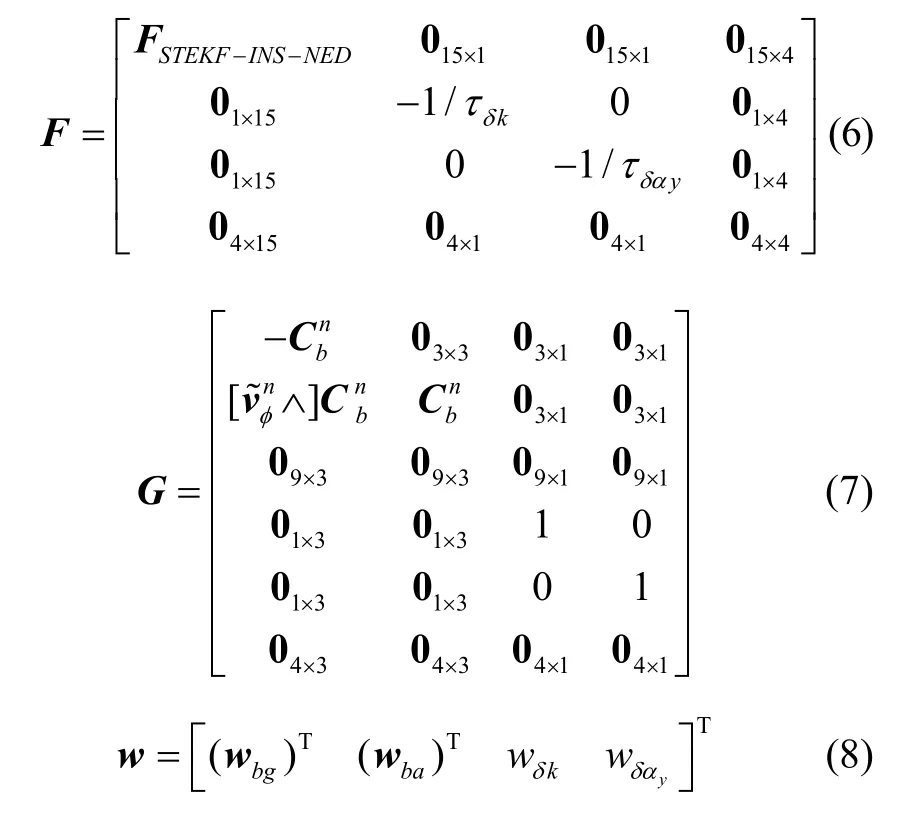
可以构建SINS/OD/Baro 组合导航系统的误差状态方程为:

式中x为误差状态向量,F为系统矩阵,G为噪声转移矩阵,w为过程噪声向量,它们具体定义如下[8-12]:
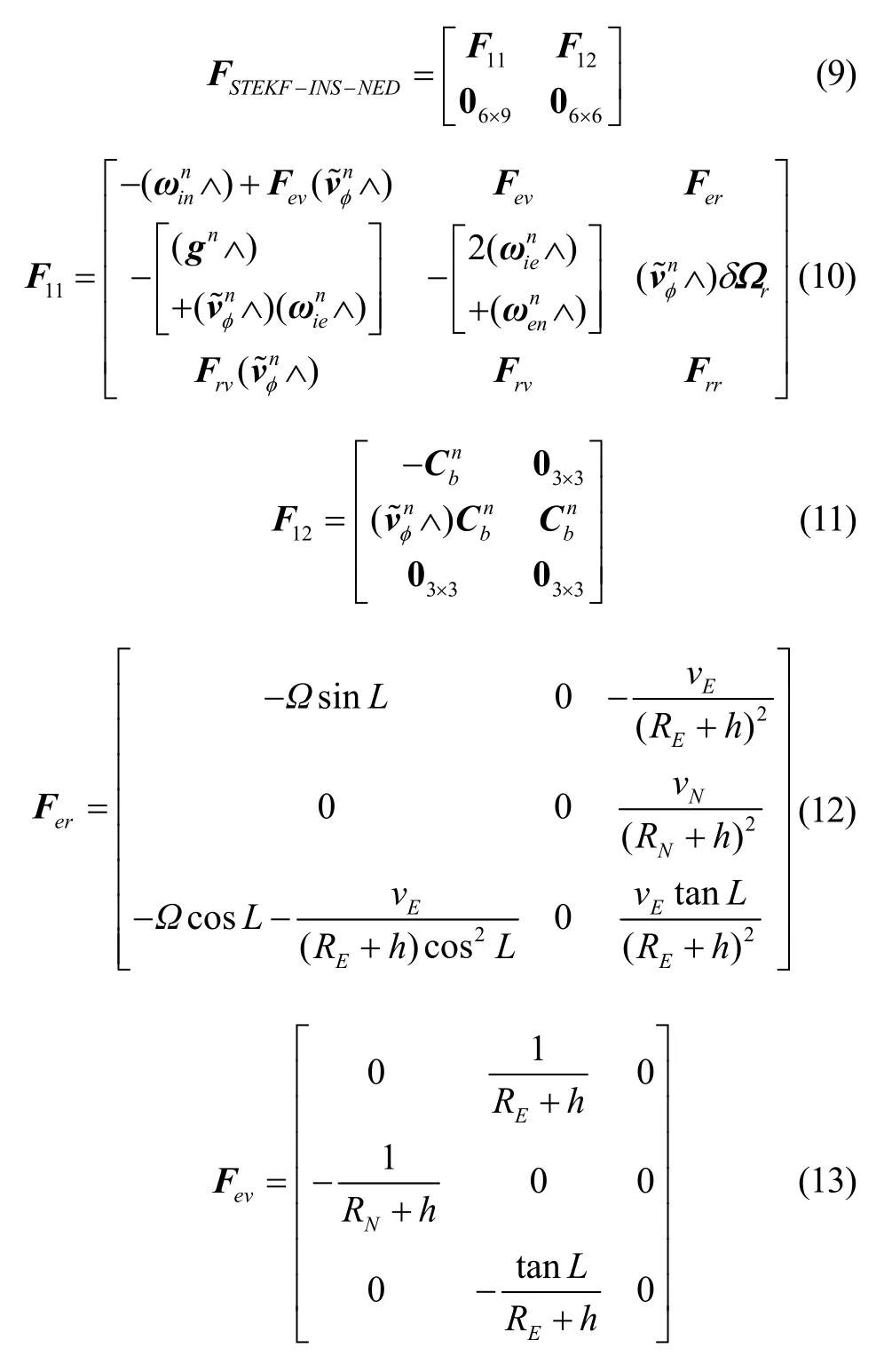

2 基于ST-EKF 的惯性/里程计/气压高度计组合导航量测方程
为设计出能够精确快速地定位定向,并具有良好的自主性、适应性和可靠性的车载导航系统,本文引入轮式里程计与气压高度计作为辅助导航设备,利用二者提供的量测信息,限制惯性导航系统中误差的累积,从而改进导航性能。本文设计的组合导航系统的结构原理如图1所示:
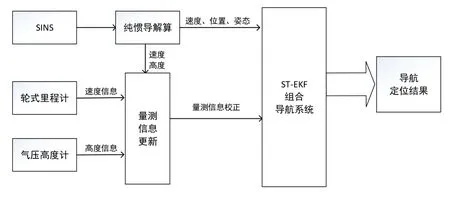
图1 组合导航系统原理图Fig.1 Schematic diagram of integrated navigation system
假设IMU 系b 与车体系m 之间的安装角是小角度,则方向余弦矩阵可以写为:
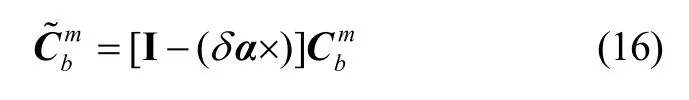
其中,αδ是捷联惯导系统与车体之间的安装误差。
由捷联惯导系统解算的速度在m 系下的投影可以表达为:
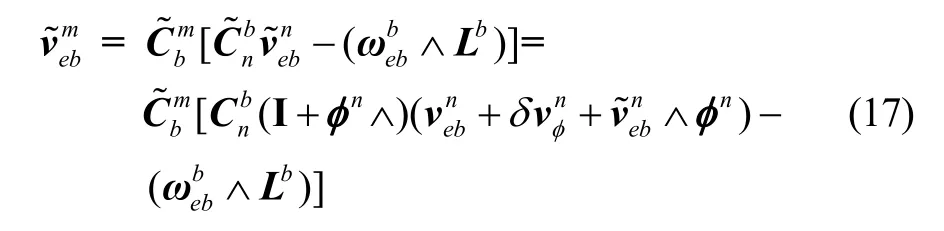
将SINS 解算出的速度信息投影到里程计坐标系下与里程计的速度相减作为系统的速度观测量,即:
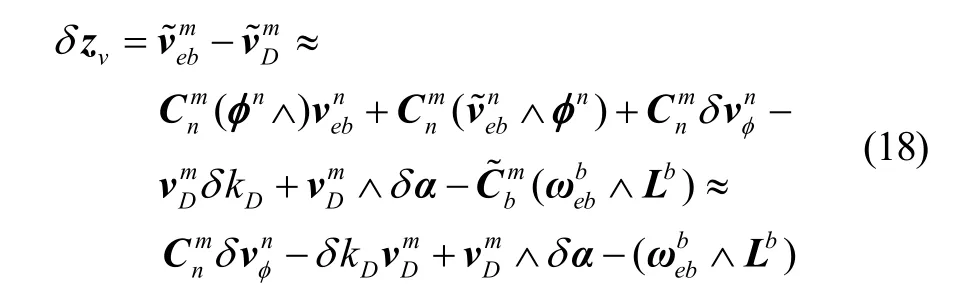
在标准大气模型下,气压高度计测量公式如下[13]:
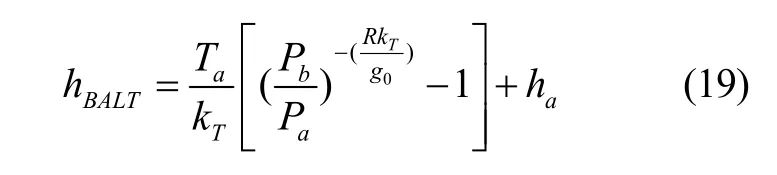
在实验过程中,气压高度计采集当地实时气压值和温度值数据,以及基准点的气压值和温度值,由公式(19)可得气压高度,将惯导解算得到的高程信息与该量测高度相减,作为SINS/OD/Baro 组合导航系统的高程观测量,即:
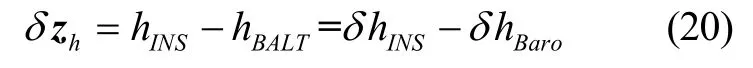
结合式(18)与式(20),可以得到基于ST-EKF 的SINS/OD/Baro 组合导航系统的观测量:
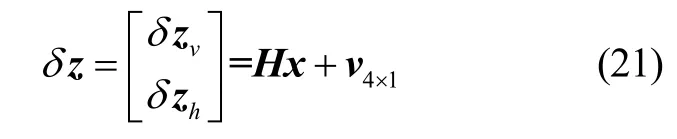

由于基于ST-EKF 的SINS/OD 组合导航系统滤波估计的是新的速度误差状态,所以滤波后速度状态的更新公式应为[8-11]:
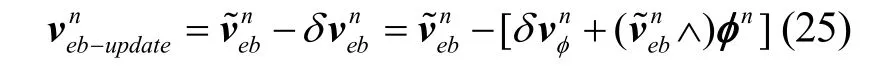
因为ST-EKF 中姿态失准角和位置误差状态的定义未作改变,所以姿态和位置的校正与传统的EKF 一致。
3 实验结果与分析
3.1 实验设计
为了检验本文提出的基于 ST-EKF 的SINS/OD/Baro 组合导航算法的应用效果,对真实的长行驶里程车载实验数据进行事后处理,并与同等实验条件下基于EKF 的SINS/OD 组合导航算法、基于ST-EKF 的SINS/OD 组合导航算法的水平定位精度、高程解算结果作出了对比。
为了使事后处理结果更具有参考价值,本次实验分别采用了两组不同行驶条件下的实验数据,其中一组来自于一次沿长沙市环城高速的车载实验,行车时间约为3.7 h,行驶里程总计154 km,在百度卫星地图下的行车轨迹如图2所示;另一组来自于一次长沙市至岳阳市的长里程行驶车载实验,行车时间约为4.2 h,行驶里程总计235 km,在百度卫星地图下的行车轨迹如图3所示。

图2 二维车辆行驶轨迹图(第一组)Fig.2 Two dimensional trajectory of the land vehicle experiment(Group 1)
图3 二维车辆行驶轨迹图(第二组)Fig.3 Two dimensional trajectory of the land vehicle experiment(Group 2)
实验车辆配备了导航级的高精度光纤陀螺IMU、标度因数约为898 p/m 的轮式里程计和MS5611 型气压传感器,三种传感器进行组合导航的滤波频率为1 Hz。实验车辆的传感器配置和工作模式如图4所示。
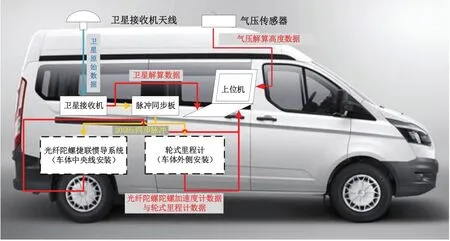
图4 车载实验传感器配置及工作模式Fig.4 Sensor configurations and working mode of the land vehicle field test.
其中,IMU 的输出频率为200 Hz,陀螺零偏稳定性为0.002 ° /h,角度随机游走为;加速度计零偏稳定性为50 μg,速度随机游走为。在跑车实验中,车辆静止180 s 进行初始对准。
组合导航过程中采用的气压高度测量值由MS5611 型气压传感器提供的气压、温度数据解算得到,两组实验中该测量值与基准高度的对比分别如图5、图6所示。
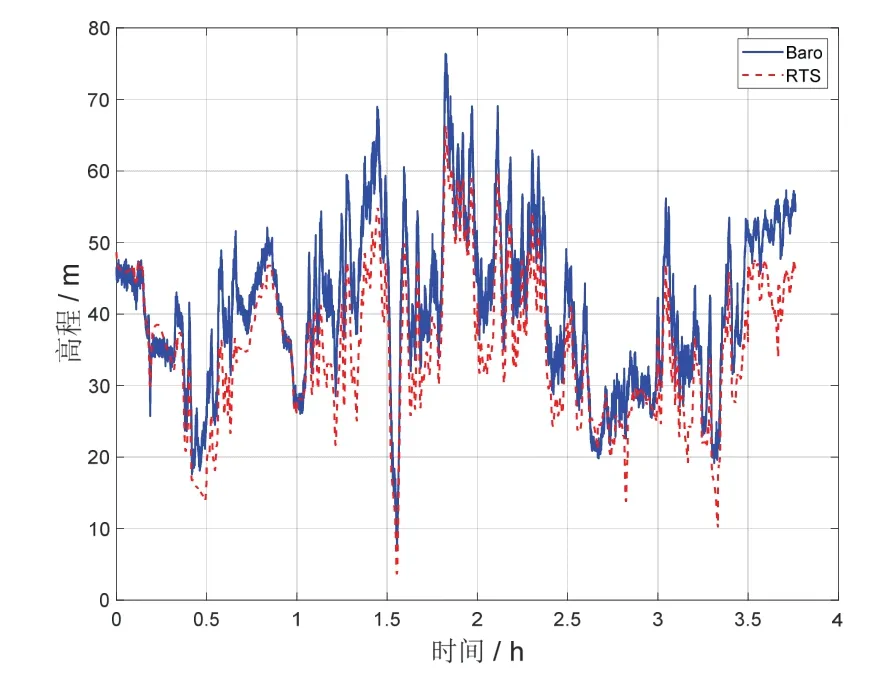
图5 气压高度计输出高度与基准高度对比(第一组)Fig.5 Comparison of barometric altimeter output height and reference height(Group 1)
本节中采用的基准位置由惯性/差分卫星组合导航事后平滑算法[12]解算得到,数据用RTS 表示。精度在1 m 以内。
由图5、图6 可以看出,在不同的行驶环境下,气压高度计呈现出不同的测量精度,这也将影响组合后导航系统的定位精度。本章将分别针对两组实验数据的解算结果,论证该算法在不同行驶环境下的应用效果以及相对传统组合导航算法的改进效果。
3.2 长沙市环城高速车载实验
图7 为第一组实验中,三种组合导航算法解算得到的水平定位结果,分别相对于基准位置的定位误差和精度随时间以及行驶里程变化而产生的变化趋势。
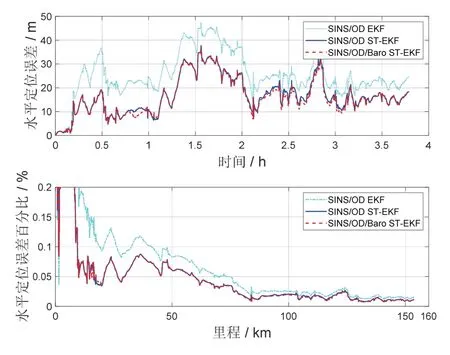
图7 水平定位结果对比(第一组)Fig.7 Comparison of horizontal positioning results(Group 1)
图8 为第一组实验中,三种组合导航算法解算得到的高程以及基准高度随时间的变化曲线。
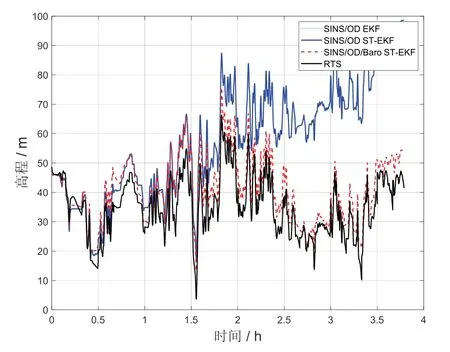
图8 高程定位结果对比(第一组)Fig.8 Comparison of height positioning results(Group 1)
观察图7、图8 可以发现,采用ST-EKF 替换传统的EKF 框架后,SINS/OD 组合导航算法的水平和高程定位精度均得到提高。而在引入气压高度计的量测信息后,基于ST-EKF 的SINS/OD/Baro 组合导航算法在保持较高的水平定位精度的同时,高程定位精度也获得了大幅度提升。
为了更客观地对比评价三种组合导航算法的导航定位精度,对三种算法的解算结果作出了量化统计,其中,表1 统计了第一组实验中三种算法全程水平定位结果的均方根误差(RMSE)以及RMSE 占总行驶里程的百分比,表2 则统计了第一组实验中三种算法全程高程定位结果的RMSE。
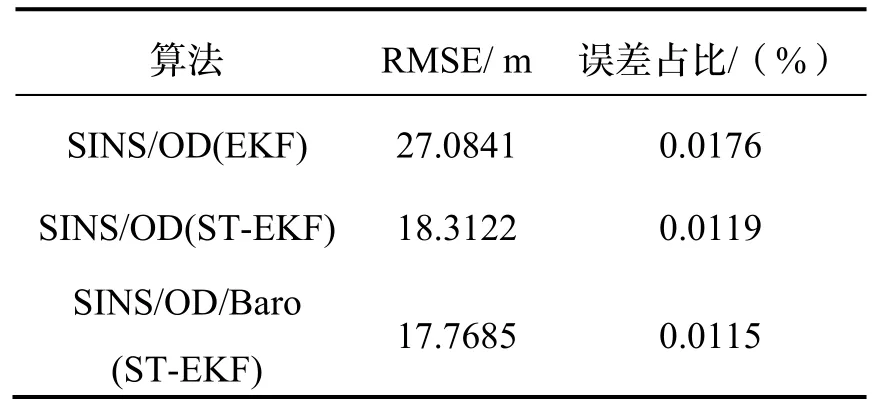
表1 水平定位误差统计表(第一组)Tab.1 Statistical table of horizontal positioning error(Group 1)
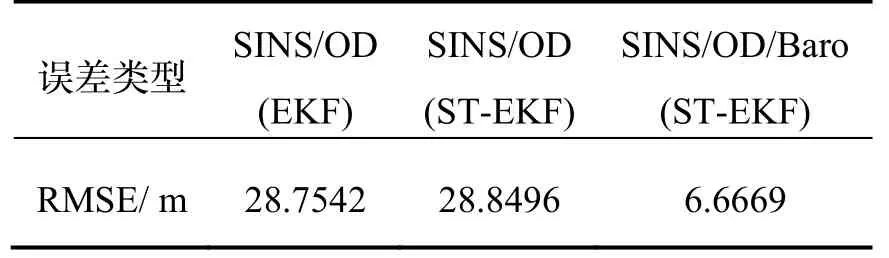
表2 高程误差统计表(第一组)Tab.2 Statistical table of height error(Group 1)
观察表1、表2 可以发现,第一组实验中基于EKF的SINS/OD 组合导航算法全程的水平定位结果的RMSE 为 27.0841 m,高程定位结果的 RMSE 为28.7542 m。而基于ST-EKF 的SINS/OD/Baro 组合导航算法全程的水平定位结果的RMSE 为17.7685 m,高程定位结果的RMSE 为6.6669 m,两种RMSE 分别减少了34.40%和76.81%。
结合第一组实验的实验结果可以发现,在环城高速的行驶过程中,气候条件变化较小,气压高度计具有较好的测量精度,其测量结果引入本文提出的高精度组合导航算法,对导航系统的高程通道起到了较好的阻尼效果,有效地抑制高程定位误差的发散趋势,提高了系统的导航定位精度。
3.3 长沙市至岳阳市直线行驶车载实验
与第一组实验不同,第二组是一组跨地市的长里程直线行驶车载实验,行驶环境更加复杂,气候条件变化较大,气压高度计产生了较高的测量误差,对导航算法的解算精度提出了更高的要求。
与图7、图8 相对应,图9、图10 分别为第二组实验中三种组合导航算法的水平定位结果、高程定位结果对比图。
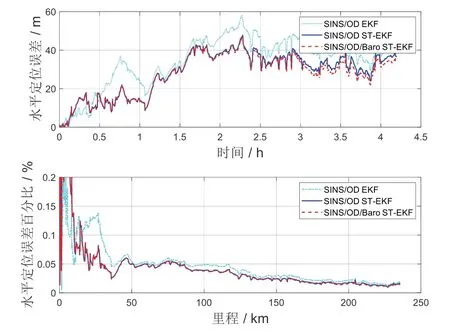
图9 水平定位结果对比(第二组)Fig.9 Comparison of horizontal positioning results(Group 2)
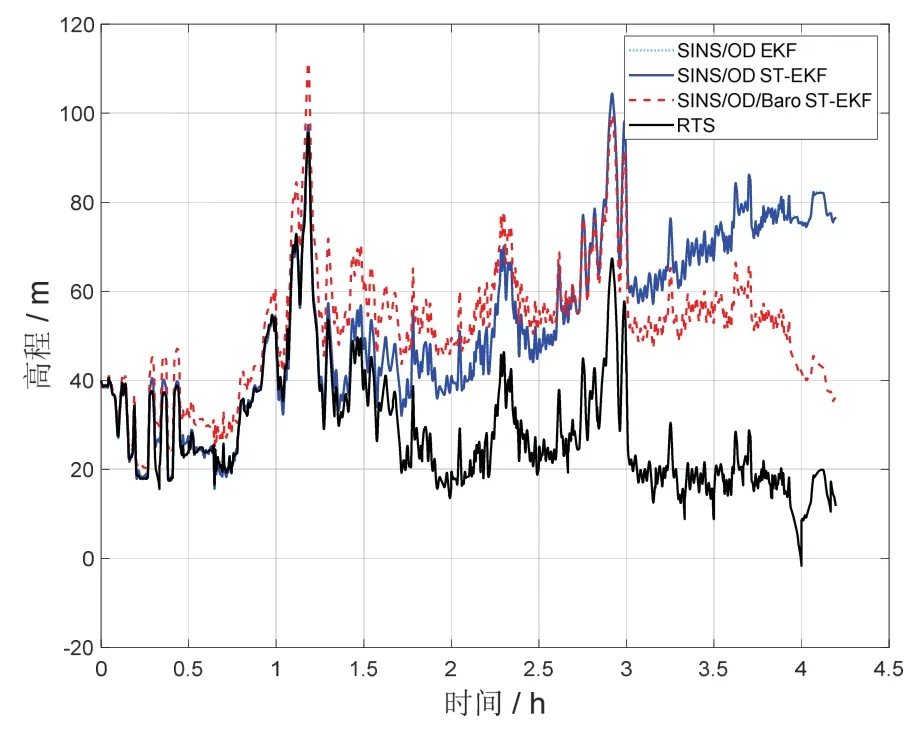
图10 高程定位结果对比(第二组)Fig.10 Comparison of height positioning results(Group 2)
表3、表4 则分别量化统计了第二组实验中三种算法全程的水平定位误差和高程定位误差。
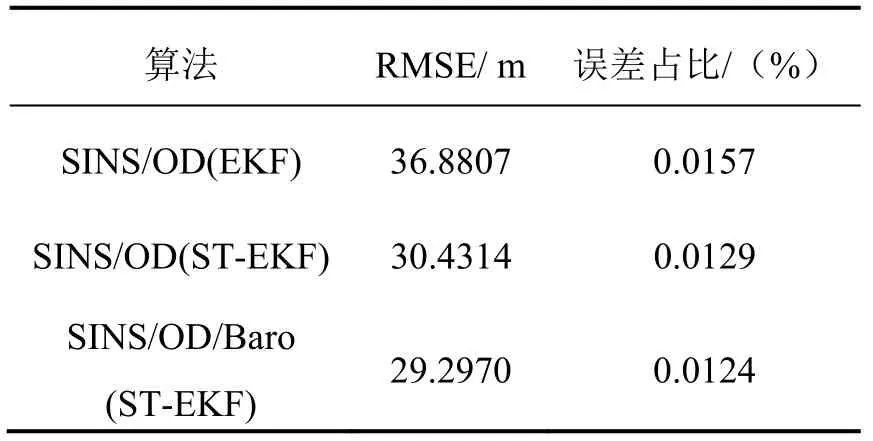
表3 水平定位误差统计表(第二组)Tab.3 Statistical table of horizontal positioning error(Group 2)

表4 高程误差统计表(第二组)Tab.4 Statistical table of height error(Group 2)
结合图9-10,表3-4 可以发现,在跨地市的长里程行驶环境中,本文提出的高精度组合导航算法的水平定位精度依然相对传统的导航算法提高了21%,并且在气压高度量测数据不太理想的情况下,减缓了系统高程定位误差发散的趋势,进一步证明了该算法在不同行驶环境下的普适性。
4 结论
针对卫星拒止的条件下,长行驶里程任务中的导航定位精度问题,本文提出了一种基于ST-EKF 的SINS/OD/Baro 高精度车载自主导航滤波算法。实测车载实验数据的事后处理表明,该算法在不同的行驶环境中均能保持较高的导航定位精度,全程的水平定位精度优于0.05%D。同时,该算法能有效利用气压高度计的量测值对导航系统的高程通道进行阻尼,改善了传统的基于EKF 的SINS/OD 组合导航系统高程定位误差易发散的问题。因此,该算法可以帮助车辆在缺乏卫星信号校正的复杂环境下,迅速确定自身所处区域,使得视觉等传感器的后续处理能更加精确,具有良好的工程应用价值。
