基于因子克里金分析方法的航空重力梯度降噪
2021-05-27赵德军孙中苗赵东明
赵德军,孙中苗,赵东明
(1.信息工程大学地理空间信息学院,郑州 450001;2.西安测绘总站,西安 710054;3.地理信息工程国家重点实验室,西安 710054;4.西安测绘研究所,西安 710054)
相对于航空标量重力测量和矢量重力测量而言,航空重力梯度测量有两大显著优势[1-3]:1)最大的优势在于其不受载体运动和厄特弗斯效应的影响;2)重力梯度以重力场的曲率描述重力场区域结构,包含地球物理学和大地测量中急需的局部重力场几何信息(水准面的平均曲率、铅垂线的曲率等),因而重力梯度测量更能反映重力场的精细结构,敏感重力场的短波变化。
航空重力梯度测量能获取高分辨率和高频谱的重力梯度信号,能更好地描述小的异常特征。因此,在航空重力梯度数据处理时,既要去除高频噪声,又要保留高频的有效重力梯度信号,是一个巨大的挑战。在生产作业中,像巴特沃斯这样的经典低通数字滤波器仍被广泛采用,滤波器的截止波长一般根据数据的采样率和已知地质构造的特征信息来估计,并需要经过多次试验得到。低通滤波器存在选择最优参数的难题,以及方法本身无法针对具体数据进行参数自适应选择的问题[1-3]。
克里金插值是地球物理统计学中常用的空间数据插值估计方法,可以客观地估计数据的噪声水平和平滑度。在地球物理中,观测到的信号既可以看成是区域分量与局部分量的叠加,又可看成是深部地质体与浅层地质体所引起的异常的综合反映,同时还含有不可忽略的系统误差。因子克里金法允许将区域化变量分解成多个不同尺度的分量(即因子),每个因子都有其对应的变异函数,每个因子的变程代表地质体的平均直径大小。
因子克里金法具有多尺度分析等诸多功能和优点,因而广泛应用于地球物理与地球化学勘探[4],图像处理与分析[5,6],水土环境监测[7,8]等领域。但在重力梯度降噪方面未见相关报道,因此本文首次将其应用于航空重力梯度数据降噪处理,取得了显著的效果。模拟试验表明,相对于传统的低通滤波器,重力梯度各分量精度平均提升了36%,垂直梯度分量尤为显著,精度提升了42%。
1 因子克里金降噪法
1.1 变异函数
克里金理论,就是用变异函数来描述区域化变量以解决有关地学问题的理论,其核心是变异函数。区域化变量的结构分析,就是通过区域化变量有限的空间观测值来构建相应的理论变异函数模型,以表征该变量的主要结构特征。
设()Z x是区域化变量,有了二阶平稳假设或本征假设,就可以给出变异函数的计算公式[5]:
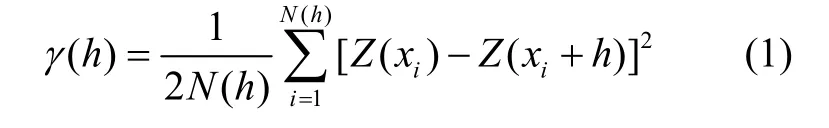
1.2 因子克里金
因子克里金将区域化变量分解成多个尺度的因子,而每个因子都对应一个变异函数。因子克里金滤波的思路:从实验变异函数中,将各因子对应的变异函数提取出来,认为小尺度变异函数对应的因子是需要滤掉的噪声,保留大尺度的变异函数对应的因子作为有效信号,从而实现滤波的过程。区域化变量可以认为是不同地质体相互作用的叠加,因此将区域化变量分解为[5]:
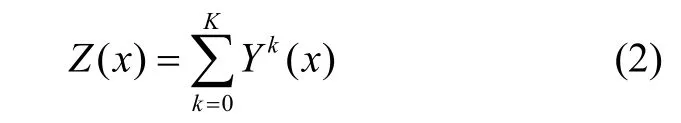
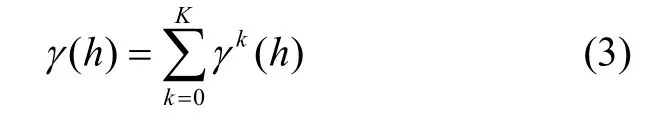
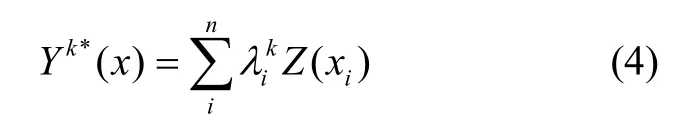
根据估计方差最小原则,对每个因子()k Y x导出克里金方程组[5-7]:
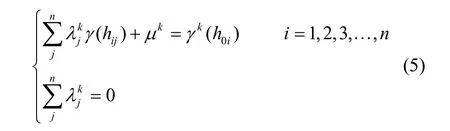
从因子克里金方程组可看出,因子克里金除了需要知道原始数据的变异函数()hγ,还要知道每个因子的变异函数。利用分解后各因子的变异函数按式(5)解出权系数,然后用式(4)就可得到对原空间数据各个因子的估计值。
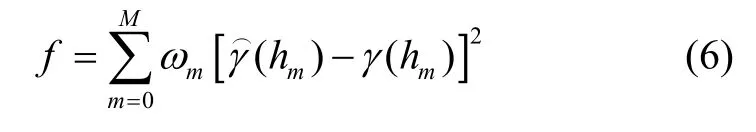

理论变异函数通常是非线性模型,因此在采用加权最小二乘拟合之前,需要将非线性模型转换为线性模型。一般采用泰勒级数将非线性模型转换为线性模型,也可以采用多项式逼近的方法将其转换成线性模型。另外,除了从数学上将非线性模型线性化外,还可以利用一些数学软件里的遗传算法、模拟退火法等最优方法来解决非线性回归问题[9]。
2 模拟数据分析
对于模拟实验,可以采用噪声衰减因子β来估计噪声衰减量。用X表示模型的真实梯度值,Xn表示增加噪声后的梯度值,Xr为经过滤波处理后的梯度值:
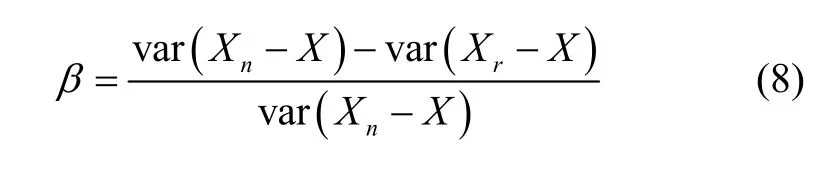
式中var 表示计算的方差。当β为正时,说明噪声被滤除,β的大小表示去除噪声的能力,当β趋于1,表示Xr中几乎不含噪声成分。
利用下面的均方根误差来表示滤波后数据的精度:
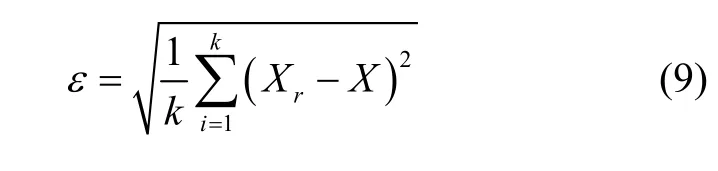
模拟一个地质特征显著的重力梯度场,假定在平面坐标系中,分布8 个已知梯度的样本点,其坐标和值如表1所示。采用套合变异函数模型,用普通克里金插值,内插坐标网格的梯度值。网格的x和y坐标范围均从0 m 到100 m,坐标间隔1 m。为了使模拟的模型更有说服力,变异函数采用1 个指数模型和1个球状模型的套合结构。指数模型的基台值为20 E2,变程10 m,球状模型的基台值为4 E2,变程为60 m。模拟的模型梯度如图1(a),然后在模型梯度值的基础上,添加方差为10 E2的高斯白噪声,如图1(b)。
根据图1(b)统计出实验变异函数,然后采用1 个块金模型,2 个球状模型的套合变异函数来逼近实验变异函数,并提取出各因子的理论变异函数,其参数见表2。是块金值的变异函数,通常认为块金值表示随机噪声,这里块金值为8.24 E2,与假设的噪声方差10 E2比较吻合。的变程较小,认为是局部分量的变异函数,代表小尺度的地质体;的变程较大,一般认为是区域分量的变异函数,代表大尺度的地质体。这样就将图1(b)分解成3 个不同尺度的分量。图1(c)、图1(d)和图1(e)分别是对应的大尺度区域分量,对应的小尺度局部分量,以及对应的随机噪声分量。
将大尺度分量和小尺度分量叠加,认为是有效信号,如图1(f)。对比图1(f)和图1(a),可看出采用因子克里金滤波后的图像仍然有部分噪声残留。同时,采用空域高斯滤波低通对图1(b)降噪,高斯滤波器的方差设为10 E2,滤波后的梯度为图1(g)。
表3 是不同方法滤波后的衰减因子和误差表。对比图1 和表3,可看出,高斯滤波虽然图像比较平滑,但是其衰减因子比较低,只有0.76,误差为1.56 E。因子克里金滤波后的图像不太平滑,但衰减因子达到了0.93,误差为0.91 E。所以可以说,空域高斯滤波过度平滑,滤除噪声的同时,还滤除了部分有用信号,而因子克里金滤除高频噪声的同时,还保留了高频信号。
同时还采用普通克里金滤波对图1(b)进行降噪处理,滤波后的图像接近图1(f)。从表3 看出普通克里金滤波的衰减因子为0.90,误差为0.97 E,滤波效果略低于因子克里金。

表1 模拟样本点的坐标和梯度值Tab.1 Coordinates and gradient values of simulated points
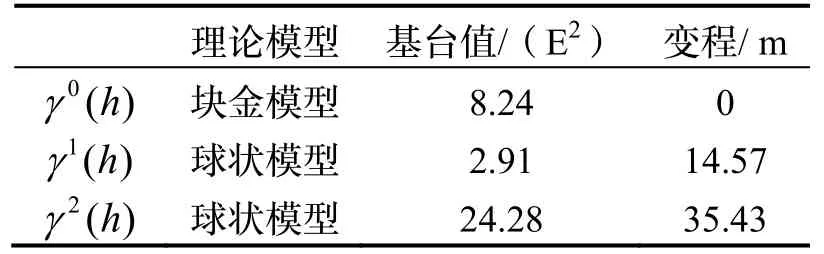
表2 拟合的套合变异函数的参数Tab.2 Parameters of fitted nested variogram
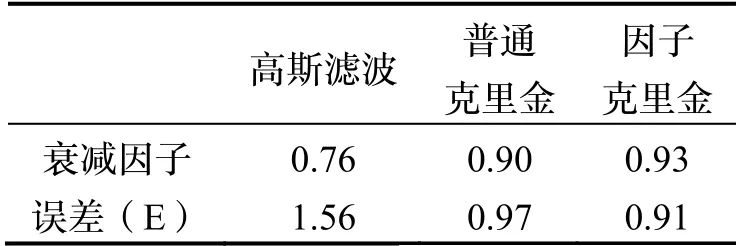
表3 噪声衰减因子和误差比较Tab.3 Noise attenuation factor and error comparison
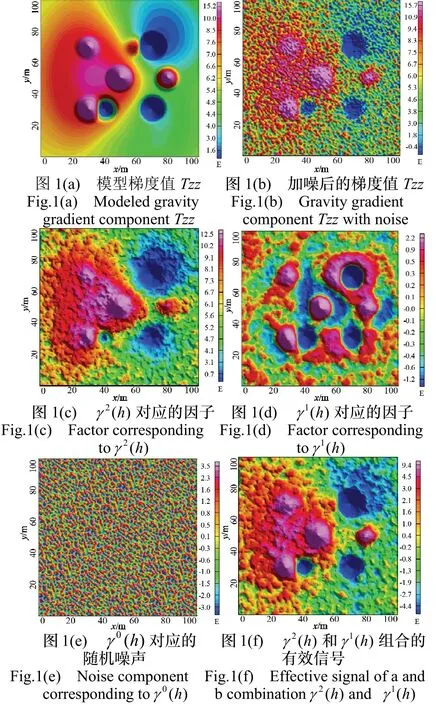
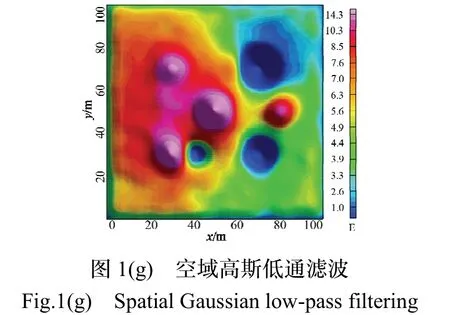
图1 因子克里金分析图Fig.1 Factor Kriging Analysis diagram
本文还统计了滤波前后信号的径向平均功率谱密度(图2),从中看出因子克里金降低了高频段的噪声能量,但还残留了部分噪声,保留了梯度的真实成分。而高斯滤波降低高频段的噪声的同时,又滤掉了部分有用信号,过度平滑了信号。
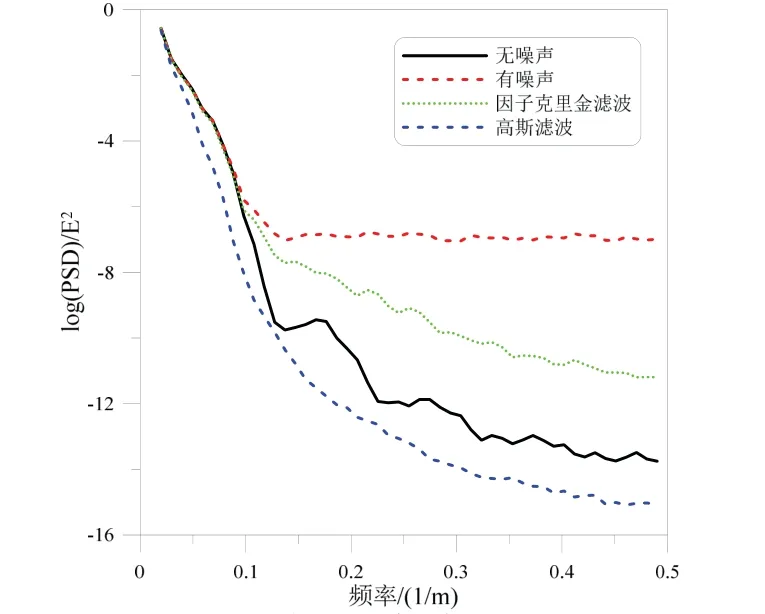
图2 滤波前后功率谱曲线对比图Fig.2 Comparison of power spectrum curves before and after filtering
为了充分说明因子克里金的降噪效果,本文还对重力梯度的其它5 个分量进行了模拟实验。图3 中从上到下分别是Txx、Txy、Txz、Tyy 和Tyz 共5 个分量的降噪效果图。其中,图3 第1 列为模拟的无噪声梯度分量值,其参数与图1(a)中垂直梯度分量Tzz 相同。第2 列为在第1 列模型梯度值的基础上,添加方差为10 E2高斯白噪声后的梯度分量。第3 列为采用因子克里金降噪后的梯度分量图,从中看出对于不同的梯度分量,因子克里金都能有效地降低噪声的干扰。

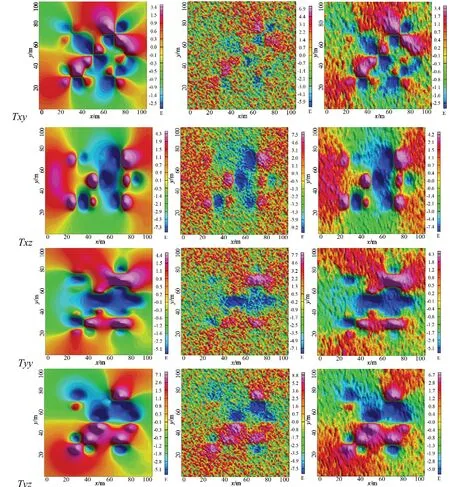
图3 重力梯度分量降噪图Fig.3 Noise reduction of gravity gradient component
表4 为根据式(9)统计的重力梯度分量降噪误差表,可以看出普通克里金方法和因子克里金方法都能有效地降低重力梯度分量的噪声,且因子克里金法略优于普通克里金降噪法。因子克里金法相对于高斯空间滤波,各梯度分量精度均提升30%以上,平均精度提升了36%,尤其是垂直梯度分量精度提升了42%。
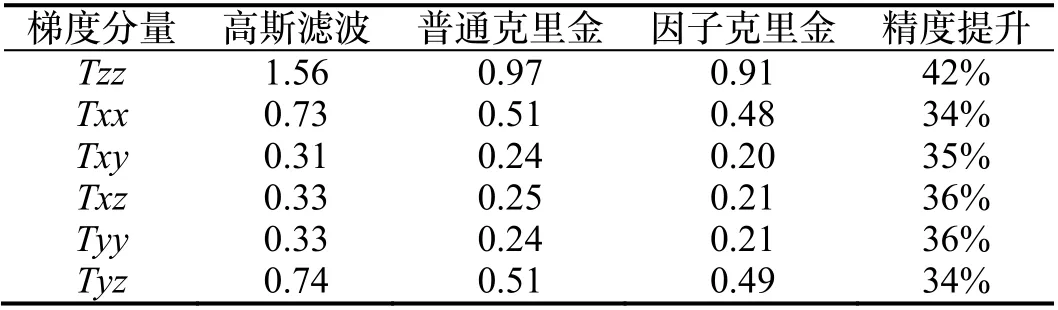
表4 重力梯度分量降噪误差统计(单位:E)Tab.4 Error statistics for noise reduction of gravity gradient component(unit:E)
3 实测数据分析与降噪处理
数据来源于贝尔地理空间公司在加拿大圣乔治湾测量的重力垂直梯度Tzz。沿飞行测线数据的采样间隔约为80 m,主测线间距为500 m,副测线距为5000 m,贴地起伏飞行高度为100 m。选取垂直梯度做实验,区域选取地质结构明显的区域,范围为纬度48 °11 ′~48 °25 ′,经度-59 °14 ′~-58 °54 ′,区域内共24121 个测点。
3.1 空间变异分析
将测线数据按照通用横轴墨卡托投影,转换成平面直角坐标 。设置滞后距分段为500 m,最大搜索半径设置为区域对角线长度的一半,约15000 m,角度容差为22.5 °,分别计算了重力梯度在方位角为0 °,45 °,90 °,135 °四个方向上的实验变异函数,并绘制出拟合后的球状模型变异函数(图4),其参数见表5。从图4 和表5 中看出,45 °和90 °方向的实验变异函数较为理想,变异值在滞后距约10000 m 处趋于稳定。而0 °和135 °方向的变异结构较差,当滞后距大于变程后,实验变异值并未像理论值一样趋于稳定,与理论变异函数偏差较大,拟合误差分别达到5732 E2和3682 E2。
从图4 的拟合曲线和表5 的拟合参数可知,此处的垂直梯度存在明显的各向异性。各向异性是由于特定的地质体构造引起的,按其性质可分为几何各向异性和带状各向异性。几何各向异性指的是变异函数在不同方向上具有相同的基台值、不同的变程,即在相同距离上不同方向的两点间平均变异程度不同。
从表5 中可看出,此处的垂直梯度明显属于几何各向异性。二维各向异性的变程图是以东西方向(方位角90 °)为主轴(变程9923 m),南北方向(方位角0 °)为次轴(变程4812 m)的椭圆。对于几何各向异性的变异函数,可通过坐标旋转变换和构建伸缩矩阵将各向异性结构变换成各向同性结构,也即将椭圆形状的变程图转换成圆形的变程图。对于本区域,旋转角度为0 °,各向异性比例系数K=9923/4812,因此只需要将原始数据的y坐标(指向北向)乘以比例系数K,得到新的坐标系。在新坐标系下,垂直梯度具有各向同性的空间结构。
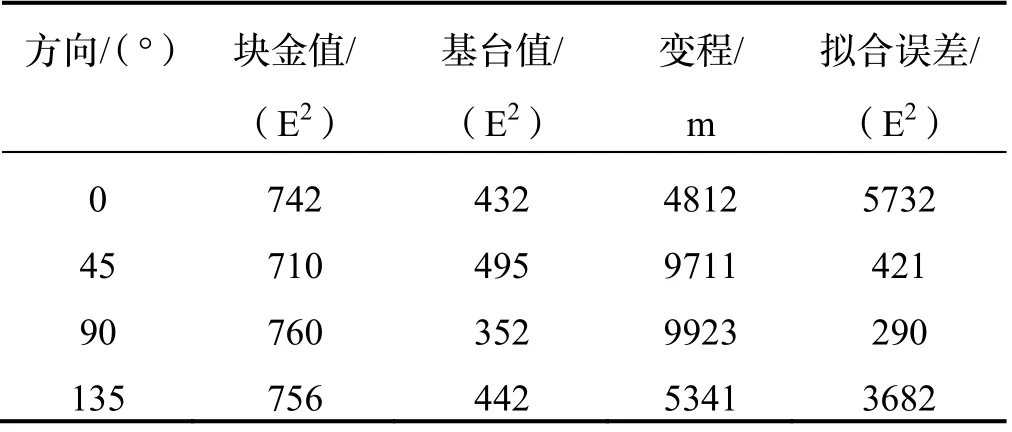
表5 不同方向拟合的球状变异函数参数Tab.5 Spherical variogram parameters fitted in different directions
对经过坐标旋转和伸缩变换后的垂直梯度,重新统计各向同性的实验变异函数,如图5。从图5 中看出,各向同性的空间实验变异结构明显好于各向异性的空间结构,滞后距大于变程后,实验变异值逐渐趋于平稳,与理论变异函数相符。拟合球状模型块金值为720 E2,基台值438 E2,变程10190 m,拟合误差的均方差为18.3 E2。
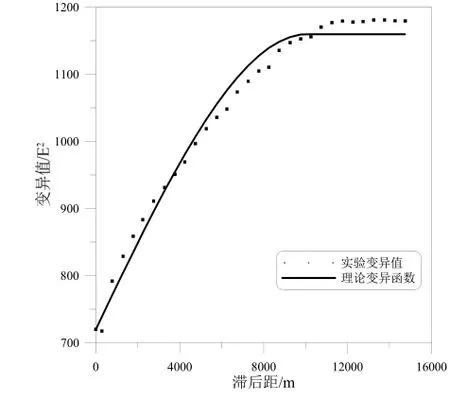
图5 各向同性变异图Fig.5 Isotropic Variogram
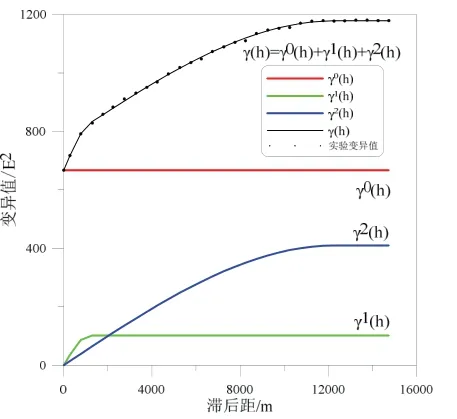
图6 套合变异函数图Fig.6 Variogram of nested fitting
3.2 降噪处理
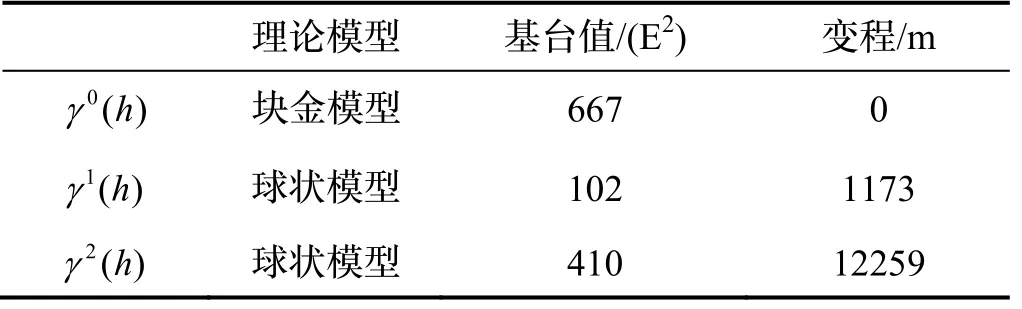
表6 理论变异函数模型参数Tab.6 Theoretical variogram model parameters
用分解出来的变异函数,计算不同尺度的因子,插值间隔为250 m,然后将y坐标(指向北向)除以各向异性比例系数K,恢复成旧坐标系,见图7,坐标单位是km。
图7(a)是原始垂向重力梯度值,由于数据中含有大量噪声,因此掩盖了有效信息。通过因子克里金将原始梯度信息分解成3 个尺度的因子:图7(b)是对应的高频率因子,认为它是随机噪声;图7(c)是对应的小尺度因子;图7(d)是对应的大尺度因子,从图中看出,随机噪声能够有效地被压制,呈现出明显的地质特征,且地质特征的走向信息也有很清晰的反映。
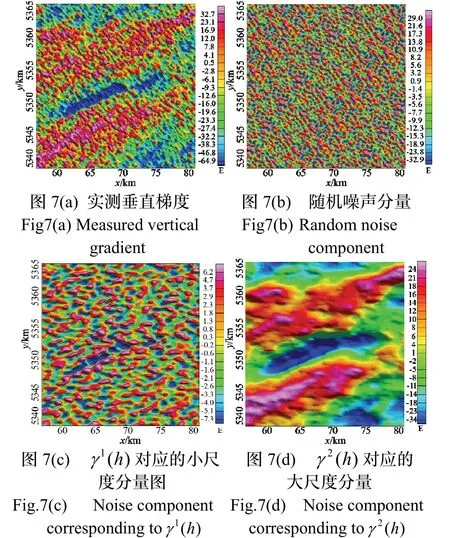
图7 垂直重力梯度的因子克里金滤波Fig.7 Factor Kriging filtering of vertical gravity gradient
4 结论
因子克里金分析的关键是分解各因子的变异函数,获取了各因子的变异函数后,就可以通过因子克里金方程组,将区域变量分解成不同尺度的分量。继而将重力梯度分解成随机噪声、小尺度分量和大尺度分量,以此实现降噪的目的。从模拟和实测数据的实验可看出:
(1)因子克里金滤波可以自动获得各项滤波参数。因子克里金分析法通过对采样数据的统计分析来构建空间变异函数,从而获取块金值,基台值、变程等滤波参数。该过程是完全基于数据驱动的,不需要任何先验信息,而传统的空间滤波器的参数需要根据经验确定;
(2)因子克里金滤波直接采用离散点数据。传统的空间滤波方法往往需要规则网格,而因子克里金滤波是基于离散点的滤波,不需要事先将离散点数据网格化;
(3)模拟实验表明,因子克里金降噪法相对于传统的空间滤波精度有显著的提高,重力梯度各分量精度均提升30%以上,尤其是垂直梯度分量精度提升了42%,说明因子克里金降噪法适用于地质特征明显区域的梯度场降噪;
(4)通过实测航空重力梯度的空间变异分析发现,该地区的变异函数呈现出较强的各向异性,因此需要将各向异性的重力梯度转换为各向同性的重力梯度才能采用因子克里金降噪,经降噪后该地区的重力梯度呈现出明显的地质特征。
致谢:感谢加拿大自然资源部(Natural Resources Canada)提供的圣乔治湾实测航空重力梯度数据,允许使用此数据进行研究并发表研究成果。
