不同应变率下煤岩破坏特征及其本构模型*

郑 钰，施浩然,2，刘晓辉,2，张文举

（1. 西华大学能源与动力工程学院，四川 成都 610039；2. 西华大学流体与动力机械教育部重点实验室，四川 成都 610039；3. 中国市政工程西南设计研究总院有限公司，四川 成都 610084）

随着国家经济高速发展，煤炭资源作为我国最重要的基础性能源，其需求量日益增长，如何安全、高效开采发人深思。众所周知，煤炭开采是原岩应力产生扰动，原有应力平衡被打破，进而发生应力转移、重分布的平衡调整过程[1]，该过程煤岩的动态力学特性、变形破坏特征不仅呈现出显著的应变率效应，而且其破坏过程导致的冲击地压、瓦斯突出等更是典型的动力灾害。因此，研究动态应变率下煤岩的变形破坏特征及其本构关系能够为安全、高效进行煤矿开采提供强有力的科学依据。

目前，许多学者通过霍普金森压杆试验[2-5]、数值模拟[6]等方法对冲击荷载作用下煤岩的力学特性及破坏特征展开了研究，发现煤岩的强度、变形特征参数具有明显的应变率相关性，煤岩的变形破坏形态随应变率变化差异显著，且不同煤岩或相同煤岩不同外界条件破坏形态各异。煤岩开采过程中常常伴随岩体破碎和碎块块度分布等问题，谢和平等[7]、高峰等[8]从煤岩宏观破坏后块度分布所具有的统计自相似性出发，提出了从分形几何角度对煤岩碎块块度分布进行统计分析，指出分形维数是反映岩石破碎程度恰当的统计特征量。张文清等[9]、丁鑫等[10]、Zhao 等[11]同样利用霍普金森压杆对煤岩试样展开了不同应变率下的冲击压缩试验，再次指出试验后煤岩碎块具有明显的分形特性，但不同煤岩由于其自身较强的离散性特征，破碎块度分布存在着较大的差异。

除此而外，有关岩石动态本构关系的研究也受到广泛关注，目前使用较多的岩石本构模型主要分为元件型和强度型两种。元件型模型历史悠久，最早可追溯到1974 年Lindholm 等[12]提出的硬岩过应力模型，为研究岩石应力、应变、应变率的关系提出了一种新的方向。元件型模型能较好描述岩石的力学特征[13-15]，但此类模型拟合参数多、求解复杂且拟合参数的规律性受试验影响大[16-18]，为克服这一不足，强度型模型的构建应运而生。基于岩石微元体的强度服从Weibull 统计分布的假设，朱晶晶等[19]建立了能较好反映花岗岩强度、应变与应变率关系动态损伤本构模型。胡学龙等[20]以统一强度准则为屈服准则建立的动态本构模型不仅能描述岩石的硬化/软化行为，还可反映其应变率效应。针对煤岩，王登科等[21]根据岩石力学的强度理论和统计损伤理论建立了煤的强度型统计损伤本构模型，与现有元件型模型对比发现强度型模型同样能有效描述岩石动态力学性质，但强度型模型具有结构简单、参数少、物理意义清晰等优势。此外，冲击荷载下煤岩动态强度和破坏应变具有明显的应变率效应，而煤岩动态强度型损伤本构模型能较好反映应变率对应力-应变曲线的影响[22]。然而就目前的研究来看，针对煤岩这一特殊岩石虽有研究，但不同煤岩离散性特征明显，其变形本构必定存在差异，开展不同应变率下煤岩的强度本构关系研究仍具有重要意义。

因此，本文中利用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）试验系统，对四川省宜宾市芙蓉白皎煤矿煤岩展开全过程实时高速摄影监测的单轴冲击压缩试验，依托不同动态应变率下煤岩变形破坏的力学特性、破碎分维特征，深入探究煤岩的动态破坏特征，最终提出基于煤岩动态力学性质的强度型统计损伤本构模型，以期为煤矿安全、高效开采，煤岩动力灾害预测、防治，提供科学依据和工程指导。

1 试验概况

1.1 煤岩试样制备

本次试验选用宜宾芙蓉白皎煤矿2#煤层，埋深+350 m，富灰富硫无烟煤制样。依据国际岩石力学与岩石工程学会（ISRM）[23]推荐，将煤岩按长径比1∶1 制备 ∅ 50 mm×50 mm 的圆柱形煤岩试样27 个，保证煤岩试样打磨后两端面不平行度小于0.05 mm，两端面均垂直试样轴线，最大偏差度不超过0.25°。

1.2 试验装置

本次试验利用中南大学资源与安全工程学院的SHPB 动静组合加载试验系统，装置弹性杆为40Cr 合金材质，直径为50 mm，长度为2 m，密度为7 697 kg/m3，泊松比为0.28，弹性模量为240 GPa，弹性杆纵波波速为5 410 m/s。试验系统利用冲击气压进行控制，采用半正弦应力波加载，通过粘贴在入射杆和透射杆上的应变片采集脉冲信号，并将信号传入数据采集系统以获取试样的入射、反射和透射应变值。为减小试验过程中产生的摩擦效应，在试样和弹性杆的接触面上均匀涂抹凡士林。SHPB 试验装置如图1 所示。

1.3 试验数据

SHPB 试验测试技术满足应力传播一维假定和应力均匀性假定，本文单轴试验所得数据的有效性均已得到了验证[24]。根据数据采集系统收集的应变波数据，由下式确定煤岩试样的应力σ、应变ε 以及应变率 ε˙ ：

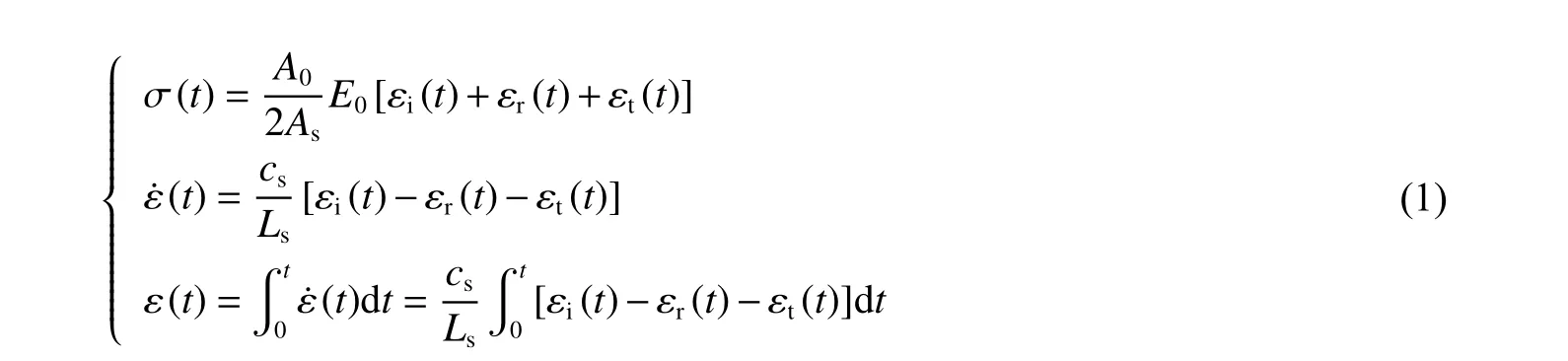
式中：A0为弹性杆横截面积，As为试样横截面积，E0为弹性杆弹性模量，cs为试样中弹性波波速，Ls为试样长度，εi(t)、εr(t)、εt(t)分别为测得的入射、反射、透射应变，t 为时间。

对27 个煤岩试样进行了9 组试验，每一组按同一气压进行了3 次平行试验，各煤岩试样的试验数据汇总见表1。表中，D 为煤岩试样的直径；Ls为煤岩试样的长度；ρ 为煤岩试样的密度；为平均应变率，由于试验系统设定的不同气压会产生不同的冲击速度，则不同的冲击速度对应不同的应变率；σd为动态抗压强度，本文中σd取应力-应变曲线的峰值应力；εm为应力峰值所对应的应变值；Ed为动态弹性模量，本文中Ed取应力-应变曲线中50%峰值应力处近似直线段的斜率。

煤岩作为一种离散性较大的岩石，为合理规避其自身缺陷影响并确保试验煤岩的一致性，本文分别对煤岩密度、弹性模量2 个参数进行离散性分析。表1 中分别计算了密度和弹性模量的变异系数，变异系数越大，离散度越大。根据GB/T23561.1—2009[25]，表1 中的变异系数均小于20%，满足试验要求。

表 1 煤岩基本物理力学参数Table 1 Basic physical and mechanical parameters of coal rock

2 煤岩冲击破坏力学性能分析

2.1 动态应力-应变曲线

图 2 煤岩动态应力-应变曲线Fig. 2 Dynamic stress-strain curves of coal rock

根据式(1)计算所得结果，每组气压下各选取一个煤岩试样绘制动态应力-应变曲线，如图2所示。从图2 中可看出，煤岩动态应力-应变曲线呈现明显的非线性特征。应力-应变曲线大致分为4 个阶段：Ⅰ为线弹性阶段，由于冲击加载过程时间短、冲击大，曲线没有明显的压密阶段，而是直接进入线弹性阶段；Ⅱ为塑性屈服阶段，此时弹性能不断积聚，致使煤岩内部原生裂纹迅速扩展、延伸并产生新裂纹；Ⅲ为峰值应力阶段，应力-应变曲线存在一段平台区域，这一现象与煤岩内部的裂隙闭合度相关，受到冲击荷载作用时煤岩内部裂隙重组并达到新的平衡状态，由于达到峰值应力时新的平衡状态还未被打破，应力-应变曲线就出现了平台阶段，文献[17]中也提到了这一阶段；Ⅳ为塑性软化阶段，此后煤岩承载能力下降，冲击煤岩破碎导致其力学性能劣化。对比不同应变率下的应力-应变曲线可以发现，煤岩具有较强的应变率相关性，随应变率升高，塑性屈服阶段明显变长，轴向变形量随之增大。

2.2 煤岩动态力学特征

2.2.1 动态抗压强度变化规律

图3 为不同应变率下煤岩抗压强度σd的变化规律。对比不同应变率下芙蓉白皎煤岩的抗压强度可以发现，准静态应变率下抗压强度在8.83～12.57 MPa 的范围内[26]，增长率为42.35%，而在动态应变率20～100 s-1范围，煤岩抗压强度从8.01 MPa 增至32.82 MPa，增长率约为310%。随应变率的升高，准静态和动态抗压强度整体上均呈现增大的趋势，且应变率越高抗压强度的增幅越大。当应变率低于50 s-1时，煤岩抗压强度较低，甚至和准静态抗压强度相近，而应变率高于50 s-1时，抗压强度显著增大。这是由于低应变率下煤岩未能完全呈现出其动态力学特性，因而强度处于较低的水平，但在高应变率下应变率变化对抗压强度的影响逐渐增强，这与文献[4]的试验结果相似。

2.2.2 动态弹性模量变化规律

煤岩动态弹性模量Ed与应变率的关系曲线如图4 所示。从图4 中可以看出，煤岩动态弹性模量集中在2～13 GPa。对处于不同应变率状态下的煤岩，其动态弹性模量具有一定的离散性，但随应变率的升高弹性模量总体上符合线性增长规律。弹性模量越高，煤岩变形刚度越强，则其抵抗变形破坏的能力也就越强。

图 3 不同应变率下的抗压强度Fig. 3 Compressive strengths under different strain rates

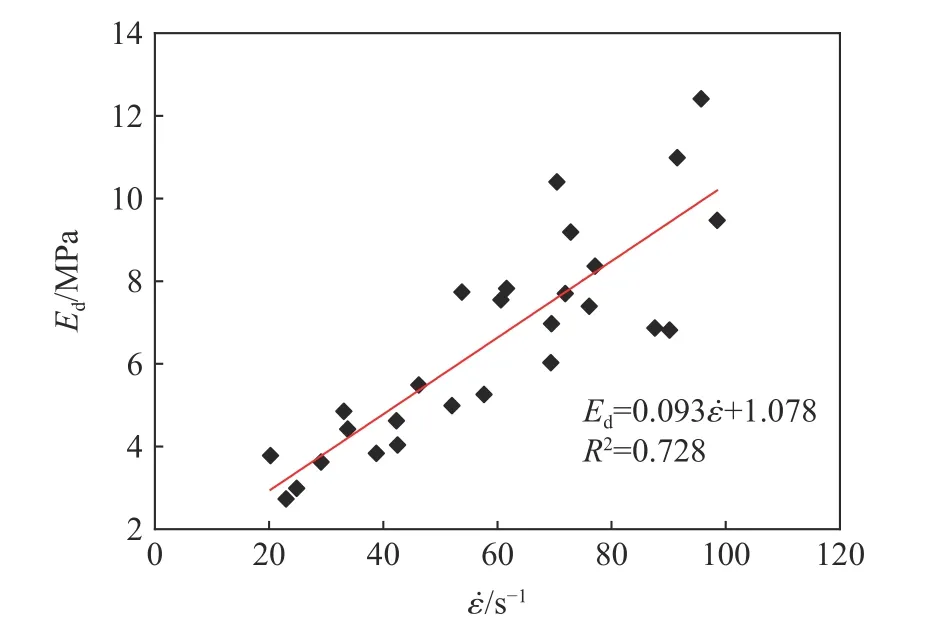
图 4 不同应变率下的弹性模量Fig. 4 Elastic modulii under different strain rates

2.3 煤岩动态变形破坏特征

煤岩的宏观破碎是煤岩在荷载等外部因素作用下，原始缺陷不断扩展、贯通，最终导致破碎的结果[27]。煤岩内部结构缺陷杂乱无章、随机分布，动态冲击压缩破坏形态形式多样，如拉裂、剪切、压碎、周边脱落等。不同应变率下煤岩的破碎特征如图5 所示。从图5 可以看出，单轴冲击压缩下，应变率较低时，如图5(a)所示，煤岩试样多由内部原生裂纹起裂，并沿平行于轴向应力的方向发生拉裂破坏。应变率较高时，如图5(g)～(i)所示，煤岩发生压碎破坏，且破坏过程中伴有周边脱落，最终试样被压碎为许多大小不一的块体。因此，随应变率升高，煤岩破碎程度越剧烈，小颗粒破碎块体越多。

为准确反映煤岩动态冲击压缩破坏全过程，试验过程中配置Photron 公司的FASTCAMSA1.1 高速数字式摄像机系统，分辨率为192×192，影像帧频为100 000 s-1，每10 μs 拍摄一张照片。选取2 个煤岩试样破坏全过程的高速摄影图片进行分析，如图6 所示。从图6 可以看出，煤岩破坏经历了由裂纹萌生、扩展到贯穿的过程。由图6(a)可以发现，69.36 s-1应变率下，煤岩试样承受冲击荷载作用约2 652 μs 时裂纹沿轴向起裂并向两端扩展，此时应力波已在岩样中来回传播了约19 次，2 812 μs 时试样上部开始出现碎块脱落，3 000 μs 后裂纹迅速贯通煤岩试样，发生劈裂破坏，产生很多尺度不一的破碎块体。由图6(b)可以发现，91.51 s-1应变率下，煤岩试样承受冲击荷载作用约1 682 μs 时试样表面出现多条横向裂纹，此时应力波已在岩样中来回传播了约18 次，1 982 μs 时裂纹贯通试样且碎块脱离弹性杆，2 000 μs 后试样迅速被压碎，具有明显的剪胀特征。由此可以发现，随应变率升高，应力波在煤岩试样中传播的次数越少，破坏时间越短，且煤岩破坏形态大多由轴向劈裂破坏向压碎破坏过渡。

图 5 不同应变率下煤岩的动态破碎特征Fig. 5 Dynamic fracture characteristics of coal rock at dfferent strain rates

图 6 两个典型煤岩试样动态破坏过程的高速摄影图片Fig. 6 High-speed photographies for the dynamic fracturing process of two typical coal rock specimens

3 煤岩破碎特征分析

如前所述，单轴冲击压缩下，煤岩破裂为许多大小不一的碎块，收集试验后的煤岩碎块，采用0.25、0.50、1.00、5.00、10.00、20.00、40.00、50.00 mm 的标准筛对煤岩的破碎颗粒进行筛分，发现碎块具有明显的自相似性，能够较好地利用分形理论进行讨论。分形理论20 世纪70 年代由Mandelbrot 创立[28]，1991 年由谢和平等[28]首先将其与岩石力学结合，开创了岩石分形领域新篇章。破坏后的煤岩碎块块度具有分形特性，究其原因在于煤岩的几何特征和力学、物理量演化的数字特征都表现出良好的自相似性[9]。

采用质量-尺寸关系计算分形维数Db[9]，其计算公式如下：

式中：r 为标准筛尺寸，M(r)为直径小于r 的块体累积质量，MT为试验煤岩总质量，α 为煤岩破碎块体的质量-尺寸分布指数，在直角坐标系中以lg[M(r)/MT]为纵坐标，lg r 为横坐标绘制曲线并进行线性拟合，所得直线的斜率即为α。

同时，筛分后取各粒度含量的加权平均值作为煤岩破碎平均块度dm，其计算公式如下[29]：

式中：di为每一粒级煤样的尺寸，ri为每一粒级破碎煤岩块体质量累积百分率。

根据表2，得到煤岩破碎平均块度、分形维数和应变率的关系如图7 所示。从图7 可以发现，单轴冲击压缩状态下，煤岩试样破碎平均块度集中在30～40 mm，且随应变率升高，煤岩破碎平均块度总体呈下降的趋势。当应变率为24.84 s-1时，冲击压缩过程中煤岩试样被压缩程度低，只有小块碎屑脱落，平均块度较大，但应变率越高煤岩试样初始阶段获得的能量越多，导致其破碎程度增强，破碎块度随之减小。单轴冲击压缩状态下，煤岩破碎块度分维值集中在1.9～2.2，说明煤岩试样破碎块度基本处于小尺度区间内。在40～80 s-1应变率范围内，随应变率升高，分形维数增大，表明大尺度煤岩碎块占总质量的比例减少，煤岩破碎程度随之增强，破碎块度越来越小。综上可知，煤岩破碎块度分维值可以反映煤岩在不同应变率下的破碎程度，因此分形维数在煤矿高效开采中具有指导性意义。

表 2 不同应变率下煤岩的破碎特征Table 2 Fragmentation characteristics of coal rock at different strain rates

图 7 煤岩破碎平均块度、分形维数与应变率的关系Fig. 7 Average fragmentation and fractal dimension of coal rock at different strain rates

4 煤岩动态损伤本构模型

4.1 损伤变量的定义

煤岩作为一种典型的非均质材料，内含大量随机分布的微裂隙、孔洞等缺陷，假设煤岩由大量微元体组成，其尺寸在空间意义上足够大能包含大量微缺陷，但在力学意义上又充分小可将其视为一个质点。微元体具有以下性质：（1）煤岩在宏观上表现为各向同性，即各向同性损伤体；（2）煤岩破坏前服从胡克定律，破坏后不具备承载能力；（3）各微元体强度服从Weibull 分布。其概率密度函数表达式为：

式中：F 为微元体强度的分布变量，F0、m 为Weibull 分布参数，反映了煤岩材料的力学性质。

当煤岩受冲击荷载作用时，微元体将逐渐发生破坏，可引入统计损伤变量D 来反映这一过程，在某一荷载的作用下，D 可表示为：

式中：N 为总微元数，Nf为已破坏的微元数，当加载到某一荷载水平F 时：

将式（5）、（7）代入式（6），可得损伤变量D 的表达式：

4.2 微元体强度

根据式（8）可知，损伤变量D 受到微元强度F 的影响，而微元强度与岩石所处的应力状态有关。为了体现复杂应力状态对煤岩的影响，认为微元体的破坏准则符合Drucker-Prager (D-P)破坏准则。基于D-P 破坏准则的岩石微元强度为[21]：

式中：α 为微元体的强度参数，φ 为岩石的内摩擦角，本文所选用的芙蓉白皎煤岩的内摩擦角为22.95°[29]，则α 的值为0.126 8，I1为应力张量的第一不变量，J2为应力偏量的第二不变量。

将式(10)代入式(9)，本文中煤岩处于单轴状态，因此σ2=σ3=0，ε1=ε，则微元体强度的表达式为：

4.3 本构模型的建立与修正

利用应变等效假设，获得冲击荷载作用下单轴煤岩的强度型统计损伤本构模型的表达式为：

由式(12)可知，建立本构模型的关键在于确定两个未知参数F0和m。考虑到单轴冲击试验中能够较易获得应力-应变曲线的峰值应力及其对应的应变，因此本文采用极值法来确定参数F0和m。由于多元函数在极值点（εm, σmax）处导数为0，将式(11)、(12)两边同时对ε 求导并化简得：

式中：σmax、εm、E 的取值见表1，最终本构模型参数计算结果见表3。

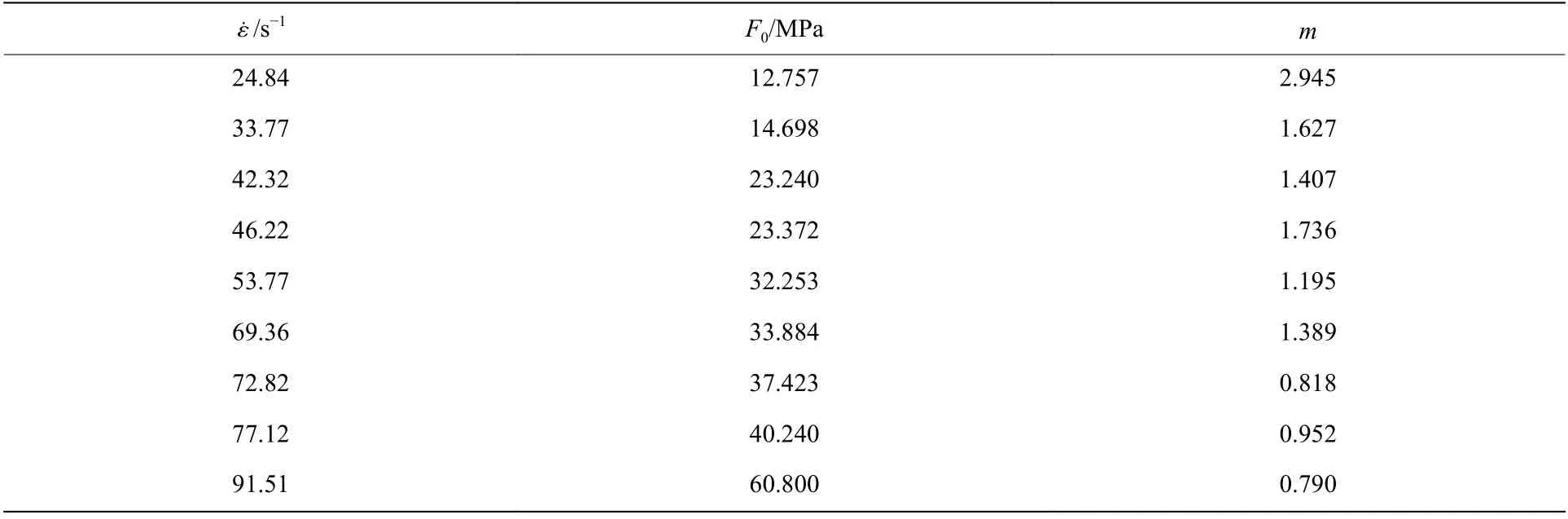
表 3 本构模型参数计算结果Table 3 Computational results of constitutive model parameters

由表3 可以发现，参数F0、m 与应变率存在一定的相关关系，随应变率升高，F0越来越大，而m 大致呈现下降的趋势。分别建立F0、m 和应变率的关系，可以有效地对煤岩的损伤统计本构模型进行修正。分别以F0与m 为纵坐标，应变率为横坐标绘制散点图并进行非线性拟合，如图8、9 所示。

图 8 参数F0 随应变率的变化关系Fig. 8 Variation of parameter F0 with strain rate

图 9 参数m 随应变率的变化关系Fig. 9 Variation of parameter m with strain rate

经拟合可知，F0、m 和应变率的关系如下：

其拟合相关系数分别为0.95 和0.89。将式(15)、(16)代入(12)可得到修正后不同应变率下煤岩的强度型统计损伤本构方程：

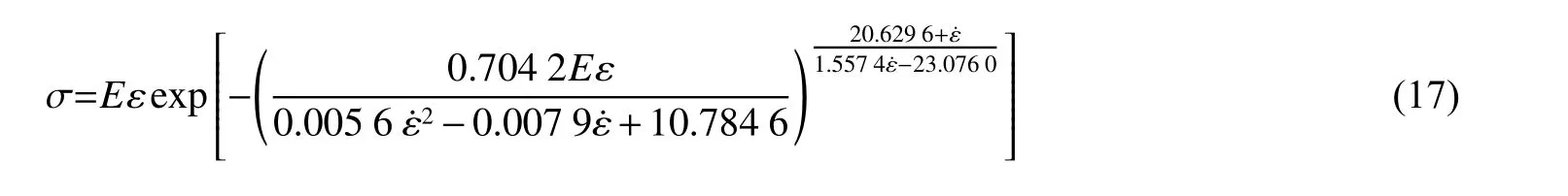
4.4 本构模型的验证

利用修正后的本构模型，由式(17)计算得到不同应变率下煤岩动态应力-应变理论曲线，并与试验曲线进行对比，如图10 所示。

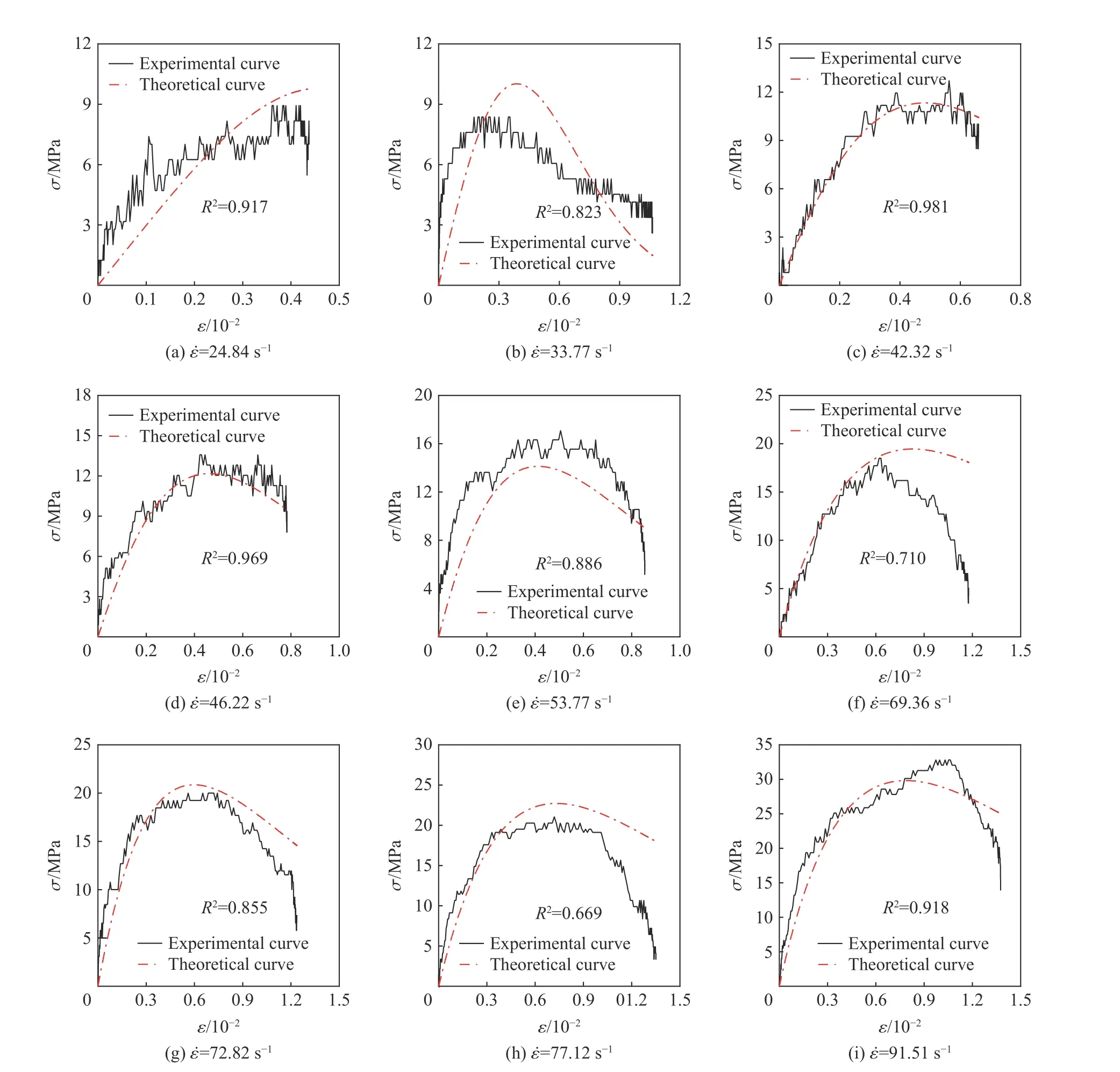
图 10 不同应变率下煤岩试验和理论应力-应变曲线Fig. 10 Comparison between experimental and theoretical stress-strain curves of coal rock under different strain rates

由模型验证结果可知，在20～100 s-1应变率范围内，理论曲线和试验曲线基本具有较好的一致性，受Weibull 分布参数F0和m 的影响，理论曲线的合理修正使得其能够较好地反映煤岩抗压强度、弹性模量随应变率升高而增加的动态力学特性，具有较强的率效应反馈，能够更好地服务于实际工程。当然，本文所建模型未能完全对应煤岩动态应力-应变曲线各加载阶段的变化过程，存在一定的局限性，且模型参数确定、弹性模量选择所产生的误差均需要在以后的研究中进一步改进。

5 结 论

针对芙蓉白皎煤岩单轴冲击压缩试验20～100 s-1动态应变率范围下的动态破坏特征及本构关系进行分析，得到以下结论。

（1）煤岩动态应力-应变曲线具有明显的非线性特征，可分为线弹性、塑性屈服、峰值应力、塑性软化4 个阶段。随着应变率升高，试验煤岩的动态抗压强度从8.01 MPa 提高到32.82 MPa，动态弹性模量从2 GPa 左右增长到约13 GPa，煤岩刚度显著增强。其动态破坏形态由低应变率下的轴向劈裂破坏向高应变率下的压碎破坏过渡。

（2）不同动态应变率范围下，试验煤岩的宏观破坏碎块分形特性明显，煤岩破碎平均块度为30～40 mm，破碎块度分维值为1.9～2.2。随应变率升高，分形维数增大，平均破碎块度呈减小的趋势，表明大尺度碎块占煤岩碎块总质量的比例逐渐减小，煤岩破碎程度增大。

（3）基于试验煤岩微元强度服从Weibull 统计分布、微元体破坏符合D-P 破坏准则的假设，对参数F0、m 进行修正，建立了不同应变率下煤岩的动态强度型统计损伤本构模型。该模型能够充分反映煤岩应力、应变和应变率的关系，其有效性、合理性得到较好的验证。