Entropy-KNN算法在岩性识别中的应用研究

2021-05-27王林王禹杰合肥市测绘设计研究院安徽合肥230061

安徽建筑 2021年5期

王林，王禹杰（合肥市测绘设计研究院，安徽合肥 230061）

1 引言

岩石识别是地学研究中的一项重要工作，其结果有助于储层评价、油藏描述以及实时钻井监控等方面。综合考虑时效性、安全性以及成本，多采用测井资料解释处理获取岩性信息。近年来，随着计算机技术的发展，许多学者深度拓展利用测井资料识别岩性的方法，由传统的岩心岩屑和薄片识别法、交会图法延展出对应分析法、K—邻近法、判别分析、神经网络、支持向量机等方法，但每种方法都存在一定的不足。利用岩心、岩屑和薄片资料，识别碳酸盐岩受主观因素影响较大，且识别效果存在片面性；交会图法操作简单，但仅限于线性可分的分类问题，对于复杂岩性的分类问题，识别精度较低；K-邻近法按照欧氏距离单一标准搜索待判岩的K邻近，分类标准过于单一。且上述分类标准均采用岩石测井参数，并未与岩石力学参数结合。

辽西隧道三号斜井正洞至出口区间穿越断层破碎带，岩体破碎，属极I级高风险隧道。测井参数收集危险性较高，且分布模糊，为此处的岩性识别带来了困难。利用隧道开挖前收集的岩石力学参数，提出基于岩石力学参数信息熵的Entropy-KNN识别岩性。该算法寻找训练样本与测试样本的相同岩石力学参数，计算其平均信息熵，以此作为度量两个数据集接近程度的距离指标，选取K个与测试样本距离最近的训练实例，最终综合考虑训练实例中各类实例的个数及平均距离，依据待测样本属于各类的可信度，准确识别岩石类型，整体上提高了分类的准确性。

2 基于属性值信息熵的KNN分类模型

K——邻近算法，又叫KNN算法，是数据挖掘十大算法之一，核心思想是对于未知的测试集，按照定义的距离，选取样本集中距离它最近的K个实例参照，判断K个实例中样本类别，按少数服从多数的投票法则，判断未知实例所属离别。

对于训练集中类别交叉、类别重叠情况，传统KNN算法存在以下不足。当训练集中类别分布不均匀，某个类别样本容量大，其余类别样本容量小时，新输入的实例容易受最近的“邻近样本”主导，被归为大样本类别，事实上，可能该实例并未接近目标样本。为此引入距离加权—KNN算法，根据输入实例与K邻近样本的距离加权，考虑各距离权重，分析实例类别。但当各类邻近样本个数、平均距离相同时，该算法的分类输出解释性较弱，类别评分不规则，准确度无法保证。上述两种算法弊端在于样本间距离定义过于简单，未考虑属性值对类别判断的影响。Entropy—KNN定义距离为样本间相同属性的平均信息熵，基于此距离判断岩石类别。

2.1 方法原理说明

信息熵表示对信息不确定性的度量。Entropy—KNN基于信息熵理论产生，涉及到的概念包括属性值信息熵、相似度函数和类可信度指标。利用属性值信息熵判断该属性值对类别的决定作用大小，如果属性值信息熵越大，该属性值对类别判断作用越小。相似度函数用来定义点与点间的相似度，当样本间相同属性值信息熵小的属性值越多，相似度函数值相应越小，两个样本的相似程度越高。根据属性值信息熵和相似度函数，计算类的可信度指标，以此作为最终类别的评价指标，具体详细定义说明如下。

2.1.1 属性值信息熵

属性值信息熵表示属性值对类别中的重要性，某个样本的属性值信息熵越大，说明该样本类别确定越模糊；反之，如果某个样本的属性值信息熵为0，依据该属性值能够完全确定样本类别。

假设数据集为D，该数据集系统共有d1，d2，......dn个类别，若属性V具有i个不同值{v1，v2，......vi}，属性值 vi在 D中出现的次数记作|vi|，属于第j类的实例个数记为|vij|，则属性值vi的信息熵为：

2.1.2 相似度函数

相似度函数在聚类、领域搜索中应用非常广泛。在岩性识别中，定义样本间相同属性值的平均信息熵为相似度函数，度量样本点间差异性大小。两个样本的相同属性值中信息熵大的属性值越多，平均信息熵越大，这两个样本的相似程度越低。

设M,N为任意两个样本，在M，N中相同属性值为 v1，v2，......vn，M,N 的相似度函数为：

2.1.3 类可信度指标

Entropy-KNN算法以各类别的邻近样本点个数及未知样本与相似样本间的类别平均距离作为类可信度指标，弥补了传统KNN算法只考虑不同类别的近邻点个数，距离加权-KNN算法只考虑不同类别的近邻样本点个数的平均距离的不足。

设数据集S中di代表类别，M为待测样本，Xi为近邻中属于di类的样本，N为近邻样本总数，Ni为近邻样本属于di类的样本个数。称T（di，M）为M对Ci的类可信度，计算公式如下：

3 岩性及力学参数特征

3.1 研究区概况

本实验所采用的数据集来自辽西隧道三号斜井正洞至出口区间的隧道超前地质预报数据，对测井资料的分析得到，研究区岩石的类型主要为安山岩、玄武岩、花岗岩、砾岩和闪长岩这5种岩性。由于岩石特征复杂多样，这为岩石的解释和识别工作带来了巨大挑战，因此，该地区的岩性分类解释工作至关重要。

3.2 岩石力学参数特征

本实验基于辽西隧道超前地质预报获得的地震波数据，经过滤波处理，抽取1000组岩石力学参数数据，通过数据分析得出以下五种特征，对于分类具有重要意义，分别是：纵波波速、横波波速、弹性模量、泊松比、密度。

对不同岩性力学参数的均值进行统计（表1），对不同属性的均值方差进行统计（表2）。结果显示：密度、泊松比和横波波速这三个特征变化范围和幅度小，弹性模量变化范围和幅度大。闪长岩的平均弹性模量为109.10GPa，远低于总体平均值65.35GPa，纵波波速为6.08km/s，较总体平均值5.01km/s高很多。相反地，砾岩的纵波波速2.9km/s远低于总体均值，其弹性模量也低于总体平均值。分析可知，纵波波速和弹性模量对砾岩和闪长岩的敏感性差异很大。同时，安山岩的纵波波速和横波波速这两个岩性变化范围非常小，值比较稳定，对玄武岩恰恰相反，纵波波速相对较大。以上分析说明，不同岩性力学参数的敏感度不同，故不同岩性力学参数敏感度权重对分类具有重要意义。

不同岩性力学参数的均值统计表表1

不同属性的均值方差统计表表2

二维交会图更直观地反映了数据在二维空间的分布情况，以密度—横波波速，弹性模量—横波波速为例（图1），部分岩性空间分布存在大量交叉重叠，说明各力学参数具有很大的模糊度，使该研究区样本岩性的识别工作较为困难，样本可信度的判定对岩性识别工作具有显著意义。

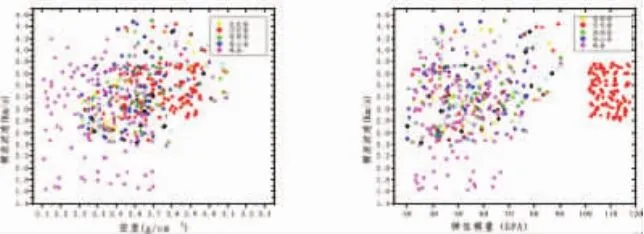
图1 原始力学参数交会图

4 实验

4.1 实验数据及评价指标

所有的实验在辽西隧道三号斜井正洞至出口区间的隧道超前地质预报数据集上进行，选取6000组记录作为实验集。采用3—折交叉验证法评价分类精度。数据集被随机分成三个子集，每个子集大小相等，每次随机抽选2000组数据作为测试集，剩余数据作为训练集。Entropy-KNN算法在每个数据集上循环运行若干次，取实验期望作为数据集的分类准确率结果。实验中，该算法运行20次，采用分类正确率作为分类精度评价指标，与传统KNN算法和距离加权KNN算法交叉比较。