履带起重机行走部件尺寸匹配方法研究与仿真

张瑞武 王昌磊 滕儒民 李自军 王 欣

1大连理工大学机械工程学院 大连 116000 2湖南中联重科履带起重机股份有限公司 长沙 410000

0 引言

履带起重机用于物料运输、装卸和安装等作业，具有起重能力强、接地比压小、转弯半径小、爬坡能力大、不需支腿、带载行走、作业稳定性好等特点。履带行走的平稳性对减少运动冲击、载荷冲击具有至关重要的影响。如果履带起重机驱动轮与履带板之间啮合不好，会造成啃齿及整机抖动现象，影响操作者的舒适性，也不利于起重机的工作性能，故对两者尺寸的运动匹配性研究十分必要。

业界学者在履带行走方面开展了充分研究。诸文农等[1]推导了履带板与驱动轮尺寸的计算方式，根据履带式机械自重确定履带板节距，结合驱动轮齿数，获取驱动轮节圆尺寸。鲍晓杰[3]提出通过调节驱动轮与履带板间的啮合尺寸来解决啃齿的方法。崔雪斌[4]通过动力学分析得出通过减小履带链节距，减小链环不均匀系数使履带行走机构获得更好平稳性的方法。卢进军[5]利用RecurDyn软件建立履带车辆多体动力学模型，为履带车辆转向性能的研究与高速转向的正确操作提供指导。

这些研究在工程机械应用广泛，为各类履带车辆底盘设计以及相关优化提供理论基础。目前，更多是基于理想尺寸下的研究，而实际尺寸的公差对行走机构的平稳性影响至关重要。为此，本文以履带起重机行走机构为例，根据驱动轮与履带板的理想啮合条件，分析两者的公差配合，提出避免啃齿的尺寸条件，通过不同算例对比分析以及仿真验证计算方法。

1 履带行走机构工作原理与理想啮合条件

履带起重机行走机构的工作原理是由发动机提供动力，驱动行走马达旋转，带动驱动轮转动，通过驱动轮与履带板的槽齿啮合，最终将驱动轮的旋转运动转为履带板在地面的直线运动。

在理想情况下，履带板与驱动轮啮合时可看作履带板围成的多边形内切于驱动轮的直径，如图1所示。根据圆与多边形的几何关系，可得履带板节距与驱动轮直径的关系为

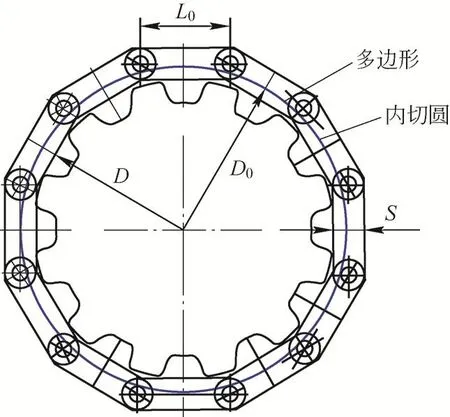
图1 履带板节距与驱动轮直径关系（理想情况）

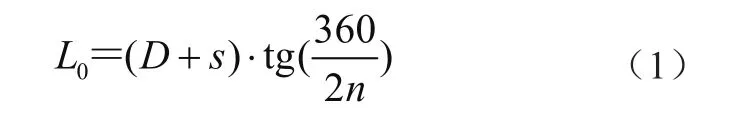
式中：L0为履带板节距，D为驱动轮直径，s为履带板厚度，n为驱动轮槽的数量。

理论上希望驱动轮与履带板如同精密传动一般完美啮合，即在履带板张紧情况下，驱动轮接近一半的槽与履带板齿处于啮合状态。这就需要履带板的轴孔配合公差为零，履带板节距与驱动轮直径关系恰好为理想状态。在实际情况下，履带板与驱动轮都是铸件，不可避免地存在铸造误差或铸造后的加工误差，难于实现多对齿槽啮合，往往只有一对齿槽啮合。尺寸误差的进一步加大，会出现啃齿即齿槽啮合和脱开不顺畅现象，同时会伴随有履带的抖动现象以及履带板在地面处的堆积情况。因此，公称尺寸下的履带板与驱动轮不啃齿，并不能保证考虑公差时也不啃齿，故需研究履带板与驱动轮两者不啃齿条件下的公差配合关系。

图2、图3分别为履带行走时的啃齿与履带板堆积的模拟。这些现象不仅与履带板与驱动轮的尺寸误差有关，还与各履带板之间的轴孔公差有关。履带板轴孔公差过大时，会导致履带板脱离啮合后的不顺畅，从而引起履带板在地面处的堆积。

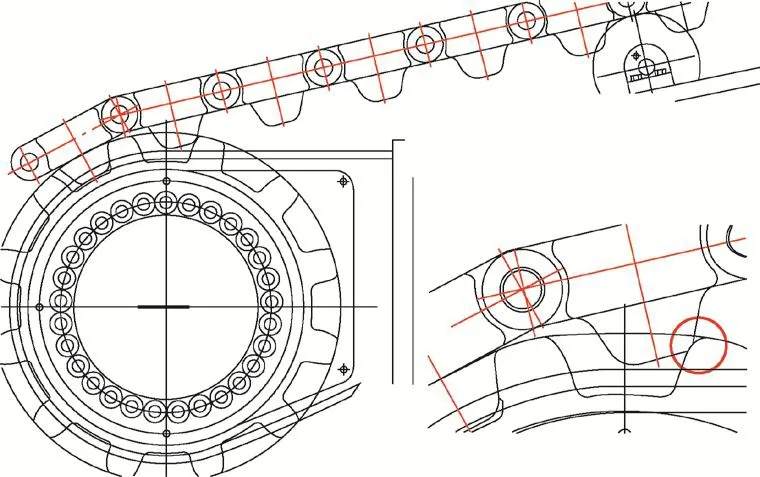
图2 履带板啃齿模拟

图3 履带板堆积模拟

由上述分析可知，为了减少啃齿现象，实现履带板与驱动轮的顺畅啮合，需要考虑的尺寸公差有：履带板节距公差、履带板孔公差、履带板轴公差、驱动轮直径公差等。

2 已知驱动轮直径公差时的履带板节距公差分析

在不考虑尺寸公差的理想啮合状态下，若驱动轮转动方向如图4所示，履带板齿后面和驱动轮槽后面应刚好接触（图4中位置3）。为了在此接触面上不发生啃齿，应使履带板实际节距L≤L0，L0为理想状态下的履带板节距。

图4 履带板齿与驱动轮槽的啮合示意

如果履带板实际节距过小，会引起履带板齿前面和驱动轮槽前面的接触（图4中位置4），导致前面啃齿。考虑履带板齿与驱动轮槽存在间隙，表示为p-b，（见图5），当啮合在最不利位置时（由于尺寸误差，通常只有一对齿槽啮合），即在驱动轮下方接近地面处（图4中位置5），此时齿和槽后面完全接触，由于履带板节距小，存在齿槽间的误差，并逐渐累积到驱动轮上方履带板齿要进入槽的位置，则在该位置处不发生齿和槽前面（图4中位置4）接触的条件是

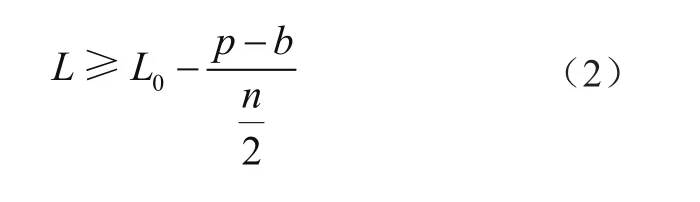
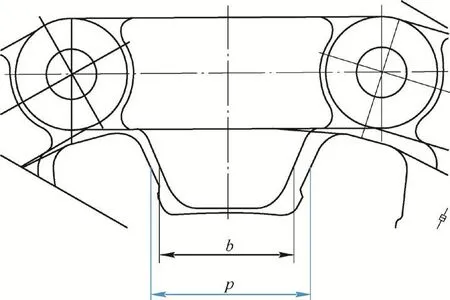
图5 履带板齿宽和驱动轮槽宽

由此，为不发生履带板齿进入驱动轮槽时的前后啃齿现象，根据驱动轮直径确定的履带板节距公差范围为

驱动轮直径也有公差范围，可根据式（3）分别计算出驱动轮最小公差直径和最大公差直径时的履带板节距公差范围，然后取这两种情况下履带板节距公差范围的重叠范围，作为履带板实际节距最终的公差范围为

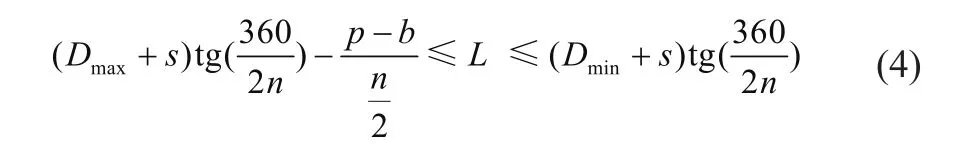
履带板实际节距与履带板轴孔公差和履带板两孔中心间距有关，如图6所示，可根据式（5）确定单个轴孔公差范围之和Δe，其中，ΔL为履带板两孔心间距正公差，可表示为

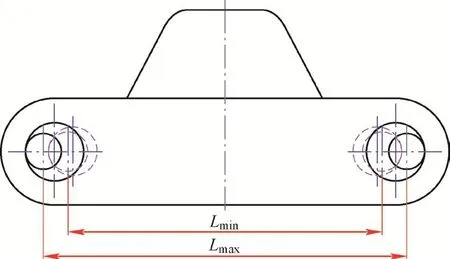
图6 履带板的实际节距范围[Lmin,Lmax]

如果已知履带板节距公差，可根据啮合条件推得驱动直径的公差范围。由式（1）可得理想啮合条件下的驱动轮直径，即

式中：D0为驱动轮直径。

为了不出现齿与槽的后面啃齿，应使驱动轮直径D≥D0。考虑履带板节距的公差，驱动轮直径应大于最大公差下的履带板节距推得的驱动轮直径，即

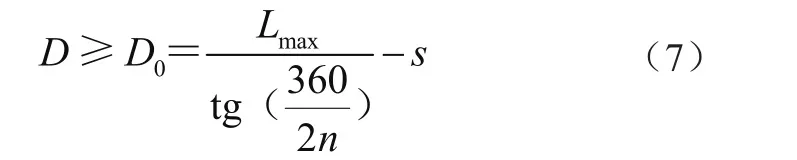
由于齿和槽间隙（p-b）较大，出现齿和槽的前面啃齿几率较低，但如果设计不当，也要考虑驱动轮最小直径的要求，见式（8）。由此联立式（7）和式（8）可得到驱动直径的公差范围。

3 算例分析

以实际运动出现啃齿差的某型号履带起重机产品为例，根据履带板节距公差来推导驱动轮直径公差。已知履带板节距为250±1 mm，履带板孔径为φ410+1.5mm，销轴直径为φ40 mm，可推得履带板实际节距公差范围Lmin＝250 mm，Lmax＝253.5 mm，驱动轮上有12个槽，即n＝12，根据啮合尺寸，图示5中的p＝136 mm，b＝111 mm，履带板厚度s＝90 mm。代入式（7）、式（8）得

给定的驱动轮直径为φ850±2 mm，没有在本计算范围内，故发生了啃齿现象。根据计算结果，将驱动轮直径改为，经实际运行试验，未发生啃齿现象。

4 运动仿真分析

根据算例中的某型号产品下车行走机构（见图7a）在Recurdyn软件中建立运动仿真模型（见图7b），代入改进前后的驱动轮直径尺寸，其他尺寸保持不变，模拟发动机转速为1 700 r/min的行走后退工况，运行速度在0.46 m/s ，可得改进前后驱动轮中心处的竖直方向加速度曲线，如图8所示。由此可知，改进前的加速度波动幅度较大，在±1 m/s2之间，这是由啃齿引起的。改进后的加速度在±0.2 m/s2之间，波动幅值明显减小，仿真中没有啃齿现象，履带板齿能顺利落在驱动轮槽内。由此通过仿真，再次验证了前面计算分析的合理性。

图7 产品行走机构模型

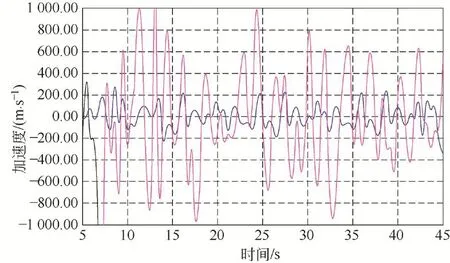
图8 驱动轮加速度曲线

5 结论

根据履带行走的工作原理，分析理想尺寸下的履带板与驱动轮的啮合条件。根据不啃齿的条件，确定两者公差带之间的关系，通过实际算例及运动仿真，表明本文提出的履带板与驱动轮的尺寸匹配方法的合理性，为相关的尺寸设计提供了理论基础。